排除干扰聚焦图形，识别模型平移转化——以一道最小值把关题的讲评为例

☉江苏常熟市第一中学 谢 燕

排除干扰聚焦图形，识别模型平移转化
——以一道最小值把关题的讲评为例

☉江苏常熟市第一中学 谢 燕

最值问题一直是初中数学各级考题中的热点设问角度，各种最值模型纷繁复杂，辨识模型需要较高的识别、洞察问题结构的能力.比如所谓“将军饮马”模型就有很多变式，其中一种融入平移的“将军饮马”模型显得更加复杂.在最近的中考模考卷中，我们又在某地区的模考卷的最后一题最后一问中发现了这种设问，而安排学生训练时，得分率太低，于是笔者搜集之前一些地区考卷中曾出现过的同类问题，构思了一节主题复习课，取得了较好的复习效果.本文先概述这节课的教学流程，并跟进解读教学立意，供研讨.

一、模考题讲评课复习流程

教学环节（一） 考题呈现，“遇上”难题.

考题1：如图1，平面直角坐标系xOy中，抛物线y=ax2（a≠0）经过点B（-2，4）.

（1）求a的值.

（2）作Rt△OAB，使∠BOA= 90°，且OB=2OA，求点A的坐标.

（3）在（2）的条件下，过点A作直线AC⊥x轴于点C，交抛物线y=ax2（a≠0）于点D，将该抛物线向左或向右平移t（t＞0）个单位长度，记平移后点D的对应点为D′，点B的对应点为B′.当CD′+OB′的值最小时，求出t的值和平移后相应的抛物线解析式.

思路突破：（1）比较基础，这里略去过程，直接给出答案a=1.

（2）需要分两种情况讨论.

如图2，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N.

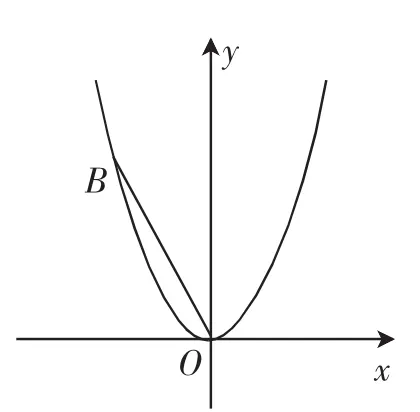
图1

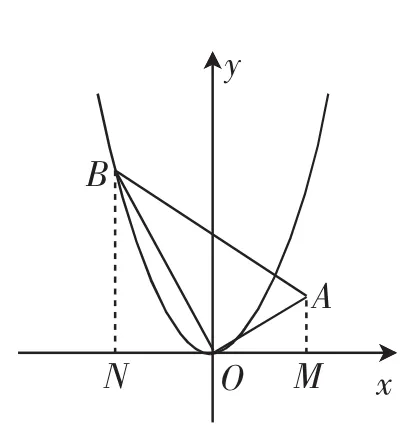
图2

图3

如图3，过点A作AM⊥y轴于点M，过点B作BN⊥y轴于点N.

类似地，可得OM=1，MA=2，即此时A点的坐标为（-2，-1）.

综上所述，A点的坐标为（2，1）或（-2，-1）.

现在就来到了难题第（3）问，由于在上一问中点A有两处位置，所以这一问也需要分类讨论，让我们先挑一个简单的突破思路.当A（-2，-1）时，构造图4分析，容易发现此时点D与点B重合，待求CD′+OB′的值最小，只需要取O关于直线y=4的对称点O′，连接CO′交直线y=4于B′，则该点为满足题意的点B′、D′，容易确认此时BB′=1，所以t=1，抛物线的解析式为y=（x-1）2.

图4

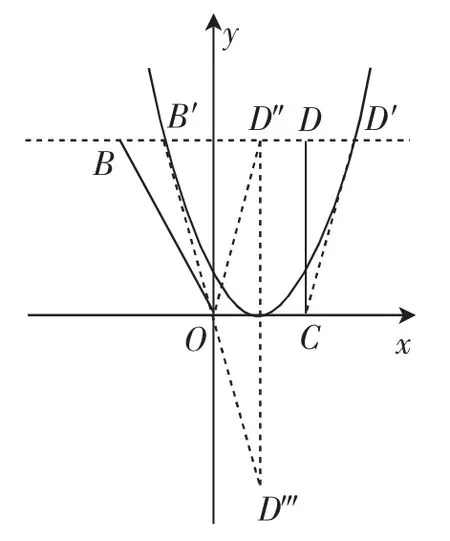
图5

再来思考点A（2，1）的情况，构造图5分析（先要想清抛物线如果向左平移，则待分析的CD′+OB′的值会越来越大，故舍去向左平移的讨论）.设平移后的抛物线解析式为y=（x-t）2，则B′、D′的坐标为B′（t-2，4）、D′（t+2，4），将点D′向左平移2个单位（这个平移长度对应着线段OC的长）得到D″，现在的问题就转化为前面的将军饮马模型了，只要取D″关于x轴的对称点D苁，连接B′D苁，当B′D苁恰过原点时，符合要求.接下来就用含t的式子表示B′D苁的解析式，再把（0，0）代入解析式，就可确定t=1.问题获得解决.

值得提醒学生的是，以上两种不同的构造与思考，其答案却是一样的.

教学环节（二） 巩固模型，加深理解.

考题2：如图6，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.

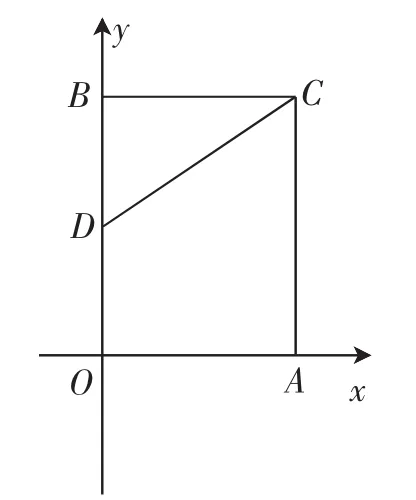
图6

图7

预设讲解：如图7，作点D关于x轴的对称点D′，在CB边上截取CG=2，连接D′G与x轴交于点E，在EA上截取.

由GC∥EF，GC=EF，易得平行四边形GEFC，有GE= CF.又DC、EF的长为定值，此时得到的点E、F使四边形CDEF的周长最小.由OE∥BC，可得Rt△D′OE∽Rt△D′BG，则.所以所以.即点E的坐标为点F的坐标为

回顾反思：轴对称最值模式需要经历平移变换（EF→CG）后获得GE+DE最短.

教学环节（三） 同类再练，学情反馈.

考题3：如图8，已知点A（-4，8）和点B（2，n）在抛物线y=ax2上.平移抛物线y=ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C（-2，0）和点D（-4，0）是x轴上的两个定点.当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由.

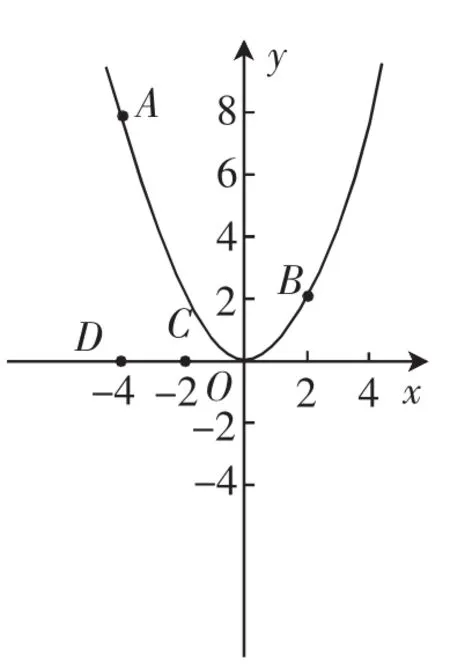
图8

设抛物线向左平移了b个单位，则点A′和点B′的坐标分别为A′（-4-b，8）和B′（2-b，2）.因为CD=2，因此将点B′向左平移2个单位得B″（-b，2）.要使A′D+CB′最短，只要使A′D+DB″最短.点A′关于x轴的对称点的坐标为A″（-4-b，-8），于是，可以求出直线A″B″的解析式为2.要使A′D+DB″最短，点D应在直线A″B″上.将点D（-4，0）代入直线A″B″的解析式，解得.故将抛物线向左平移时，存在某个位置，使四边形A′B′CD的周长最短，此时抛物线的函数解析式为

图9

二、教学思考

习题课是一首老歌，然而在各级教研活动中对习题课的研究并不多见，究其原因往往是觉得习题课缺少主线，一道习题接着一道习题讲评，品味不高，有浓浓的应试味道，如果我们能把具有相同结构的习题归类到一起，研发同类问题的专题复习课，则往往能让习题课也上出新意、上出深度.以下就围绕相关话题进一步阐释我们的思考.

1.教师要善于归类积累经典模型及其变式.

由于现今网络搜题的便捷，使得很多较难题能在一些网站、数学教师研究群里快速传播，进而出现在各类试卷中，如果教师不注意收集、积累这些常见图形及其性质，在教学中不进行必要的讲解与训练，在一些考试中学生往往面对这些新题型束手无策.而对这类较难题，首先需要教师本人善于归类积累经典模型，收集存档，以便在相关试卷中出现时，能第一时间在“手头”或电脑中查阅、比对，使得大量的同类变式题能在较短时间内被查找出为，为进一步备课、选题提供必要的同类题资料.

2.试卷讲课上较难题可引导学生识别模式.

每份中考复习模考卷中都有两三道把关题，这些把关题也是试卷讲评中的重点与难点，如果轻描淡写地核对答案式讲评，则讲评效果并不理想.怎样让学生通过这些较难试题的讲评能达到学活、学透、学深，是值得我们深入思考的.我们认为，像上文中的课例一样，不只是针对难题进行思路突破，而且在讲解之后，还要给出同类跟进，变式再练，让学生在“多解归一”中加深对模式的理解.

3.注意同类跟进变式再练追求更好的效益.

对于一些较难题的讲评或订正，很多学生貌似听懂了，但是再遇到这些题目时往往不能准确解答，为了有效应对这种“遗忘现象”（可能不能称之为遗忘，应该是学生的理解还不够深刻），根据我们的教学经验，在这些较难试题讲评之后，可以开展变式再练、同类链接，让学生在结构相同或解法思路相近的同类试题训练之后加深对这类问题的深刻理解，追求更好的教学效益.

三、写在后面

这类考题在本质上是几何最值模型“嵌入”抛物线背景，基本不涉及函数背景，所以上文中的考题2——一道几何矩形背景题也是考查这种最值模型，“嵌入”所谓函数图像只是为了干扰、影响学生的思路，如果受到函数图像等无关线条的干扰，不能聚焦图形、锁定目标，则往往不得其门.在这个意义上说，就命题来说，函数图像为背景“嵌入”这种几何最值模型并不是值得提倡的命题方向；就教学来说，引导学生善于排除干扰，聚焦目标是应试解题的必备解题技能.

1.王成.同类链接促进感悟，模考讲评提升效益——以一次模考题的链接讲评为例［J］.中学数学（下），2017（2）.

2.沈丽婧.聚焦微专题：中考二轮复习的实践与思考——以一组“关联试题”复习为例［J］.中学数学（下），2017（3）.

3.秦怡.回到概念，让解题念头“自然生成”——从一道几何难题的思路突破说起［J］.中学数学（下），2017（2）.

4.徐燕君.一道“伪坐标题”的命题商榷与变式改编［J］.中学数学（下），2017（1）.