扩张与因袭：问题情境的立意与追求——傅种孙先生《扩张与因袭》阅读体会

☉江苏苏州市相城区渭塘第二中学 陈惠英

扩张与因袭：问题情境的立意与追求
——傅种孙先生《扩张与因袭》阅读体会

☉江苏苏州市相城区渭塘第二中学 陈惠英

近读《中学数学（下）》，其中刊发了几篇傅种孙先生著作的阅读体会与教学实践，据笔者有限的阅读经历，傅种孙先生的研究和纪念文章多是北师大不少教授、研究者们写的，当下的一线教师能主动关注我国老一辈像傅种孙先生这样的数学教育家的著作文献的还不多见.本文是阅读傅孙先生名作《扩张与因袭》的心得体会，与大家分享.

一、《扩张与因袭》精彩摘录与随感

第一，何谓扩张？

傅先生在该文开篇即指出：“中学数学教师们领着学生走一条康庄大道：‘由整数走向分数，由正数走向负数，由有理数走向无理数，由实数走向虚数’.这是在那里扩张数系.”在引述一些例子之后，傅先生强调“数系扩张之原因，本有事实需要的背景在，故亦需有实例引之”.

随感：初中数学在各个知识领域都有着“扩张”，比如，整式到分式再到无理式，一元一次方程到二元一次方程再到一元二次方程等；学习函数时从最简单的正比例函数出发，到一次函数、反比例函数、二次函数等；就平面几何的学习来看，从点到线到面到体，从三角形内角和到四边形内角和再到多边形内角和，平行四边形的学习从边、角、对角线依次研究它的性质与判定，并扩大到与平行四边相关的一些性质（如三角形中位线定理、直角三角形斜边上中线的性质）等.

第二，何谓因袭？

傅先生指出“扩张数系后，同时又希望‘整数的性质分数也有，正数的性质负数也有，有理数的性质无理数也有，实数的性质虚数也有.’这是在那里因袭数性.”在列举很多具体的例子之后，傅先生在该文有一段深刻小结：因袭不是无限制的，一成不变是不行的.究竟变的是什么，不变的是什么？数系之因袭，特为和、美、不别扭计耳；可因袭者因袭，应变革者变革；法规既立，而后应用之于事例，可用者用，不可用者不用.其因也，革也，用也，不用也，原因皆在实际事例之本身，非可以论理方法形式地判断者也.

随感：以数的运算为例，有理数引入之后，首先是相关概念（数轴、相反数、绝对值等），在此基础上为研究、归纳有理数运算法则提供了一些必要的概念准备，比如正负数加减法则不同于小学算术数的加减运算；而两个负数相乘也是新的内容，找不到因袭的法则，则属于傅先生指出的“应更革者更革”.而在有理数的运算，特别是混合运算时，又需要因袭之前学生在小学算术学习过程中积累下来的运算通性（加法交换律和结合律、乘法对加法的分配律等），包括运算顺序（同级运算从左向右依次运算，通过添加括号可以改变运算顺序，使得不同运算享有“插队”的优先级别）.

在学习方程时，比如最先系统学习的一元一次方程，往往先学习一元一次方程的概念、一般形式，然后学习如何解一元一次方程，最后研究如何利用一元一次方程解决实际问题.因袭这样的研究套路，二元一次方程、一元一次不等式、一元二次方程都有类似的研究套路：概念、解法、应用.

在几何图形的学习时，一个大的研究范式是平面几何主要研究图形的形状、大小与位置.具体到一些特殊图形，如三角形，先研究它的概念（定义、边、角）、相关概念（高线、中线、角平行线）、内角和定理、外角和定理，接着研究特殊三角形（如直角三角形）的角、边的性质，这些研究经验将因袭到四边形的研究，如先研究四边形的定义，边、角、对角线的性质，并研究特殊四边形（如平行四边形及矩形、菱形、正方形）的性质.

需要指出的是，以笔者粗浅的理解，近年来人民教育出版社资深编审章建跃博士在相关文章中推荐的“研究套路”，也与傅先生所指出的因袭在一定意义上是相通的说法.

二、对新知引入阶段“问题情境”的相关思考

众所周知，数学是一个逻辑连续的整体，同一数学领域、知识块的逻辑联系十分紧密，就是不同领域也有非常密切的关联.傅先生关于扩张与因袭的论述引发我们对新知引入阶段“问题情境”的再思考.

1.教材盛行“生活情境”，追求有“数学味”的数学现实.

新世纪之初的课程标准片面倡导数学生活化，与生活情境关联，随之而来的教材改革也“执行”了这种编制要求，使得世纪之初的各种版本教材几乎每个课时都由一段丰富多样的生活情境导向新课、新知，完全置数学知识的“扩张”于不顾，误以为每个数学知识都必须来源于生活现实.尽管“课标2011年版”已对生活情境做出必要的纠偏，认为生活现实与数学现实要根据数学知识的内在逻辑联系灵活选取，同时要注意兼顾其他学科现实，然而教师形成的教学惯习并不是一朝一夕所能改过来的，加之推行生活情境引入新课的各种“三维目标”的教案推波助澜，让很多教师误认为课堂引入时用一段有趣的生活情境，可以为课堂增色、形成亮点，又使得数学有趣.我们认为，重温傅先生的扩张与因袭有助于我们追求更有数学味的数学现实来导入新课，而不是简单化地舍弃教材上的情境问题.有些对教材上的情境问题基于扩张与因袭的思想，将其重组，也可以获得更有意义的教学情境.

比如，某版本初中教材九年级一元二次方程起始课的教学引入是一段矩形花圃问题情境，如果我们适当加以改编，也可成为体现扩张与因袭的教学情境.

案例1：如图1，矩形花圃的一面靠墙，另外三面所围的栅栏的总长度是19m.

图1

（1）如果花圃的长比垂直于墙面的宽多4m，设它的宽为xm，它的长为________m.

（2）如果花圃的面积是24m2，设花圃的宽是xm，它的长为________m.

设计意图：利用教材上的这段情境，先设计一个铺垫问题，既复习了一元一次方程的应用，又为下一问列出一元二次方程提供了知识准备，我们可以引导学生比较这两个方程的相同点与不同点.并在比较中，由学生自主归纳出一元二次方程的概念.这也体现了扩张与因袭的教学思想.

2.“开课情境”孤立化，让“问题情境”驱动全课学习.

在不少赛课活动中，往往都会安排所谓的情境引入，然而这种开课阶段的问题情境往往孤立于全课，即在完成了所谓的概念引入甚至是某个并不重要的标题、名词的引入之后，这个情境就完成了历史使命，与后续教学环节无甚相关.如在平方根（第1课时）开课引入时，有教师设计如下的情境引入：

案例2：探究怎样用两个面积为1的小正方形拼成一个面积为2的大正方形.

你能用两个面积为1的小正方形拼成一个面积为2的大正方形吗？裁剪下这两块面积为1的正方形纸，看能否直接拼接.（合理分工，发挥集体智慧，进行剪、拼、接，拼好后，画出你的方案并展示）

案例3：（定义开方运算后，结合“x2=4”研究平方根的定义、求法、符号表示、性质），教学流程如下：

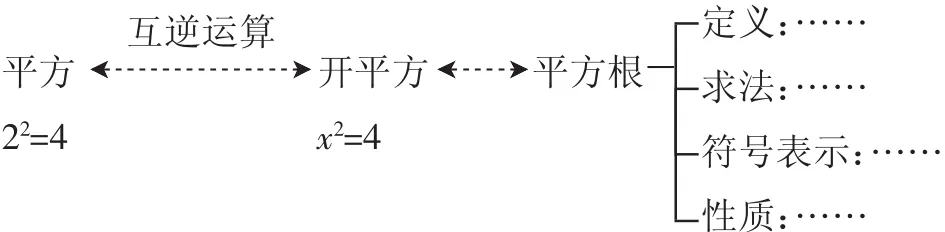
赏析：在上面的教学流程中，对于平方根的求法、符号表示的学习，学生小组内举例、交流、讨论，性质发现、归纳也由学生完成.

3.精选“数学现实”，让学生明辨、体会“扩张与因袭”.

具体落实在备课时，我们认为精选数学现实是备课的关键，比如二次根式乘法运算的引入时，目前相关教材已修改为如下的开课情境：

案例4：计算下列各式，观察计算结果，你能发现什么？

一般地，二次根式的乘法法则是________________ ____________________.

简评：通过这组运算，学生可以自主发现、归纳出二次根式的运算法则，感受到二次根式运算与之前的整式运算之间的“同与不同”，体现其中的扩张与因袭的数学思想.

三、写在后面

傅种孙先生数学教育思想博大精深，本文只是受益于傅先生《扩张与因袭》一文，思考了情境创设中的一些话题，收集和展示的案例还不够丰富，有待进一步研究与积累，也期待更多的同行深入研习傅先生的扩张与因袭的数学思想，研发出精彩的课例，让这个课题深入下去、丰富起来.

1.傅种孙.扩张与因袭［J］.数学通报，1962（8）.

2.傅种孙.傅种孙数学教育文献［M］.北京：人民教育出版社，2005.

3.陈蓓蓓.例说几何定理教学的层次——由傅种孙先生数学教育思想说起［J］.中学数学（下），2016（12）.

4.王锦兵.朝花夕拾读经典，基本问题能致远——研读《中学数学》2016年12月初中版有感［J］.中学数学（下），2017（1）.

5.刘东升.悠然神会，妙处与君说——李庾南老师“平方根”课例赏析［J］.中国数学教育，2014（5）.

6.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

*本文是江苏省“十二·五”规划青年自筹课题“优化与导学案匹配的初中数学课堂教学结构”的研究成果（课题编号：C-b/ 2013/02/004，主持人：孙学东）；也是江苏省“十三·五”规划重点自筹课题“初中数学深度学习资源建设的实践与理论研究”的阶段成果（编号：B-b/2016/02/155，主持人：周建勋，孙学东）.