形散神聚“关联题”，洞察结构练眼力——再谈中考二轮复习

☉江苏苏州市吴江区松陵第一中学 沈丽婧

形散神聚“关联题”，洞察结构练眼力
——再谈中考二轮复习

☉江苏苏州市吴江区松陵第一中学 沈丽婧

拙文《聚焦微专题：中考二轮复习的实践与思考》（详见文1）记叙了笔者在中考复习期间对一组关联试题的归类整理与共性挖掘，发表在《中学数学（下）》之后，不少同行纷纷点赞、给予鼓励，这又促进我深入思考这一话题，即中考二轮复习应该怎样组织教学内容，如何引导学生把同类习题梳理归纳、发现结构，有效提升解题能力和解题速度.本文还将从文1中的一道例题出发，同类链接，跟进思考关联试题，供研讨.

一、考题与同类链接

题1：（2013年江苏南通中考题，第28题）如图1，直线y=kx+b（b＞0）与抛物线相交于A（x，y）、B（x，y）

1122两点，与x轴的正半轴相交于点D，与y轴相交于点C.设△OCD的面积为S，且kS+32=0.

（1）求b的值；

（2）求证点（y1，y2）在反比例函数的图像上；

（3）求证x1·OB+y2·OA=0.

图1

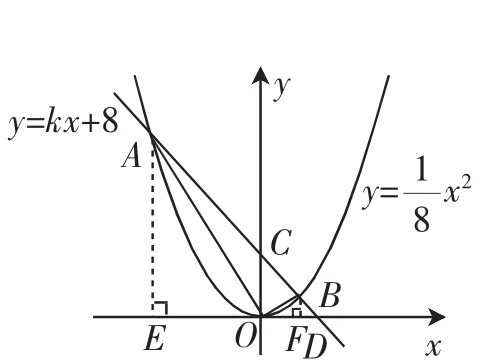
图2

思路简述：限于篇幅，（1）和（2）的解答略去；（3）如图2，构造并证出△AEO∽△OFB.可得，即.从而变形得x·OB+y·OA=0.12

结构反思：如图1，直线y=kx+b（b＞0）与抛物线y=ax2相交于A（x1，y1）、B（x2，y2）两点，与x轴的正半轴相交于点D，与y轴相交于点C.当a·b=1时，△AOB一定是直角三角形.

考题2：（同类链接题）如图3，在平面直角坐标系中，抛物线与x轴交于点A（-1，0）、B（-3，0），与y轴交于点C，顶点为D，抛物线的对称轴与x轴的交点为E.

（1）求抛物线的解析式及E点的坐标；

（2）设点P是抛物线对称轴上一点，且∠BPD=∠BCA，求点P的坐标；

（3）若过点E的直线与抛物线交于点M、N，连接DM、DN，判断DM与DN的位置关系并说明理由.

图3

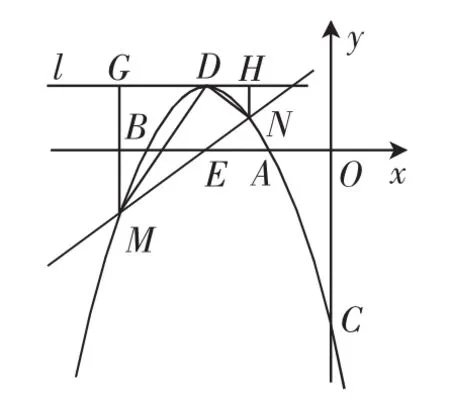
图4

思路简述：限于篇幅，直接给出前两问的答案，y= -x2-4x-3，E（-2，0）、P1（-2，-2）、P2（-2，2）.

（3）如图4，受到“一线三直角”基本图形的启示，我们过点D作x轴的平行线l，分别过点M、N作MG⊥l，NH⊥l.设过点E（-2，0）的直线的解析式为y=kx+b，则-2k+b= 0，即b=2k，所以y=kx+2k.设M（m，-m2-4m-3）、N（n，-n2-4n-3），则MG=1+m2+4m+3=（m+2）2，GD=-2-m，DH=n+2， HN=1+n2+4n+3=（n+2）2.再写出它们的比例式MG= GD.接下来的难点就是：这两个比例式能否相等？关键就是证明下面就突破这个难点：

于是难点得到突破.结合∠G=∠H=90°，可证△MGD∽△DHN，从而证得DM⊥DN.

解后反思，结构认识：现在让我们把问题重新梳理，我们知道平移图形并不会改变对应线段前后的数量关系、位置关系，所以我们可以考虑将抛物线适当平移，使得点D恰为坐标原点，点E为（0，-1），这样就可以认识到此时抛物线的解析式为y=-x2，直线方程为y=kx-1.这是满足我们在考题1的结构反思中提出的规律的：当a·b= -1×（-1）=1时，△DMN一定是直角三角形.

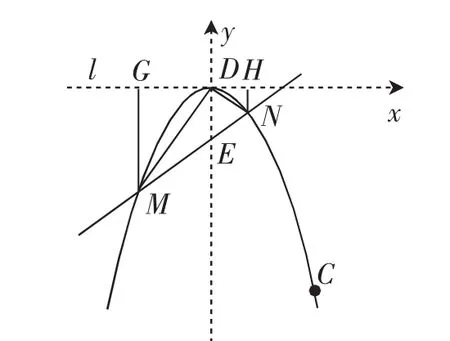
图5

教学手记：在给学生讲评考题2的第（3）问原解法时，不少学生对思路都能理解，但表示运算量太大，不能顺利算出结果.后来补充了图5这样的变换坐标系的解法之后，大家都表示能理解这种解法，因为这样做“回”到了考题1的思路，使得繁杂的运算变得较为简洁.

二、关联试题的收集与整理

罗增儒教授在《解题学引论》一书中曾提出模式识别策略，认为首先要积累模式，然后注意收集模型的可能变式，并在再次碰到相关模式时，能精准识别、迅速确认模式，并提取与该模式相关的解题经验实现问题的解决.我们在本文提及的所谓关联试题，也是倡导教师在备课、上课、课后研习试题时要注意对关联试题进行收集和归类整理，以便于通过长期的教学实践，积累大量的关联试题，从而在解题教学时能灵活选用甚至信手拈来.以下是一些相关的建议.

1.从教材例、习题出发，收集典型中考变式问题.

教材是精心打磨的教学蓝本，认真研习教材例、习题对于提高教师专业素养有很大的帮助.如章建跃博士所指出的当前有些学校编制所谓的习题单式的导学案，而让教材旁落，甚至有些学校平时上课基本不使用教材，这种现象必须得到纠偏.一个值得开展的工作就是教师在认真研究教材例、习题的基础上，结合手头收集到的中考题或地区经典考题，进行归类存档，把与教材例、习题高度相关的考题整理到一起，形成同类题库，这样有利于备课时随时提取.

2.聚焦初中主干知识，跨不同年级收集关联题.

在收集整理关联试题时，要注意关注初中数学主干知识，以主干知识数轴为例，从初一到初二再到初三，可以将关联题整理到一起，在初一数轴学习仅限于数与形的对应，数轴上两点间距离公式；到初二时与平面直角坐标系关联起来，两个点可以拓展到直线x=a、y=b上进行研究，对一些优秀学生还可以提前让他们探究任意两点间距离公式.再比如，初一学习两角互余时，可拓展到直角三角形中两个锐角互余，到平行线性质与判定学习时，会遇到“两直线平行，则它们的同旁内角的平分线互相垂直”这样的命题证明，本质上也会与两角互余有关联；而初二全等三角形学习之后，两个全等的直角三角形之间常常有互余关系的探究；到初三相似三角形中一个经典模型“射影定理”（或双垂直三角形），进行关联收集，便于教学时引导学生对比体会.

三、关联试题的教学建议

1.中考二轮复习要重视针对关联试题的专题辅导.

从目前中考二轮复习的很多复习资料或学校公开课、研讨课来看，二轮复习关注的主题仍然是所谓的题型聚焦，即开放专题辅导、运动专题辅导、阅读理解专题辅导、新定义专题辅导等，这样的专题设置固然也有一定的合理性，然而根据我们的教学实践，如果能在这些专题框架下，选题时加大关联试题作为例题或题组的设计，则教学效益会大大提升.通过这些关联试题集中呈现，促进学生从形散的试题走向神聚理解，并学会洞察问题结构，训练眼力，以便在惜时如金的考场上，迅速识别这些试题的结构，为贯通思路获得宝贵的时间.

2.引导学生整理关联试题，随时丰富充实相关专题.

郑毓信教授倡导的开放式教学近年来得到有关老师的实践，我们在《中学数学（下）》也零散见到一些案例研究的文献.受到启示，在引导学生整理关联试题，或开展相关主题的关联例、习题讲评时，在课堂小结阶段，应该告知学生这个专题还没有结束，关联试题的讲评只是开启这一主题的一扇窗，在以后的解题学习时，再遇到同类结构习题时，要随时丰富充实到这个专题下，这事实上就是一种特色专题收集，也是错题集的有效完善.

四、写在后面

中考复习年年进行，岁岁年年花相似.如何上出新意，让老歌新唱，让学生在复习期间也能培养创造性思维呢？笔者认为，如果我们能提供足够的关联试题，学生就会时时感受到数学是联系的，是一个整体，而不是孤立的，这样对数学整体观、系统观、广泛联系也就能深刻理解.这是笔者针对中考二轮复习案例思考的第二篇习作，仍然是初步的，希望得到批评和指导，也期待更多关联题例，丰富这个研究课题.

1.沈丽婧.聚焦微专题：中考二轮复习的实践与思考——以一组“关联试题”复习为例［J］.中学数学（下），2017（3）.

2.刘才云.源于教材高于教材，辨识特征眺望远方——对一份七上期末卷的赏析与思考［J］.中学数学（下），2017（2）.

3.秦怡.回到概念，让解题念头“自然生成”——从一道几何难题的思路突破说起［J］.中学数学（下），2017（2）.

4.王成.同类链接促进感悟，模考讲评提升效益——以一次模考题的链接讲评为例［J］.中学数学（下），2017（2）.

5.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.