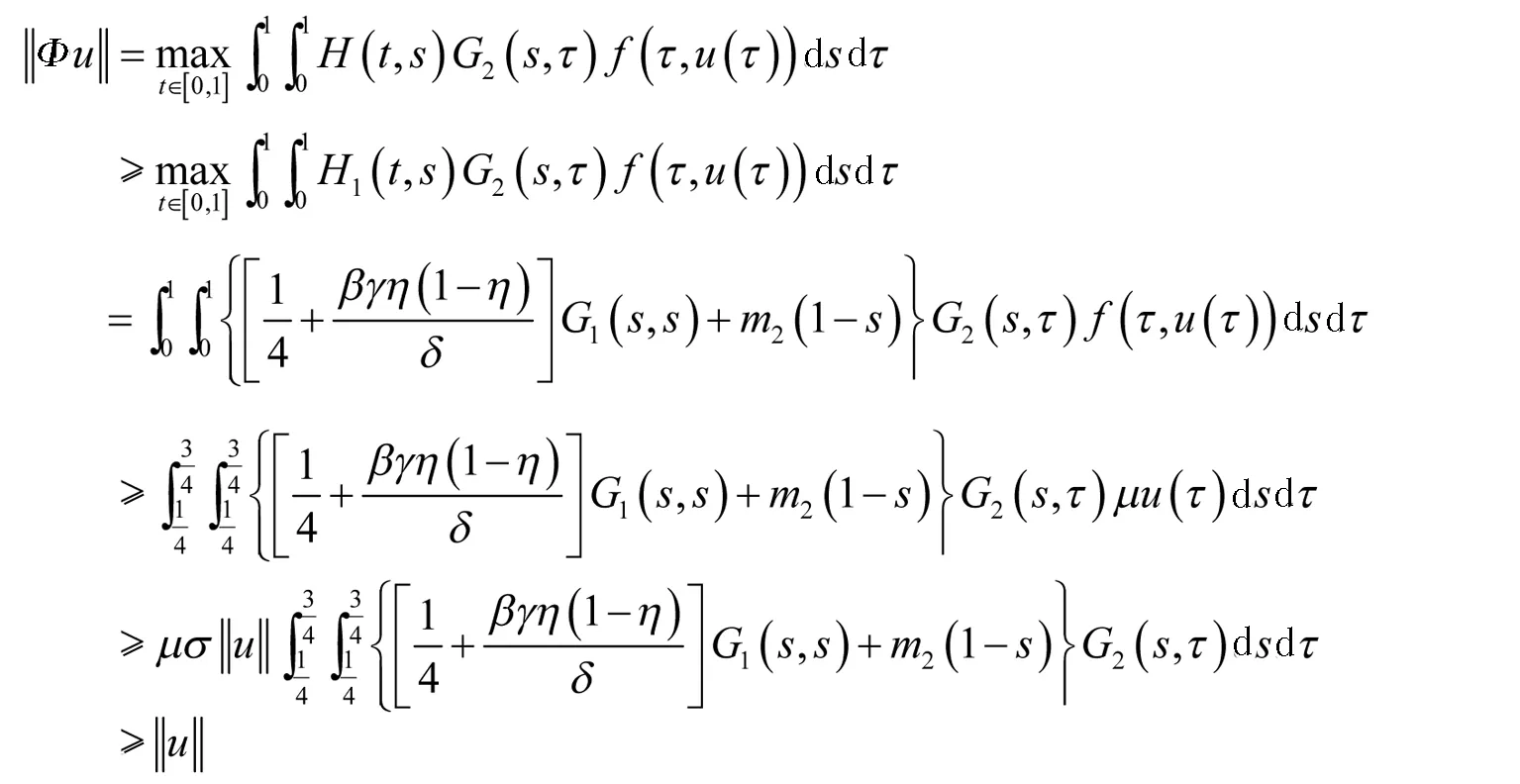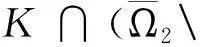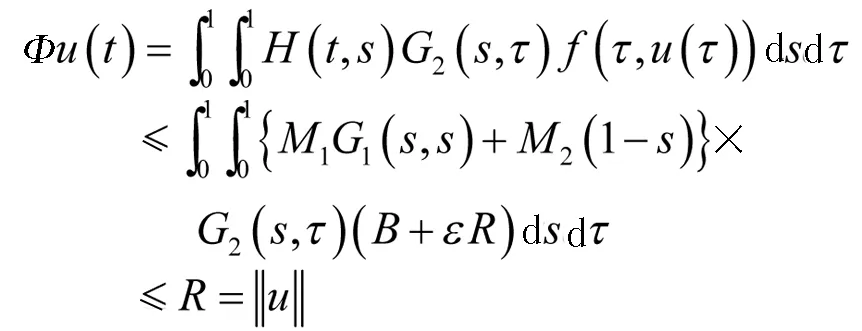非线性四阶多点边值问题的正解*

赵冬霞,张 玲,田淑杰

( 1.大庆师范学院; 2.东北石油大学)

0 引言

非线性四阶边值问题在物理学中的流体力学、弹性力学等领域问题中有着广泛的应用和研究，尤其是其正解具有深刻的意义，不少作者都曾对此问题有过研究，并且得到了一些结论.该文讨论包含参数的非线性四阶多点边值问题，当参数属于一定范围时，得出问题的正解.

1 问题与假设

研究非线性四阶边值问题，即

其中α,β均为正数，满足0<γ<1，而ρ>0是参数．对上面的边值问题进行讨论，讨论在什么条件下存在正解，并对正解的存在性进行证明.先构造出Green函数，然后将上面的边值问题的微分形式转化为单个积分的积分方程,并利用锥拉伸与压缩不动点定理[1]证明其正解的存在性.

假设：

定义1 称函数u(t)为边值问题式(1)的正解，如果它满足u∈C1[0,1]∩C2(0,1)，在(0,1)内u(t)>0，并且u(t)满足边值问题(1)[2].

定理1 假设(H1),(H2)或(H1),(H3)成立，则边值问题式(1)至少存在一个正解．

引理1 设a,b,c是实常数，φ1(t),φ2(t)是方程av″(t)+bv′(t)+cv(t)=0的2个无关解，φ0(t)是边值问题

的一个解，则φ(t)=c1φ1(t)+c2φ2(t)+φ0(t)是方程av″(t)+bv′(t)+cv(t)=h(t)的通解，其中c1,c2是任意常数．

证明直接验证即可．

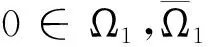
(1)‖Φu‖≤‖u‖，u∈K∩∂Ω1；并且‖Φu‖≥‖u‖,u∈K∩∂Ω2或

(2)‖Φu‖≥‖u‖,u∈K∩∂Ω1;并且‖Φu‖≤‖u‖,u∈K∩∂Ω2,

引理3 ∀s,t∈[0,1]成立不等式

t(1-t)G1(s,s)≤G1(t,s)≤G1(s,s),

(*)

(**)

G2(s,s),

(***)

(****)

证明∀s,t∈[0,1]有

即可证得式(*)．特别，由式(*)知η(1-η)≤G2(η,s)≤G1(s,s)，便可证得式(**)，利用Taylor公式，并注意到eρs-e-ρs的单调性，可知

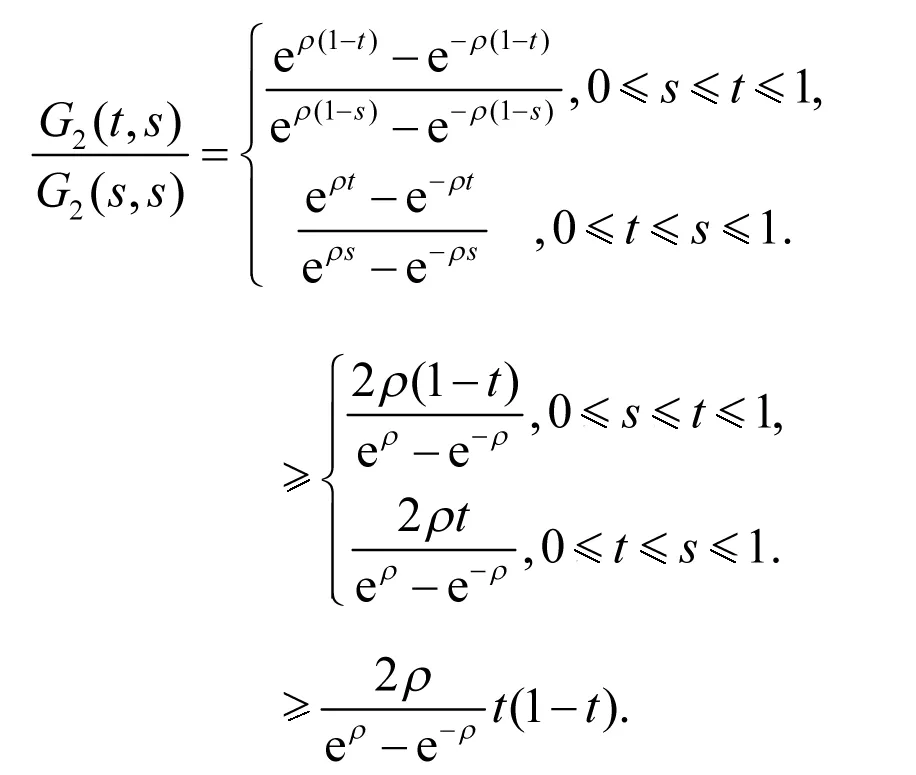
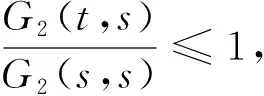
2 边值问题的等价形式及格林函数

令u″(t)=-v(t)，则有

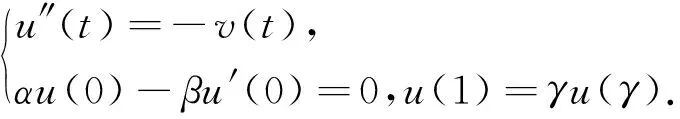
(2)

首先对非线性三点边值问题进行研究

容易知道边值问题

又由于φ1(t)=t,φ2(t)=1-t是u″(t)=0的2个无关解，根据引理1知边值问题式(2)等价于积分方程

并满足条件u(0)=0,u(1)=0，也即有

由边值问题(2)的边界条件

整理可得

另记δ=α(1-γη)+β(1-γ)，则由克拉默法则可得确定c1,c2为

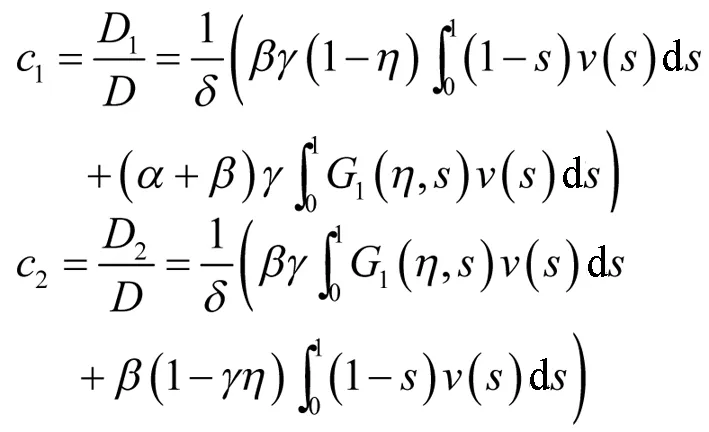
可知边值问题式(2)等价于积分方程

整理得

然后再对非线性两点边值问题进行研究

(4)

上述的非线性边值问题(4)可以很容易的转化为如下的等价积分方程

其中令

并将v(t)表达式带入u(t)表达式中得到

(5)

引理4 ∀s,t∈[0,1],成立不等式

证明∀s,t∈[0,1]由引理3得

t(1-t)G1(s,s)≤G1(t,s)≤G1(s,s)

η(1-η)G1(s,s)≤G1(η,s)≤G1(s,s)

因此

H(t,s)≥t(1-t)G1(s,s)+

又

3 正解的存在性

设C[0,1]是[0,1]上全体连续函数构成的Banach空间，C[0,1]={u∈C[0,1];u≥0}，定义映射Φ:C[0,1]→C[0,1]

记

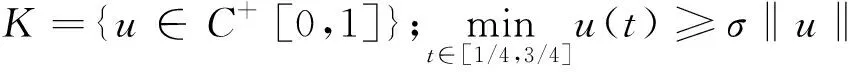
引理5Φ:K→K全连续．

证明∀u∈K,由引理3知

再令

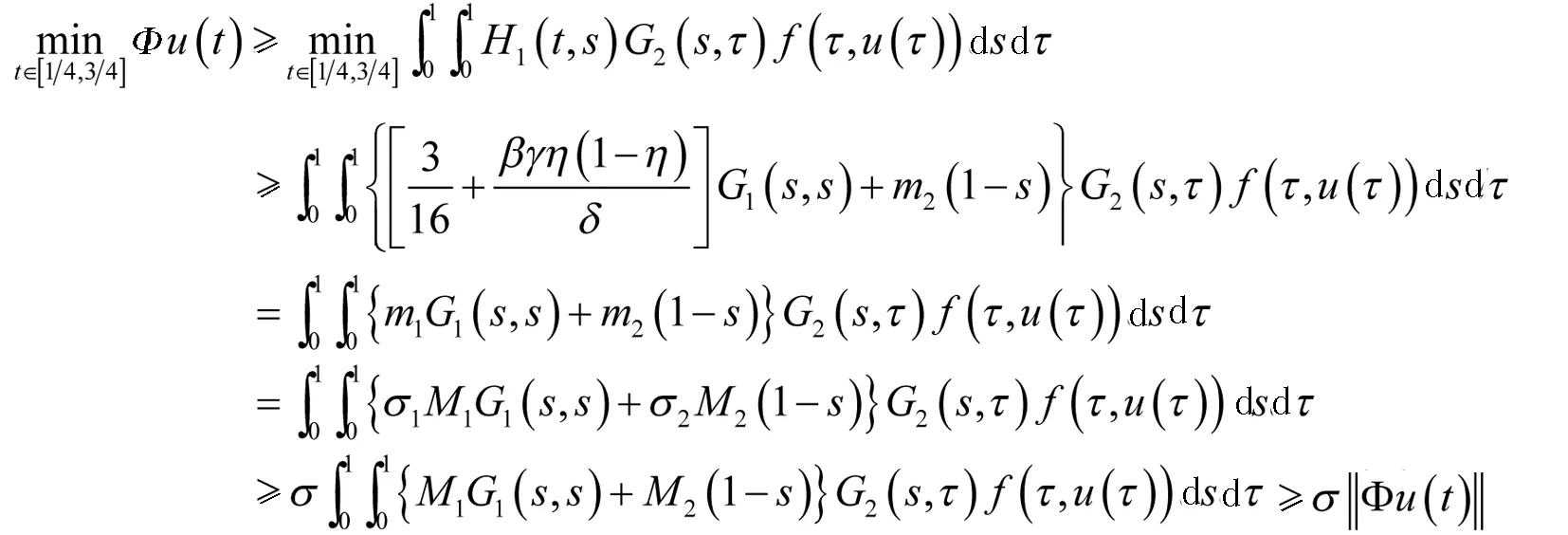
因此Φu∈K，即Φ(K)⊂K，另外容易证明Φ是全连续的.

4 正解存在性证明

假设(H1),(H2)成立．由(H2)知存在r>0，使当0≤u≤r时有f(t,u)≤εu，这里ε>0,满足

G2(s,τ)f(τ,u(τ))dsdτ≤1.

取Ω1={u∈C[0,1];‖u‖

即有‖Φu‖≤‖u‖．

再由(H2)知存在R1>0，使当u≥R1时有f(t,u)≥μu，此处μ>0满足

因此，由引理4知

即有‖Φu‖≥‖u‖．

假设(H1),(H3)成立．由(H3)知存在r>0，使当0≤u≤r时，有f(t,u)≥μu,这里μ>0

满足

设Ω1={u∈C[0,1];‖u‖

即‖Φu‖≥‖u‖．

再由(H3)知存在H>0，使当u≥H时有f(t,u)≤εu，这里ε>0使

则有

令Ω2={u∈C[0,1];‖u‖

即有‖Φu‖≤‖u‖．

若f (t,u)有界，则存在N>0，使对t∈[0,1]和u∈[0,+∞)有f (t,u)≤N，取

令Ω2={u∈C[0,1];‖u‖

即‖Φu‖≥‖u‖．

参 考 文 献

[1] Guo Dajun, Lakshmikantham V. Nonlinear problems in Abstract Cone[M]. Boston: Aeademie Press, 1988.

[2] 禹海兰, 裴明鹤. 两类四阶非线性常微分方程两点边值问题解的存在性[J]. 东北电力学院学报,2002(4):53-57.

[3] 赵冬霞.二阶非线性三点边值问题的正解[J].大庆师范学院学报,2013(11):28-32.

[4] Bai Chuanzhi, Yang Dandan, Zhu Hongbo. Existence of solutions for fourth order differential equation with four-point boundary conditions[J]. Applied Mathematics Letters, 2007(20):1131-1136.

[5] 郭晓霞, 张克梅. 非线性四阶常微分方程两点边值问题解的存在性[J].曲阜师范大学学报:自然科学版,2008(4):19-26.

[6] Yang Yang, Zhang Jihui. Nontrivial solutions for some fourth order boundary value problems [J]. Nonlinear Analysis，2009 (70):3966-3977.

[7] 孙忠民, 赵增勤, 任锁全.单边Nagumo条件下四阶微分方程边值问题正解的存在性[J].高校应用数学学报,2008(1):61-66.