结构方程模型在评价高校通识课中的应用

王赵志，谢国忠，梁绍佳，邓双娇

（1.肇庆学院，广东 肇庆 526061；2.鼎湖区实验中学，广东 肇庆 526070；3.鼎湖区广利初级中学，广东 肇庆 526073）

结构方程模型在评价高校通识课中的应用

王赵志1，谢国忠2，梁绍佳3，邓双娇1

（1.肇庆学院，广东 肇庆 526061；2.鼎湖区实验中学，广东 肇庆 526070；3.鼎湖区广利初级中学，广东 肇庆 526073）

为研究探索真实可靠的通识课程评价方法，从学生对通识课满意度入手，建立学生对通识课评价的研究假设模型.将通识课评价因素分为预期教学效果、感知课程质量、感知课堂效果、感知学习收获、满意度和忠诚度6个潜在变量，17个可观测变量，进行问卷调查并进行信度分析，运用结构方程模型对假设模型进行分析验证.总体上模型的拟合度较好，6个研究假设都得到支持.在结果分析的基础上提出提高高校通识课教学效果的建议.

通识课；结构方程；模型；课程评价

通识教育对大学生进行基础科学知识传授、公民意识培养、健全人格熏陶和某些非专业性的实操能力培养[1]，对大学生全面发展具有重要作用.随着通识教育在高校逐步普及，通识课的评价问题日益受到关注.现在主要是从高校行政管理和教师的角度进行研究，很少从学生的角度分析.目前我国通识课评价研究方法主要有：得菲尔法、因子分析法、主成分法、模糊-综合判别法、成分分析法等，这些方法主观色彩浓厚，指标要素依靠主观臆断确定，影响评价结果的可靠性和真实性.

结构方程模型(structural equation modeling简称SEM)符合定量研究分析在深层次方面的要求，能够揭示教育研究过程中内在复杂机制，具有克服回归、相关、路径分析等统计方法弊端的特点，受到国内教育研究者的关注.为研究通识课评价方法，从学生对通识课的满意度入手，对肇庆学院通识课进行评价研究，构建结构方程模型进行分析验证，并从学校行政管理、教师及学生等各方面提出通识课教学改进的建议.

1 研究模型与假设

20世纪90年代以来，很多国家开展了顾客满意度指数测评工作[2].目前，顾客满意度主流模型为瑞典顾客满意度晴雨表模型（SCTB）、美国顾客满意度指数模型（ACSI）和欧洲顾客满意度指数模型（ECSI）[3]等，其中ACSI模型得到了最广泛的应用.为开展通识课评价研究，以学生对课程的满意度为切入点，根据通识课组织与教学的特点，对美国顾客满意度指数模型(ACSI)进行调整[4]，提出学生对通识课的满意度模型，包括6个潜在变量[5]：

1）预期教学效果：学生在接受通识课教育之前对其质量做出的估计和期望，包括实用性预期，对老师的预期，学习兴趣和总预期.

2）感知课程质量：学生在接受通识课教育过程中对其质量做出的感知评价，包括知识的实用性和新颖性，案例数量，例题与练习.

3）感知课堂效果：学生感知通识课的课堂氛围以及对老师的综合评价，包括课堂氛围，教师的能力以及可靠性感知.

4）感知学习收获：学生对通识课程所学知识和收获的综合评价，包括知识掌握情况，考试信心.

5）满意度：学生对通识课的综合满意程度，包括总体满意度，与预期的差距，与理想的差距.

6）忠诚度：学生对通识课的忠诚程度是学生对满意度的行为表现，包括全勤率，推荐概率.

在分析的基础上作出相关假设模型，假设6个潜变量间关系如图1所示，图中H1到H6为假设的相邻2个潜变量之间的影响关系，箭头所指方向为正向影响关系：H1为预期教学效果对感知课程质量有正向影响；H2为感知课程质量对感知课堂效果有正向影响；H3为感知课堂效果对满意度有正向影响；H4为预期教学效果对感知学习收获有正向影响；H5为感知学习收获对满意度有正向影响；H6为满意度对忠诚度有正向影响.

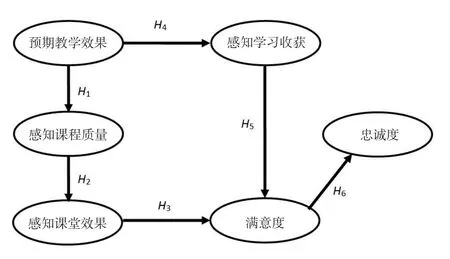
图1 通识课学生满意度研究模型

2 研究过程与数据分析

2.1 问卷设计和数据采集

经研究借鉴有关通识课教学调查问卷，结合肇庆学院通识课程情况，设计了调查问卷，共17个问题，涵盖了预期教学效果、感知课程质量、感知课堂效果、感知学习收获、满意度和忠诚度等6方面内容.为准确掌握学生感受，问卷中的问题采用李克特(Likert)10级量表[6]（1代表“非常低”或“非常差”，10代表“非常高”或“非常好”）进行测量，要求接受调查学生根据真实感受回答.调查对象为肇庆学院2011级学生52人、2012级43人、2013级33人，总有效样本128个.模型的潜变量、可观测变量(a)和对应问题如表1所示.

表1 潜变量、可测变量及对应问卷问题

2.2 问卷信度分析

用SPSS17.0软件对模型数据进行内部一致性的信度分析，并校对异常数据.内部一致性信度通常用Cronbach’s Alpha值衡量[7]，系数值在0.9~0.8为极好；0.8~0.7为较好；0.7~0.65为最小可接受值.模型拟合得到的6个潜变量的Alpha值分别如表2所示，总的可靠性统计量的Cronbach’s Alpha系数如表3所示.由表2可知Alpha系数均大于0.7，由表3可知总的可靠性统计量的Cronbach’s Alpha系数已达0.928，表明此数据具有较高的内在一致性，问卷的设计也具有较高的信度.

2.3 结构方程模型分析

结构方程模型可替代回归分析、方差分析、对应分析、因子分析、聚类分析等方法，清晰分析单项指标对总体的作用及单项指标间的相互作用关系.根据问卷统计情况，并通过大量的试算和调整，得出如图1所示较合理的结构方程模型.在该结构方程模型分析中，均采用AMOS 7.0软件对模型的数据进行拟合，其输出的路径标准化系数及模型见图2所示，椭圆中的变量为潜变量，方框中的a变量为可观测变量，圆圈内e表示残差，箭头旁所标注的数字是影响系数.

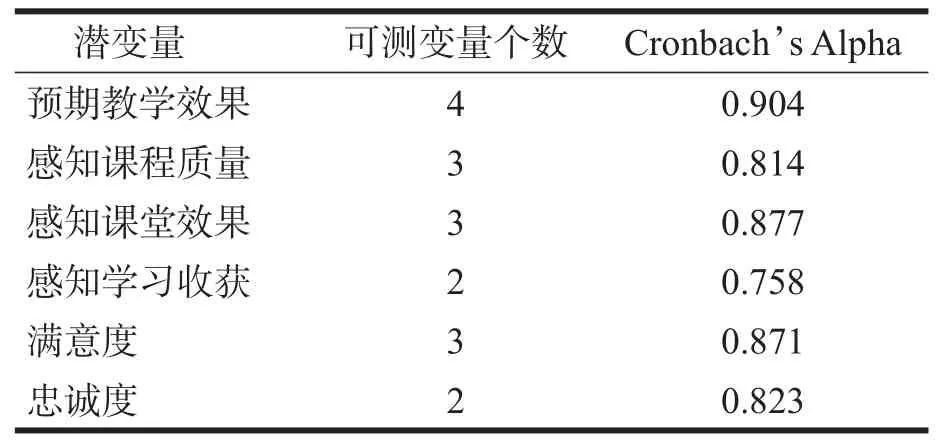
表2 潜变量的信度检验

表3 信度分析结果

图2 通识课学生满意度结构模型路径系数图

为精准地验证该模型的拟合度，选取常用的拟合指标（如表4所示）如卡方自由度比值（CMIN/DF）、拟合优度指标（GFI）、规范拟合指数（NFI）、相对拟合指数（TLI）、近似均方根残差（RMSEA）以及信息标准指数（AIC）和研究假设（如表5所示），对其进行验证，验证结果表明，该模型的指标均达到可以接受的水平，模型总体上的拟合度较好.

表4 模型拟合指标对比

根据图1提出的6个研究假设进行验证，验证结果如表5所示，6个研究假设都得到支持.

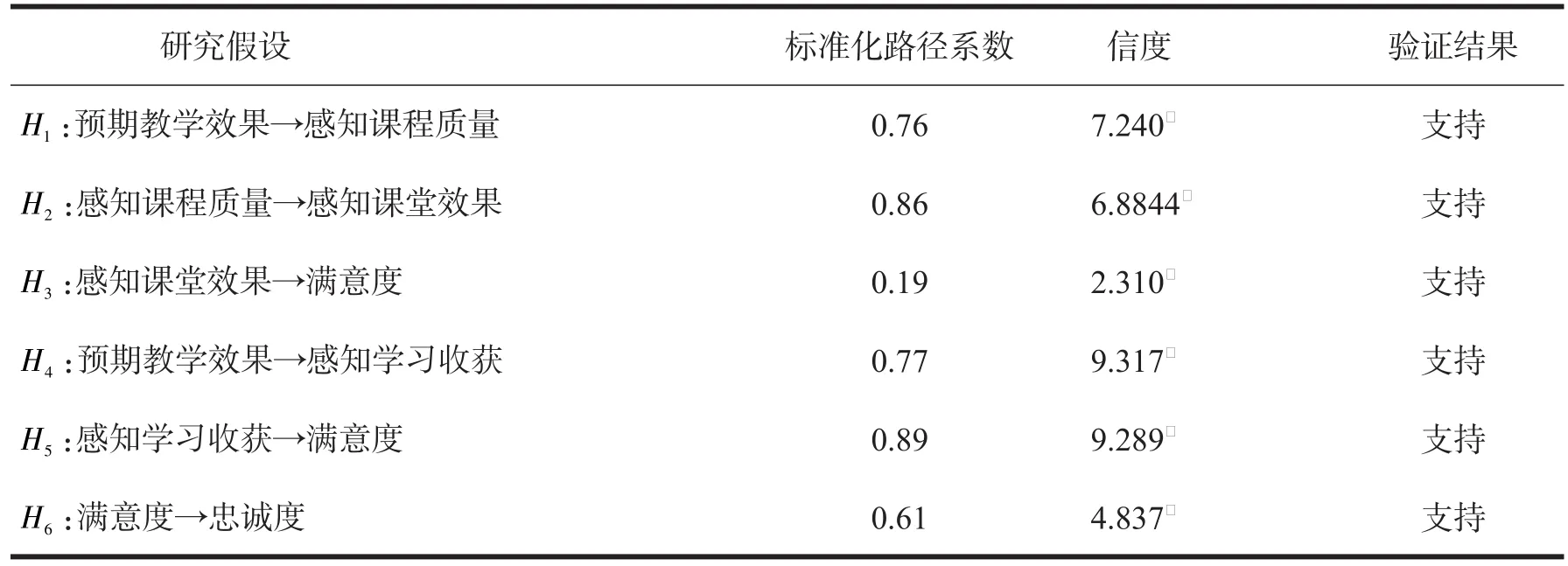
表5 研究假设验证结果

2.4 结果分析

根据模型分析得到如下结果：

1）由于感知课程质量和满意度之间的直接路径系数没有通过显著性检验[9]，说明感知课程质量与满意度之间并无直接的路径关系，但感知课程质量是直接对感知课堂效果产生影响继而对满意度产生间接的影响.在最初模型的试算和调整时已经发现，如果在感知课程质量与满意度之间建立直接路径关系，最后会导致模型无法识别.因此，感知课程质量是通过对感知课堂效果产生直接影响，从而对满意度产生间接影响.

2）满意度与忠诚度有显著的路径关系.提高学生对课程的满意度，能够使该课程更受学生的欢迎，并同时提高学生学习该课程的积极性与主动性.

3）由表5研究假设验证结果可知，感知学习收获对于满意度的影响最大.因此，今后的教学改进措施应着重提高学生自身感知的学习收获，这就要求教师必须合理设计通识课的教学内容，帮助学生搭建已有知识和新知识之间的认知桥梁.除此之外，建议通过合理的考察方式增加学生的学习成就感，多开展实践性教学，将课程的理论知识和实践相结合.

3 结论与建议

本研究以肇庆学院学生为研究对象，利用结构方程模型分析高校学生对通识课的满意度，得出重要结论：（1）学生自身感知学习收获直接影响通识课的满意度；（2）提高学生对通识课的满意度，可以激发学生学习该课程的积极性，增强对该课程的忠诚度；（3）预期教学效果间接影响通识课的满意度.基于上述分析，提出以下优化通识课程教学的建议.

1）学校管理方面：建立奖励淘汰制度，切实提高教师的业务水平；定期定量地开展相应的教学调查研究，充分挖掘学生对通识课的实际需求与潜在需求，构建起科学合理的课程体系；建立反馈机制，及时了解通识课的实际质量和学生期望质量之间的差距，并进行合理的调整和改进，为学生提供满意的教学质量；多开展实践性教学活动激发学生的学习兴趣；提高对通识教育的重视，建立通识课程教学指导中心，加强通识课程的师资队伍建设和逐步完善教学评价制度[10].

2）教师方面：端正对通识课的态度，精心组织教学内容，合理设计教学过程，注重案例的选取并充分调动学生参与案例分析的积极性.要充分利用多媒体教学等技术手段，开展研究性的教学活动，加强课程的实践性环节.

3）学生方面：应重视通识课程的学习，提高通识课的学习兴趣.要学会自主构建知识体系的学习方法，通过自主建立学习目标，自主制定学习计划，自主开展学习活动和自主进行学习评价而努力成为社会真正需要的人才.

[1] 曾德军.大学通识教育课程设计与评价体系的研究[D].武汉：武汉大学,2004:1-2.

[2] 刘新燕,刘雁妮,杨智，等.构建新型顾客满意度指数模型——基于SCSB、ACSI、ECSI的分析[J].南开管理评论,2003(6): 52-56.

[3] 刘新燕，刘雁妮，杨智，等.顾客满意度指数(CSI)模型述评[J].当代财经,2003(6):57-60.

[4] 刘武，杨雪.中国高等教育顾客满意度指数模型的构建[J].公共管理学报,2007,4(1):84-88.

[5] 吴兆龙，丁晓.结构方程模型的理论、建立与应用[J].科技管理研究,2004(6):90-92.

[6] 亓莱滨.李克特量表的统计学分析与模糊综合评判[J].山东科学,2006,19(2):18-23.

[7] 哈斯巴根.高校课堂教学质量结构方程模型构建与应用——教师评价的视角[J].高校教育管理,2013,7(4):105-110.

[8] 王丽伟，吕洁，光明.结构方程模型在高校公选课学生满意度研究中的运用[J].统计与咨询,2011(1):36-37.

[9] 刘晓东,唐亚晖.结构方程模型在课程评价中的应用[J].统计与决策,2009(13):160-162.

[10] 邓慧杰.我国高校通识教育课程的教学优化研究[D].开封：河南大学,2011：47-50.

TheApplication of SEM in Evaluating General Courses

WANG Zhaozhi1,XIE Guozhong2,LIANG Shaojia3,DENG Shuangjiao1

(1.School of Chemistry and Chemical Engineering,Zhaoqing University,Zhaoqing,Guangdong 526061,China; 2.Experimental Middle School of Dinghu District,Zhaoqing,Guangdong 526070,China; 3.Guangli Junior High School of Dinghu District,Zhaoqing,Guangdong 526073,China)

In order to establish an authentic and reliable evaluation method of general courses,the structural equation model has been studied and on it the hypothesis model for students’evaluation on general courses in Zhaoqing University has been established.Under this model,six potential variables(including the desired teaching effects,perceived quality of the course and effect of classroom perception,perceptual learning results,satisfaction and loyalty etc.)and seventeen measurable variables as the evaluation factors are applied to analyze and verify the hypothesis.The results show that the fitting degree of the model is good,and all of the six research hypotheses are supported.Some suggestions are put forward to improve the teaching effect of general courses in universities.

general courses;structural equation;structural equation model

O242.1；G420

A

1009-8445（2017）02-0053-05

（责任编辑：张宝杰）

2016-11-1

王赵志（1974-），男，河南郑州人，肇庆学院化学化工学院副教授.