油管柱在套管中的屈曲行为试验研究

温后珍，闫兵洋，曹梦雨，王尊策，李仁峰，葛 朋(.东北石油大学 机械科学与工程学院，黑龙江 大庆 6338；.北京博纳电气有限公司，北京 008)

油管柱在套管中的屈曲行为试验研究

温后珍1，闫兵洋1，曹梦雨1，王尊策1，李仁峰1，葛 朋2
(1.东北石油大学 机械科学与工程学院，黑龙江 大庆 163318；2.北京博纳电气有限公司，北京 102208)

油管柱在套管中的屈曲行为对油气生产有重要影响。依据相似理论，采用1∶10的比例尺以缩小的油管、套管模型进行了3组试验，安装分别为：①油管和套管上下同心；②油管上部偏心2.5 mm；③油管上下都朝同一个方向偏心2.5 mm。每次试验时都在油管的一端连续施加轴向载荷，测试油管另一端的轴向载荷。分析不同条件下摩擦力的变化，研究结果表明：管柱受压屈曲会导致摩擦力增大；管柱相对套管的偏心对轴向力的分布影响很小；证明了管柱力学分析理论中轴向力计算时油管与套管同心的假设是合理的。

油管柱；屈曲；试验

油管柱(包括注水管柱、采油管柱、测试管柱、压裂管柱、钻柱等)在工作状态下的受力情况非常复杂，可能受到的力包括弯矩、拉伸力、压缩力、转矩、重力、与套管的摩擦力、管柱内外流体压力、热应力、与流体的粘滞摩阻等，使得油管柱产生复杂的变形。如果油管所受应力和变形过大，就会造成管柱及套管壁破损、封隔器坐封失效、管柱螺纹密封失效等结果。因此，有必要对油管柱的受力及变形开展研究。实际生产中的油管柱最长可达10 000 m，而直径为0.1 m左右，其长径比非常大。受限于空间及资金，难以在室内针对油井中的整个油管柱开展试验，研究受力与变形情况。对油管柱受力的研究主要采用理论分析计算[1-3]，而相关的试验研究比较少。文献[4]采用有机玻璃管作模拟井筒，用钢管作模拟管柱，对垂直井眼中管柱屈曲的发生、发展、恢复过程进行了模拟试验研究。文献[5]针对管柱屈曲的问题，采用弹簧在有机玻璃管中屈曲进行模拟试验。本文依据相似理论，以缩小的油管、套管模型在管柱力学试验台上开展油管柱的屈曲行为试验研究。

1 管柱力学试验模型的相似常数

依照相似第一定律可知，要以模型测试的结果来预测原型，必须使原型和模型的相似准则相等。油管柱在套管中屈曲，与轴向力Ft、管柱长度l、弹性模量E、截面惯性矩I、泊松比μv、套管对管柱的支反力Nq、摩擦因数μf、井眼半径减去管柱半径rc、力矩M、管柱位移u有关。选择力[F]和长度[L]作为基本量纲，采用矩阵法推导，可得8个相似准则：

(1)

以附下标m的变量表示模型的值，不附下标的变量表示原型的值。由相似理论可知，只要模型和原型的这8个相似准则相等，那么模型和原型的物理现象就是相似的，可以依据模型的值来预测原型。式(1)可写为：

(2)

令CF、Cl、CE、CI、Cv、CN、Cf、Cr、CM、Cu为轴向力Ft、管柱长度l、弹性模量E、截面惯性矩I、泊松比μv、套管对管柱的支反力Nq、摩擦因数μf、井眼半径减去管柱半径rc、力矩M、位移u的相似常数。

结合试验的实际情况，指定模型与真实管柱的几何比例为1∶10，即Cl=l/lm=10，模型管柱和套管的材料为钢材，与原型一样，因此弹性模量的相似常数CE=E/Em=1，泊松比的相似常数Cv及摩擦因数的相似常数Cf也都为1，将这些值代入式(2)可得：

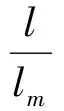
(3)

2 管柱力学试验台

设定套管长度为20 m，内径120 mm左右。测试油管长度为20 m，外径70 mm左右。依据几何比例，试验台上的套管长度为2 m，油管测试段长度为2 m，相应的油管外径7 mm左右，套管内径12 mm左右。以这几个尺寸为依据设计了管柱力学试验台，如图1所示。

该管柱力学试验台包括机架、工件夹持系统、控制与测试系统、加载系统。基于该试验台，可以对长2 m，直径4～13 mm的管柱在套管中的受力变形进行试验研究。可以在油管的一端施加拉压力、转矩，在中部施加弯矩，可以设定油管和套管的偏心，可以测出油管端部位移、拉压力和转矩。

a 实物

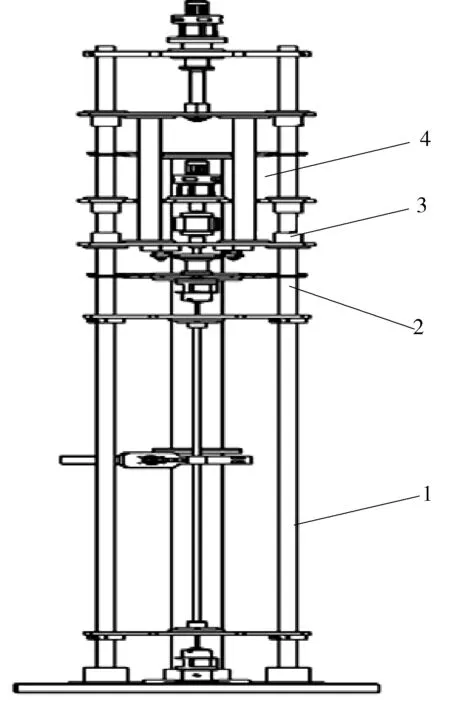
b 结构

3 试验对象及过程

在管柱力学试验台上开展油管柱受压屈曲后的轴向力测试。为模拟20 m长，外径70 mm，内径50 mm的油管柱在内径115 mm的套管中的力学行为，选择试验的管柱材料为45#钢，外径7 mm，内径5 mm，弹性模量为206 GPa。生产中使用的油管一般每根长度为10 m左右，20 m长的管柱应该由2根油管通过螺纹连接获得。管柱的屈曲行为主要取决于抗弯刚度EI，管柱长径比大，接头对管柱屈曲的力学行为影响不大。考虑到模型制作存在困难，本次试验使用一根2 m长的钢管来模拟20 m长的实际油管柱。套管为钢管，内径11.5 mm，长度2 m。安装好后如图1a所示。

将钢管和套管在试验机上安装好以后，进行了3组加载试验，试验的参数如表1所示。顶部载荷为连续加载0～-900 N(顶端加载为向上拉力时为正值、向下压力时为负值)。

表1 试验参数

4 试验结果

1) 油管和套管上下同心。

安装时油管与套管同心的测试结果如表2所示。

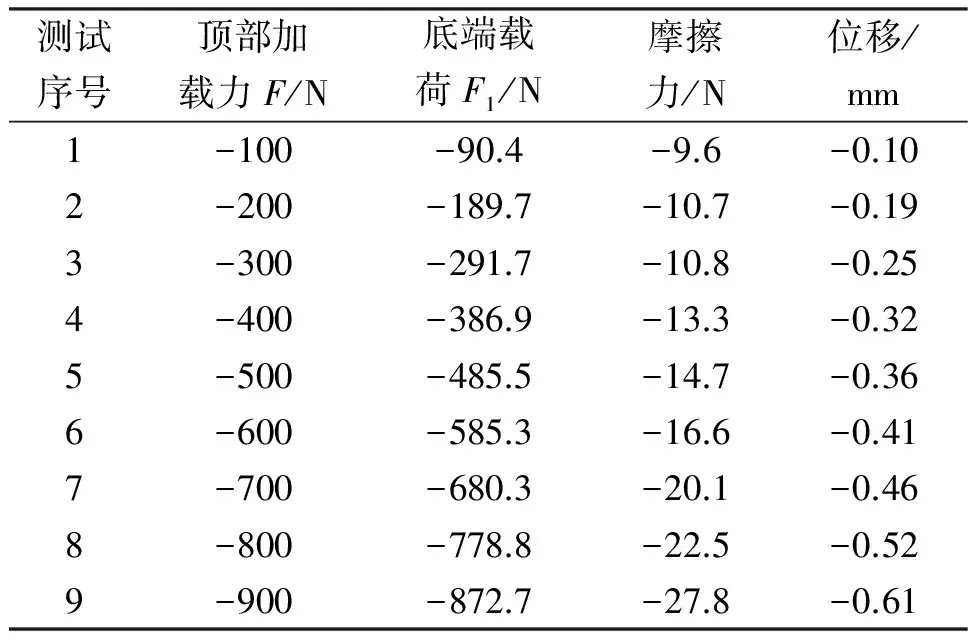
表2 管柱同心时油管柱屈曲试验结果(部分)

2) 油管顶部与套管偏心，下部同心。

安装时油管顶部与套管偏心2.5 mm，下部同心的测试结果如表3所示。

表3 管柱顶端偏心时油管柱屈曲试验结果(部分)

3) 油管与套管上下朝同一侧偏心。

安装时油管与套管上下朝同一侧偏心2.5 mm的测试结果如表4所示。

表4 管柱上下端向同一侧偏心时油管柱屈曲试验结果(部分)

表4(续)

由式(3)可知，模型上测得的力映射到原型上应该放大100倍，而位移应该放大10倍。因此表2、表3和表4即变为表5、表6和表7。

表5 同心状态真实油管柱屈曲的轴向力及摩擦力

表6 顶部偏心真实油管柱屈曲的轴向力及摩擦力

表7 上下同时偏心真实油管柱屈曲的轴向力及摩擦力

5 结果分析

从试验结果来看，随着轴向压缩载荷的增加，传递到管柱底端的轴向力也跟着增加，顶部载荷值与底部载荷值有一个差，并且这个差值随着载荷的增大越来越大。这是由于油管柱随着受到的压力增大，屈曲越来越严重，与套管的接触力越来越大，随之摩擦力也越来越大。因此，由于摩擦力造成的轴力损失也越来越大。

将这3种状态下油管柱所受摩擦力随顶部载荷的变化曲线放到同一张图上进行对比，如图2所示，顶部偏心管柱和上下齐偏心管柱由于与套管接触，在微小载荷时即有摩擦力的存在；而上下同心管柱在顶部载荷小于2 000 N时摩擦力为0，这是由于油管柱没有屈曲，与套管没有接触。但顶部载荷上升到3 000 N左右时，摩擦力都快速上升，这3条曲线有一部分重合。这说明3 000 N是管柱屈曲的临界载荷，且管柱与套管的偏心与否对屈曲临界载荷影响很小。越过屈曲临界值后，这3种安装状态下摩擦力随顶部载荷的增大而增大，变化趋势相同，如图2所示。3种状态下摩擦力最大差为700 N，在图2上看似乎很大，但对于几万牛的轴向载荷的而言，这个差对轴向载荷的影响小到可以忽略不计。

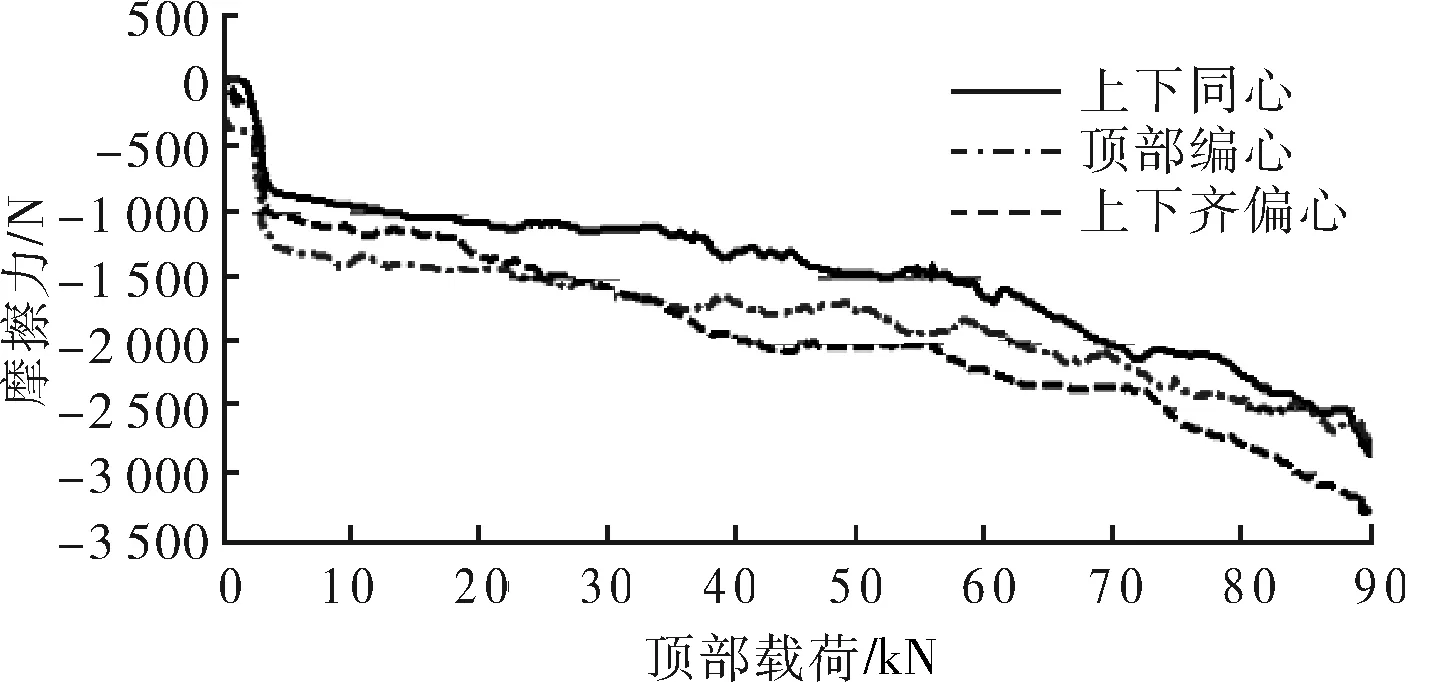
图2 油管和套管 3种安装位置的摩擦力对比

图3为3种安装位置下底部载荷与顶部加载的关系，图中列出了顶部载荷为-10 000、-20 000、…、-90 000 N时底部载荷的值。图中这3条曲线基本重合。在顶部载荷为44 200 N时底部载荷差取得最大值，为700 N。此时上下同心管柱底部载荷为42 900 N，上下齐偏心管柱底部载荷42 200 N，上偏心管柱底部载荷42 500 N，以同心状态管柱的轴向力来预测管柱的轴向力，最大误差为1.6%。由此可知，初始状态下管柱相对套管的偏心，对于管柱轴向载荷分布的影响很小。在管柱力学分析理论中，对管柱轴向力计算时假设在初始状态管柱与套管中心轴线重合，忽略管柱初始状态相对套管的径向位移。本次试验的结果证明这个假设是合理的。

图3 油管和套管三种安装位置的底部载荷与顶部加载的关系

6 结论

1) 油管柱在套管中受压，随着压力的增大，油管柱会屈曲，与套管产生接触。压力越大，屈曲越严重，摩擦阻力也随之增大。

2) 初始状态油管柱相对套管偏心时，对于油管柱屈曲临界载荷及轴向载荷分布的影响很小。

3) 本次试验的结果证明管柱力学理论中忽略管柱初始状态相对套管的径向位移，假设管柱和套管中心线重合的做法是正确的。

[1] 刘清友，何玉发.深井注入管柱力学行为及应用[M].北京：科学出版社，2013.

[2] 刘凤梧，徐秉业，高德利.封隔器对油管螺旋屈曲的影响分析[J].清华大学学报(自然科学版)，1999，39(8)：104-107.

[3] 高德利，刘凤梧，徐秉业.油气井管柱的屈曲行为研究[J].自然科学进展，2001，11(9)；976-980.

[4] 高德利，高宝奎，冯光通.垂直井眼中管柱屈曲与摩阻模拟实验研究[C]//高德利，张玉卓，王家祥.地下钻掘采工程不稳定理论与控制技术：中国科学技术协会第46次“青年科学家论坛”论文集.北京：中国科学技术出版社，1999：217-225.

[5] 王宇，高国华.斜直井眼中管柱变形参数仿真实验[J].石油学报，2003，24(3)：94-97.

[6] 吕英民，帅建.水平井中钻柱的临界载荷[J].石油钻采工艺，1992，14(4)：1-6.

[7] 曾宪平.油管柱的受力与变形[J].石油钻采工艺，1981，3(3)：39-54.

[8] 江汉采油工艺研究所.封隔器理论及应用基础[M].北京：石油工业出版社，1983：142-248.

[9] 李子丰，马兴瑞，黄文虎.水平管中受压扭细长圆杆(管)的几何非线性弯曲[J].力学与实践，1994，16(3)：16-18.

[10] 于永南，韩志勇.斜直井眼中钻柱侧向屈曲研究[J].石油大学学报(自然科学版)，1997，21(3)：65-67.

Experimental Study of Buckling Behavior of Tubing String in the Casing

WEN Houzhen1，YAN Bingyang1，CAO Mengyu1，WANG Zunce1，LI Renfeng1，GE Peng2
(1.MechanicalScienceandEngineeringInstitute，NortheastPetroleumUniversity，Daqing163318，China；2.BeijingBannerElectricCo.，Beijing102208，China)

The buckling behavior of tubing string in the casing is the key problem in petroleum engineering，which has important influence on oil and gas production.In this paper，based on the similarity theory，using the 1∶10 scale to shrink tubing and casing model for three groups of test，one is installed when the tubing and casing concentric.The second is the upper eccentric 2.5 mm.Eccentric top and bottom tubes are all in the same direction in three is 2.5 mm.Each test continuous apply axial load at the end of the tubing，test the axial load at the other end of tubing.The change of friction under different conditions is analyzed，the results show that the compression of pipe string buckling causes friction increases.The relative casing string eccentric little impact on the distribution of axial force.For the tubular mechanical theory of axial force calculation，it proved the assumption that the tubing is concentric with the casing is reasonable.

tubing string；buckling；testing

2016-11-23

国家青年科学基金(11402051)；东北石油大学研究生创新科研项目(YJSCX2016-021NEPU )

温后珍(1982)，男，硕士，副教授，研究方向为石油流体机械，E-mail：wenhouzhen@163.com。

1001-3482(2017)03-0036-05

TE931.207

A

10.3969/j.issn.1001-3482.2017.03.008