变指数空间下局部权性质

王骏

(哈尔滨师范大学)

变指数空间下局部权性质

王骏

(哈尔滨师范大学)

主要研究在变指数空间中局部Ap(·)权性质.证明中的关键环节是通过分割区域来构造局部权与权之间的联系.

变指数空间;局部Ap(·)权

0 引言

设f∈Lloc(Rn)，x∈Rn.令Q是包含x的方体，称为f定义在Rn上的Hardy－Littlewood极大算子，Q表示边和面都平行于坐标轴的方体.

设w≠0，w∈Lloc(Rn)，1≤p＜∞.若存在常数C＞0，使得对所有的Q方体都有

则称w∈Ap.若存在常数C＞0，使得对所有的方体Q都有

2010年，Lin和Stempak［1］定义了Rn，n≥1中的局部Ap权和局部Hardy－Littlewood极大算子，定义如下:

对任意的x∈Rn，记‖x‖ =max{|x1|，…，|xn|}，x=(x1，…，xn)，Q={y∈Rn:‖x－y‖≤r}，表示中心在点x且其半径长为r＞0的方体(若n=1，则方体为闭区间).

设k＞0，记Ok(y)为中心在点y且其半径r≤k‖y‖的方体的全体，并定义

1 预备知识

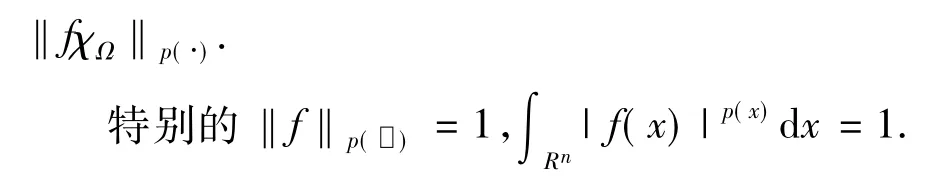
引理1.6［4］给定集合G，p(·):Rn→［1，∞)，对任意t≥1，存在常数C=C(t，C0)和p∞对f≤1，有I1=±［k－t，k－t+1］.

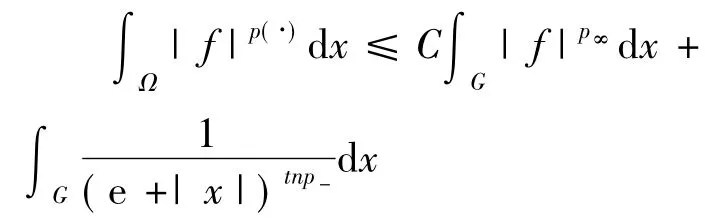
其中p(·)和p∞可互换.

设0＜k＜1，现将Rn分成一些矩体的全体，这些矩体无限靠近远点但不包含坐标原点有，具体做法如下:将Rn分成I1=±［k－1，k－t+1］

其中对t∈Z，分别称其为第一型，第二型，第三型区间(其中 －［a，b］表示区间［－a，－b］).

若G为第一类，定义G″为沿坐标距原点最远的包含G'的最小方体.若G为第二类的，定义为沿坐标轴距原点最远的包含的最小方体.

2 主要结果及证明

现将v对称延拓到Q0上定义为vQ，显然其在Q与v相等，再通过d个通过中心x包含Q的一个超平面对称性将vQ扩张成Rn上的函数.

vQ是以2r为周期的具有周期性的函数.

定理2.2给定p(·)→［1，∞)，Q为Rn中的方体，v为此方体上的函数

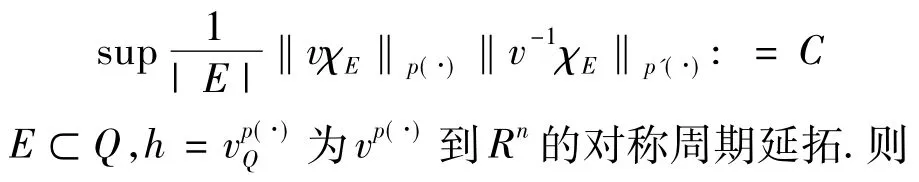
由引理1.5上式右边第一个积分可等于1.由引理1.5可将w从Q上延拓到Rn上，记为hQ(·)= vQ(·)p(·)且vQ(·)∈Ap1(·)对于右边第二个积分可取t足够大使得其值小于1.记方体Qk= Q(0.2k)并由引理1.5得

同样可使上式右边第二项小于1/2，可得‖vQχE‖p(·)≤ChQ(Q)1/p∞.

并结合引理2.4得

由前述过程可知

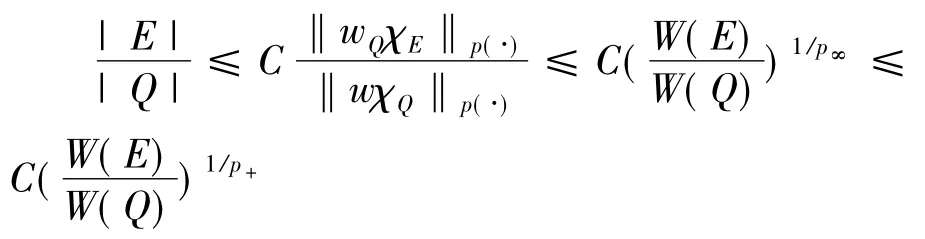
推论2.7给定p(·):Rn→［1，∞).若1＜p－＜p+＜∞并p(·)满足log－Hölder连续条件，且w－=ess inf|w|＞0对任意，存在方体Q∈Ok及可测集使得‖wχE‖p(·)≥1，有

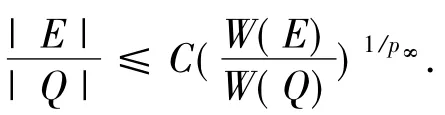
推论2.8给定p(·):Rn→［1，∞).若1＜p－＜p+＜∞并p(·)满足log－Hölder连续条件，且w－=ess inf|w|＞0对任意，存在方体Q∈Ok使得‖wχQ‖p(·)≥1，有‖wχQ‖p(·)≈W(Q)1/p∞.

［1］Lin C C，Stempak K.Local Hardy－Littlewood Maximal Operator Math Ann，2010，348(4):797－813.

［2］Orliz W.Uber konjugierte Exponentenfolgen.Studia，1931 (3):200－211.

［3］Kovacik O，Rakosnik J.A on spaces an Czechoslovak.Math J，1991，41(4):592－618.

［4］Cruz－Uribe，Fiorenza D A，Neugebauer C J.Weighted Norm Inequalities for the Maximal Operator on Variable Lebesgue Spaces.J Math Anal Appl，2012，394:744－760.

［5］Hardy G H，Littlewood J E.A Maximal Theorem with Function Theoretic.Acta Math，1930(54):81－116.

Local Weigts in Variable Lebsgue Spaces

Wang Jun
(Harbin Normal University)

In this paper，the the local weight in variable lebesgue space is studied.The relationship between the global and local Ap(·)weight functions is established.

Varable Lebesgue Spaces;Local weights

O17

:A

:1000－5617(2017)01－0013－05

(责任编辑:季春阳)

2016－11－12