考虑磁场分布的精密磁致伸缩驱动器的涡流损耗特性研究
刘慧芳,王汉玉,杨国哲,张 禹
(沈阳工业大学机械工程学院,沈阳 110870)
考虑磁场分布的精密磁致伸缩驱动器的涡流损耗特性研究
刘慧芳*,王汉玉,杨国哲,张 禹
(沈阳工业大学机械工程学院,沈阳 110870)
为了准确的计算棒状超磁致伸缩材料GMM(Giant Magnetostrictive Materials)的涡流损耗特性、提高控制超磁致伸缩执行器的位移精度,建立了考虑集肤效应的GMM棒涡流损耗模型。首先从麦克斯韦方程入手,推导出了棒状GMM的传统涡流损耗公式,接着讨论了集肤效应对于GMM棒内部磁场分布的影响,建立了考虑集肤效-应的棒状GMM涡流损耗公式,最后通过comsol多物理场有限元数值分析法及实验分析了GMA的温度特性。通过与传统涡流损耗对比可知,在低频时两种方法得到的结果基本一致,而在中高频时考虑集肤效应的涡流损耗公式可以更加准确的计算棒状GMM的涡流损耗。研究成果对提高GMA的控制精度、推进涡流损耗的研究具有重要意义。
磁致伸缩执行器;涡流损耗;温度特性;涡流效应
超磁致伸缩材料GMM(Giant Magnetostrictive Material)作为一种新型功能材料,其具有磁致伸缩系数大、工作频率宽、响应速度快、能量密度高和磁-机转换效率高等优异特性[1-3]。超磁致伸缩执行器GMA(Giant Magnetostrictive Actuator)是以棒状GMM为核心驱动元件的微位移驱动装置。凭借超GMM具有的优异特性,GMA在声呐,振动控制系统中已经得到了广泛的应用,并且在精密与超精密加工、流体机械等工程领域显示出了良好的应用前景[4-6]。然而,GMM的电阻率非常小,通常约为60×10-8Ω·m,因此在时变磁场驱动下GMM内部会产生感应电流,即涡流[7-8]。涡流的存在将会影响线圈所提供的激励磁场,并且改变材料内部磁场分布的均匀性。许多实验证明GMA的输出具有明显的磁滞特性[9-10],磁滞及涡流的存在导致执行器的输出特性具有非线性。相关研究表明由涡流引起的损耗不仅影响超磁致伸缩材料的磁-机转换效率,还会改变GMM的温度特性[11-12]。目前关于GMA的涡流损耗以及温度特性的研究尚处于初步探索阶段,例如,李立毅,严柏平等人分析了磁化过程中磁弹性力、频率对GMA磁场以及温升特性的影响[13];Kyung-HwanHwang和Sung-Ryul Kim通过实验分析了欧姆热对于执行器输出特性的影响[12];Soheil Talebian在传统涡流损耗的基础上提出了超涡流损耗的概念[14];Engdahl提出了圆柱状GMM涡流损耗的数值方程[15]。虽然上述研究可在一定假设前提下准确描述某一低频段内的GMM涡流损耗及温度特性,但其仅能够对理想状态下GMM的磁场分布及能量损耗进行分析。目前,关于涡流引起的GMM内部磁场分布不均匀特性对涡流损耗影响规律以及GMA温度分布特性的研究较少。
本文基于麦克斯韦方程和Jiles-Atherton模型研究了集肤效应、磁滞对于涡流损耗特性的影响,建立了考虑集肤效应及磁滞的GMM涡流损耗数学模型;此外,分析了驱动频率对GMM涡流损耗及执行器温度特性的影响。研究结果为推进超磁致伸缩执行器的精密控制及涡流损耗的研究提供了一种理论基础。

1.碟形弹簧,2.传递轴,3.不锈钢上盖,4.预紧螺母,5.螺栓,6.紧固螺母,7.不锈钢中盖,8.上导磁片,9.纯铁套筒,10.不锈钢套筒,11.上导磁块,12.线圈骨架,13.GMM棒,14.下导磁块,15.防磁钢圈,16.下导磁片,17.不锈钢底座,18.线圈图1 超磁致伸缩微位移执行器结构图
1 执行器的工作原理
如图1所示,超磁致伸缩微位移执行器主要由预紧螺栓、传递轴、上下导磁滑块、GMM棒、线圈、线圈骨架、上下端盖和壳体等组成。通过调节预紧螺栓对GMM棒施加预紧力,使超磁致伸缩微位移执行器达到最佳工作状态。当线圈中通入电流后,GMM棒在线圈产生的磁场作用下伸长或缩短。GMM棒的下端固定,GMM棒的长度变化由上端推动上导磁滑块、传递轴,实现位移和力的输出。在GMM内部存在着数量众多的磁畴,磁场的作用下其内部磁畴体积增大引起磁壁移动,GMM材料伸长。然而时变磁场的作用下,在磁畴发生旋转、移动的同时在其内部会产生涡流,涡流的存在会削弱激励磁场的大小,降低GMM的磁机转换效率,、影响GMA输出位移的精确性。
2 GMM棒的磁滞模型及涡流损耗理论
2.1 GMM棒的磁化模型
在理想状态下,GMM内部的畴壁移动和磁畴转动是完全可逆的即不存在磁滞,在Jiles-Atherton磁化强度磁滞模型中,材料的无磁滞磁化强度Man和有效磁场He分别表示为[1,7]:
(1)
He=H+αMan
(2)
式中:α为畴壁相互作用系数,a为形状系数,Ms为饱和磁化强度,H为磁场强度。
但是,在实际的磁化过程中由于存在能量损失使得材料内部的畴壁移动和磁畴转动是不完全可逆的,即可逆磁化强度Mre和不可逆磁化强度Mirr同时存在。此时材料内部的磁化强度M、可逆磁化强度Mre和不可逆磁化强度Mirr可以分别表示为:
M=Mre+Man
(3)
(4)
Mre=c(Man-Mirr)
(5)
方程中k为不可逆损耗系数,β为形状因子,c为可逆系数。
根据磁学理论磁感应强度B可以写为:
B=μ0(M+H)
(6)
假设线圈内部磁场分布均匀,当线圈通入电流为I,线圈内部的磁场强度为:
H=NI/LC
(7)
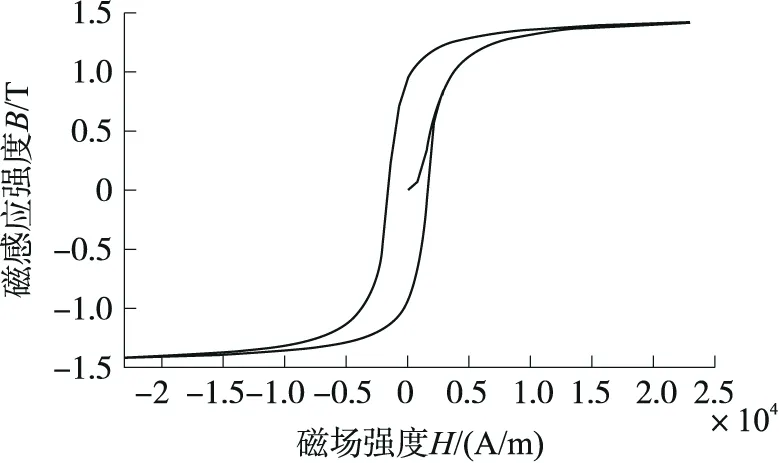
图2 GMM棒的磁滞曲线
式(1)~式(7)所涉及的模型参数见表1,当线圈通入电流为I=2sin(2πft),此时GMM棒的静态磁滞曲线如图2所示,当磁场强度达到15 kA/m时GMM材料达到磁化饱和状态。

表1 模型参数表
2.2 GMM棒的涡流损耗理论
GMM棒在时变磁场下作用时,根据麦克斯韦定律可以得到:
×E=-
(8)
J=σE
(9)
式中:E为电场强度,B为磁感应强度,J为涡电流密度,σ为GMM的电导率。在如图3所示的圆柱坐标系下,由于圆柱的对称性方程(8)又可以改写为[14]:
(10)

图3 圆柱坐标系下GMM棒磁场分布的数学模型
因为B=B0ejωt,同时方程(10)对半径r进行积分可得到所圆柱坐标系下GMM棒的电场强度公式:

(11)
根据方程(8)和(11)可以得到任意时间t和半径r的涡流损失
(12)
方程(12)对半径r进行积分即可得到径向截面内任意时刻的传统涡流损耗:
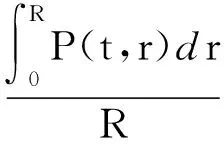
(13)
方程中r为GMM棒的半径。式(11)~式(13)即为GMM的古典涡流损耗数学模型,其中GMM内部的磁场感应强度B的值由磁化模型中的式(6)确定。
假设GMM材料内部的磁感应强度B均匀分布,当线圈中通入电流I=1A,2A,3A,4A,利用上述古典涡流损耗理论计算不同频率下考虑磁滞的GMM棒涡流损耗,结果如图4所示,随着频率的增加GMM棒的涡流损耗呈现出近似指数形式的增加。

图4 不同频率下GMM棒的涡流损耗
然而,由于GMM电阻率非常小,因此在时变磁场激励下,其内部将产生感应电流即涡流。涡流将产生磁场,且其方向与线圈激励磁场方向相反,在GMM棒中心位置处的涡流反向磁场最强,形成集肤效应[16]。对于棒状的磁性材料,有效磁场能到达材料的径向深度,即集肤深度用δ表示:
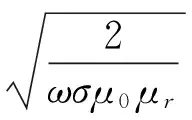
(14)
式中:μ0为真空磁导率;μr为材料的相对磁导率。

图5 集肤深度曲线图
集肤深度与频率的关系如图5所示。结果表明随着频率的增加集肤深度减小,因此,在某个高频范围内GMM中的磁场区域将不能完全被渗透。为了描述GMM的磁场渗透深度对涡流损耗的影响,将式(13)改写为:

(15)
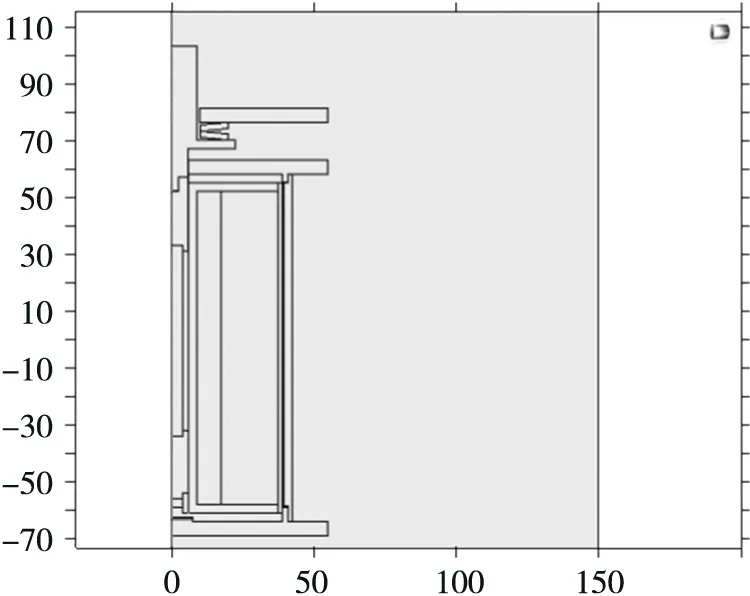
式中:r0为有效磁场未渗透区域的半径,当δ≥R时r0恒为0;当δ 涡流引起的集肤效应将会减小GMM内的实际磁场强度,造成其内部磁场分布不均。根据麦克斯韦方程,在圆柱坐标系下GMM棒的径向磁场分布方程为[16]: (16) 式中:k2=jωμrσ,ω为时变磁场的角频率,μr为GMM的相对磁导率,σ为GMM的电导率。式(18)为零阶修改贝塞尔方程,其解为I0(kr)。当线圈提供H0ejωt的磁场强度时,半径为R的GMM棒内部r处的磁场强度可表示为 (17) 当激励磁场的角频率ω较大时,|kr|→∞,由贝塞尔函数渐进公式: (18) 可以得出 (19) (20) 式中:r0为有效磁场未渗透区域的半径。 因此,当考虑GMM内部磁滞和集肤效应对涡流损耗的影响时,首先根据激励频率利用集肤深度式(14)计算集肤深度,接着利用式(20)计算平均磁场强度,并将其代入式(10)~式(13)计算材料内部考虑磁滞的磁感应强度B,最后利用式(15)计算GMM棒的涡流损耗。 取GMM棒的半径R=4 mm、L=70 mm,当磁场驱动频率从100线性增加到1 000时各频率下的传统涡流损耗与考虑涡流效应的涡流损耗对比如图6所示。 图6 传统涡流损耗与考虑涡流效应的涡流损耗对比图 从图6可以看出当激励频率小于300 Hz两种计算方法的涡流损耗相同,结合图5可知当激励频率小于300 Hz时,整个GMM棒被磁场完全渗透,此时涡流效应对于GMM内部磁场分布的影响很微小。随着激励频率的增加两种损耗曲线开始出现差异,由于当频率增加时涡流产生的集肤效应增强,在GMM棒内部开始出现未被磁场渗透区域,此区域不会产生涡流损耗。而传统的涡流计算方法将整个GMM棒内部的磁场看做是均匀分布所计算的损耗包含为被磁场渗透区域,因此计算结果要比实际损耗值大。而本文中提出的涡流损耗计算考虑了磁滞及涡流效应相比于传统的损耗计算方法结果更为准确,对推动超磁致伸缩执行器的准确控制具有重要意义。 在执行器工作过程中GMM产生的涡流、磁滞损耗以及驱动线圈产生的焦耳热都会引起执行器的温度分布变化,温度是涡流损耗的宏观表征可以体现GMM涡流损耗的特点及规律。关研究表明GMM具有非常敏感的温度特性,温度的变化将严重影响执行器的机械输出特性。因此准确的描述执行器内部温度分布规律对于执行器冷却系统的设计及精确控制具有重要意义。 图7 执行器有限元模型 由于GMM具有较强的非线性,执行器的温度场与电磁场间存在复杂的耦合关系。因此采用有限元分析法和实验分别对其温度特性进行分析,其中实验部分温度通过贴在GMM棒中间位置的PT100传感器芯片获得。建立的执行器的有限元分析模型如图7所示。 由式(11)~式(13)以及图6可知GMM的涡流损耗与频率具有极大的相关性,在高频下其损耗随着驱动的频率的增加趋势呈现近似指数形式。材料的温度特性直接体现了其涡流损耗特点,如图8所示。GMM棒在不同频率下的温度特性可以看出随着频率的升高由于GMM棒的涡流损耗逐渐增大导致GMM棒温升速度明显加快,并且仿真数据与实验数据一致性较好,此结果与图6所示的涡流损耗规律一致。 图8 不同频率下磁致伸缩材料的温升特性 在GMA中存在磁致伸缩材料产生的涡流、磁滞损耗以及驱动线圈产生的焦耳热两种损耗热源,虽然涡流、磁滞损耗和线圈的电阻损耗都属于电磁损耗都,但其损耗带来的温升特性却是不同的,相对应的冷却措施也不同。因此,为了使冷却效果达到最佳,研究执行器在不同频率下的温度特性对于冷却系统的设计具有指导作用。将模型的线圈区域通入2 A的交流激励,工作60 s,执行器不同频率下线圈区域及GMM棒的仿真及实验温度特性如图9所示,当驱动频率在200 Hz以下时由图9可以看出线圈的温度要高于GMM棒的温度,此时线圈为执行器的主要热源;当激励频率大于200 Hz后GMM棒的温度要高于线圈区域,GMM棒的涡流、磁滞损耗为执行器的主要热源。 图9 不同频率下线圈温度与GMM棒温度对比图 建立了考虑涡流效应的GMM棒涡流损耗数学模型,通过与传统涡流损耗对比可知,在中高频下本文所建立涡流损耗模型的计算结果更加准确;通过有限元分析方法分析了不同频率下GMA的温度分布特性及GMA的主要热源类型,在200 Hz以下线圈为GMA的主要热源,200 Hz以上GMM棒的涡流、磁滞损耗为执行器的主要热源。研究结果对于执行器的精确控制及冷却系统的设计具有重要意义。 [1] 贾振元,杨兴,郭东明,等. 超磁致伸缩材料微位移执行器的设计理论及方法[J]. 机械工程学报,2001,11(37):46-49. [2] Zhou M,Zheng J,Zhou H. Active Vibration Control of Nonlinear Giant Magnetostrictive Actuator[J]. Smart Mater Struct,2006(15):792-798. [3] Wang Tianzhong,Zhou Youhe. Nonlinear Dynamic Model with Multi-Fields Coupling Effects for Giant Magnetostrictive Actuator[J]. International Journal of Solids and Structures,2013,50:2970-2979. [4] Xu Q. Bust Impedance Control of a Compliant Microgripper for High Speed,Position/Force Regulation[J]. IEEE Trans Ind Electron,2015,62(2):1201-1209. [5] Yang Z,He Z,Li D,et al. Direct Drive Servo Valve Based on Magnetostrictive Actuator:Multi-Coupled Modeling and Its Compound Control Strategy[J]. Sensor Actuators A,Phys,2015,235:119-130. [6] 刘慧芳,赵俊杰,王文国,等. 考汽车燃油喷射系统用磁致伸缩驱动构件的建模与特性研究[J]. 传感技术学报,2016,29(12):1797-1803. [7] Jiles D C. Modeling the Effects of Eddy Current Losee on Frequency Dependent Hysteresis in Electrically Conducting Media[J]. EEE Transcations on Magnetics,1994,(30)6:4326-4328. [8] 陶孟伦,陈定方,卢全国,等. 超磁致伸缩材料动态涡流损耗模型及实验分析[J]. 机械工程学报,2012,7(13):146-151. [9] Xu Ao,Pei Yongmao,Ai Shigang,et al. An Energy-Based Dynamic Loss Hysteresis Model for Giant Magnetostrictive Materials[J]. International Journal of Solids and Structures,2013,50:627-679. [10] ZhengJiaju,Cao Shuying,Wang Hongli,et al. Modeling of Magnetochanical Effect Behaviors in a Giant Magnetostrictive Device under Compressive Stress[J]. Sensors andActuators A,2008,14:204-214. [11] Sergey E Zirkaa,Yury I Moroza,Moses A J,et al. Volution of the Loss Components in Ferromagnetic Laminations with Induction Level and Frequency[J]. Journal of Magnetism and Magnetic Materials,2008,320:e1039-e1043. [12] Kyung-Hwan Wang,Sung-Ryul Kim,Jae-Hak Lee,et al. Design of a Magnetostrictive Actuator Considering Magnetic Bias and Ohmic Heat[J]. International Journal of Applied Electromagnetics and Mechanics,2014,45:867-871. [13] 李立毅,严柏平,张成明. 驱动频率对超磁致伸缩制动器的损耗和温升特性的影响[J]. 中国电机工程学报,2011,31(18):124-129. [14] Soheil Talebian,Yousef Hojjat,Mojtaba Ghodsi,et al. Study on Classical and Excess Eddy Currents Losses of Terfenol-D[J]. Journal of Magnetism and Magnetic Materials,2015,388:150-159. [15] Engdahl G.Hand Book of Giant Magnetostrictive Materials[M]. Academic Press,USA,2000. [16] 贾振元,郭东明. 超磁致伸缩材料微位移执行器原理与应用[M]. 北京:科学出版社,2008. Study on Eddy Current Loss Characteristics of Precision Giant Magnetostrictive Actuator Considering Magnetic Field Eddy LIU Huifang*,WANG Hanyu,YANG Guozhe,ZHANG Yu (School of Mechanical Engineering,Shengyang University of Technology,Shengyang 110870,China) In order to accurately calculate eddy current loss of the rod-shaped giant magnetostrictive material,improve the giant magnetostrictive actuator control accuracy of displacement,established a eddy current loss model of rod GMM that considering the skin effect.Firstly,deduced the traditional eddy current loss of rod-shaped GMM,then discussed the influence of the skin effect for the inside magnetic field distribution of GMM rod,finally analyzed the temperature characteristics of GMA throught the comsol multiphysics finite element numerical analysis method and experiment.Compared with traditional eddy current loss,under low frequency the two methods has same result,but under high frequency the new model can be more accurately calculate the eddy current loss of rod-shaped GMM.The research result has a great significance for improving the control precision and advancing the study of eddy current loss of GMA. giant magnetostrictive actuator;eddy current loss;temperature characteristics;eddy current effect 刘慧芳(1983-),女,辽宁朝阳人,博士,硕士生导师,2012年于大连理工大学获得博士学位,现为沈阳工业大学机械电子工程专业教师、机械工程流动站博士后,主要从事功能材料精密驱动与控制技术研究,hfliu@sut.edu.cn; 王汉玉(1991-),男,辽宁辽阳人,现为沈阳工业大学机械工程学院硕士研究生,主要从事磁致伸缩精密驱动技术研究,18802408921@163.com。 项目来源:国家自然科学基金项目(51305277);教育部博士点科研基金项目(20132102120007);沈阳市科技计划项目(F15-199-1-14);中国博士后科学基金特别项目(2014T70261) 2016-10-13 修改日期:2017-02-17 TP393 A 1004-1699(2017)06-0814-06 C:7230 10.3969/j.issn.1004-1699.2017.06.002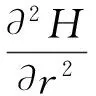
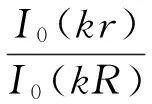




3 GMA的损耗温度特性分析


4 结论



