多智能体编队在时延约束下的动态跟踪控制
戴国忠,王怀龙
(中国人民解放军91655部队,北京 100036)
多智能体编队在时延约束下的动态跟踪控制
戴国忠,王怀龙
(中国人民解放军91655部队,北京 100036)
针对时延约束下多智能体编队的动态跟踪问题,提出了一种与模型无关的控制算法,并运用实用稳定性理论、图论和矩阵分析等工具,实现了多跟随者在时延影响的有向通信图下对单动态领航者的实用跟踪。基于Matlab的线性矩阵不等式(Linear Matrix Inequality, LMI)工具箱,以三自由度(Three Degree of Freedom, 3-DOF)的无人水下航行器(Unmanned Underwater Vehicles, UUV)进行数值仿真实验,可证明算法的正确性。
多智能体编队;动态跟踪;与模型无关;时延;UUV
多智能体编队的协同控制可以分为无领航者[1]和有领航者[2]两种类型。无领航者的协同网络中,所有智能体的地位是相同的。它主要运用于多个智能体的集结或者蜂拥等控制目标[3]。有领航者的多智能体编队重点研究有期望的或特定的同步目标的实际应用。当前,一般考虑领航者的参考轨迹和速度,也就是对领航者运动状态的跟踪[4]。一方面,从控制器来归类,关于多智能体协同控制的研究主要集中在与模型相关控制器的同步[5],这类研究引入了航行体动力学补偿项或者航行体动力学参数线性化矩阵,控制器的结构较为复杂。如何设计结构比较简单的控制器,比如与智能体模型无关的控制器,是需要解决的一个关键问题。另一方面,要增加单次传输的比特数,就会加重通信负担,使得信道拥塞,造成通信时延。时延[6]使得智能体获取近邻个体的信息相对滞后。如何利用时延信息实现多智能体协同也是一个具有重要现实意义的问题。
本文针对存在时延的有向通信网络,基于图论、矩阵理论和实用稳定性理论,设计了一种与模型无关的控制器,研究了多跟随者对单动态领航者的跟踪控制。研究结果表明,多跟随者可实现对单动态领航者的实用跟踪。3个3-DOF的UUV作为跟随者进行数值仿真实验,也验证了算法的正确性。
1 基础知识
考虑n个跟随者,第i个的动力学模型可用拉格朗日方程表示为
(1)
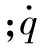
首先,提出如下与模型无关的控制器
i=1, 2,…,n
(2)

假定多跟随者之间时钟同步,且具备记忆能力,可根据自身需要获取其历史信息。那么,对于存在时延的有向通信网络,式(2)可改写为
(3)
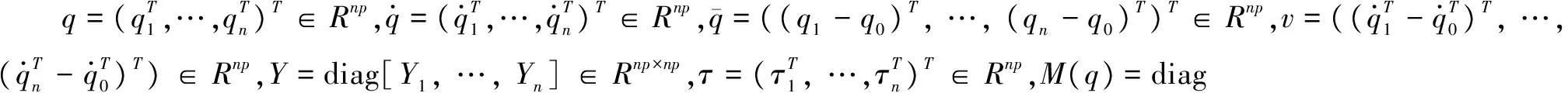

(4)

(5)
τ=-(HA⊗IP)e1(t-d(t))-Y(HB⊗IP)e2(t-d(t))
(6)
根据文献[8]的研究,提出实用跟踪的概念。
e∈Bδ={e1,e2| ‖e1‖2+‖e2‖2<δ2}
(7)
那么,多智能体实现了实用跟踪。

2 理论结果
基于文献[9]的研究,式(5)和(6)可构造误差系统

(8)
式中,

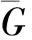

证明 考虑如下Lyapunov-Krasovskii函数
V=V1+V2
(9)
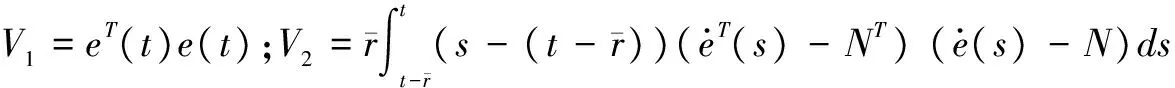
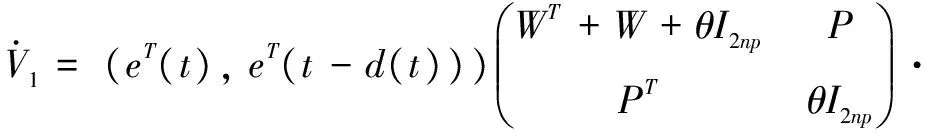
(e(t)-e(t-d(t)))T(e(t)-e(t-d(t)))+

(11)
进一步地
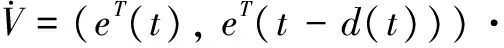
(12)
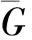
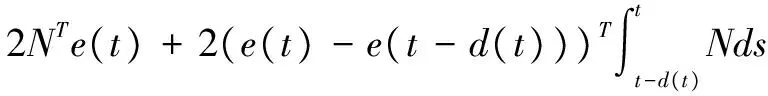
(13)
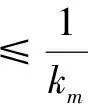
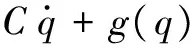
(14)
式(13)改写为

(15)
通过定义1的实用跟踪概念,给定δ>0,如果e(t)和e(t-d(t))都在球体Bδ的外部,式(15)可改写为
(16)

(17)
即多跟随者完成了对单动态领航者的实用跟踪。
3 数值仿真实验
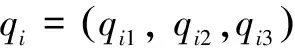

图1 跟随者和领航者的拓扑图
UUV的基本参数和初始状态为
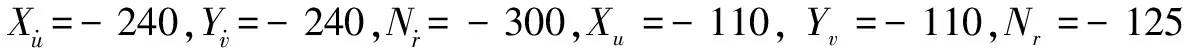
图2 跟随者和领航者广义位置第一自由度的变化轨迹

图3 跟随者和领航者广义位置第二自由度的变化轨迹

图4 跟随者和领航者广义位置第三自由度的变化轨迹

图5 跟随者和领航者广义位置第一自由度的误差轨迹
图6~8则为3个跟随者和单领航者的广义速度变化轨迹,可以知道:3个跟随者的速度随着领航者速度的变化而有小偏差地跟踪到领航者的速度。值得注意的是,虽然跟随者广义速度第一自由度的初始值较大,但是仍然可以较快地跟踪到领航者的速度,控制性能较好。进一步地,通过图9的广义速度第一自由度误差轨迹,易知跟随者的广义速度能很好地跟踪到领航者的广义速度,控制精度较高。综上,跟随者可实现对单领航者较小误差值的实用跟踪。

图6 跟随者和领航者广义速度第一自由度的变化轨迹

图7 跟随者和领航者广义速度第二自由度的变化轨迹

图8 跟随者和领航者广义速度第三自由度的变化轨迹
图9 跟随者和领航者广义速度第一自由度的误差轨迹
4 结束语
本文研究了多跟随者在时延影响下对单动态领航者的跟踪控制,提出了一个与模型无关的控制器,运用图论、实用稳定性理论以及矩阵分析等工具,实现了多
跟随者对单动态领航者的实用跟踪,并基于Matlab软件,通过数值仿真实验,验证了理论结果的正确性。如何对跟踪误差值进行估计并优化或者实现完全跟踪等问题都将是下一步的研究方向。
[1] Mei J, Ren W, Chen J, et al. Distributed adaptive coordination for multiple Lagrangian systems under a directed graph without using neighbors’ velocity information[J]. Automatica, 2013, 49(6): 1723-1731.
[2] Dong W J. On consensus algorithms of multiple uncertain mechanical systems with a reference trajectory[J]. Automatica, 2011, 47(9): 2023-2028.
[3] Wang H L, Wu X F, Chen Y, et al. Distributed coordinated tracking for the Lagrange network systems via quantized data exchange[C]. Proceedings of 4thChinese Automation Conference, Wuhan, 2015: 1086-1091.
[4] 梅杰, 张海博, 马广富. 有向图中网络Euler-Lagrange系统的自适应协调跟踪[J]. 自动化学报, 2011, 37(5): 596-603.
[5] 王怀龙, 吴晓锋, 陈云, 等. 量化和噪声约束条件下多Lagrange航行体编队的分布式跟踪控制[J]. 海军工程大学学报, 2016, 28(5): 51-56.
[6] Abdessameud A, Polushin I G, Tayebi A. Synchronization of lagrangian systems with irregular communication delays[J]. IEEE Transactions on Automatic Control, 2014, 59(1): 187-193.
[7] Chen G, Lewis F L. Distributed adaptive tracking control for synchronization of unknown networked Lagrangian systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2011, 41(3): 805-816.
[8] Li L L, Ho D W C, Lu J Q. A unified approach to practical consensus with quantized data and time delay[J]. IEEE Transactions on Circuits and Systems, 2013, 60(10): 2668-2678.
[9] 王怀龙, 吴晓锋, 陈云, 等. 多拉格朗日航行体编队在量化及噪声下的集结[J]. 华中科技大学学报(自然科学版), 2016, 44(8): 46-51.
Dynamic Tracking Control for the Multi-agent Formation Via Time Delay
DAI Guo-zhong, WANG Huai-long
(The PLA Unit 91655, Beijing 100036, China)
For the dynamic tracking problem of the multi-agent formation with time delay, a model-independent control algorithm is proposed, and all followers can track a dynamic leader practically in a directed graph of time delay based on the practical stability theory, graph theory and matrix analysis. 3-DOF UUV as numerical simulations can prove the correctness of the algorithms based on the LMI toolbox of Matlab.
the multi-agent formation; dynamic tracking; model-independent; time delay; UUV
2017-02-15
戴国忠(1971-),男,江苏无锡人,高级工程师,研究方向为指挥自动化。 王怀龙(1988-),男,博士,工程师。
1673-3819(2017)03-0036-04
TP242.6;E917
A
10.3969/j.issn.1673-3819.2017.03.008
修回日期: 2017-03-12
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

