完全活性空间组态相互作用能量的拟合和外推
曹静思 陈飞武*
(北京科技大学化学与生物工程学院化学与化学工程系,功能分子与晶态材料科学与应用北京市重点实验室,北京 100083)
完全活性空间组态相互作用能量的拟合和外推
曹静思 陈飞武*
(北京科技大学化学与生物工程学院化学与化学工程系,功能分子与晶态材料科学与应用北京市重点实验室,北京 100083)
完全活性空间组态相互作用计算与完全活性空间中的活性电子数和活性轨道数有关,但完全活性空间组态相互作用的能量不是活性电子数和活性轨道数的单调递减函数,因此活性轨道数和活性电子数不能用来外推完全活性空间组态相互作用的能量。为此,我们定义了一个新的变量:活性空间中的最大未占满轨道数。我们对一系列单重态、双重态和三重态分子进行了完全活性空间组态相互作用的计算,并利用活性空间中的活性电子数和最大未占满轨道数这两个变量,对这些基态能量进行了拟合和外推,拟合的均方根误差都在10-6数量级。外推能量的精度优于MP4,对小分子体系,其精度高于CCSD。外推的完全的组态相互作用(FCI)能量值和实际计算的FCI值也很接近。另外,我们还利用外推能量来优化双原子分子的平衡键长,并计算谐振频率,其精度优于CASSCF。
活性空间;活性电子;活性轨道;能量外推;键长;谐振频率
1 引 言
应用量子化学方法可以计算分子体系能量1、优化几何结构2,3、分析反应活性4-7和分子内取代基效应8、讨论分子间的相互作用9-11以及反应速率12,13等。Hartree-Fock方法是重要的量子化学计算方法之一,它基于独立粒子近似,但没有考虑电子之间的相关能。为了获得高精度的计算结果,需要采用高级别的量子化学计算方法,如组态相互作用方法、微扰方法、耦合簇方法等。由于这些方法的计算量都比Hartree-Fock方法的计算量大很多,这些方法主要应用在小分子体系14-18。另外,在同一级别的计算中,如MP2,我们也可以采用大的基组来提高计算的精度。对于中小体系,通过这种办法,甚至可以得到基组极限时的计算结果。
体系的能量是基函数数目的单调递减函数,即随着基函数数目的增加,体系的能量逐渐降低,并趋向基组极限值。利用这一性质,常常将有限基组时的计算结果外推至基组极限。此方法最初是由Schwartz于1963年提出19,后经Kutzelnigg20和Feller21等进一步推广,基函数外推方法得到了广泛应用20-29。基函数外推法既可以对体系的总能量直接外推,也可以分别对Hartree-Fock能量和电子相关能进行外推,然后再求总能量。Hartree-Fock能量随着基函数的增大,收敛较快,外推公式呈指数形式。电子相关能对基函数收敛较慢,外推公式采用多项式的形式。目前外推公式形式很多,有兴趣的读者请参看文献22和26。
在给定的基组下,完全的组态相互作用(FCI)方法能够得到电子全部的相关能。FCI是目前最为精确的计算方法,其能量满足变分上限性质,具有大小一致性30。然而当体系的电子数较多时,FCI展开式中的组态函数数目非常大,FCI计算量更是巨大。因此,能否也像基函数外推一样,对FCI的能量进行外推呢?完全活性空间组态相互作用方法(CASCI)就是在活性空间中进行FCI计算。CASCI能量具有大小一致性。对一个给定的体系,CASCI计算涉及两个变量:完全活性空间的活性轨道数和活性电子数。因此,在CASCI计算中,CASCI能量与完全活性空间中的活性分子轨道数和活性电子数有关。但是,我们发现,体系的CASCI能量并不是活性轨道数和活性电子数的单调递减函数。当固定体系的活性电子数时,能量随活性轨道数的增加而逐渐降低,但当固定体系的活性轨道数时,能量最低点并不在活性电子数的最大处。由此可见,体系的活性轨道数和活性电子数不适合用来外推CASCI能量。我们需要寻找新的自变量来代替活性轨道数或活性电子数,CASCI能量将是它们的单调函数,从而方便能量的外推。
本文中,我们定义了一个新的自变量。CASCI能量是该自变量和活性电子数的单调递减函数。本文共选取了20个分子体系进行CASCI能量计算,其中单重态分子8个、双重态分子5个以及三重态分子7个。我们对CASCI能量进行了数值拟合。这些拟合的公式可以用来外推FCI的能量。另外,我们还利用外推的FCI能量来优化双原子分子的平衡键长,并计算谐振频率。
2 计算方法
众所周知,对一个分子体系,若分子的活性轨道数为M,活性电子数为N,考虑自旋对称性限制(不考虑空间对称性限制),其总自旋为S的组态函数的数目n为31:
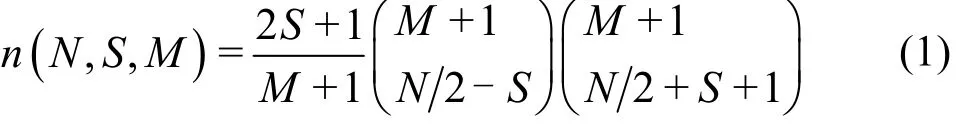
n随着M和N的增加而快速的增长。在CASCI计算中,在总自旋S不变的前提下,组态的个数n是由活性空间中的轨道数和电子数决定的。一般来说,活性轨道数和活性电子数越大,计算的能量越精确。但当固定体系的活性轨道时,体系的活性电子数与CASCI能量之间的关系不是单调递减的关系。因此,分子的活性轨道数和活性电子数不适合作为外推CASCI能量的自变量。为此,我们定义了一个新的自变量Mmax:
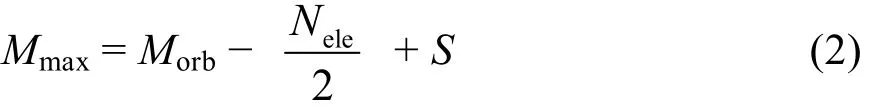
其中Nele为完全活性空间中的活性电子数,Morb为活性轨道数。从式(2)看出,Mmax实际上就是活性空间内最大未占满轨道数。在计算中我们发现,若固定活性空间中的电子数Nele,则活性空间中最大未占满轨道数Mmax越大,体系的能量越低;同样,若活性空间中最大未占满轨道数Mmax不变,则活性空间中的电子数Nele越大,体系的能量也越低。由此可见,CASCI能量是Nele和Mmax的单调递减函数,可以用来进行能量外推。为了方便能量的拟合,对于体系的能量做如下处理:

ECASCI表示CASCI计算得到的能量,N为体系的总电子数,a = 1 a.u.。和ECASCI不一样,如果仍将E看成Mmax和Nele的函数,则E是这两个变量的单调递增函数,即活性空间中的电子数或最大未占满轨道数越大,E越大。通过对不同类型公式的拟合试算,我们发现如下公式比较适合CASCI能量的拟合以及能量的外推:
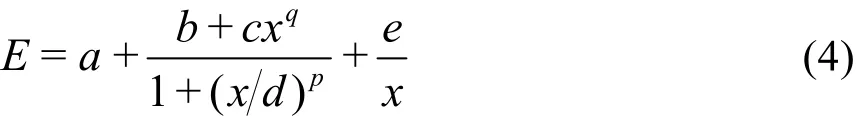
公式中,a、b、c、d、e、p和q为待定的拟合系数,x为活性电子数Nele或最大未占满轨道数Mmax。当活性空间中的电子数Nele固定时,式(4)用于拟合E和Mmax之间的函数关系;同样,当为活性空间中最大未占满轨道数Mmax固定时,式(4)用于拟合E与Nele的函数关系。由于式(4)中的xq和1/x项都是对E的微小校正,若已计算出来的CASCI能量数据量不足,则将它们忽略,采用如下简化的公式进行能量拟合:
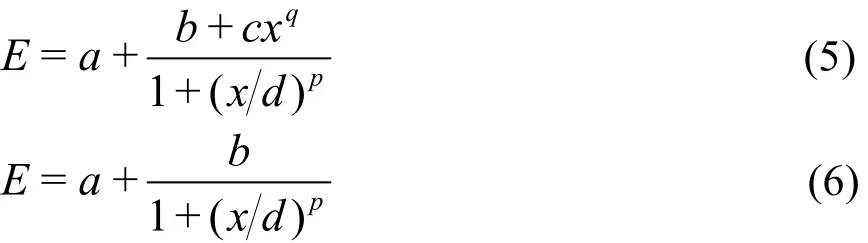
下面以式(4)为例来说明当活性电子数固定时如何进行能量的拟合和外推。对于一个给定的体系,当Nele固定为某一数值时,通过拟合一系列的E和Mmax数值,可以确定式(4)中的待定系数a、b、c、d、e、p和q。在这一系列的Mmax值中,由于计算量太大,可能不包含最大的Mmax。将这个最大的Mmax代入式(4)中算出E,进而利用式(3)换算成ECASCI。ECASCI就是活性电子数固定为Nele时外推得到的CASCI能量。如果Nele等于体系的总电子数,则ECASCI为外推得到的FCI能量。如果采用冻核近似(frozen core),Nele等于总电子数减去冻结的电子数,则外推的能量为冻核近似时的FCI能量。当Mmax固定时,对E和Nele数值的拟合和外推是类似的,不再赘述。
本文采用Gaussian 03程序32,分别用RHF和ROHF方法对单重态分子和多重态分子进行几何构型优化。几何结构优化的基组为6-31G(d,p)33,其他计算时采用稍小的基组6-31G。CASCI能量用Gamess 09程序计算34,35,单重态分子和多重态分子分别采用HF和ROHF轨道。
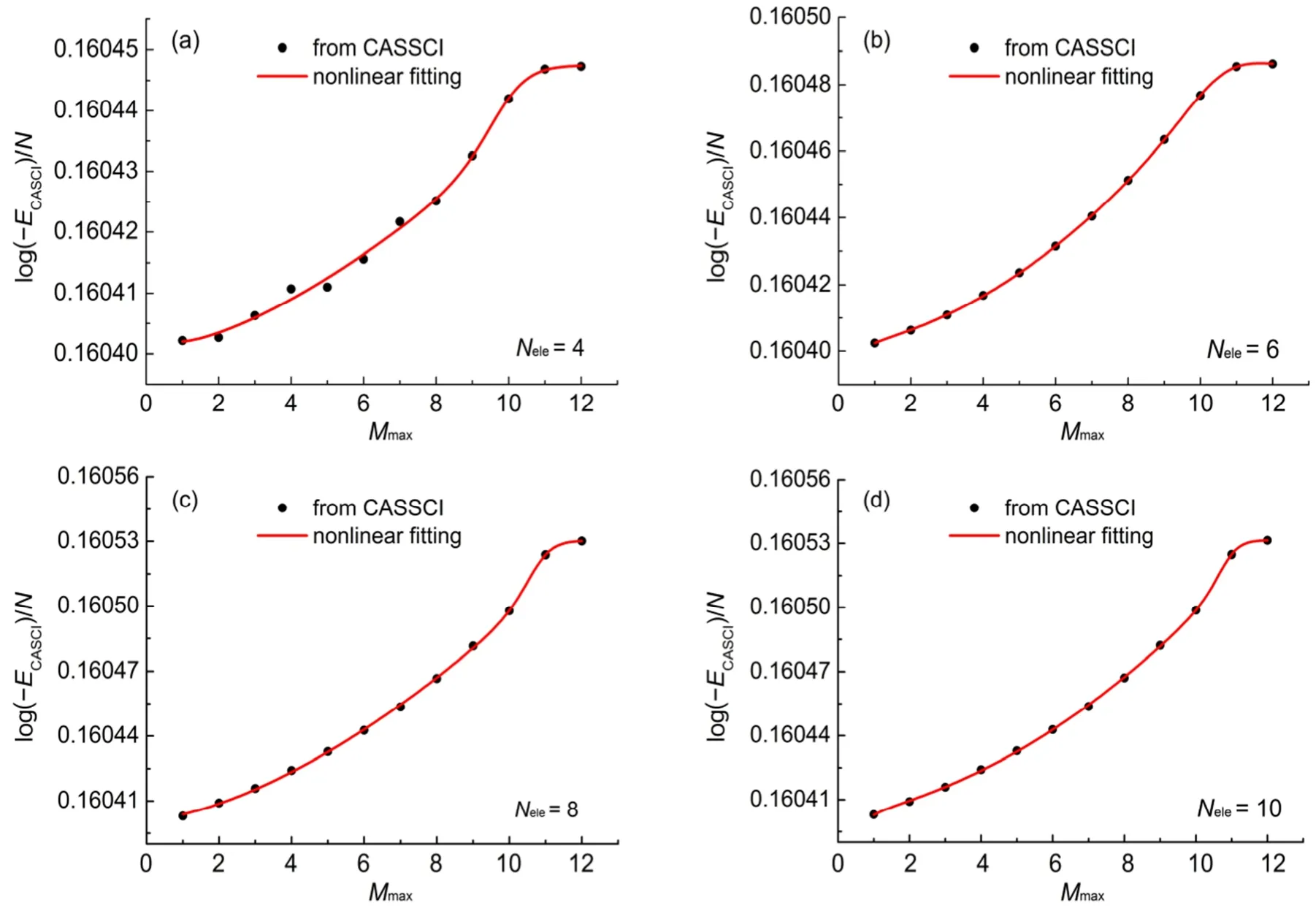
图1 CH4分子的E与活性空间中最大未占满轨道数Mmax的关系图Fig.1 Diagram of E vs the maximum number of unoccupied orbitals Mmaxof CH4
3 结果与讨论
本文主要分为三个部分进行讨论:单重态分子体系CASCI能量拟合与FCI能量外推计算、多重态分子体系CASCI能量拟合与FCI能量外推计算、双原子分子平衡键长与谐振频率的计算。
3.1 单重态分子体系CASCI能量拟合与外推
我们利用公式(4)、(5)、(6)对CH4、H2O、HF、C2H4、N2H4、HCl、Cl2和O3共8个单重态分子进行了CASCI能量的计算和拟合。我们选择CH4作为例子,从图形的角度来显示对CASCI能量的拟合效果。图1给出了E与最大未占满轨道数Mmax的曲线,其中图(a)、(b)、(c)和(d)分别为活性空间中的电子数Nele为4、6、8和10时,E与最大未占满轨道数Mmax的曲线。图中黑色实心圆点为计算得到的E值,红线为拟合曲线,右下角为活性空间中固定的电子数。拟合公式为式(4)。从图1中可以看出,随着活性空间中电子数不断增加,CASCI能量越来越低,E越来越大,并且趋近于一个稳定的值。随着活性电子数Nele的增加,E与最大未占满轨道数拟合的均方根误差也在逐渐减小,拟合的精度越来越高。图1中E-Mmax拟合曲线的回归系数都在0.99以上,均方根误差均在10-6量级,其中最大者为1.2608 × 10-6,最小者为0.1703 × 10-6。随着固定的活性电子数逐渐增大,拟合公式中的拟合参数逐渐减小,如在活性电子数为2、4、6、8、10时,参数a的值为-49.737444、-49.752398、-49.770648、-49.794475和-49.940153,参数b的值为-49.607330、-49.728629、-49.730728、-49.732492和-49.733193。
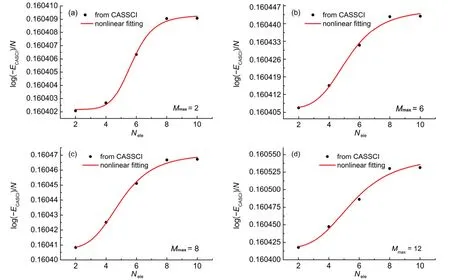
图2 CH4分子E与活性电子数Nele的关系图Fig.2 Diagram of E vs the number of active electron Neleof CH4
图2 同样以CH4分子为例,给出了在活性空间中取不同的最大未占满轨道数Mmax时,E与活性电子数Nele的曲线。图(a)、(b)、(c)和(d)分别对应活性空间中最大未占满轨道数Mmax为2、6、8、12时的曲线。由于CH4分子较小,总电子数为10,计算出来的数据量不多,因此采用公式(6)进行拟合。拟合的回归系数都在0.98以上,均方根误差均在10-6量级。从图2中看出,随着活性电子数的增加,E越来越大,且趋于收敛。除CH4外,对H2O、HF、C2H4、N2H4、HCl、Cl2和O3的拟合结果是类似的,不再赘述。
表1给出了CH4、H2O、HF、C2H4、N2H4、HCl、Cl2和O3分子在活性空间中的电子数Nele固定时的拟合和外推结果。表1中第2至6列列出了CASCI的外推能量。从表1中可以看出,随着活性电子数的增加,外推能量也逐渐降低。CH4、H2O和HF分子的总电子数均为10,因此,当活性电子数Nele等于10时,则可以外推出FCI能量。表1中对CH4、H2O和HF分子外推得到的FCI能量分别为-40.300837、-76.119450和-100.114677 hartree。在6-31G基组时,对CH4、H2O和HF分子实际计算得到的FCI能量值分别为-40.300835、-76.120838和-100.114307 hartree。比较这两组数据,可以看出外推得到的FCI能量和实际计算的FCI能量很接近。表1中第7、8列为对E-Mmax拟合的回归系数的平均值(R2-M)和均方根误差的平均值(Se-M)。本文中8个单重态分子的拟合回归系数的平均值R2-M都在0.97以上,均方根误差的平均值Se-M均小于10-5,其中最大者为1.82179 × 10-6,最小者为0.01351 × 10-6,这说明拟合的效果非常不错。
表2中列出了6种不同计算方法对上述8个分子在平衡结构时计算得到的单点能。这6种方法分别为B3LYP、MP2、MP4、CCSD、外推法(简记为Extra.)和FCI,它们的计算结果分别列在表2的第2至7列。由于计算量太大,第7列只给出了CH4、H2O和HF分子的FCI计算结果。从表2可知,对HF、HCl和O3分子,采用B3LYP计算得到的能量明显偏低。除H2O外,对表中的其他分子,CCSD的计算精度都比MP4高。对CH4、H2O、HF、C2H4和N2H4,外推能量比CCSD更低,更接近体系的精确能量值。但是,对HCl、Cl2和O3分子,由于体系的电子数增多,计算量增大,计算时的固定电子数Nele还不够大,因此外推能量的精度可能比CCSD稍低。表1中HCl的外推能量比表2中HCl的外推能量稍高,是因为后者的活性电子数为14的缘故。
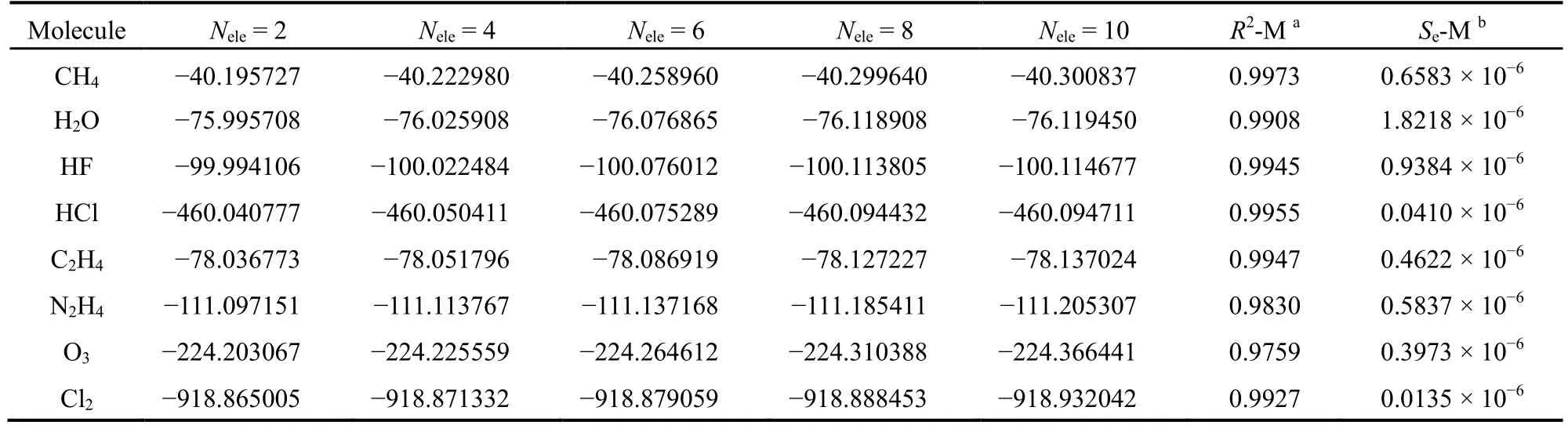
表1 单重态分子的外推能量(hartree)及拟合参数Table 1 Extrapolated energies (hartree) of singlet molecules and fitting parameters
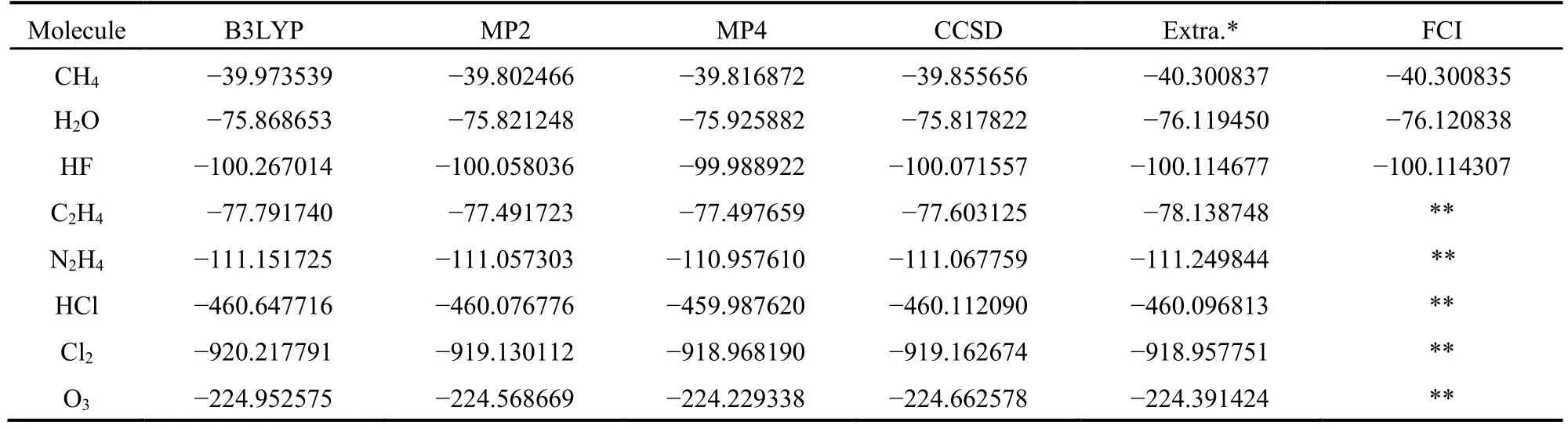
表2 利用6种方法计算单重态分子的单点能(hartree)Table 2 Energies (hartree) of singlet molecules calculated with six methods
3.2 多重态分子体系CASCI能量拟合与能量外推计算
对于多重态分子体系,我们选取了CH、NH2、MgH、CN和NO共5个双重态分子,以及CH2、NH、OH+、PH、NF、SiH2和O2共7个三重态分子,用于CASCI能量的拟合和外推。我们以双重态分子MgH为例,在图3中给出了在活性空间中取不同电子数Nele时,E与最大未占满轨道数Mmax的关系图,红线为拟合曲线,每个小图的右下角给出了该图中固定的活性电子数(Nele)。图中E-Mmax曲线都是利用式(5)拟合的,其拟合曲线的回归系数都在0.98以上,拟合均方根误差都在10-6数量级。从图3可看出,活性空间中的电子数越多,其E-Mmax曲线越平滑,拟合曲线得到的拟合均方根误差也随之减小。当Nele= 11时,拟合曲线的回归系数为0.99,均方根误差低至0.14 × 10-6。随着固定的活性电子数逐渐增大,拟合公式中的拟合参数逐渐减小,如在活性电子数为3、5、7、9、11时,参数a的值为-99.878316、-99.878368、-99.878564、-99.879120和-99.879244,参数b的值为-99.872269、-99.872276、-99.872407、-99.872513和-99.872558。比较图3(c)和(d),可以发现,当活性空间中的电子达到11时,增加电子数并不能使分子的E-Mmax曲线变得更平滑,这是因为MgH分子含有的13个电子中,内层1s轨道中的电子对分子的能量影响很小,这也是在通常的CASCI计算中,都会冻结1s轨道的电子以减少计算所需的时间和内存的原因。
图4以三重态O2分子为例,给出了在活性空间中取不同的电子数Nele时,E与最大未占满轨道数Mmax的关系图。从图4(a)中可以看到,当活性空间中的电子为6时,增加轨道数,得到的E-Mmax曲线呈现阶梯状,拟合效果较差。随着电子数的增加,能量曲线越来越平滑,拟合曲线的均方根误差均有较大改善。这也说明进行CASCI能量计算时,选择适当的活性空间电子数的重要性。与闭壳层体系的讨论类似,开壳层分子体系也可以固定最大未占满轨道数Mmax,对E和活性空间电子数Nele之间的函数关系进行拟合,我们采用式(4)、(5)和(6)拟合的回归系数均大于0.95和均方根误差小于10-6,为避免雷同,没有另外给出它们的图形。
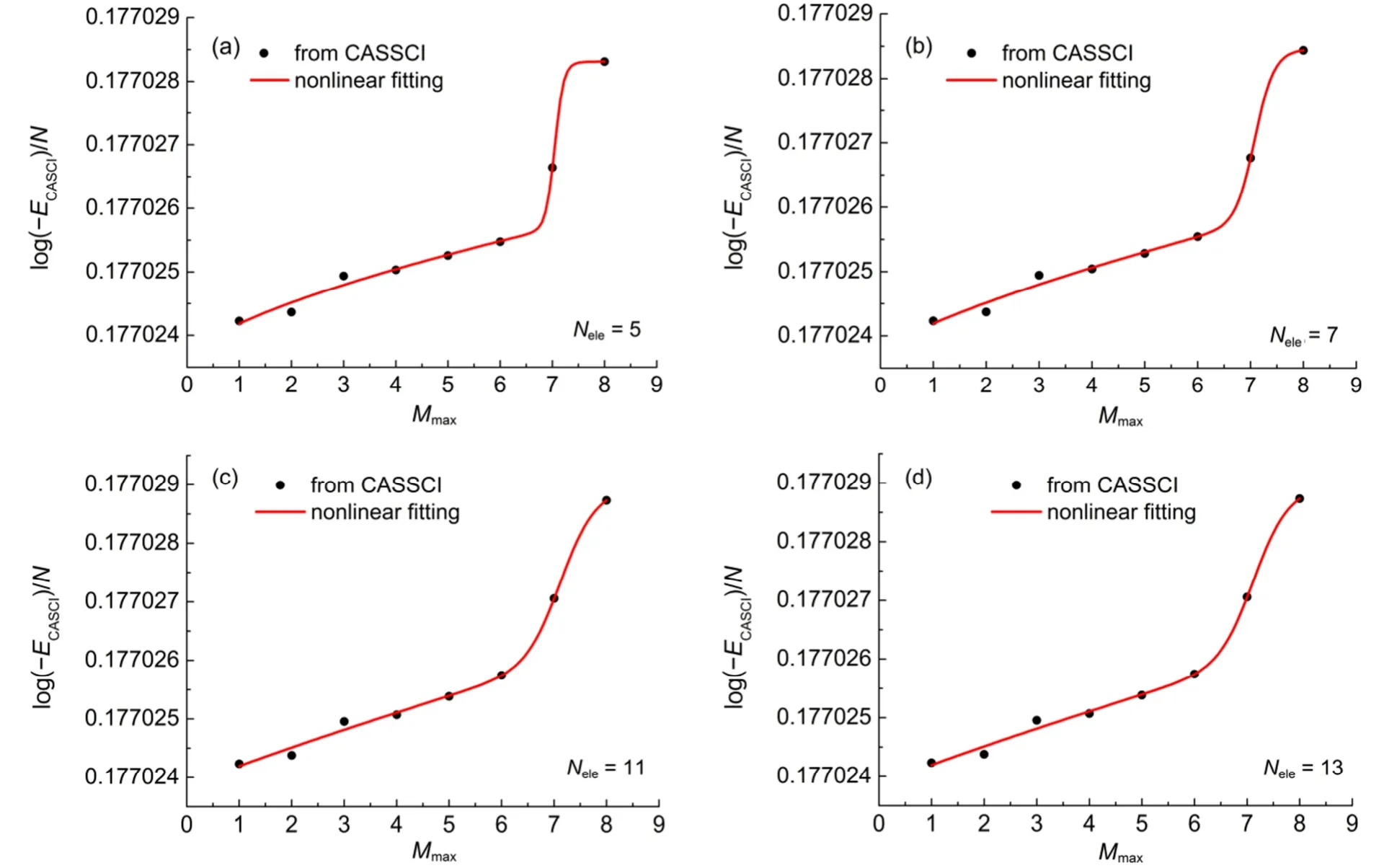
图3 MgH分子E与活性空间中最大未占满轨道数Mmax的关系图Fig.3 Diagram of E vs the maximum number of unoccupied orbitals Mmaxof MgH
当活性空间中的电子数固定时,对双重态分子CH、NH2、MgH、CN和NO以及三重态分子CH2、NH、OH+、PH、NF、SiH2和O2的E与最大未占满轨道数Mmax进行拟合和外推,结果列在表3中。和表1中对单重态分子的讨论类似,随着固定电子数Nele增加,双重态和三重态分子的外推能量都逐渐降低,并向体系的FCI能量值方向收敛。表中第7和8列分别列出了拟合曲线回归系数的平均值和均方根误差的平均值。从表中看出,所有双重态和三重态分子的拟合平均回归系数都达到0.98甚至0.98以上,平均均方根误差也在10-6数量级,这说明拟合效果不错。但对双重态分子CN和NO,当活性轨道中的电子数为3时,利用式(5)拟合的效果不好,回归系数在0.95以下,因此表中第2列没有列出它们的外推能量值。对三重态分子SiH2和O2,当活性电子数为2时,也出现同样的情形。发生这两种情形的原因是活性电子数较小时点(Mmax,E)的分布不规则,甚至出现阶梯型造成的。因此,进行曲线的拟合和能量外推时,在计算资源允许的情况下,体系的活性电子数Nele应尽量选得大一些。
和表2的讨论类似,我们采用6种不同的方法,计算了5个双重态分子和7个三重态分子在平衡几何结构时的单点能,具体结果列在表4中。这6种方法分别为B3LYP、MP2、MP4、CCSD、外推法(简记为Extra.)和FCI。从表4中看出,除了双重态NH2和三重态CH2外,对其它分子,UB3LYP算出的基态能量都明显偏低。和UMP4的计算结果相比,UMP2对所有分子计算的基态能量都明显偏低。除PH分子外,UCCSD和外推能量的精度均比UMP4的精度高。对PH、NF和SiH2三个分子,它们的外推能量比UCCSD计算的能量稍高,其他分子的外推能量都比UCCSD计算的能量低。从表4还可看出,对双重态分子CH、NH2和MgH以及三重态分子CH2、NH和OH+,外推的FCI能量值和实际的FCI能量计算值非常接近,差值至少在10-3hartree数量级。综合表2和表4的结果,可以看出无论是对单重态分子、双重态分子还是对三重态分子,外推能量值是可靠的,其精度是有保证的。
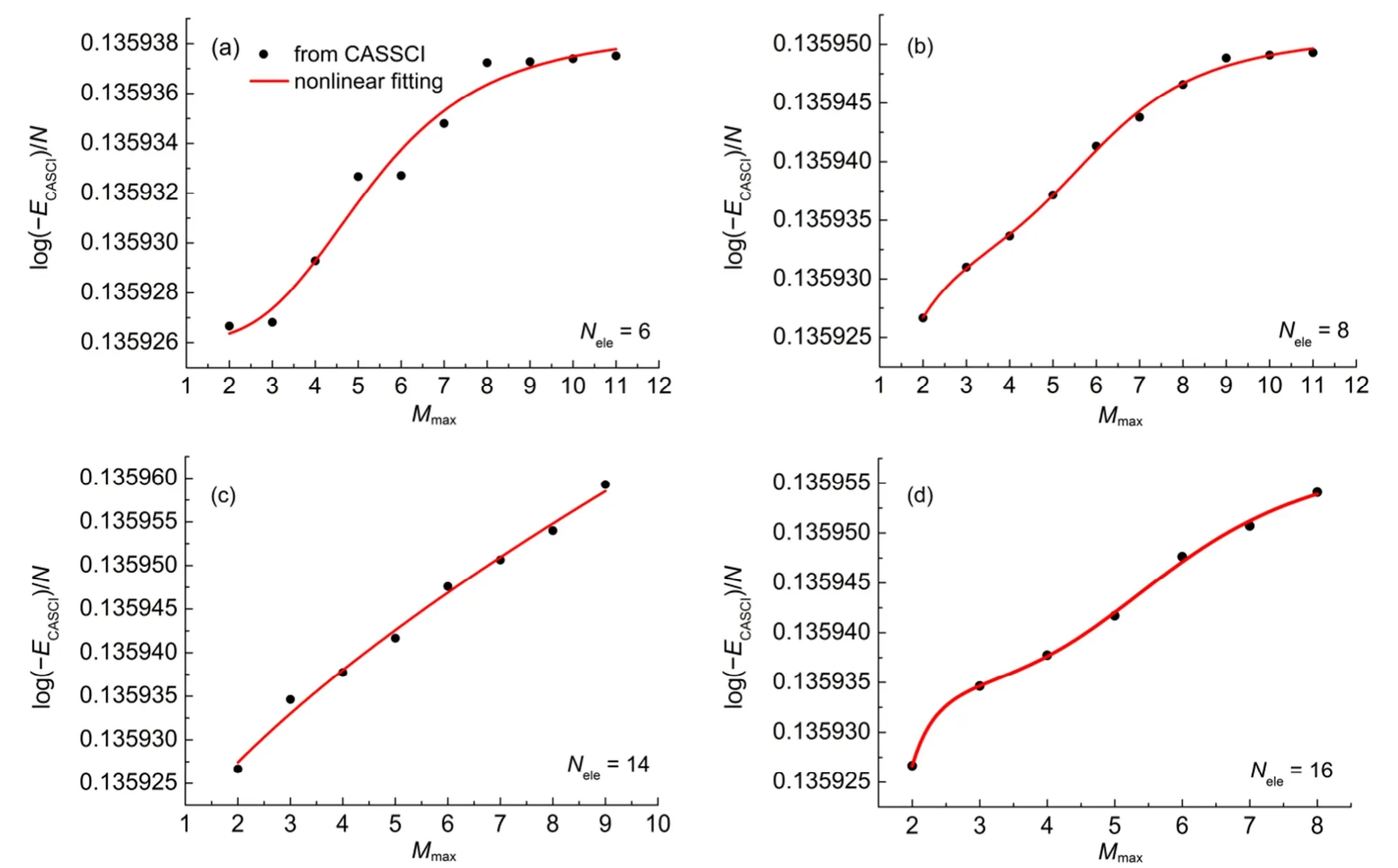
图4 O2分子E与活性空间中最大未占满轨道数Mmax的关系图Fig.4 Diagram of E vs the maximum number of unoccupied orbitals Mmaxof O2

表3 多重态分子的外推能量(hartree)及拟合参数Table 3 Extrapolated energies (hartree) of multiplet molecules and fitting parameters
3.3 双原子分子平衡键长与谐振频率的计算
我们采用HF、MP2、CASSCF和外推能量优化了单重态、双重态和三重态共6个双原子分子的键长,并计算了谐振频率,结果列于表536中。HF和MP2的结果是采用Gaussian 0332计算的,CASSCF的结果是采用Gamess 0934计算得到的,外推能量是采用我们课题组的程序计算的。利用外推能量优化键长时,我们在平衡点附近等间距地选取7个点,间距为0.01 × 10-10m。然后对这7个点的外推能量值采用Murrell-Sorbie函数或多项式进行拟合,最后计算出了平衡键长和谐振频率37-39。从表5中可以看到,对单重态分子,HF和MP2的计算精度稍优,对双重态和三重态分子,CASSCF和外推能量的效果更好。和CASSCF计算结果相比较,外推能量得到的键长和谐振频率更接近实验值。由于外推能量受拟合精度的影响,能得到这样的结果还是令人满意的。

表4 利用6种方法计算多重态分子的单点能(hartree)Table 4 Energies (hartree) of multiplet molecules calculated with six methods
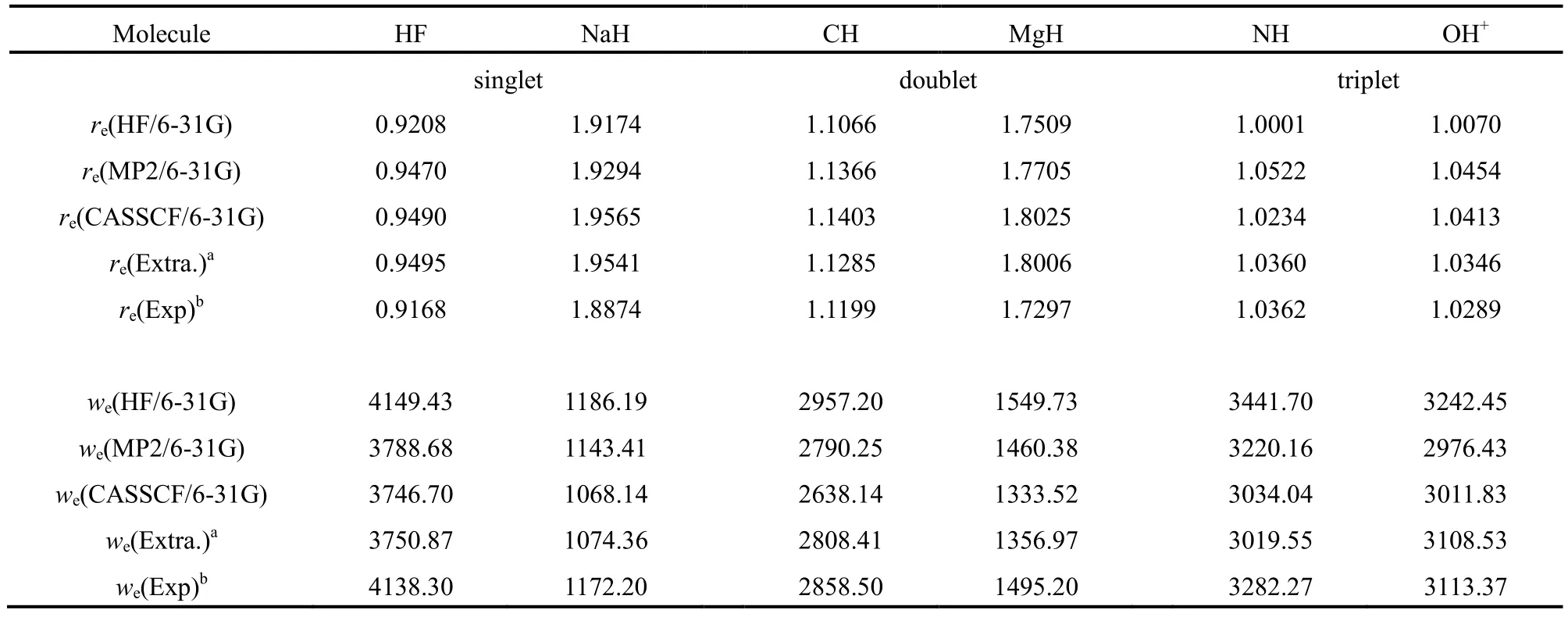
表5 4种方法计算的平衡键长(re, 10-10m)和谐振频率(we, cm-1)的比较Table 5 Comparison of the bond length (re, 10-10m) and harmonic frequency (we, cm-1) calculated with four methods
4 结 论
CASCI能量与活性空间中的分子轨道数和电子数有关,但CASCI能量并不是活性轨道数和活性电子数的单调函数,因此,活性轨道数和活性电子数不能作为CASCI能量外推的自变量。为此,我们定义了一个新的变量:活性空间中最大未占满轨道数。用活性电子数和最大未占满轨道数作为拟合CASCI能量的两个变量,我们找到了比较合适的CASCI能量拟合公式。利用该公式,可以进行能量外推,甚至外推出FCI的能量。我们对一系列单重态分子、双重态分子和三重态分子进行了CASCI能量的拟合,拟合精度都在10-6数量级。从这些算例,我们看出外推能量的精度比MP2和MP4的精度都高。如果活性电子数足够大,外推能量的精度比CCSD还高。外推的FCI能量值和实际计算出来的FCI能量值很接近,最大的差值也在10-3hartree数量级。这些结果均说明对CASCI能量的拟合和外推是可靠的,外推能量的精度是有保证的。
另外,我们还利用能量外推法对6个单重态、双重态和三重态分子的平衡键长进行了优化,并算出平衡构型时的谐振频率。对三重态分子NH,能量外推法得到的精度和CASSCF的精度基本相当,但对其他5个分子,能量外推法的结果明显比CASSCF方法的结果更接近实验值。能量外推法的精度依赖于CASCI能量的拟合精度。进行键长优化时它还要求平衡点附近势能曲线的精度要非常一致,否则,势能曲线的形状对平衡键长和谐振频率的影响较大。由此可见,利用能量外推法进行分子几何结构优化是不容易的。提高能量外推法在结构优化时的精度值得我们深入研究。
(1) Jensen, F. Introduction to Computational Chemistry, 2nd ed.; West Sussex: John Wiley & Sons, 2007; p 487.
(2) Cao, J. S.; Wei, M. J.; Chen, F. W. Acta Phys. -Chim. Sin. 2016, 32 (7), 1639. [曹静思, 韦美菊, 陈飞武. 物理化学学报, 2016, 32 (7), 1639.] doi: 10.3866/PKU.WHXB201604062
(3) Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, New York, 1960.
(4) Fu, R.; Lu, T.; Chen, F. W. Acta Phys. -Chim. Sin. 2014, 30 (4), 628. [付 蓉, 卢 天, 陈飞武. 物理化学学报, 2014, 30 (4), 628.] doi: 10.3866/PKU.WHXB201401211
(5) Zhou, X. Y.; Rong, C. Y.; Lu, T.; Liu, S. B. Acta Phys. -Chim. Sin. 2014, 30 (11), 2055. [周夏禹, 荣春英, 卢 天, 刘述斌.物理化学学报, 2014, 30 (11), 2055.] doi: 10.3866/PKU.WHXB201409193
(6) Cao, J. S.; Ren, Q.; Chen, F. W.; Lu, T. Sci. China Chem. 2015, 58 (12), 1845. doi: 10.1007/s11426-015-5494-7
(7) Liu, S. B. Acta Phys. -Chim. Sin. 2016, 32 (1), 98. [刘述斌. 物理化学学报, 2016, 32 (1), 98.] doi: 10.3866/PKU.WHXB201510302
(8) Luo, Q. Q.; Cao, C. T.; Cao, C. Z. Acta Phys. -Chim. Sin. 2016, 32 (7), 1691. [罗青青, 曹朝暾, 曹晨忠. 物理化学学报, 2016, 32 (7), 1691.] doi: 10.3866/PKU.WHXB201604061
(9) Lu, T.; Chen, F. W. J. Mol. Model. 2013, 19 (12), 5387. doi: 10.1007/s00894-013-2034-2
(10) Esrafili, M. D.; Mohammadian-Sabet, F. Int. J. Quantum Chem. 2016, 116 (7), 529. doi: 10.1002/qua.25076
(11) Zhao, Q.; Qi, B. Y.; Wang, B. J.; Chen, F. W. Acta Chim. Sin. 2015, 74 (3), 285. [赵 清, 齐博宇, 王宝金, 陈飞武. 化学学报, 2015, 74 (3), 285.] doi: 10.6023/A15100641
(12) Horn, M.; Schappele, L. H.; Lang-Wittkowski, G.; Mayr, H.; Ofial, A. R. Chem. -Eur. J. 2013, 19 (1), 249. doi: 10.1002/chem.201202839
(13) Cao, J. S.; Chen, F. W. Chin. J. Org. Chem. 2016, 36 (10), 2463. [曹静思, 陈飞武. 有机化学, 2016, 36 (10), 2463.] doi: 10.6023/cjoc201602026
(14) Bartlett, R. J.; Purvis, G. D. Int. J. Quantum Chem. 1978, 14 (5), 561. doi: 10.1002/qua.560140504
(15) Chen, F. W. J. Chem. Theory Comput. 2009, 5 (4), 931. doi: 10.1021/ct800546g
(16) Fan, Z. H.; Chen, F. W. Acta Phys. -Chim. Sin. 2015, 31 (11), 2064. [范志辉, 陈飞武. 物理化学学报, 2015, 31 (11), 2064.] doi: 10.3866/PKU.WHXB201508201
(17) Li, W.; Ni, Z.; Li, S. Mol. Phys. 2016, 114 (9), 1447. doi: 10.1080/00268976.2016.1139755
(18) Liu, W. J.; Hoffmann M. R. J. Chem. Theory Comput. 2016, 12 (3), 1169. doi: 10.1021/acs.jctc.5b01099
(19) Schwartz, C. Phys. Rev. 1962, 126 (3), 1015. doi: 10.1103/PhysRev.126.1015
(20) Kutzelnigg, W.; Morgan, J. D., III J. Chem. Phys. 1992, 96 (6), 4484. doi: 10.1063/1.462811
(21) Feller, D. J. Chem. Phys. 1993, 98 (9), 7059. doi: 10.1063/1.464749
(22) Feller, D.; Peterson, K. A.; Hill, J. G. J. Chem. Phys. 2011, 135 (4), 044102. doi: 10.1063/1.3613639
(23) Peterson, K. A.; Woon, D. E.; Dunning, T. H., Jr. J. Chem. Phys. 1994, 100 (10), 7410. doi: 10.1063/1.466884
(24) Feller, D. J. Chem. Phys. 2013, 138 (7), 074103. doi: 10.1063/1.4791560
(25) Martin, J. M. L. Chem. Phys. Lett. 1996, 259 (5), 669.doi: 10.1016/0009-2614(96)00898-6
(26) Seino, J.; Nakai, H. J. Comput. Chem. 2016, 37 (25), 2304. doi: 10.1002/jcc.2455
(27) Tu, Z. Y.; Wang, W. L. Acta Phys. -Chim. Sin. 2015, 31 (6), 1054. [涂喆研, 王文亮. 物理化学学报, 2015, 31 (6), 1054.] doi: 10.3866/PKU.WHXB201503261
(28) Lin, X. F.; Sun, C. K.; Yang, S. Y.; Yu, S. W.; Yao, L. F.; Chen, Y. S. Acta Chim. Sin. 2011, 69 (23), 2787. [林雪飞, 孙成科, 杨思娅, 余仕问, 姚立峰, 陈益山. 化学学报, 2011, 69 (23), 2787.] doi: 10.6023/A1106172
(29) Li, S.; Chen, S. J.; Zhu, D. S.; Wei, J. J. Acta Phys. -Chim. Sin. 2013, 29 (4), 737. [李 松, 陈善俊, 朱德生, 韦建军. 物理化学学报, 2013, 29 (4), 737.] doi: 10.3866/PKU.WHXB201301311
(30) Daudey, J. P.; Heully, J. L.; Malrieu, J. P. J. Chem. Phys. 1993, 99 (2), 1240. doi: 10.1063/1.465368
(31) Veryazov, V.; Malmqvist, P. Å.; Roos B. O. Int. J. Quantum Chem. 2011, 111 (13), 3329. doi: 10.1002/qua.23068
(32) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; et al. Gaussian 03, Revision A.01; Gaussian Inc.: Pittsburgh, PA, 2003.
(33) Koseki, S.; Schmidt, M. W.; Gordon, M. S. J. Phys. Chem. 1992, 96 (26), 10768. doi: 10.1021/j100205a033
(34) Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen, J. J.; Koseki, S.; Matsunaga, N.; Nguyen, K. A.; Su, S.; Windus, T. L.; Dupuis, M.; Montgomery. J. A. J. Comput. Chem. 1993, 14 (11), 1347. doi: 10.1002/jcc.540141112
(35) Dykstra, C.; Frenking, G.; Kim, K.; Scuseria, G. Theory and Applications of Computational Chemistry: the First Forty Years; Amsterdam: Elsevier, 2005; p 1167.
(36) Huber, K. P. Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules; Springer: New York, 2013; p 8. doi: 10. 1007/978-1-4757-0961-2
(37) Chen, F. W.; Wei, M. J., Liu, W. J. Sci. China Chem. 2011, 54 (3), 446. doi: 10.1007/s11426-010-4199-1
(38) Chen, F. W.; Fan, Z. H. J. Comput. Chem. 2014, 35 (2), 121. doi: 10.1002/jcc.23471
(39) Wang, Z.; Wang, F. Phys. Chem. Chem. Phys. 2013, 15 (41), 17922. doi: 10.1039/c3cp51749g
Fitting and Extrapolation of Configuration Interaction Energies in Complete Active Space
CAO Jing-Si CHEN Fei-Wu*
(Department of Chemistry and Chemical Engineering, School of Chemistry and Biological Engineering, University of Science and Technology Beijing; Beijing Key Laboratory for Science and Application of Functional Molecular and Crystalline Materials, Beijing 100083, P. R. China)
Configuration interaction calculation in complete active space is related to the numbers of active electrons and orbitals. However, configuration interaction energy is not a monotonically decreasing function of these two variables. Thus, the numbers of active electrons and orbitals are not proper variables to extrapolate the configuration interaction energy. In order to address this problem, we defined a new variable: maximum number of unoccupied orbitals in the complete active space. We performed a series of configuration interaction calculations on singlet, doublet, and triplet molecules, and simulated their ground state energies with the number of active electrons and the number of maximum unoccupied orbitals. The mean square root errors of these simulations were on the order of 10-6. The accuracy of the extrapolated energies was better than that of MP4 and than that of CCSD for small molecules. The extrapolated full configuration interaction energies were very close to the energy values of full configuration interactions. Furthermore, the extrapolated energies were exploited to optimize the bond distances of several diatomic molecules and to compute harmonic vibrational frequencies. Their accuracies were better than that of the complete active space self-consistent field.
Complete active space; Active electron; Active orbital; Energy extrapolation; Bond length; Harmonic vibrational frequency
December 2, 2016; Revised: February 27, 2017; Published online: March 22, 2017.
O641
10.3866/PKU.WHXB201703221
*Corresponding author. Email: chenfeiwu@ustb.edu.cn; Tel: +86-10-62332689.
The project was supported by the National Natural Science Foundation of China (21173020, 21473008).
国家自然科学基金(21173020, 21473008)资助项目
© Editorial office of Acta Physico-Chimica Sinica

