化隐圆为显圆，破解动点问题

王少华

（湖北省武汉市梨园中学）

化隐圆为显圆，破解动点问题

王少华

（湖北省武汉市梨园中学）

文章首先介绍了几何问题中隐圆存在性的基本结论，再利用此结论来解决动点问题中的三类问题，分别是求解定值、求解最值和求解动点的运动路径长，最后总结了平时教学中的相关教学启示；化“隐”圆为“显”圆，可以很好地解决一类动点问题，分析、探索出一类通用的方法，为解决动点问题带来实际指导.

动点问题；定值问题；最值问题；运动路径

数学因运动而充满活力，数学因变化而精彩纷呈.动点问题是近几年的一个热点问题，以动点几何问题为基本框架而精心设计的试题，可谓璀璨夺目、精彩四射.有些动点问题，将圆隐藏在已知条件里，解题时，需要我们通过分析探索，发现这些隐藏的圆（以下统称“隐圆”），构造辅助圆，再利用相关的几何知识求解动点问题.

一、动点问题中隐圆存在性的基本结论

1.三角形隐藏的外接圆

（1）直角三角形隐藏的外接圆.

如图1，在Rt△ABC中，圆心即是斜边AB的中点，半径是OC.

（2）定角对定长的三角形隐藏的外接圆.

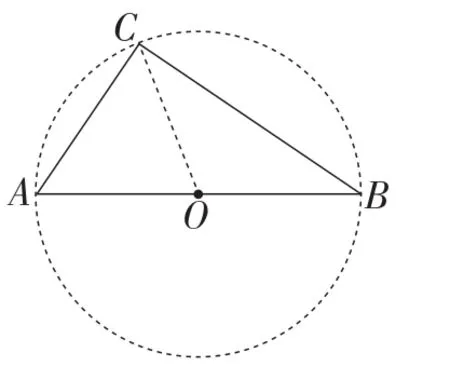
图1

在一个三角形中，定长的边长对应定值的内角，则存在一个隐圆，圆的半径是定值.由正弦定理可知，利用=2R可以求出圆的半径；初中几何中的一些特殊角，如45°或135°，60°或120°，30°或150°，可以用三角形和圆中的基础知识，结合勾股定理，得出圆的半径长.可以这样说，找准角和线，隐圆出来见.

如图2，已知线段AB=2，点C是直线AB上方一动点，∠C=30°，动点C在运动时构成什么样的图形？

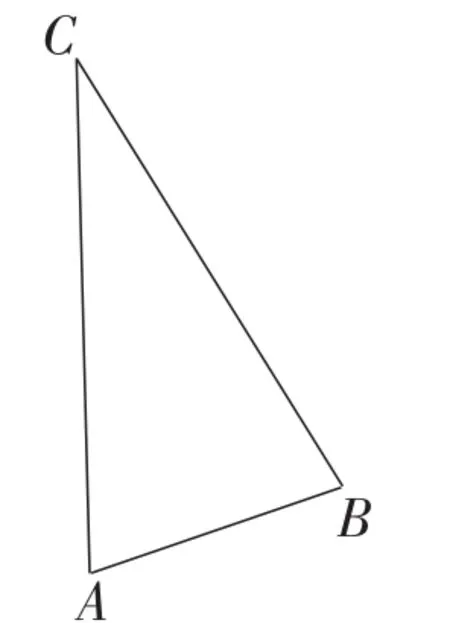
图2

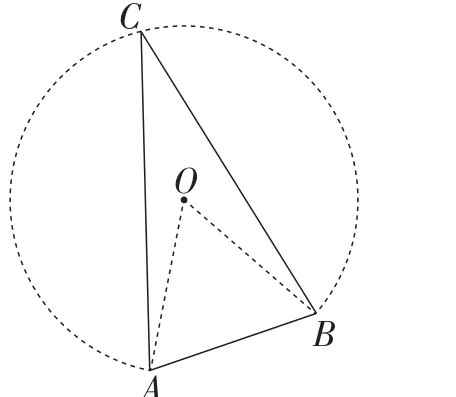
这个问题可以这样理解：A，B，C三点构成一个△ABC，点C是动点，△ABC是一个动三角形，但AB和∠C分别是一条定长的线段和一个定值的角，且线段AB所对的角是∠C.由圆中相等的圆周角所对的弦相等得到，点C在△ABC的外接圆上运动.如图3，画出△ABC的外接圆⊙O，则∠AOB=2∠C=60°，所以动点C构成⊙O的一段优弧.易证△AOB是等边三角形，圆的半径R=AB=2.直角三角形隐藏的外接圆可以看做是一种特殊情况.

2.特殊四边形隐藏的外接圆

（1）对角互补型四边形四点共圆.

如图4（1），∠ACB+∠ADB=180°；如图4（2），∠ACB=∠ADB=90°；如图4（3），∠ACB=∠BDE，则点A，B，C，D在同一个圆上.

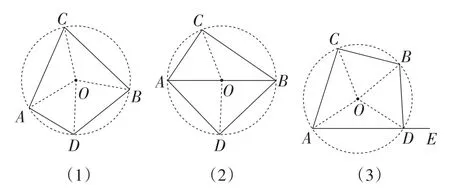
图4

（2）如果两个三角形有一条公共边，这条边所对的角相等，并且在公共边的同侧，那么这两个三角形有公共的外接圆.

如图5（1），边BC是公共边，∠BAC=∠BDC.如图5（2），边AB是公共边，则点A，B，C，D在同一个圆上，半径是OA.图5（2）是一种特殊情况.

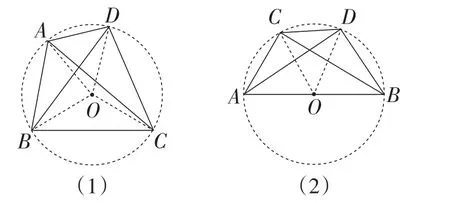
图5

（3）如果四边形的四个顶点到同一个点的距离相等，那么这个四边形有外接圆，如图6所示.

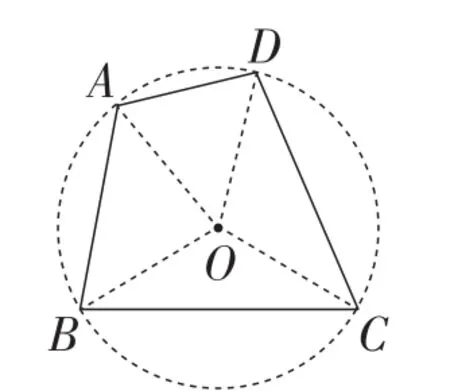
图6

上面的图形均来自于人教版教材九年级下册，是隐圆存在性的实际诠释.教材上的基本图形是我们探究动点问题的依据，从中找到解题的思路和方法，充分挖掘题目中的隐含条件，转化为圆中的相关信息；联想到构造辅助圆的一些基本要素，画出隐藏的圆.

二、实际运用

1.求解定值

例1如图7，直径AB，CD的夹角为60°，P为⊙O上的一个动点（不与点A，B，C，D重合）.PM，PN分别垂直于CD，AB，垂足分别为点M，N.若⊙O的半径长为2，则MN的长（）.

（D）随点P运动而变化，没有最值

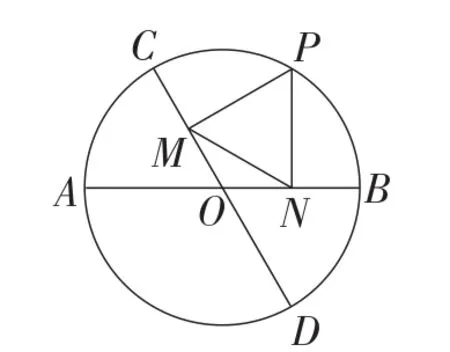
图7

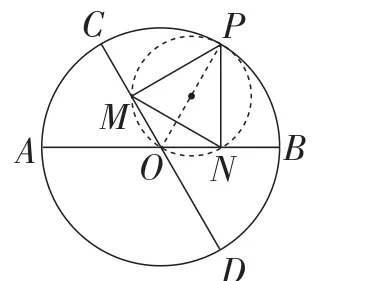
图8

解析：如图8，连接OP，OP=2，

由条件知，∠PNO=∠PMO=90°.

所以O，M，P，N四点共圆.

由直径AB，CD的夹角为60°，可知∠MPN=60°.

圆的半径一定，60°的圆周角所对的弦长是定值.

故选B.

【评注】由基本图形5，找到O，M，P，N四点共圆，即找到共斜边的直角三角形隐藏的外接圆是解题的关键.

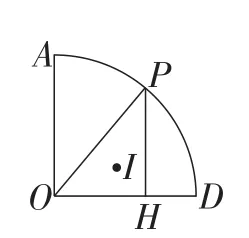
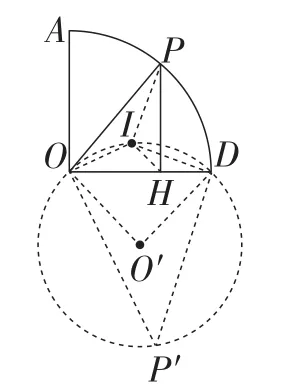
图10

解析：如图10，连接OI，PI，DI，

由△OPH的内心为点I，可得∠PIO=135°.

易证△OPI≌△ODI.

得到∠DIO=∠PIO=135°.

过D，I，O三点作⊙O′，连接O′D，O′O，

所以点I在以OD为弦，并且所对的圆周角为135°的一段劣弧上.

在优弧上取点P′，连接P′D，P′O，

可得∠DP′O=45°.

所以∠DO′O=90°.

故选D.

【评注】这道题利用内心的定义和三角形的全等求出∠DIO=135°，∠DIO所对的边OD=6是定值，在一个三角形中，定长的边长对应定值的内角，则存在一个隐圆，圆的半径是定值，画出隐圆，利用圆周角定理和勾股定理求出半径.

2.求解最值

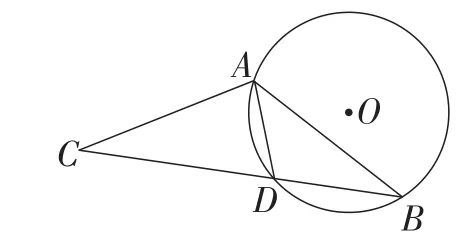
图11

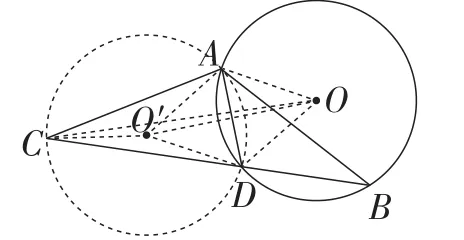
图12

解析：如图12，连接OA，OD，

则△OAD为等边三角形，边长为半径1.由题意可知，∠ACB=∠ABC=∠AOD=30°.

作过点A，D，C的⊙O′，连接O′A，O′D，

（1）∠ACD=30°.

因为∠AO′D=2∠ACD=60°，

则△O′AD也是等边三角形，边长为半径1.

求得∠AO′D=60°，此时点C在劣弧上运动.

所以点C在半径为1的⊙O′上运动.

由点和圆的位置关系可知，当点C，O′，O三点共线时，OC长度取到最大值和最小值，OC长度的取值范围是-1≤OC≤3+1.

故选A.

【评注】这道题将动点B转化到动点C上，在△ABC中，动角∠ACD=30°或∠ACD=150°是一个定角，所对的边AD=1是一个定值，利用基本结论，存在一个隐圆，圆的半径是定值，求最值的问题就转化成圆外一点到圆上一点的最值问题.

例4（2015年湖北·武汉卷）如图13，△ABC，△EFG均是边长为2的等边三角形，D是边BC，EF的中点，直线AG，FC相交于点M.当△EFG绕点D旋转时，线段BM长的最小值是（）.

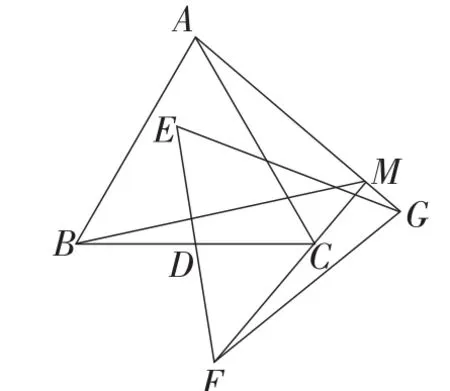
图13

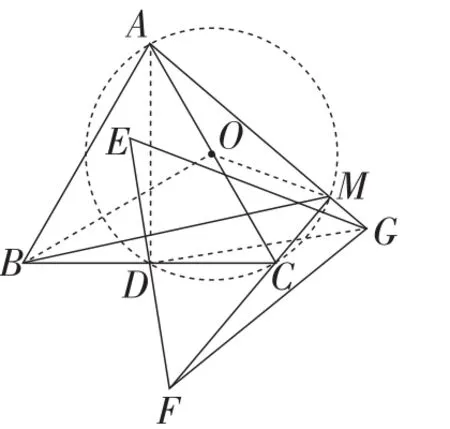
图14

解析：如图14，取AC的中点O，连接AD，DG，BO，OM.

所以△DAG∽△DCF.

则∠DAG=∠DCF，∠DAG+∠DCM=∠DCF+ ∠DCM=180°.

所以A，D，C，M四点共圆，AC的中点O即是圆心，半径为AO=1，画出隐圆⊙O.

当点M在线段BO与该圆的交点处时，线段BM最小，此时，OB=3，OM=1.

故选D.

说明：∠DAG=∠DCF也可以直接根据三角形的内角和为180°得出.

【评注】看似无圆，实则有圆，化隐为显，转换推演，确定动点的运动规律.求最值的问题就转化成圆外一点到圆上一点的最值问题.因此，掌握好方法，动点定下来.

3.求解动点的运动路径长

例5如图15︵，扇形OAB的圆心角的度数为120°，半径长为4，P为上的动点，PM⊥OA，PN⊥OB，垂足分别为点M，N，D是△PMN的外心.当点P运动的过程中，点M，N分别在半径上做相应运动，从点N离开点O时起，到点M到达点O时止，点D运动的路径长为（）.

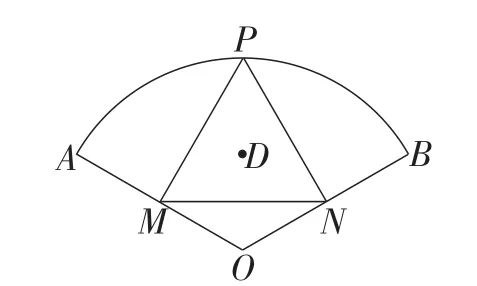
图15

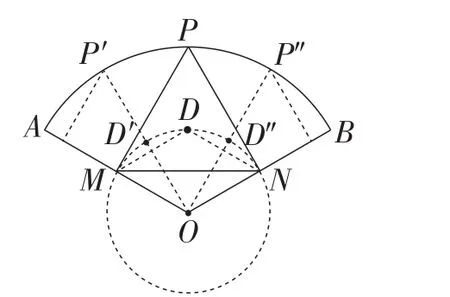
图16

解析：解决此题的关键是找到动点D的运动轨迹.

如图16，连接MD，ND，

由已知条件可知，点P，M，O，N四点共圆，圆心是点D，直径为OP=4.

则∠P=60°.

由定角对定长的三角形隐藏的外接圆可知，点D在△DMN的外接圆上运动.

由圆中的基础知识画出外接圆⊙O，半径OD=2.

故选A.

我们通过画出几何问题中隐藏的圆，即构造辅助圆来解决动点问题，可以为解题带来方便，方法巧妙而独特.当然此类问题也可以用几何问题代数法或是解析法来解决，但运算量较大，较复杂.对于直线型辅助线难以解决，或解答起来较麻烦的几何问题，可以考虑化“隐”为“显”，构造辅助圆来解决.

三、教学启示

在平时的教学中，我们要重视教材，欣赏教材，利用教材，同时又高于教材.对教材的基础知识、基本结论、基本图形、基本方法进行深入研究.在挖掘内涵，拓展结论的过程中，找到动点问题的源头，发现最值问题的根本，总结出一般性的方法，即对此类问题的通用解法.通过找出几何图形的隐圆来确定动点的运动规律，做到“掌握方法，举一反三，通一类题”.这样才能让学生弄清问题的本质，切实有效地提升学生的解题能力，发展学生的思维水平，进而提升成绩.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］胡春洪.例谈“隐圆问题”［J］.数理化解题研究，2014（1）：9.

［3］李玉荣.勾画“隐圆”，破解最值［J］.中学数学杂志，2015（8）：56-58.

［4］王少华.再探利用“隐圆”，破解最值问题［J］.中学数学杂志，2016（6）：65-66.

2017—03—16

王少华（1982—），男，中学一级教师，主要从事中学数学研究.