基于风速相关性风电场储能容量配置定量研究

龚智敏，吴政球，冯闯，邹卫卫

(1.国网淮南供电公司，安徽淮南212007；2.湖南大学电气与信息工程学院，湖南长沙410082；3.国网温州供电公司，浙江温州325000)

基于风速相关性风电场储能容量配置定量研究

龚智敏1，吴政球2，冯闯1，邹卫卫3

(1.国网淮南供电公司，安徽淮南212007；2.湖南大学电气与信息工程学院，湖南长沙410082；3.国网温州供电公司，浙江温州325000)

为研究风速相关性对风电场储能容量的影响，首先建立了风速ARMA模型，并根据时移技术得到风电机组风速分别呈高度、中度和低度三种不同相关度的风电场的风速时间序列，最后对不同相关度下的风电场的储能容量进行定量分析。结果表明，合理布置风电场能在较好利用风能的情况下有效减少风电储能成本和土地资源的浪费。

风速相关性；储能容量；ARMA模型；土地资源

风能作为一种清洁的可再生能源，越来越受到世界各国的重视。2011年底，我国风电并网装机容量4 505万千瓦，装机规模跃居世界第一，2011年风电发电量732亿千瓦时，分别占全国电力装机容量的4.27%和总发电量的1.55%。然而，随着我国风力发电在电网中的比重不断提高，风电并网稳定性问题和储能装置的高成本却使我国风电发展陷入了尴尬境地。

近年来，许多学者对风电场储能容量做了大量研究，文献[1]研究了储能容量的合理范围，文献[2]研究了储能系统的功率和容量配置，文献[3]研究了平抑风电场功率波动的储能容量选取方法，但是这些文献中均没有考虑风速相关性与储能容量的具体定量关系。

由于风电场的占地面积很大，而具有良好风电资源的土地资源是非常宝贵的不可再生资源，从长远发展来看，充分利用风能资源的同时经济、合理地减小风电场面积必将成为风电事业发展中重要的研究课题。然而，随着风电场群占地面积的减小，风电场间的地理位置比较靠近时，风电场基本处于同一风带，其风速具有比较强的相关性[4]。风电场间风速的相关性表征各风电场在同一时刻的出力特性，当相关性较强时，风电场输出的功率波动性较大，此时配置的储能容量也较大，因此关于风速相关性对风电场储能容量的定量分析具有非常重要工程实践意义。

针对以上问题，本文通过对不同相关度下风电场输出功率进行傅里叶曲线拟合，定量分析了风速相关性对于风电场储能容量的重要影响。

1 风速相关性

1.1 风速的ARMA模型的建立

自回归滑动平均模型(ARMA)是目前最常用的拟合平稳时间序列的模型[5]，由因变量对它的滞后值以及随机误差项的现值和滞后值得到。风电场的风速具有时变性，可以视其为一个时间序列，用ARMA(p，q)模型对其进行拟合。ARMA(p，q)模型的基本形式为：

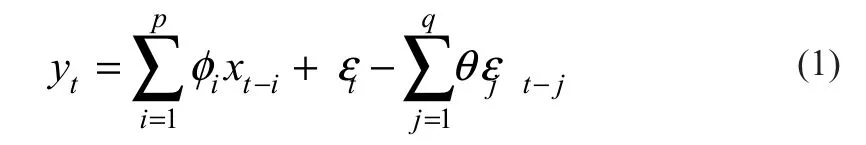
式中：yt为时刻时间序列的值；φi和θj分别为自回归系数和滑动平均系数；εt是白噪声序列，εt～N(0，σt2)，σt为风速测量值的标准差。

根据某地区风速实测数据建立ARMA(1，2)模型如下：

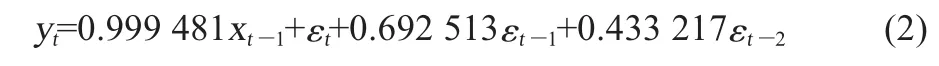
式(2)是均值为0，标准差为1的时间序列，t时刻的5 min级风速时间序列vt可由μt、σt和时间序列yt表示为：

式中：μt为风速测量值的均值，σt为风速测量值的标准差。

1.2 不同相关度的风速时间序列

利用时移技术产生新的风速时间序列[6－7]：

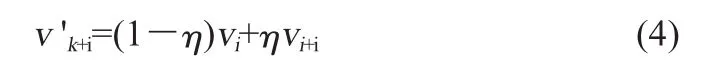
式中：当i+1＞n时，i+1=i+1－n；T=k+η，k为整数，0≤η＜1。

从图1可见，可以利用时移技术产生与原序列相关系数在－1～1范围内任意值的新的风速时间序列。为了分析风电场储能容量与风速相关性的关系，本文以T=0处风电场为参考风电场，分别计算T=5、13和30时新的风速时间序列，得到新的风速时间序列曲线分别如图2～图4所示。

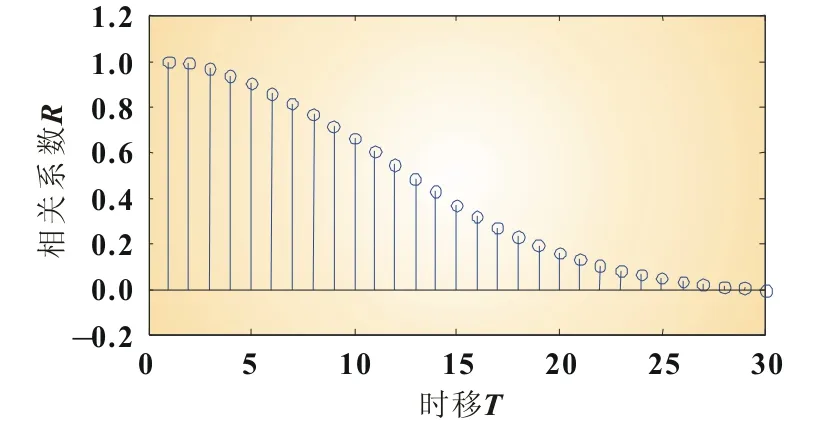
图1 风速时间序列的相关系数

图2 T=5时新的风速时间序列

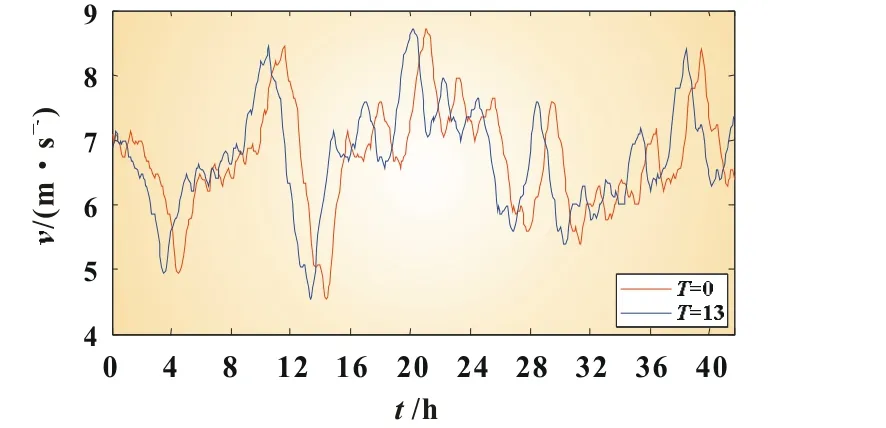
图3 T=13时新的风速时间序列

新的风速时间序列与原风速时间序列的相关系数为：

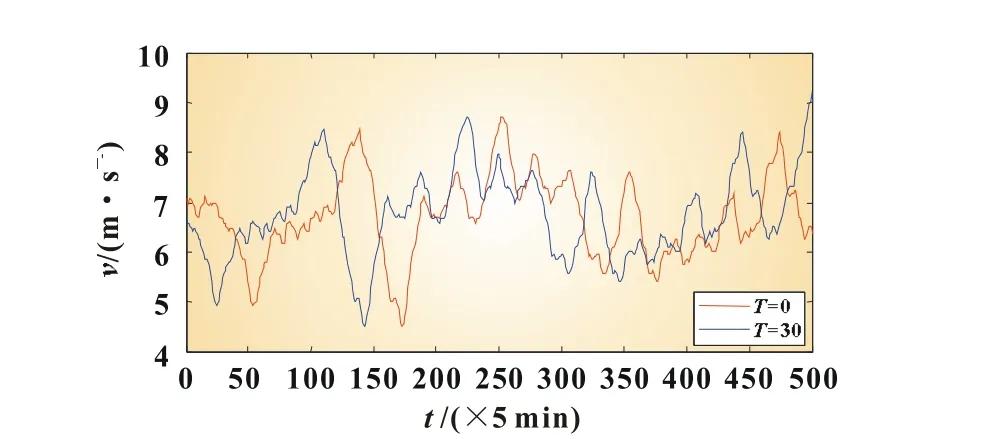
图4 T=30时新的风速时间序列

根据式(5)计算可得：T=5时，新的风速时间序列与原风速时间序列v0的相关系数为0.903 2，此时它们具有高度相关性；T=13时，新的风速时间序列与v0的相关系数为0.488 6，此时它们中度相关；T=30时，新的风速时间序列与v0的相关系数为－0.002 1，此时它们低度相关。由图2～图4可见，随着风速相关度逐渐减弱，新的风速时间序列跟随原序列变化步调逐渐不同步。

1.3 不同风速相关度下风电场间的距离

风电场与参考风电场的距离：

式中：v表示该地区风速平均速度。根据风速实测数据计算得v=6.719 06 m/s。

由式(6)得，风速与参考风电场处风速分别呈高度、中度和低度相关处的风电场与参考风电场的距离如表1所示。

表1 不同风速相关度下风电场与参考距离 m

2 不同风速相关度下风电场的功率计算

本文采用Vestas V90-2.0MW机型的技术参数及功率特性曲线来计算不同相关度风速时间序列的风电场输出功率。Vestas V90-2.0MW机型的切入风速、额定风速和切出风速分别为4、12和25 m/s[8]，用式(7)近似描述风电机组的输出功率与风速的关系[9]：

此时计算不同相关度下的风电场输出功率，得到功率时间曲线如图5所示。由图5可见当风速相关度越高时，风电场总的输出功率波动越大。当风电场场址地域相近时，它们处于同一风带，风速的相关性比较大，导致风电场群总的功率输出波动较剧烈，因此定量分析风电场风速相关性对于研究风电场并网十分必要。

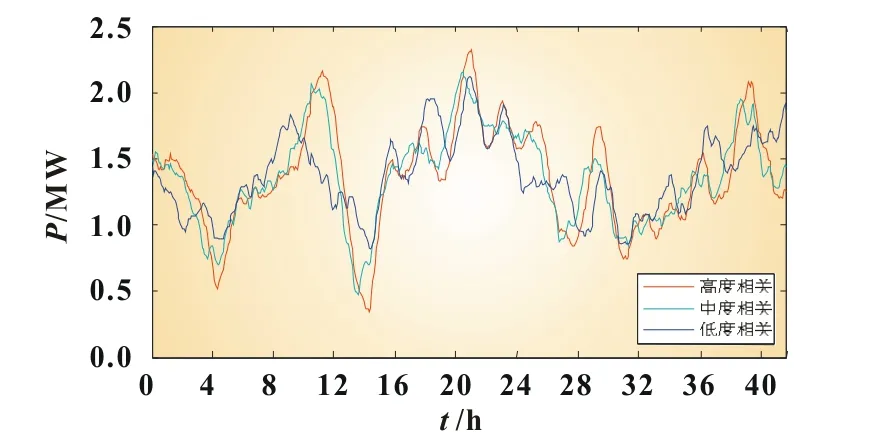
图5 不同风速相关度风电场输出功率

3 储能容量配置

我们以抑制风电场有功功率波动为目的，以风电场可利用风能的平均值为优化目标，优化选取储能装置容量，尽可能平滑风电场的输出功率，减小风电场输出功率的波动[10]。本文用傅里叶曲线对高度相关、中度相关和低度相关的风电场的输出功率进行拟合，计算不同风速相关度下风电场所需配置的储能容量。

由于风速具有随机性和间歇性，鉴于其复杂性，可以用傅里叶级数来近似表示为：

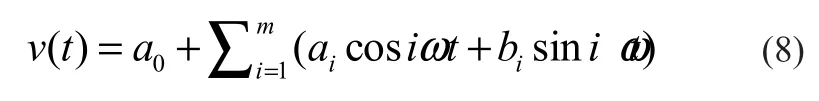
本文假定调度部门合理调度时间为4 h，计算一天24 h的储能容量，利用傅里叶曲线拟合得到16～20 h[即t：192/(5 min)～240/(5 min)]时间段风速低度相关的风电场输出功率拟合曲线如图6所示。

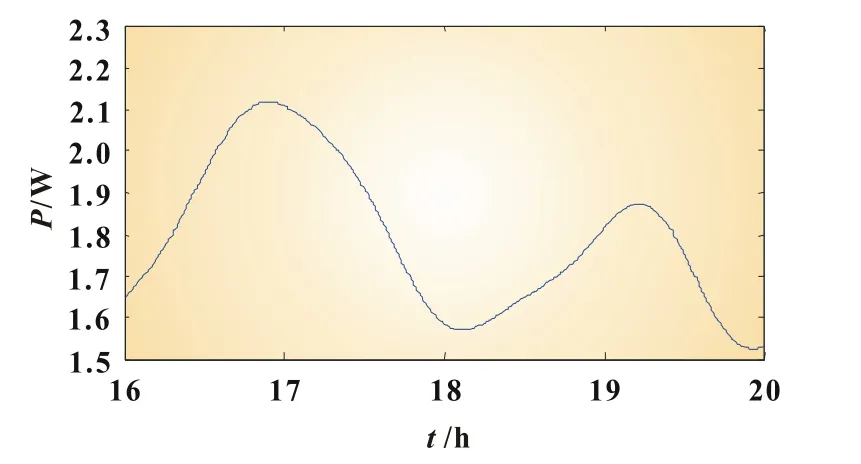
图6 风速低度相关16～20 h风电场功率输出拟合曲线

对应的傅里叶级数如式(9)所示。

对于风电场功率输出曲线函数P(t)，将其平均值E作为整个风电场输出功率的期望。当P(t)＞E时，由储能装置进吸收并存储风电场输出多余部分的能量，以使风电场输出功率始终保持为E；当P(t)＜E时，储能装置则向电网输送功率以弥补风电场输出部分的不足，这样，储能装置就使风电场功率输出平稳，从而减小了风电场并网的压力。为此，我们构造函数f(t)=P(t)－E，f(t)如图7所示。显然有：

式中：m∈N+。f(t)曲线与t轴的上半轴和下半轴所围成面积相等，这里将储能装置容量设置为：

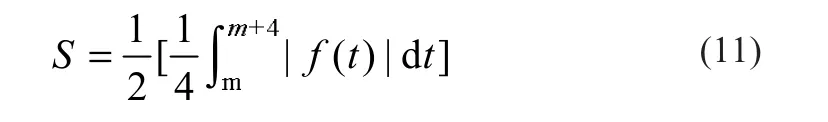
式中：m∈N+。

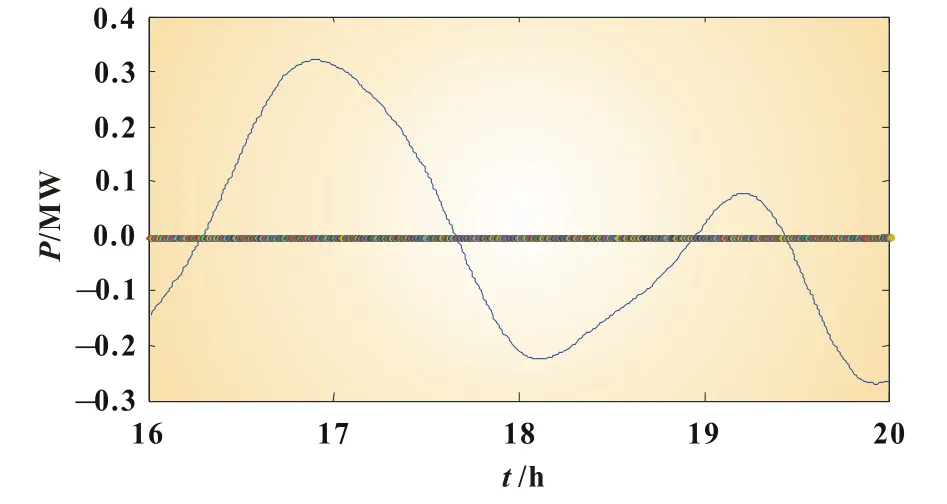
图7 f(t)曲线

把风电场输出功率的傅里叶拟合曲线的平均值作为风电场输出功率的期望值。经计算得风电低度相关时风电场功率输出期望E=1.794 1 MW，风电场所需配置的储能容量为S=0.302 1 MWh。

用傅里叶拟合法求得不同风速相关度风电场的储能容量配置值如表2所示。

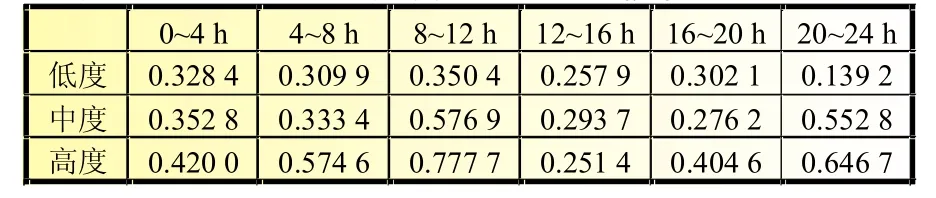
表2 不同风速相关度风电场的储能容量 MWh

从表2可见，在各个时间段，风速相关度对风电场储能容量的影响很明显，风速相关的度较低的风电场所需配的储能容量基本小于风速相关度较高的风电场所需配置的容量。

由表1和表2可见，选择风速中度相关布置风电场比较合适，与风度低度相关风电场相比减少了储能成本，与风度高度相关风电场相比节省了土地资源。

4 结论

风电场风机间距过大时会造成土地资源浪费和管理不便，风电机组距离过小，使得风电场配置的储能成本增加，合理选择风电机组的距离对于节省土地资源和风电场建设的经济性具有十分重要的意义[11]。

此外，如果在合理的风电场布置范围内储能成本仍然不能满足风电发展的要求，一方面可以采取适当的经济措施来“削峰填谷”，例如可以对高耗能企业实施可中断符合，鼓励“有序用电”，使用节能产品；另一方面，采用电力系统稳定器(PPS)技术提高系统的稳定性。

[1]卢继平，朱三立，韩涛，等.风电场储能容量合理取值范围分析[J].重庆大学学报，2010，33(8)：46-51.

[2]文艺，张步涵，毛承雄.风电场中储能系统的功率和容量优化配置[J].湖北工业大学学报，2012，27(1)：18-21.

[3]李文斌，卢继平，徐兵，等.平抑风电场功率波动的储能容量选取方法[J].华东电力，2012，40(3)：440-443.

[4]WAN Y H，MILLIGAN M，PARSONS B.Output power correlation between adjacent wind power plants[J].Journal of Solar Energy Engineering，2003，125：551-555.

[5]张树京，齐立心.时间序列分析简明教程[M].北京：北方交通大学出版社，2003.

[6]范荣奇，陈金富，段献忠，等.风速相关性对概率潮流计算的影响分析[J].电力系统自动化，2011，35(4)：18-22.

[7]XIE K G，BILLINTON R.Considering wind speed correlation of WECS in reliability evaluation using the time-shifting technique[J]. Electric Power Systems Research，2009，79(4)：687-693.

[8]于大洋，韩学山，梁军，等.基于NASA地球观测数据库的区域风电功率波动特性分析[J].电力系统自动化，2011，35(5)：77-81.

[9]宋曙光.风电功率波动特性及其与储能协调策略的研究[D].山东：山东大学，2011.

[10]于慎航.风电场储能容量计算及虚拟储能技术研究[D].山东：山东大学，2011.

[11]张钧.风电场微观选址与总图运输设计优化[J].武汉大学学报：工学版，2011，44(Z)：1-5.

Study on wind field energy storage capacity considering wind speed correlation

GONG Zhi-min1，WU Zheng-qiu2，FENG Chuang1，ZOU Wei-wei3
(1.State Grid Huainan Power Supply Company,Huainan Anhui 212007,China;2.School of Electrical and Information Engineering,Hunan University,Changsha Hunan 410082,China;3.State Grid Wenzhou Power Supply Company,Wenzhou Zhejiang 325000,China)

In order to analyze the effect of wind speed correlation on wind field energy storage capacity,the ARMA model of wind speed time series(WSTS)was built;the time-shifting technique was used to produce three wind speed time series in three different fields in different correlation degrees(high,moderate and low)with the initial WSTS;the energy storage capacity of three wind farms was calculated.The results indicate that the rational layout of the wind farm can not only be useful for efficient utilization of wind energy,but also effectively reduce the energy storage cost and the waste of land resource.

wind speed correlation;energy storage capacity;autoregressive moving average(ARMA)model;land resource

TM912

A

1002-087X(2017)05-0810-03

2016-10-25

龚智敏(1988—)，女，湖北省人，硕士，主要研究方向为风力发电及其并网技术；吴政球(1963—)，男，湖南省人，教授，博士生导师，主要研究方向为电力系统分析与控制、电力市场及分布式发电及其并网等理论研究与工程实践。