能量回馈型超声波电机定子振动特性有限元分析与特性测试

王光庆， 徐文潭， 杨斌强， 陆国丽

(浙江工商大学信息与电子工程学院， 浙江 杭州 310018)

能量回馈型超声波电机定子振动特性有限元分析与特性测试

王光庆， 徐文潭， 杨斌强， 陆国丽

(浙江工商大学信息与电子工程学院， 浙江 杭州 310018)

提出一种集精密驱动和振动能量采集于一体的新型多功能压电振动电机——能量回馈型超声波电机，设计了电机夹心式内锥面压电定子，建立了电机压电定子的有限元模型，仿真分析定子振动特性和能量采集输出特性；研制电机原理样机，并对电机进行阻抗和能量采集特性测试与分析。研究结果为工作在极端封闭环境中的微型机器人系统提供一种集驱动与供电一体化的机电器件。

超声波电机； 振动特性； 能量采集； 有限元方法； 特性测试

1 引言

超声波电机驱动是利用压电陶瓷在高频高压的交变激励电压作用下产生的微幅振动，经过金属弹性体的放大后，通过摩擦驱动与之相接触的转子(或动子)产生旋转或直线运动。由于超声波电机定子振动幅值一般比较小，通常只有微米级别，所以容易实现对转子的精密驱动和定位功能；此外，超声波电机还具有低速大力矩、断电自锁和结构简单等诸多优点，它已广泛应用于航空航天、精密机械、仪器仪表、医疗设备和工业自动化等领域。

目前，超声波电机研究主要集中在结构优化设计[1-3]、数学模型[4-6]和驱动控制[7,8]等问题，并取得了丰富的研究成果。但从功能来看，多数功能单一，主要用来对被控机构提供驱动力或力矩，这将严重影响超声波电机在一些特殊环境中的应用，例如，在一些极端、恶劣、封闭的工作环境(如封闭有毒气体、液体储存罐的检测、高低温等)中的微型机器人，其机械手关节的运动大多采用超声波电机驱动与控制实现。但这些机器人多数采用电化学电池供电，一旦电池能量源耗尽，微机器人也就失去工作能力。

为此，本文提出了一种集压电驱动与振动能量采集于一体的新型多功能压电振动电机——能量回馈型超声波电机，利用压电陶瓷的逆压电效应实现电机的精密驱动功能，利用压电陶瓷的正压电效应采集电机定子在运行过程中的振动能量，并转换成电能，从而给微型机电系统提供电能，该电机突破了现有超声波电机功能比较单一的局限。此外，从能量采集回收角度看，当前主要的能量采集器结构是基于压电单晶或压电双晶的悬臂梁式结构，这种结构主要用于采集电子器件工作环境中的低频振动能量。而能量回馈型超声波电机主要采集压电定子运行过程中的超声振动能量，突破了传统压电振动能量采集器主要采集环境中的低频振动能量的局限。

本文针对提出的能量回馈型超声波电机，设计了电机夹心式内锥面压电定子，利用有限元方法建立了电机定子的有限元机电耦合分析模型，仿真分析了电机定子振动特性和能量采集输出特性，实验测试了电机定子阻抗特性和能量采集转换特性。研究成果为能量回馈型超声波电机的优化设计和控制提供理论和实验依据，也为工作在极端封闭环境中的微型机器人系统提供了一种集驱动与供电一体化的机电设备，具有重要研究意义和实际应用价值[4，5]。

2 能量回馈型超声波电机结构

本文提出的能量回馈型超声波电机的结构原理如图1所示，电机结构借鉴目前主流环形行波型超声波电机结构，由夹心式内锥面定子、锥面转子、底座、端盖和输出轴构成。电机总体结构如图1(a)所示。夹心式内锥面定子结构如图1(b)所示，其主要由激励压电陶瓷、采集压电陶瓷、定子基体和定子齿四部分构成，激励压电陶瓷和采集压电陶瓷分别粘结在定子基体的底部和顶部外侧，构成夹心式压电复合环状结构；在定子基体顶部内侧为内锥面定子齿。激励压电陶瓷是利用逆压电效应将高频高压的交变激励电压转换成定子的微幅振动，并在定子内部产生行波波形，因此，其极化分区模式采用典型行波型超声波电机陶瓷的极化分区模式，激励压电陶瓷极化分区模式如图1(c)所示。采集压电陶瓷则是利用正压电效应将电机定子在稳定运行过程的振动能量采集并转换成电能，为了能最大化地采集定子振动能量，将压电陶瓷均匀分区成18个扇区，每个扇区沿周向的大小恰好与激励压电陶瓷每个扇区的大小相同，相邻两扇区的极化方向相反，采集压电陶瓷极化分区模式如图1(d)所示。在粘结两压电陶瓷时，尽量保证激励压电陶瓷和采集压电陶瓷的扇区在定子基体上要一一对应，即激励压电陶瓷的“+”、“-”极化区分别与采集压电陶瓷的“+”、“-”极化区关于定子基体对称。

图1 能量回馈型超声波电机结构原理图Fig.1 Schematics of new motor

3 电机定子有限元模型

将图1(b)所示的夹心式内锥面定子划分成90单齿，建立其六面体八节点有限元模型，如图2所示。图2所示的有限元实体模型中，基座、支撑、定子齿和定子基体采用8节点线性结构Solid45单元类型建模；激励压电陶瓷和采集压电陶瓷采用8节点6面体耦合场Solid5单元类型建模。压电陶瓷与定子基体之间的胶黏层和压电陶瓷表面电极由于厚度很小，采用Shell63单元类型建模。电机定子有限元网格模型如图3所示。图3所示定子网格模型中，分别对激励压电陶瓷和采集压电陶瓷中电极的各个面进行节点耦合，耦合点设置为电压自由度，与定子基体相连的压电电极耦合成一个参考点，其参考电势设置为零，即参考地。激励压电陶瓷A区电极的节点电压自由度耦合为通用节点“V1”，B区电极的节点电压自由度耦合为通用节点“V2”。采集压电陶瓷分成18个扇区，每个扇区压电陶瓷电极的节点电压自由度耦合为一个通用节点，分别用“V3”，“V4”，…，“V20”表示，如图1(d)所示。

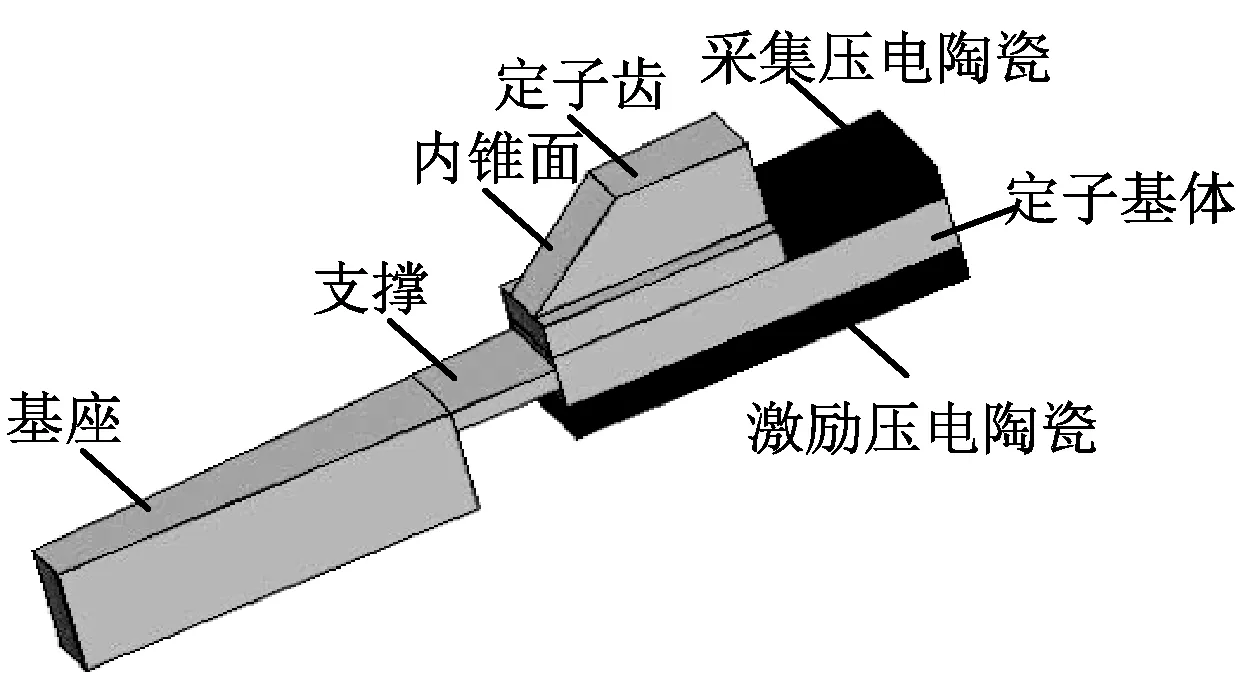
图2 电机定子单齿有限元实体模型Fig.2 Finite element model of motor stator

图3 电机定子有限元网格模型Fig.3 Grid model of motor stator

4 仿真分析

用于电机定子仿真分析的结构尺寸和材料参数如表1、表2和图4所示。

4.1 定子振动模态分析

给图3所示的定子有限元模型内圈(半径为R3)表面加上位移约束，用Lanczos方法计算得到电机定子的振动模态，如图5所示。本文电机工作模态为B09模式，由图5计算得到的定子振动模态可以看出，定子B09模态的振动频率为39.72kHz，定子最大振幅发生在定子外圈，即采集压电陶瓷所处位置，这有利于采集压电陶瓷产生较大的变形，从而提高其振动能量采集性能；另外，定子锥面的振动幅值比较均匀，这有利于提高电机运行的平稳度，减小噪声。

表1 定子结构尺寸

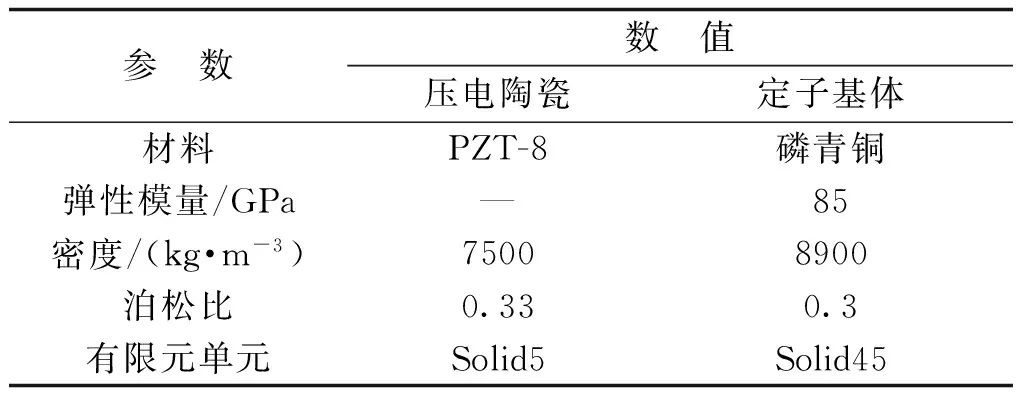
表2 定子材料参数

图4 电机定子尺寸示意图Fig.4 Sizes of motor stator

图5 定子B09振动模态Fig.5 B09 mode of motor stator

4.2 谐响应特性分析

在通用节点“V1”与参考地以及通用节点“V2”与参考地之间分别施加幅值为Vm=100V正弦激励电压，对电机定子进行谐响应分析。Ansys分析计算中定子结构阻尼采用Rayleigh 阻尼。

定子谐响应分析计算中所取节点示意图如图6所示，其中节点“10”和“20”分别为激励压电陶瓷表面节点；节点“30”、“40”、“50”和“60”分别为定子齿顶部节点；节点“70”和“80”分别为定子齿锥面节点；节点“90”、“91”、“92”、“93”、“94”和“95”分别为激励压电陶瓷底面节点。

图6 定子节点示意图Fig.6 Nodes distribution of motor stator

依次从采集压电陶瓷表面外圈至定子锥面底部的定子节点“10”，“20”，…，“80”的x向振动位移幅值和相位响应仿真曲线如图7所示，对应节点y向振动位移幅值和相位响应仿真曲线如图8所示，对应节点z向振动位移幅值和相位响应仿真曲线如图9所示。从图7至图9的振动位移幅值响应结果看，定子表面节点的z向振动位移最大产生在定子外圈，即图9(a)中所示的激励压电陶瓷表面节点“10”处，振动幅值达到2.3μm；沿着定子半径递减方向(从定子外圈到内圈)，定子表面节点的z向振动位移幅值逐渐减小，在锥面节点“80”处达到最小值1μm，但节点“30”、“40”、“50”和“60”的z向振动位移幅值减小梯度比较缓和；从图9(b)的相位曲线看，定子表面节点z向振动位移在谐振频率38.4kHz前是完全一致的。定子表面节点的x向和y向振动位移幅值最大值均产生在定子齿顶表面节点，即节点“30”，“40”，“50”和“60”，并且沿着定子径向方向，齿顶表面节点在这两个方向的振动位移幅值几乎保持恒定，分别达到0.42μm和1.75μm。定子锥面节点“70”和“80”处，x向和y向振动位移幅值较小，但是沿定子径向方向的变化梯度却较大，不利于电机的稳定运行。此外，定子表面节点x向振动位移的相位在谐振频率38.4kHz以前与y向和z向的振动相位相反。总之，定子节点“10”和“20”的z向振动位移幅值大可以提高采集压电陶瓷的振动变形，从而提高其能量采集和转换能力；而节点“30”、“40”、“50”和“60”在x向和y向的振动幅值保持恒定，在z向的振动幅值减小梯度比较缓和，有利于提高电机的运行稳定性，减小电机运行噪声。

图7 定子表面节点x向振动位移幅值响应和相位响应曲线Fig.7 x-direction displacements of stator nodes amplitude response and phase response curves

图8 定子表面节点y向振动位移幅值响应和相位响应曲线Fig.8 y-direction displacements of stator nodes amplitude response and phase response curves

图9 定子表面节点z向振动位移幅值响应和相位响应曲线Fig.9 z-direction displacements of stator nodes amplitude response and phase response curves

定子采集压电陶瓷输出电压幅值和相位响应曲线如图10所示，为节省空间，本文从采集压电陶瓷的18个扇区取相邻5个扇区进行研究，其电压耦合节点分别为“V3”、“V4”、“V18”、“V19”和“V20”，这5个扇区两两相邻，且压电陶瓷极化方向相反(如图1(d)中“+”、“-”所示)。由图10(a)可知，5个压电陶瓷扇区的采集输出电压幅值大小基本一致，在定子谐振频率38.4kHz时达到最大。此外，由于“V3”和“V4”两扇区压电陶瓷极化方向相反，两者采集输出电压的相位在谐振频率38.4kHz以前刚好相差180°。同理，“V18”和“V19”、“V19”和“V20”以及“V20”和“V3”所表示的压电陶瓷扇区极化方向相反，相位响应曲线也相差180°的，这与图1所示的定子陶瓷极化分区模式是相吻合的，同时也验证了能量回馈型超声波电机定子具有行波驱动和振动能量采集功能的有效性和可行性。

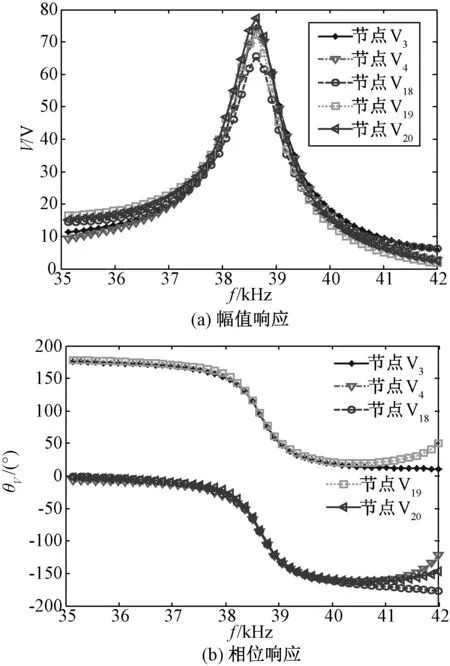
图10 采集电压幅值响应和相位响应曲线Fig.10 Harvesting voltage amplitude response and phase s curves

4.3 瞬态特性分析

分别给激励压电陶瓷A区的电压耦合节点“V1”和B区的电压耦合节点“V2”施加相位差为90°的正弦信号，如下所示：

VA=100sin(2πft)

(1)

VB=100sin(2πft+π/2)

(2)

式中，f=38.4kHz，且将VA和VB每个周期离散成20个子步，电机定子结构阻尼设置为0.05。经有限元计算得到定子齿面各节点振动位移和激励压电陶瓷采集输出电压的瞬态响应特性曲线。

定子采集压电陶瓷片表面中心位置节点在x向、y向和z向的振动位移曲线如图11所示，由图11可知，采集压电陶瓷的振动主要以z向的振动为主，振动位移幅值达到1.75μm，其他两个方向上的振动比较小，大的轴向振动有利于提高采集压电陶瓷的弯曲振动应变，从而提高其能量采集和转换的能力。考虑到各扇区采集输出电压基本一致，本文仅给出V3扇区的采集压电陶瓷输出电压曲线如图12所示。由图12可知，采集压电陶瓷每个扇区采集输出的电压达到52V。

图11 节点20振动位移Fig.11 Displacement of Node No.20

图12 采集输出电压曲线Fig.12 Harvesting voltage curve

定子齿表面质点在x向、y向和z向的振动位移曲线如图13所示，由图13可知，齿表面质点的振动主要以y向和z向为主，这有利于提高电机的机械输出特性。z向振动使定子和转子之间产生一定的压紧力，定子和转子紧密接触形成一个粘弹性接触区；y向振动则使接触区内的定、转子接触质点产生相对滑动，通过摩擦力推动转子运行。从图13可以看出定子齿表面质点在y向和z向的最大振动位移幅值分别为1.06μm和1.27μm。

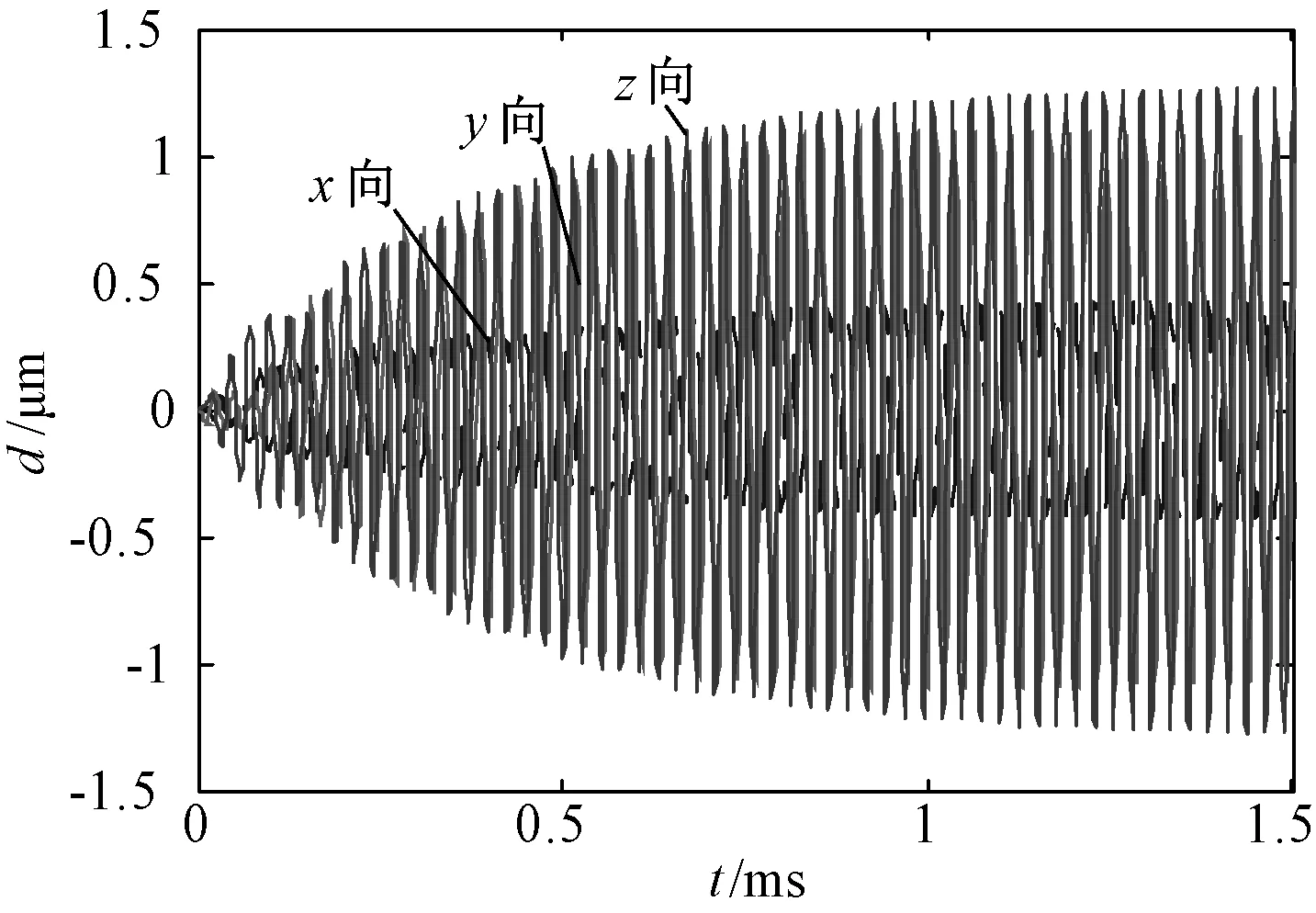
图13 定子齿表面质点振动位移曲线Fig.13 Displacement of top teeth of stator

定子锥面质点在x、y和z三个方向上的振动位移曲线如图14所示，由图7和图14可知，锥面质点x向的振动位移与z向的振动位移是反向的，且两者的合成位移为：

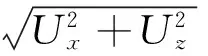
(3)

(4)

式中，Ux和Uz分别为定子锥面质点x和z的振动位移幅值，θ为合成位移与x方向的夹角。若采用锥面驱动方式，为了提高锥面的力传递效率，锥面必须与合成位移U振动方向垂直。

提取定子齿顶质点稳态时x、y和z方向的振动位移，可以得到质点的椭圆运动轨迹，如图15所示。从15图可以看出，定子质点的振动主要在y和z方向，x方向的振动比较微弱，这与图7、图8和图9所示的谐响应特性是一致的，这有利于提高电机定、转子摩擦接触面间的力传递特性，减小定、转子接触面间的径向滑动摩擦磨损，从而提高电机的机械输出性能和能量传递效率。

图14 定子锥表面质点振动位移曲线Fig.14 Displacement of cone node of stator

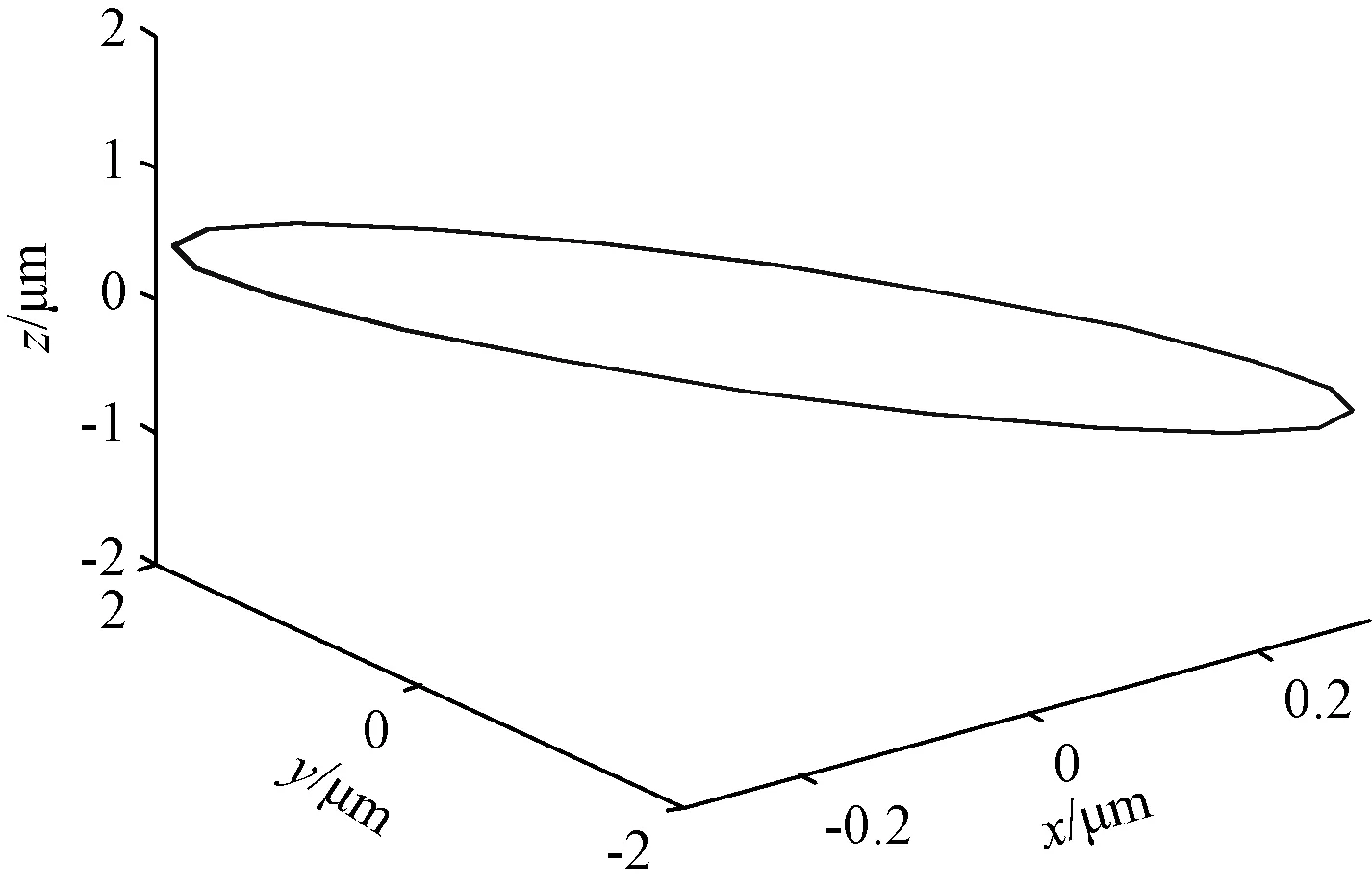
图15 定子齿质点椭圆轨迹Fig.15 Elliptic orbit of the stator teeth

由图11～15可知，电机定子振动在1.5ms时就进入了稳定振动状态，说明电机具有较快的响应特性。同时，也验证了能量回馈型超声波电机的设计构想是正确可行。

5 样机及特性测试

根据有限元设计和分析得到的电机结构尺寸，制作加工了能量回馈型超声波电机原理样机，如图16所示。利用阻抗分析仪对样机进行阻抗特性测试(预压力F=0时)，电机阻抗实验结果如图17所示，由实验结果可以看出样机的谐振频率为37.6kHz，与有限元结果38.6kHz误差1kHz，这主要是样机制作过程中零件尺寸加工误差所致。考虑预压力的影响，电机谐振频率增大到38.5kHz，与有限元结构基本一致。单个采集压电陶瓷扇区的能量采集输出功率实验结果如图18所示，由图18可知，在最佳匹配阻抗条件下，采集压电陶瓷的输出功率达到最大0.44W。能量回馈型超声波电机与传统行波型超声波电机能量组成实验对比结果见表3，实验比较是两电机在相同的驱动电压和驱动频率激励作用下进行的，表3中有用输出功率是指电机转子输出功率。由表3的实验对比结果可以看出，能量回馈型超声波电机的能量使用效率大大提高了。传统行波型超声波电机输入能量中除了小部分(4.5W)被传递到转子作为有用输出功率外，大部分都被损耗掉了，其能量使用效率仅为20%。而能量回馈型超声波电机中除了有用输出功率4.5W外，通过采集压电陶瓷转换输出的有用功率达到了7.92W，使得电机的能量使用效率提高到54.7%。

图16 能量回馈型超声波电机原理样机Fig.16 Prototype of new motor

图17 电机阻抗实验结果Fig.17 Experimental impedance results of motor

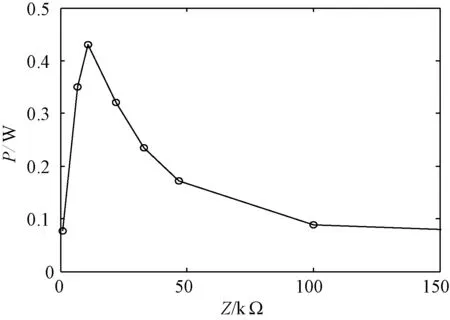
图18 单个扇区采集输出功率实验结果Fig.18 Harvesting power experimental result of a sector

参 数数 值传统行波型电机规格Φ60能量回馈型电机规格Φ60输入功率/W22.522.5有用输出功率/W4.54.4采集回收功率/W—7.92*损耗功率/W1810.18能量使用效率(%)2054.7

注：*表示每个采集压电陶瓷扇区在最佳匹配阻抗前提下，18个采集压电陶瓷扇区并联得到的采集输出功率实验结果。

6 结论

本文提出了一种新型多功能压电振动电机——能量回馈型新型超声波电机，通过对电机的结构设计、有限元分析及其特性测试，得到以下结论：

(1)设计的能量回馈型超声波电机的工作频率为38.6kHz，其能量使用效率达到54.7%。

(2)采用内锥面夹心式压电定子结构可以使齿定面质点振动位移的均匀得到改善，提高电机输出性能的稳定性。

(3)采集压电陶瓷粘结于压电定子上表面外圈，有利于提高电机振动能量采集器输出电压。

(4)采用内锥面驱动转子时，定转子接触面需与锥面质点轴向和径向振动位移的合成位移方向垂直。

研究结果表明能量回馈型超声波电机的构思是可行的，有助于为极端环境中工作的微机电系统提供了一种集驱动与供电的新方法。

[1] Mohd Romlay F R, Wan Y W, Mat Piah K A. Increasing the efficiency of traveling wave ultrasonic motor by modif-ying the stator geometry [J]. Ultasonics, 2016, 64:177-185.

[2] Yang Xiaohui, Liu Yingxiang, Chen Weishan, et al. A cylindrical traveling wave ultrasonic motor using bonded-type composite beam [J]. Ultasonics, 2016, 65:277-281.

[3] Peng Taijiang, Wu Xiaoyu, Liang Xiong, et al. Investigation of a rotary ultrasonic motor using a longitudinal vibrator and spiral fin rotor [J]. Ultrasonics, 2015, 61:157-161.

[4] Lu Xiaolong, Hu Junhui, Yang Lin, et al. A novel in-plane mode rotary ultrasonic motor [J]. Chinese Journal of Aeronautics, 2014, 27(2):420-424.

[5] 王瑞霞, 金龙, 潘鹏，等(Wang Ruixia, Jin Long, Pan Peng, et al.). 一种方底座短柱状超声波电机的设计(A short cylindrical ultrasonic motor with square base)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(2):134-139.

[6] 王剑, 白洋, 郭吉丰(Wang Jian, Bai Yang, Guo Jifeng). 两自由度微型超声波电机的优化设计(Optimum design of two-degree-of-freedom micro ultrasonic motor) [J]. 振动、测试与诊断(Journal of Vibration, Measurement & Diagnosis), 2013, 33(S2):45-48,217.

[7] 傅平, 胡锡幸, 郭吉丰(Fu Ping, Hu Xixing, Guo Jifeng). 二自由度行波型超声波电机定子的优化研究(Optimization research of stator with two degree-of-freedom traveling-wave spherical ultrasonic motor) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(5):30-34.

[8] 陈乾伟, 时运来, 黄卫清(Chen Qianwei, Shi Yunlai, Huang Weiqing). 单模态驱动双向运动的斜动子V形超声电机(Single-mode-drive-type bi-directional linearly moving ultrasonic motor with inclined slider and v-shaped stator)[J]. 南京航空航天大学学报(Journal of Nanjing University of Aeronautics & Astronautics), 2015, 47(1):139-144.

FEM analysis of vibration performance and impedance test of stator of energy harvesting type ultrasonic motor

WANG Guang-qing, XU Wen-tan, YANG Bin-qiang, LU Guo-li

(School of Information and Electronic Engineering, Zhejiang Gongshang University, Hangzhou 310018, China)

A new type piezoelectric vibration motor named energy harvesting type ultrasonic motor was proposed in this article. The mator has the functions of precision actuating and vibration energy harvesting. A sandwich structure stator with an inner cone was designed, and the finite element model of the stator was established. Some simulations were carried out to analyze the vibration performance and the energy harvesting performance, respectively. The results are auned to provide an electromechanical device to power the micro robots which are operating in an extremely environment.

ultrasonic motor; vibration performance; energy harvesting; finite element method; characteristics test

2016-03-15

国家自然科学基金项目(51277165)、浙江省自然科学基金项目(LF15Y010001)

王光庆(1975-), 男, 江西籍, 教授， 博士, 研究方向为超声波电机和压电振动能量采集技术等； 徐文潭(1994-), 男, 江苏籍, 硕士研究生, 研究方向为超声波电机设计及其控制。

TM356

A

1003-3076(2017)06-0047-07