PMI新出口订单指数实证分析

李 娜

(国家统计局 服务业统计司，北京 100826)

PMI新出口订单指数实证分析

李 娜

(国家统计局 服务业统计司，北京 100826)

近年来，我国对外贸易体量不断增大，与全球经济共振现象日益明显，尤其是制造业出口受我国主要贸易伙伴国的经济变动影响更大，为了给政府部门、相关行业和企业制定外向型的政策和经营决策提供参考依据，对制造业新出口订单指数进行了实证分析，以期发挥采购经理指数的预测预警功能。对2005年以来我国制造业新出口订单指数、欧美日PMI和工业企业出口交货值等相关数据进行了时差相关分析、建立了VAR模型，并对工业出口交货值和新出口订单指数进行预测。

PMI；新出口订单指数；出口交货值；VAR模型

一、研究背景与意义

制造业PMI起源于美国二十世纪三十年代，经济学家经过多年的研究，认为其在经济监测、预测和预警中发挥着重要的作用，PMI被认为是可靠的短期经济先行性指标。从国外看，美国学者研究发现，GDP作为衡量国民经济发展情况最重要的一个指标，PMI与GDP具有较高的相关性，且其转折点往往领先于GDP数月；从国内看，PMI与滞后1个季度GDP的相关系数为0.74，相关性较高。如在2008年底金融危机全面爆发之际，我国制造业PMI领先GDP一个季度探明底部和短期反弹顶部。

改革开放以来，中国经济与世界经济高度融合，中国经济与世界经济的关联越来越高。工业制品出口是我国货物出口的重要组成部分，占货物出口总额的95%左右，对我国经济增长的拉动作用明显，受外部需求影响很大。制造业出口研究有助于对我国国民经济发展进行预测和宏观调控，也有利于分析判断国际经济形势。近些年来，随着中国对外贸易体量不断增大，中国在世界经济版图中的地位也不断提升，但国际经济的变动对我国出口的影响也越来越大。特别是2008年金融危机以来，中国的出口与世界经济共振的现象越发明显。因此，进行制造业新出口订单指数的国际对比研究，对宏观经济调控、制定外向型经济政策以及指导出口企业制定生产计划，对我国出口贸易这艘经济巨轮行稳致远，具有重要的现实意义。

二、我国新出口订单指数与欧、美、日PMI变动趋势分析

采购经理指数体系中的新出口订单指数(缩写为CNEX)与欧元区PMI、美国PMI和日本PMI(缩写分别为EUPMI、USPMI、JPPMI)具有非常强的可比性。2005年1月至2008年3月，中国新出口订单指数与主要贸易伙伴国PMI多数位于临界点上方，其中新出口订单指数大多时间高于欧元区PMI和美国PMI。2008年4月至2010年9月，中国新出口订单指数与欧元区、美国、日本PMI均呈探底后反弹的明显的V字型走势，且中国新出口订单指数早于其他三国PMI探底1-2个月，并早于其他三国PMI2-5个月回至临界点以上。2010年10月至2011年7月，欧美发达国家经济处于弱复苏阶段，对外部需求偏弱，造成同期我国新出口订单指数总体低于欧元区和美国PMI；同一时期日本对来自中国产品需求有所加快，所以中国新出口订单指数高于日本PMI，且位于临界点以上，呈平稳波动走势。2011年8月至今，我国新出口订单指数、欧元区和日本PMI大多位于临界点以下，美国PMI明显优于前三者，大多位于50%以上，表明美国制造业有回归迹象，我国出口形势总体来讲不容乐观。

图1 中国新出口订单指数与欧、美、日PMI走势图

三、我国新出口订单指数与其他相关指标的实证分析

(一)时差相关法分析

选择中国新出口订单指数为基准指标，将它与欧元区PMI、美国PMI、日本PMI进行时差相关分析。假设CNEX为Y，被选的三个指标为X，计算Y与X的时滞为k的时间序列之间的相关系数ri(k=0，±1，±2，……)，能使相关系数最大的时滞k，即为该指标的先行或滞后月份。计算公式为：

1.我国工业出口交货值与各国PMI

从我国工业出口交货值与欧元区、美国和日本PMI的时差相关性分析中可以看出，各国PMI对我国的工业出口交货值有一定的先行性(见图2)，其中欧元区与我国工业出口交货值的相关性最优(见表1)。从时差相关分析可以看出，国际市场需求的强弱直接影响我国的外贸情况，且从国外需求产生、发出订单到国内接收订单、形成生产，再到最终的产品运输交付大概有4-6个月的时差，利用国外PMI预测我国的出口情况具有实际经济意义。

表1 我国工业出口交货值与各国PMI的时差相关分析表

图2 欧、美、日PMI与我国工业出口交货值时差相关系数

2.我国新出口订单指数与国外PMI

从我国的新出口订单指数与国外PMI的时差相关分析中可以看出，日本PMI与我国新出口订单指数的相关性最好，最大时差相关系数达到0.751(见图3)，且先行1个月左右。总之，各国PMI与我国新出口订单指数虽然也有较好的相关性，但先行性比较微弱，大概有1个月左右的先行性。

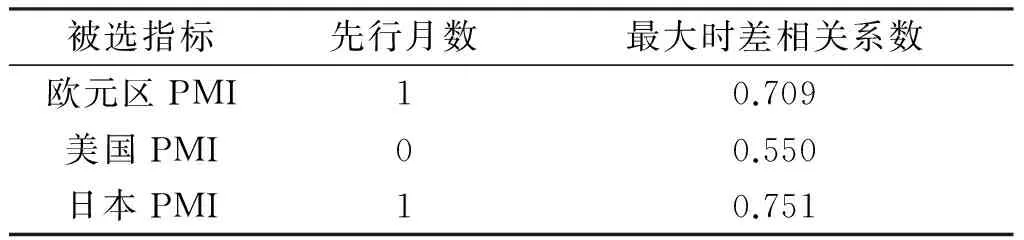
表2 我国新出口订单指数与各国PMI的时差相关分析表

图3 欧、美、日PMI与新出口订单指数时差相关系数

(二)建立向量自回归(VAR)模型

1. ADF单位根检验

ADF单位根检验是运用时间序列进行实证研究的一个重要分析过程。对时间序列的ADF单位根检验即是对序列的平稳性进行检验。对于不平稳时间序列来说，如果存在单位根的情况下，能够运用一阶差分的方法来消除掉单位根，这样就可以得到平稳序列，以进行下一步的实证检验。

表3 相关变量ADF单位根检验表

图4 VAR模型的单位根检验

为了分析数据平稳性，对CNEX、CNExport(工业出口交货值)、EUPMI、USPMI、JPPMI进行了ADF单位根检验，其结果如表3所示。通过检验分析的结果可以发现，CNEX在5%的显著水平下是平稳的，而CNExport、EUPMI、USPMI和JPPMI在 5%的显著水平下都是非平稳的。因此，对 CNExport、EUPMI、USPMI和JPPMI 进行一阶差分处理，处理后的数据D(CNExport)、D(EUPMI)、D(USPMI)和D(JPPMI)均实现平稳,数据一阶单整，可以进行下一步的格兰杰因果检验和分析。

2. 格兰杰因果检验

从Granger因果检验结果可以看出，我国新出口订单指数不是各国PMI的Granger原因的假设均被接受，说明我国新出口订单指数的变化不会引起国外PMI的变化，不是国外PMI变化的原因；而各国PMI不是我国新出口订单指数的Granger原因的假设均被拒绝，说明各国PMI与我国新出口订单指数之间存在一定的协整关系。各国的PMI对我国的出口情况有一定的影响，因此可以使用国外PMI与我国新出口订单指数建立VAR模型。

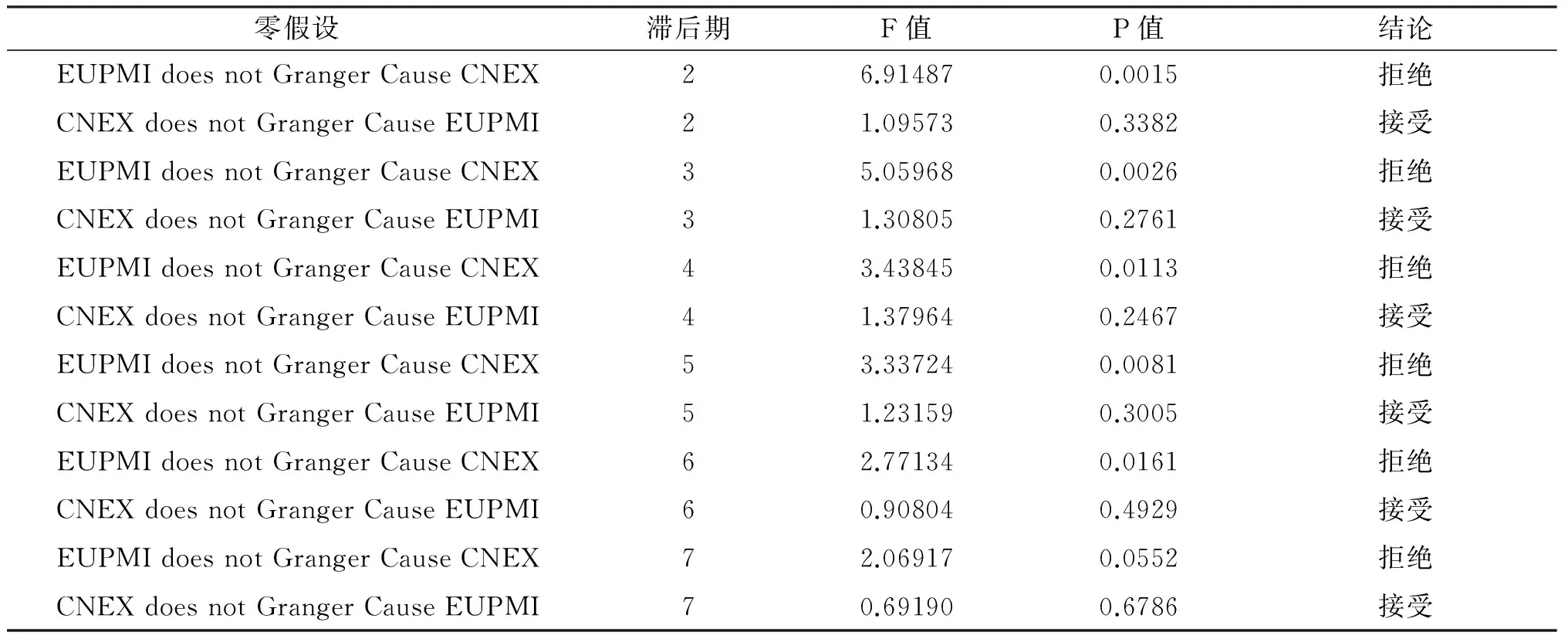
表4 欧元区PMI与中国新出口订单指数Granger因果检验表

表5 美国PMI与中国新出口订单指数Granger因果检验表

表6 日本PMI与中国新出口订单指数Granger因果检验表

3. 滞后阶数的确定

通过上述分析可以得出，数据已经满足了平稳性的条件，接下来要确定滞后阶数。通过以下分析，确定VAR模型的滞后阶数。

表7 相关变量的拟合检验准则

从表7可见，本文根据赤池(AIC)信息准则SC信息准则确定滞后阶数。确定滞后阶数的方法与原则是在增加滞后阶数的过程中，使AIC和 SC值同时最小。通过对我国新出口订单指数和欧元区、美国、日本PMI这些变量逐阶建立VAR模型得出以上信息，根据AIC、SC信息准则、最终预测误差FPE以及LR检验统计量，以“*”标记出依据相应准则选择出的滞后阶数，可以看到，所有准则都选择2为最优滞后阶。因此，下文中建立模型时选择滞后2阶。

4. 脉冲响应分析

脉冲响应函数用于衡量来自某个内生变量的随机扰动项的一个标准冲击( 称之为“脉冲”) 对 VAR 模型中所有内生变量当前值和未来取值的影响。

图5 欧元区、美国、日本PMI对中国新出口订单指数的冲击

从图5可见，欧元区PMI、美国PMI、日本PMI三个指数的扰动项对我国新出口订单指数产生的影响。在分别对CNEX施加来自各国PMI一个标准差的冲击后，结果显示，三个PMI对CNEX产生冲击的趋势是一致的，均为先扬后抑，先为正向影响，在11-13期左右变成负向影响。具体来看，EUPMI对CNEX的扰动冲击最大，前期表现出较为强烈的正向影响，在第二期迅速上升为1.06，并在第三、四期提升至最大值，约为1.76-1.72，从第五期开始后，这种正向影响会随着时期数的增加逐渐减弱，并在第十一期时趋于0，之后均为负向影响，第十五期时负向影响为-0.15，这种冲击的影响将逐渐消失，最终趋于0。USPMI和JPPMI对CNEX的脉冲扰动曲线基本一致，且二者的正向影响远远低于EUPMI，USPMI在第二期时，冲击的影响达到最大，为0.51。JPPMI第三期达到最大，为0.49。随着时间向后推移，这种正向影响逐步减弱，响应较为平缓地下降，但二者与EUPMI相比，持续的时间较长，均在第13期左右趋向0，并在后期出现较弱的负向影响，并最终趋向0。

总之，我国新出口订单指数均明显受到三个PMI扰动的影响，且对来自欧元区PMI的响应较为明显，但正向扰动响应的时期区间略短，而对美国和日本PMI的响应程度略低，但正向扰动响应的时间区间较长。

5. 方差分解

方差分解是通过分析每一个结构冲击对内生变量变化(通常用方差来度量)的贡献度，进一步评价不同结构冲击的重要性。因此，方差分析给出对VAR模型中的变量产生影响的每个随机扰动的相对重要性的信息。

前面利用脉冲响应函数，分析了CNEX对EUPMI、USPMI、JPPMI 扰动冲击变化的响应，下面利用方差分解方法进一步分析EUPMI、USPMI、JPPMI对CNEX变化的贡献度，这里选定的时期数为10期。方差分解结果如图6所示，方差分解数据见表8。

图6 中国新出口订单指数的方差分解图

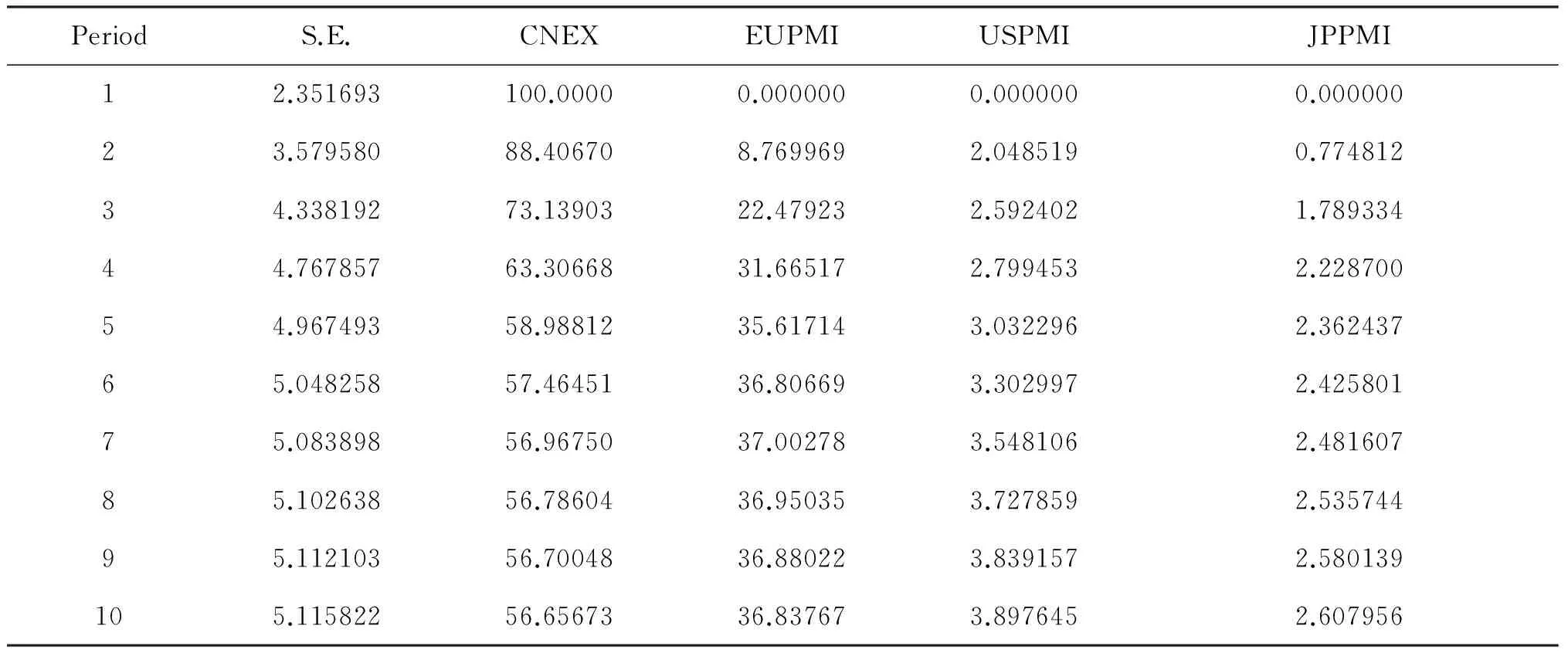
PeriodS.E.CNEXEUPMIUSPMIJPPMI12.351693100.00000.0000000.0000000.00000023.57958088.406708.7699692.0485190.77481234.33819273.1390322.479232.5924021.78933444.76785763.3066831.665172.7994532.22870054.96749358.9881235.617143.0322962.36243765.04825857.4645136.806693.3029972.42580175.08389856.9675037.002783.5481062.48160785.10263856.7860436.950353.7278592.53574495.11210356.7004836.880223.8391572.580139105.11582256.6567336.837673.8976452.607956

Cholesky Ordering: CNEX EUPMI USPMI JPPMI

结合表8的详细参数，再参照图6中的曲线走势，在第一期预测中，CNEX预测方差全部是由自身扰动所引起的。随着时间的推移，CNEX的预测方差中EUPMI、USPMI和JPPMI的扰动贡献率出现增加，而自身的扰动贡献率出现衰减。在第二期预测中，CNEX的预测方差有88.4% 是由自身扰动引起的，有8.8%是由EUPMI引起的，有2.0%是由USPMI引起的，有0.8%是由JPPMI引起的。随后，CNEX预测方差中由非CNEX变量扰动所引起的部分增加，而CNEX自身扰动引起的部分下降，但其所占的百分比还是比较大。大约在第六期左右，CNEX的分解结果基本稳定，CNEX的预测方差有57.5% 是由自身扰动引起的，有36.8%是由EUPMI引起的，有3.3%是由USPMI引起的，有2.4%是由JPPMI引起的。

综上所述，即随着预测期的推移，CNEX方差中由自身扰动所引起的部分的百分比缓慢下降，而由非自身变量扰动所引起的部分的百分比则缓慢增加，并且在预测的第六期左右保持稳定。数据表明，欧元区PMI对我国新出口订单指数的预测误差的贡献度较大，超过35%，而美国PMI和日本PMI对我国新出口订单指数的预测误差的贡献度较小，二者之和大概为6.5%。

(三)自回归滞后模型分析

上文具体研究了各国PMI与我国新出口订单指数的相对稳定关系，下文用自回归滞后模型进行预测，其表达式为：

Yt=β0+β1Yt-1+β2Yt-2+…+β4Yt-q+α0Xt+α1Xt-1+…+α3Xt-3+μt

其中，β0为系统的待估参数，Yt-i是滞后i期的外生变量向量，Xt-i为滞后i期的内生变量向量，且每个外生变量的最大滞后阶数为s阶，αi是向量参数，βi(i=1,…,q)为自回归系数，μt为随机误差项。

1. 我国工业出口交货值增速的预测

根据ADL 模型定义和上文的论述，我国新出口订单指数对工业出口交货值具有一定的先行性，因此首先将我国工业出口交货值作为外生变量，将新出口订单指数作为内生变量，并尝试从一阶滞后开始拟合，根据赤池信息准则AIC和施瓦茨准则SC信息准则，选用ADL(2，2)模型作为选定模型如下：

Exportt=β0+β1Exportt-1+β2Exportt-2+α0CNEXt+α1CNEXt-1+α2CNEXt-2+μt

将历史数据带入上述公式，得到估计结果模型1为：

Exportt=0.924×Exportt-1-0.078×Exportt-2+0.531×CNEXt-0.500×CNEXt-1+0.387×CNEXt-2-19.750

鉴于我国主要贸易伙伴国的PMI的波动对我国工业出口交货值也有一定的影响，接下来使用各国PMI作为内生变量，尝试从一阶滞后开始拟合，并根据最优阶数选取法则，确定模型如下：

Exportt=β0+β1Exportt-1+α0EUPMIt+α1EUPMIt-1+η0USPMIt+η1USPMIt-1+λ0JPPMIt+λ1JPPMIt-1+μt

将历史数据带入上述公式，得到估计结果模型2为：

Exportt=0.793×Exportt-1+0.729×EUPMIt-0.468×EUPMIt-1-0.097×USPMIt+0.314×USPMIt-1+0.251×JPPMIt+0.191×JPPMIt-1-19.364

从模型的预测效果看，除了春节月份工业出口交货值变化较大之外，其他月份的预测效果较好。从图7可看出，预测走势与实际走势趋势基本吻合。模型1反映出，如果当期新出口订单指数上升1个百分点，会带动工业出口交货值增长0.53个百分点。从模型2中可以看到，如果当期欧元区PMI提高1个百分点，带动工业出口交货值上升0.73个百分点，提前1期的美国PMI提高1个百分点，带动我国工业出口交货值上升0.31个百分点，当期日本PMI上升1个百分点，向上拉动我国工业出口交货值0.25个百分点。

图7 模型1、2工业出口交货值预测值与实际值对比图

2. 我国新出口订单指数的预测

在向量自回归模型中通过脉冲响应分析和方差分解分析了新出口订单指数与各国PMI的关系，下面建立预测模型，将新出口订单指数作为外生变量，引入欧元区PMI、美国PMI、日本PMI作为内生变量，从滞后一阶开始拟合，最终确定的模型为：

CNEXt=β0+β1CNEXt-1+α0EUPMIt+α1EUPMIt-1+η0USPMIt+η1USPMIt-1+λ0JPPMIt+λ1JPPMIt-1+μt

将历史数据，带入上述公式，得到估计结果为：

CNEXt=0.635×CNEXt-1+0.693×EUPMIt-0.487×EUPMIt-1+0.155×USPMIt-0.072×USPMIt-1+0.204×JPPMIt-0.238×JPPMIt-1+10.600

从模型的预测效果看，各国PMI能较好地预测我国的新出口订单指数。从图8可看出，预测走势与实际新出口订单指数走势趋势基本吻合。模型反映出，如果当期欧元区PMI提高1个百分点，带动我国新出口订单指数上升0.69个百分点，当期的美国PMI提高1个百分点，带动我国新出口订单指数上升0.155个百分点，当期日本PMI上升1个百分点，向上拉动我国新出口订单指数0.20个百分点。

图8 新出口订单指数模型预测值与实际值对比图

四、主要结论

(一)欧、美、日PMI、我国新出口订单指数与我国工业出口的相关性较强

本文通过时差相关法分析表明，新出口订单指数与我国工业出口交货值相关性较强，且二者与欧元区PMI、美国PMI、日本PMI的走势基本一致。

(二)欧、美、日PMI和我国新出口订单指数均能有效预测我国工业出口趋势

通过时差相关法可以看出，欧元区PMI、美国PMI、日本PMI对我国工业出口交货值均有4-6个月左右的先行性；建立的ADL模型表明，我国新出口订单指数和欧、美、日PMI均能较好地预测我国工业出口趋势。

(三)欧、美、日PMI领先并可预测我国新出口订单指数的变动

通过建立VAR模型，揭示了各国PMI与我国新出口订单指数的内部关系。从格兰杰因果检验中可以看到，各国PMI的变动是影响我国新出口订单指数的格兰杰原因，因此，能够通过各国PMI的变动来预测我国新出口订单指数。从脉冲响应和方差分解分析中可以看出，欧元区PMI对我国新出口订单指数的脉冲扰动和方差贡献度均为三个PMI中的最高值，美国和日本PMI大致相当，且明显低于欧元区PMI。从建立的ADL模型中可以看到，欧、美、日PMI对我国新出口订单指数的变动具有较好的预测性。

总之，有效利用国外PMI和我国新出口订单指数，能够一定程度上预测我国的工业出口趋势，为政府部门制定相关政策提供有力的理论支持，同时有助于外贸出口企业对市场发展趋势进行预测，通过外部市场的变动情况制定符合企业长期发展要求的战略，并合理调整企业用于出口的生产计划。

[1]杨兴武.中国采购经理指数(PMI)对GDP影响的传导路径分析[J].统计与决策,2016(5).

[2] 陈晴旖.基于PMI指数对我国经济增长进行预测的实证研究[J].统计研究,2013(4).

[3] 张利斌，冯益，刘龙飞，张竹.制造业PMI 对GDP 走势的预测作用[J].中南民族大学学报，2012(9).

[4] 易丹辉.数据分析与EVIEWS应用[M].北京:中国人民大学出版社,2008.

(责任编辑：孙建华)

Empirical Analysis on New Export Order Index of PMI

LI Na

(Department of Service Statistics, National Bureau of Statistics, Beijing 100826, China)

In recent years, with the increasing value of international trade, China has gradually integrated into globalization. China's manufacturing exports are affected by fluctuation of major trade partners. This paper makes an empirical analysis on New Export Order Index of manufacturing PMI, in order to play the role of forecasting economics. This paper makes time-difference correlation analysis and VAR model with data of manufacturing New Export Order Index, European PMI, USA PMI, Japanese PMI and China's export value of industrial enterprises, and it predicts future values of exports and New Export Order Index.

PMI; New Export Order Index; value of exports; VAR model

2017-02-24

李娜(1982- ),女,山东栖霞人,中级统计师,经济学硕士，研究方向为采购经理指数，经济预测。

F746.12

A

1671-4385(2017)03-0004-07