列车橡胶弹簧参数识别方法研究

杨 恒， 伍川辉， 李艳萍， 胡永旭， 吴 琛

(1. 西南交通大学 机械工程学院， 四川 成都 610031；2. 西南交通大学 牵引动力国家重点实验室， 四川 成都 610031)

列车橡胶弹簧参数识别方法研究

杨 恒1， 伍川辉1， 李艳萍1， 胡永旭2， 吴 琛1

(1. 西南交通大学 机械工程学院， 四川 成都 610031；2. 西南交通大学 牵引动力国家重点实验室， 四川 成都 610031)

针对难以准确判断高速列车车下悬挂装置内橡胶弹簧是否失效的问题， 提出了通过广义卡尔曼参数识别算法对装置的阻尼及刚度进行识别从而判断橡胶弹簧工作状态的诊断方法. 针对卡尔曼滤波器跟踪速度不足的问题， 应用自适应-强跟踪卡尔曼滤波算法对卡尔曼算法进行改进， 提高辨识速度. 通过对仿真信号及实测数据的辨识结果对滤波器性能进行了验证， 结果表明自适应-强跟踪滤波器能够快速对参数进行跟踪.

橡胶弹簧状态监测； 自适应-强跟踪卡尔曼滤波器； 参数识别； 列车悬挂装置

目前， 国内高速客车大量采用设备车下悬挂的设计方式. 从现有资料来看， 为了降低车下设备对车体振动的影响， 目前国内CRH1， CRH2， CHR3， CRH5等很多车下设备均采用弹性减振系统. 由于在不同频率的振动加载下， 橡胶的阻尼比呈现为非线性变化， 对高频振动的减振能力很强， 所以目前橡胶广泛应用于高速列车弹性悬挂减振装置中. 但是橡胶件在长期受氧化和受热后会出现硬化、 软化、 发粘和粉化等故障[1]， 在寿命的末期可能出现局部断裂， 系统的阻尼和刚度参数也会出现剧烈波动， 对高速列车的运行舒适性及安全性带来很大影响. 由于仅仅通过监测悬挂系统的振动加速度不能准确反应橡胶弹簧的工作状态， 故需要提出更能反应橡胶弹簧工作情况的参数计算方法.

基于上述原因， 有必要对列车悬挂装置的机械参数进行识别， 以便在橡胶失效后进行更换. 目前的参数识别算法有最小二乘法、 递推最小二乘法、 广义卡尔曼辨识算法、 边缘粒子滤波法等. 文献[2]提出了结合边缘粒子滤波与广义卡尔曼参数识别相结合的参数识别算法， 需要结合数据的统计特性. 文献[3]提出了通过自适应计算遗忘因子从而改进递推最小二乘法的变遗忘因子RLS算法， 使RLS算法的跟踪能力和稳定性得到加强. 文献[4]通过递推最小二乘法对橡胶弹簧的Bouc-Wen模型进行了实验条件下的参数识别， 但是需要先在静态载荷条件下识别弹簧的刚度参数. 文献[5]通过广义卡尔曼算法实现了在动态试验条件下对橡胶弹簧的Bouc-Wen模型的参数识别， 具有较好的效果.

本文论述了广义卡尔曼滤波器的理论算法和卡尔曼算法在状态增广后非线性化状态方程转化为线性方程的一般方法， 之后对弹簧阻尼系统的Klevin-voight模型进行了离散化[6,7]， 推导出了模型的离散化状态空间方程； 针对离散化状态空间模型预测误差参数驱动能力弱的问题提出了广义卡尔曼算法的改进算法： 自适应-强跟踪算法， 并用仿真和实测信号的参数识别效果验证算法的有效性.

1 广义卡尔曼算法概述

考虑如下离散系统， 方程(1)表示系统的状态方程， 方程(2)表示系统的观测方程.

(1)

(2)

首先考虑f(·)为线性方程， 将状态向量增广后， 状态一步跟新方程为

(3)

(4)

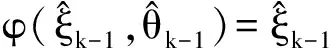
(5)

(6)

由于卡尔曼滤波器是用预测误差来修正原来的状态估计， 故

(7)

(8)

(9)

所以误差协方差矩阵更新算法为

(10)

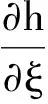
(11)

(12)

若f(x)为非线性函数， 则将f(x)用泰勒级数展开并忽略2阶及以上项将f(x)化为线性函数， 此时得到的滤波值为近似值， 误差增大.

根据以上的式(3)， (6)， (7)， (10)， (12)可以完成系统的参数识别.

2 模型离散化状态空间方程

Klevin-voight模型将弹簧阻尼系统简化为弹簧与阻尼器并联的结构， 如图 1 所示.

图 1 Klevin-voight弹簧阻尼模型Fig.1 Klevin-voight model

其微分方程表达式为

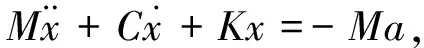
(13)

式中： x表示系统相对位移； a表示系统输入加速度信号； M表示系统质量； C表示系统阻尼； K表示刚度[9].

系统的0初始状态x(0)和x′(0)为0， 则系统的拉式变换为

(14)

(15)

式(15)对应的离散化状态空间方程为

(16)

(17)

式中：

(18)

(19)

3 自适应-强跟踪滤波算法

3.1 自适应-强跟滤波算法推导

考虑将状态估计误差验前协方差阵乘以加权系数λk+1， 其算法

(20)

加权系数λk+1的计算方法为

(21)

式中： B表征系统的增益， 可以用输入输出的有效值之比来衡量， 其计算方法为

(22)

在实际识别过程中， 先要对信号进行有限长度截取， 保证截取范围内的输入输出信号有效值之比基本固定， 再使用被测信号进行参数识别.

3.2 算法验证

以一时变离散模型为例， 其表达式为：

(23)

式中： N为输入信号长度，ΔT为系统采样时间间隔， 当ΔT较小时， 系统输出很小. 输入信号为正余弦叠加信号并叠加一定强度的白噪声， 输入输出信号如图 2 所示.

分别使用广义卡尔曼滤波算法和自适应-强跟踪滤波算法对仿真信号进行参数识别， 其结果如图 3 所示.

图 2 仿真输入输出信号Fig.2 The simulation input/output signals

图 3 滤波器识别效果对比Fig.3 Comparison of Effect of different filters

加权系数在辨识过程中的计算值如图 4 所示.

图 4 加权系数计算值Fig.4 Calculation of weighting coefficient

图 3 表明运用卡尔曼滤波算法将参数初值迭代到实际稳定值经过约3 000个时间点， 自适应-强跟踪滤波算法只经过了约100个时间点； 当系统参数在第5 000个点出现突变时， 广义卡尔曼算法使参数重新稳定的过程约为300个点， 自适应-强跟踪滤波算法只经过了约50个点. 仿真信号的辨识结果表明自适应-强跟踪滤波算法的识别速度要优于广义卡尔曼滤波算法.

图 4 表明在辨识初始过程和参数突变时刻， 加权系数会增大以使得状态变量能够快速从初值迭代至实际值； 其他时刻加权系数保持在略大于1以保证预测误差的参数驱动能力.

4 实测数据识别结果

根据式(3)， 可推导Klevin-voight模型状态转移方程为

(24)

观测方程为

(25)

式中：

(26)

状态转移矩阵的雅克比矩阵为

(27)

(28)

(29)

式中：ΔT为采样时间间隔； C为待辨识的阻尼参数； K为待辨识的的刚度参数； M为系统质量， 为已知量.

对一定速度下车体垂向振动加速度及牵引变压器—车体下底板垂向位移变化量进行测量， 共有4组测点， 分别在牵引变压器四角对应位置. 加速度测点位于列车车体下底板， 如图5(a)所示； 位移测点位于牵引变压器侧板， 如图5(b)所示.

图 5 加速度测点(上)、 位移测点(下)示意图Fig.5 The acceleration point(above) and the displacement measuring point(below)

从实测数据中截取5s数据， 如图 6 所示.

图 6 实测信号曲线Fig.6 The measured signal curve

图 7 卡尔曼算法识别结果Fig.7 Identify results of Kalman filter

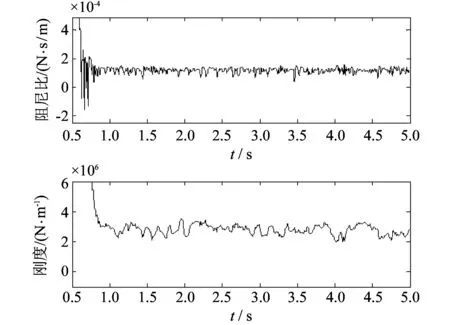
图 8 自适应-强跟踪算法识别结果Fig.8 Identify results of adaptive-strong tracking filter

分别使用卡尔曼滤波器和强跟踪-自适应卡尔曼滤波器进行参数识别， 识别结果如图 7 和图 8 所示.

根据供货厂家提供的列车悬挂弹簧技术资料， 其刚度为2.67×106N/m，阻尼为1.34×104N·s/m. 图 7 表明广义卡尔曼滤波算法的阻尼参数辨识结果在5s内未达到稳定值； 图8表明在该初值下， 自适应-强跟踪算法的辨识结果在1s内稳定， 且辨识结果在参考值的附近波动.

下面对列车在某段区间内匀速运行时所记录的加速度、 相对位移数据进行参数识别. 由于在采样时间内采样点十分丰富， 如果对每个采样点的辨识结果都进行储存十分耗费时间， 故选择对每秒的辨识结果求取平均值再进行存储， 4个测点的辨识结果如图 9 所示.

图 9 测点1—4参数辨识结果Fig.9 Identify results of measuring point 1—4

从实测数据的辨识结果来看， 基本可以得出以下结论：

1) 由于输入信号不稳定， 辨识结果在试验条件下的测算结果附近波动.

2) 一些区间内参数值出现较大波动和负值， 表明当输入数据受到较大干扰后， 辨识结果会出现失真.

5 结 论

通过对弹簧阻尼系统的Klevin-voight模型进行离散化， 获得了系统的离散状态空间模型. 增维后， 离散线性模型成为非线性模型， 通过泰勒展开将非线性模型线性化后可以通过卡尔曼滤波器进行参数求解. 通过强跟踪—自适应滤波器可以增强卡尔曼滤波器在系统参数突变时的跟踪能力， 又可以在参数稳定时增强预测误差的参数驱动能力， 适合在模型不完全精确， 参数模型波动频繁的情况下对系统参数进行识别. 通过对高速列车弹性悬挂系统的实测数据参数识别， 证明该方法能快速识别系统参数,辨识结果符合橡胶弹簧的理论特性.

[1] 候学勤， 范金娟. 橡胶密封件的失效分析与橡胶断口形态[J]. 世界橡胶工业， 2010， 37(12)： 33-37.HouXueqin,FanJinjuan.Failureanalysisandfracturemorphologyofrubberofrubberseals[J].WorldRubberIndustry, 2010, 37(12)： 33-37. (inChinese)

[2] 丁建明. 车辆动力学性能参数估计方法研究[D]. 四川成都： 西南交通大学， 2007.

[3] 李倩茹， 王于丁， 张晓芳. 一种变遗忘因子RLS算法的分析与仿真[J]. 现代电子技术， 2008(17)： 45-47.LiQianri,WangYu-ding,ZhangXiao-fang.AnalysisandsimulationofvariableforgettingfactorRLSalgorithm[J].ModernElectronicsTechnique, 2008(17)： 45-47. (inChinese)

[4] 朱旭东， 吕西林， 徐崇恩. 软钢阻尼器基于Bouc-Wen模型的参数识别研究[J]. 结构工程师， 2011, 27(5)： 124-128.ZhuXudong,LüXilin,XuCongen.Parametricidentificationofmildsteeldamperbasedondddbouc-wenmodel[J].StructuralEngineers, 2011, 27(5)： 124-128. (inChinese)

[5] 尹强， 周丽. 基于EKF方法的橡胶隔震支座参数识别实验研究[J]. 南京航空航天大学学报， 2012， 44(1)： 43-49.YinQiang,ZhouLi.Experimentalstudyonparameteridentificationofnon-linerhystereticrubber-bearingisolatorsusingEKFmethod[J].JournalofNanjingUniversityofAeronautics&Astronautics， 2012， 44(1)： 43-49. (inChinese)

[6] 刘军. 随机连续系统离散化方法和分析[J]. 系统工程与电子技术， 1995(11)： 74-80.LiuJun.AnalysisandMethodsaboutthediscretizationofrandomcontinuousystems[J].SystemsEngineeringandElectronics, 1995(11)： 74-80. (inChinese)

[7] 张力军， 钱山， 蔡洪， 等.Kalman滤波中连续系统离散化的计算机实现[J]. 飞行器测控学报， 2010， 29(2)： 66-69.ZhangLijun,QianShan,CaiHong,etal.ComputerimplementationtodiscretizationofcontinuoussystemforKalmanfilter[J].JournalofSpacecraftTT&CTechnology, 2010， 29(2)： 66-69. (inChinese)

[8]ParkS,LeeJG.Designofapracticaltrackingalgorithmwithradarmeasurements[J]IEEETransonAerospaceandElcetronicSystems, 1998, 34(4)： 1337-1344.

[9] 白艳艳， 张小俊. 建立弹簧-质量-阻尼系统数学模型的数轴法[J]. 噪声与振动控制， 2011(3)： 59-62.BaiYanyan,ZhangXiaoJun.Numercial-axismethodforestablishingthemathenaticalmodelofmass-spring-dampersystem[J].NoiseandVibrationControl, 2011(3)： 59-62. (inChinese)

[10] 李益化.MATLAB辅助现代工程数字信号处理[M]. 西安： 西安电子科技大学出版社， 2010.

[11] 付梦印， 邓志红， 张继伟.Kalman滤波理论及其在导航系统中的应用[M]. 北京： 科学出版社， 2003.

[12] 范文兵， 刘春风， 张素贞. 一种强跟踪扩展卡尔曼滤波器的改进算法[J]. 控制与决策， 2006， 21(1)： 73-76.FanWenbing,LiuChunfeng,ZhangSuzhen.ImprocedmethodofstrongtrackingextendedKalmanfilter[J].ControlandDecision, 2006, 21(1)： 73-76. (inChinese)

Research About Identification Method of Rubber Damp In Railway

YANG Heng1, WU Chuanhui1, LI Yanping1, HU Yongxu2, WU Chen1

(1. Southwest Jiao-tong University, School of Mechanical Engineering, Chengdu 610031, China；2. Southwest Jiao-tong University, Traction Power Laboratory, Chengdu 610031, China)

For estimating invalidation of the rubber damp which equipped in suspension device of high speed railway, Extended Kalman Filter was put forward to recognize the damp and stiffness of the device to judge whether the rubber damp was working regularly. Self Adaption-Strong Tracking Kalman Filter which is a improvement of Extended Kalman Filter was put forward to solve the problem of slow tracking speed. In this way, recognition speed was advanced. Through the recognize of simulate signal and test data, the filter performance was verified. The results indicate Self Adaption-Strong Tracking Klman Filter is efficacious to track the fluctuation of suspension parameter.

Rubber spring condition monitoring; self adaption-strong tracking kalman filter; parameter identification; suspension device of the train

1671-7449(2017)03-0215-08

2016-12-17

国家自然科学基金资助项目(61134002)

杨 恒(1991-)， 男， 硕士生， 主要从事智能状态监测及故障诊断等研究.

U270.16

A

10.3969/j.issn.1671-7449.2017.03.006