单通道信源数估计的改进方法

董 志， 胡君朋， 黄芝平

(国防科技大学 机电工程与自动化学院， 湖南 长沙 410073)

单通道信源数估计的改进方法

董 志， 胡君朋， 黄芝平

(国防科技大学 机电工程与自动化学院， 湖南 长沙 410073)

本文对单通道接收信号的源数估计方法进行了研究， 提出了对现有方法的改进措施. 将单通道数据通过延迟处理转换为多通道形式， 然后引入阵列信号处理中的信源数估计算法， 如盖氏圆盘估计法(Gerschgorin’s Disk Estimation, GDE)和最小描述字长法(Minimum Dscription Lengh, MDL). 基于信息理论标准(ITC)的MDL方法在低SNR条件下获得比GDE更好的性能， 但是它无法处理包含有色噪声的信号. GDE方法虽然可以克服有色噪声的影响， 但是其在低SNR下的性能欠佳. 基于上述考虑， 本文对这两种方法进行了改进. 采用对角加载技术改善MDL方法的性能， 并引入Jackknife切法优化数据协方差矩阵， 以提高GDE方法的性能. 模拟实验结果表明： 本文提出的方法使原有方法的性能得到很大改善.

单通道信号； 信源数估计； 自助刀切； 信息论准则； 盖氏圆； 最小描述字长(MDL)

0 引 言

单信道源数估计(SCSNE)的问题被广泛应用于许多领域， 例如图像处理， 光纤通信[1-3]和单信道盲信号分离(SCBSS)等. 近年来， SCBSS被认为是一些领域中最具挑战性的研究课题之一[4-7]. 相关学者提出了许多算法来解决SCBSS问题， 例如MUSIC[8]， ESPRIT[9]和ICA[10]. 然而， 大多数盲源分离(BSS)算法和信号谱估计方法的性能将随着源数目的不准确估计而显著恶化.

对于单通道信号的处理， 一种可接受的方式是扩展数据维数并将单通道数据转换为多通道形式. 目前， 有多种方法来扩展数据维度， 如过采样方法[11]， 信号稀疏分解[12]和延迟处理[13]. 其中， 过采样方法需要数据采样前端的协作； 稀疏分解方法计算复杂度较高， 并且不是所有信号都具有稀疏特性； 延迟过程相对简单， 复杂度低， 但它需要较大数据量.

在文献中已经出现了许多优秀的信源数估计算法， 例如基于假设检验方法[14,15]， 基于信息理论准则(ITC)的方法[16]和盖氏圆估计(GDE)方法[17]. 基于假设检验的方法需要设置人工阈值， 这在一些条件下不是容易的决定. 基于ITC的方法， 主要由Akaike信息标准(AIC)[16]和最小描述字长(MDL)[18]表示， 建立在信号和噪声的特征值之间的差异， 计算复杂度相对较低， 但是它们不能用于有色噪声. GDE方法可以处理有色噪声， 但其性能在低SNR条件下恶化.

本文详细介绍了MDL和GDE方法估计单通道接收信号源数量的方法. 单通道数据通过延迟处理变换为多通道形式. 模拟结果表明， 当接收信号包含有色噪声时， MDL方法不能有效地估计源数. GDE方法在低SNR下的性能较差， 尽管它可以使用有色噪声进行管理. 为了提高这些方法的检测性能， 引入了用于MDL方法的对角加载技术， 并且使用自助刀切技术来优化GDE的数据协方差矩阵. 仿真结果表明， 本文提出的方法可以有效地获得单通道接收信号的源数， 本文提出的改进取得了显著进步.

1 信号模型

多通道接收信号模型可描述如下[29-32]

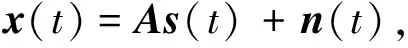
(1)

在单通道条件下， 在每个时间点只能观察到一个数据. 信号模型变为

(2)

式中： X(t)=[x(1),x(2),…,x(m)]表示观测数据； t表示观测时间； A=[a1,a2,…,am]是混合矩阵； S(t)=[s1(t),s2(t),…,sm(t)]T是源信号矩阵； 噪声和信号是独立的， 单信道信号的参数估计是一个欠定的问题.

2 多信道的构建

单通道接收数据是一维矩阵. 为了利用多通道信源数据估计算法， 必须扩展数据矩阵的维度. 本文使用延迟处理从单通道接收数据构造多通道数据矩阵. 假设单通道数据表示为y(n), n-1,2,…,L， 接收信号可以用延迟处理表示为

(3)

因此， 形成了N通道接收数据.

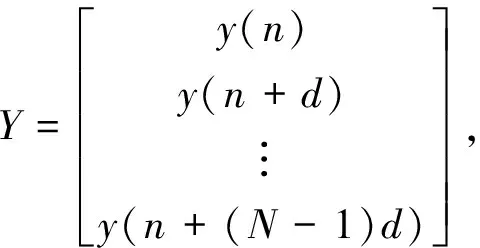
(4)

式中： d描述了每个通道的延迟长度. N是通道的总数， 不应小于信源的数量.

每个构造的信道的数据应当通过旨在对接收信道具有更现实响应的滤波器. 将每个滤波器的频率响应设置为

(5)

式中： |H0(ejω0)|表示原型FIR滤波器的振幅频率响应. φi(ω)表示每个通道的相位频率响应. 因此， 最终的多通道数据矩阵可以表示为

(6)

式中： hi, i=1,2,…,l是每个通道的滤波器的脉冲响应函数. 通过上述过程， 具有1×L接收数据的单信道接收信号被变换为具有N×(d+l-1)维度的多信道信号.

3 信源数估计算法

3.1MDL方法

假设噪声和源信号相互独立且无关. 则可以重写观测信号的协方差矩阵为

(7)

式中： RS=E{S(t)ST(t)}是信号协方差矩阵； σ2I表示噪声的协方差矩阵； RX通过特征值分解(EVD)进行变换以获得其特征值

(8)

λi, i=1,…,p是特征值， ui, i=1,…,p是对应的特征向量.

由于噪声和信号是独立的， RX的特征值可以被分解为λ1=μ1+σ2,λ2=μ2+σ2,…,λn=μn+σ2,λn+1=λn+2=…=λm=σ2. 理想情况下， 信号的特征值远大于噪声的特征值. 源号等于大于预设阈值的特征值的量.

然而， 由于快照的数量有限和多径传播的影响， 噪声和信号的特征值是混杂的. 需要引入一些标准来精确估计源的数量.MDL用于基于最短码长度的概念来选择模型， 由Rissanen提出[18,31].MDL的估计函数可以表示为.

(9)

(10)

其中

(11)

并且可以通过最小化MDL的函数来产生源的数量

(12)

MDL的方法通过信号和噪声之间的特征值的差来估计源数. 它的计算复杂度相对较低， 但它不能处理带有色噪声的信号.

本文引入克服有色噪声影响的对角加载技术[33-35]

(13)

式中： λi, i=1,2,…,p是RX的原始特征值； λDL是负载值； βi是具有对角荷载的最终特征值.

对角加载过程对较大的特征值产生很小的影响， 并且对应于噪声的较小特征值将收敛到接近负载值. 因此， 通过对角加载过程， 噪声特征值近似相等， 并且该过程的效果等同于使有色噪声白化.

负载值λDL的选择对这种方法有很大的影响. 小的λDL值对估计几乎没有改进， λDL过大可能破坏噪声和信号之间的特征值的差异.

因此， 负载值λDL应满足

(14)

式中： λN表示噪声特征值， λN表示信号特征值. 为了满足这个条件， 一个可行的λDL表示为[33]

(15)

然后， RX的特征值被转换为对角负载

(16)

3.2GDE方法

对于p×p矩阵， rij是行i和列j的元素. 除了该i元素之外的i行中的其它元素的总和被定义为

(17)

圆盘ith表示复平面中心rij和半径Ci的圆.

(18)

Gerschgorin已经证明矩阵的特征值包括在磁盘Oi, i=1,…,p的区域中. 使得R的特征值满足以下不等式中的至少一个

(19)

信号协方差矩阵由EVD表示，

(20)

式中： U是由协方差矩阵R的特征向量构成的p阶酉矩阵. U=[u1,u2,…,up]， UUH=I. Λ是p阶对角矩阵， 其对角元素是矩阵R的特征值, Λ=diag[λ1,…,λp]. R可以以块矩阵的形式重写为

(21)

式中： R1是通过删除R的最后一行和列而获得的p-1阶次序子矩阵； r是由R的p列中的前面p-1元素构成的列向量， 即r=[r1p,…,r(p-1)p]T， R1可以通过EVD转化为

(22)

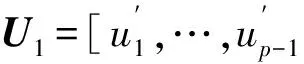
(23)

然后构造一个p阶矩阵Ud.

(24)

(25)

用Ud变换协方差矩阵R.

依据上面的方程， 矩阵S的前ρ-1Gerschgorin的圆盘半径可以写为

(26)

矩阵的噪声特征向量与列向量正交， 但是信号特征向量不是正交的， 而是满秩矩阵， 因此， 可以进一步简化协方差矩阵.

(27)

Gerschgorin磁盘S分为两组. 具有非零半径和较大中心点的属于实际信号， 而其它的对应于噪声. 因此，S中的非零Gerschgorin磁盘半径数量等于估计的源数量. 在实际应用中， 由于快照的数量有限， 将存在一些偏差， 并且噪声的盘半径不总是为零， 于是介绍了GDE方法来确定源的数量

(28)

式中：D(N)是值在0和1之间的调整因子.

计算式(27)从k=1到k=p， 当第一次取负值时， 计算将停止， 估计的数量为k=1.

GDE方法通过利用变换的协方差矩阵半径的大小来获得源数. 与基于ITC的方法相比， 它具有在有色噪声的条件下保持良好行为的优点.

然而， GDE方法受到其在低SNR下性能差的限制， 采用Jackknife切法技术优化数据协方差矩阵， 可以降低噪声的影响， 以提高GDE在低SNR下的性能.

Jackknife是统计领域中使用的有效策略. 它可以充分利用接收的数据实现更准确的检测和估计[19]. 对于Jackknife， 通过每次删除一部分数据来重构数据结构， 并且它可以减少估计器的偏差.

通过延迟处理从单通道数据获得了数据矩阵

(29)

Y被视为具有N元素的集合. 随机地从Y中选择M个元素以形成子集

(30)

(31)

重复上述处理时间K次， 获得一系列协方差矩阵Rj, j=1,2,…,K. 计算这些矩阵的平均值

(32)

4 实 验

本节通过仿真实验结果来证明上述每种信源数估计方法的性能.

4.1 比较接收信号包含白高斯噪声时MDL和GDE的估计性能

图 1 具有白噪声的MDL和GDE的检测概率Fig.1 Detection probability of MDL and GDE with white noise

假设单通道接收信号出现在3个独立的源信号， 其在Matlab环境中构建. 观测数据长度设置为L=5 000， 延迟为d=600. 通过延迟过程， 虚拟通道的数量M=8. 因此， 单通道数据被扩展为8×600的数据矩阵. 接收信号的SNR从-20dB增加到20dB. 每个条件的实验重复500次. 第一个实验结果如图 1 所示.

从图 1 可以推断，MDL和GDE方法都利用白高斯噪声实现了良好的估计性能. 然而， 由于Gerschgorin磁盘半径受噪声影响相对容易，GDE方法的性能略低于MDL在低SNR的性能.

4.2 将MDL和GDE的估计性能与有色噪声进行比较

本实验的条件与第一个相同， 只是白噪声被有色噪声替代. 通过500次蒙特卡罗实验， 结果如图 2 所示. 结果表明：MDL的方法已经失去了有色噪声的估计能力， 但GDE方法仍然可以保持良好的性能.

4.3 比较MDL， 改进的MDL，GDE和改进的GDE与有色噪声的估计性能

实验条件设置为与第一和第二实验条件相同. 图 3 显示了这些方法在不同SNR下的检测概率.

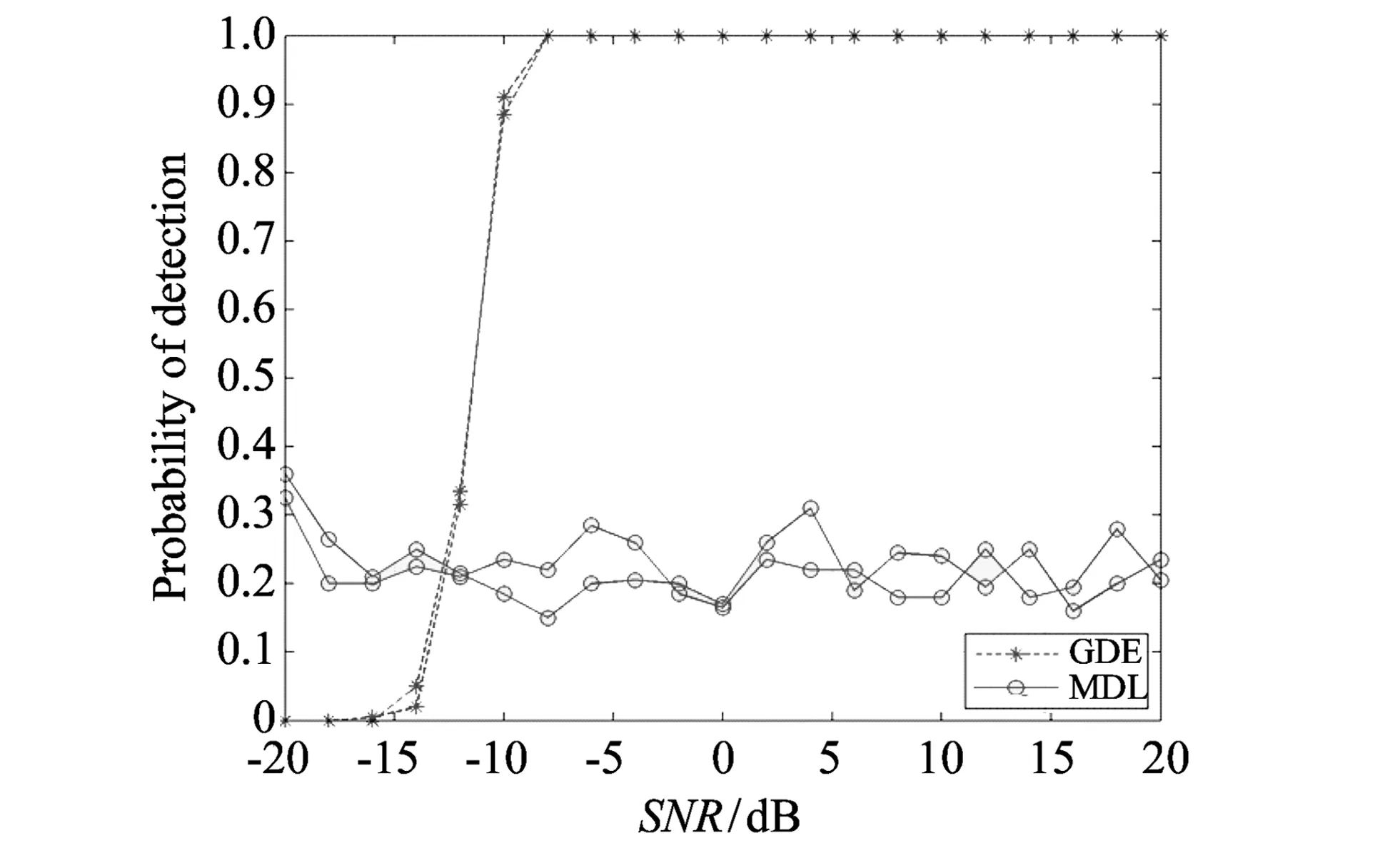
图 2 带有彩色噪声的MDL和GDE的检测概率Fig.2 Detection probability of MDL and GDE with colored noise

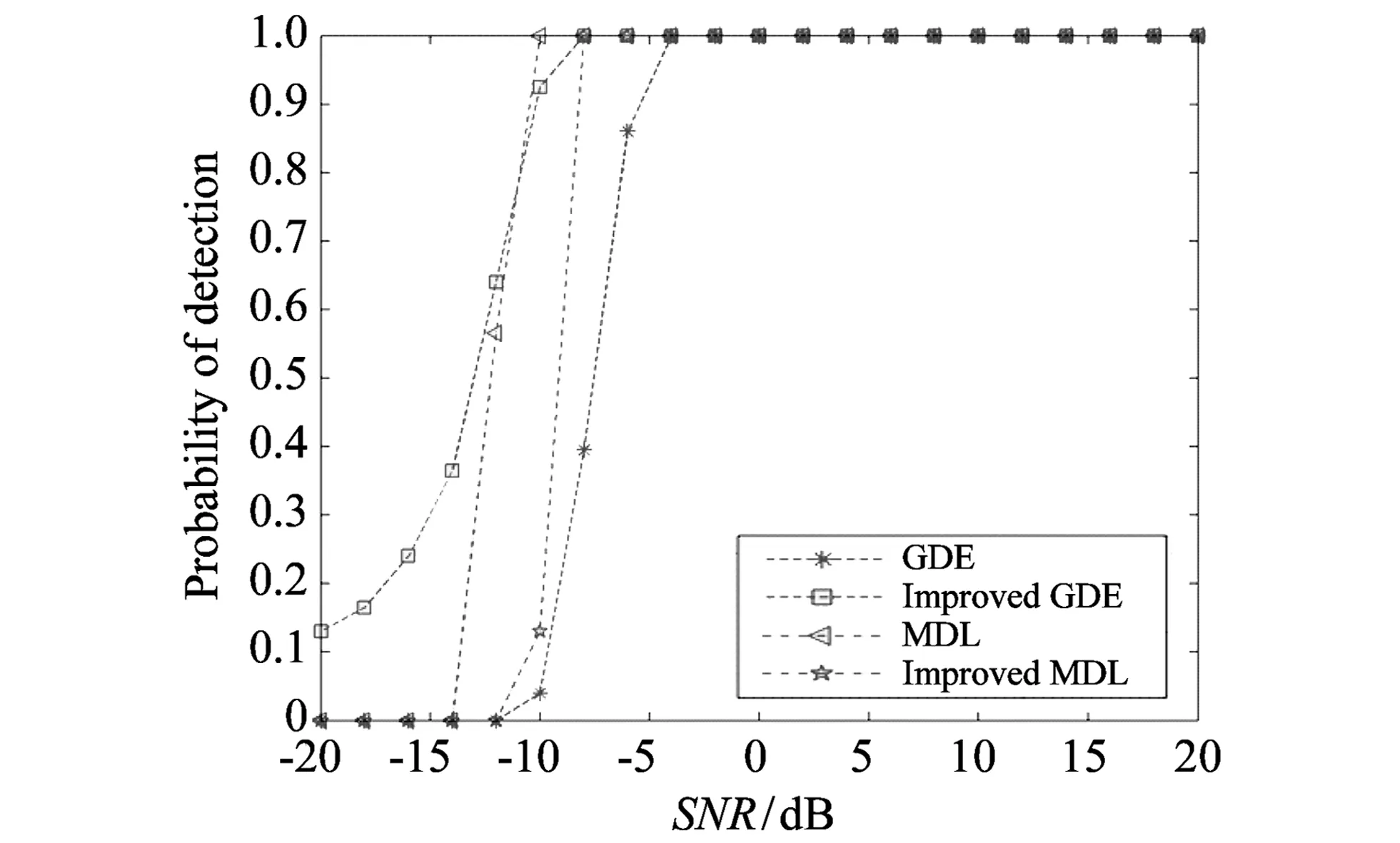
图 3 具有白噪声的原始和改进方法的检测概率Fig.3 Detection probability of original and improved methods with white noise

由图 3 可以得出结论：boosting使得MDL和GDE方法的性能有很大提高； 改进的MDL方法可以消除有色噪声的影响， 使GDE方法在低SNR下保持更好的性能.

5 结 论

使用单通道接收数据估计信源数是一个具有普遍性和挑战性的问题. 本文研究了MDL和GDE方法用于解决信源数估计问题. 为了有效利用阵列信号处理中的现有算法， 通过延迟处理将单通道接收数据转换为多维形式，并构造数据协方差矩阵.本文引入对角加载技术来优化MDL方法，使其能够克服有色噪声的影响.同时，采用自助刀切技术来提高GDE方法在低SNR条件下的性能. 实验结果证明： 本文所做的改进使得MDL方法可以克服有色噪声的影响， 改进后的GDE方法获得比原始方法更好的性能.

[1]SongH,Brandt-PearceM.A2-ddiscrete-timemodelofphysicalimpairmentsinwavelength-divisionmultiplexingsystems[J].JournalofLightwaveTechnology, 2012, 30(5)： 713-726.

[2]SongH,Brandt-PearceM.Rangeofinuenceandimpactofphysicalimpairmentsinlong-hauldwdmsystems[J].JournalofLightwaveTechnology, 2013， 31(6)： 846-854.

[3]SongH,Brandt-PearceM,editors.Model-centricnonlinearequalizerforcoherentlong-haulfiber-opticcommunicationsystems[C].ProceedingsofIEEEGlobalCommunicationsConference(GLOBECOM)， 2013，Atlanta,GA.

[4]ChengW,ZhangZS,CaoHR,etal.Acomparativestudyofinformation-basedsourcenumberestimationmethodsandexperimentalvalidationsonmechanicalsystems[J].Sensors, 2014， 14(5)： 7625-7646.

[5]GaoB,WooWL,DlaySS.Unsupervisedsingle-channelseparationofnonstationarysignalsusinggammatonefilterbankanditakura-saitononnegativematrixtwo-dimensionalfactorizations[J].IEEETransactionsonCircuitsandSystems, 2013， 60(3)： 662-675.

[6]ReddyAM,RajB.Softmaskmethodsforsingle-channelspeakerseparation[J].IEEETransactionsonAudio,Speech,andLanguageProcessing, 2007， 15(6)： 1766-1776.

[7]KingBJ,AtlasL.Single-channelsourceseparationusingcomplexmatrixfactorization[J].IEEETransactionsonAudio,Speech,andLanguageProcessing,, 2011， 19(8)： 2591-2597.

[8]SchmidtR.Multipleemitterlocationandsignalparameterestimation[J].IEEETransAntennasPropag, 1986， 34(3)： 276-280.

[9]RoyR,KailathT.Esprit-estimationofsignalparametersviarotationalinvariancetechniques[J].IEEETransAcoustSpeechSignalProcess, 1989， 37(7)： 984-995.

[10]DaviesME,JamesCJ.Sourceseparationusingsinglechannelica[J].SignalProcessing, 2007, 87: 1819-1832.

[11]WarnerES,ProudlerIK.Single-channelblindsignalseparationoffilteredmpsksignals[J].IEEProceedingsofRadar,Sonar&Navigation, 2003， 150(6)： 396-402.

[12]SZUH,ChanyagornP,KoprivaI.Sparsecodingblindsourceseparationthroughpowerline[J].Neurocomputing, 2002， 48(1)： 1015-1020.

[13]JamesCJ,LoweD,editors.Singlechannelanalysisofelectromagneticbrainsignalsthroughicainadynamicalsystemsframework[C].EMBS, 2001，Istanbul,Turkey, 2011: 1974-1977.

[14]BrcichRF,ZoubirAM,PelinP.Detectionofsourcesusingbootstraptechniques[J].IEEETransSignalProcess, 2002， 50(2)： 20-215.

[15]XiaoM,WeiP,TaiH-M.Estimationofthenumberofsourcesbasedonhypothesistesting[J].JournalofCommunicationsandNetworks, 2012， 14(5): 481-486.

[16]AkaikeH.Anewlookatthestatisticalmodelidentification[J].IEEETransonAutomaticControl, 1974， 19(6)： 716-723.

[17]WuHT,YangJF,ChenFK.Sourcenumberestimatorusinggerschgorindisks[J].IEEETransonAcousticsSpeechSignalProcessing, 1994， 4(4)： 261-264.

[18]RissanenJ.Modelingbyshortestdatadescription[J].Automatica, 1978， 14： 465-471.

[19]HanKY,NehoraiA.Improvedsourcenumberdetectionanddirectionestimationwithnestedarraysandulasusingjackknifing[J].IEEETransactionsonSignalProcessing, 2013， 61(23)： 6118-6128.

[20]Román-MontoyaY,RuedaM,ArcosA.Condenceintervalsforquantileestimationusingjackknifetechniques[J].ComputStat, 2008， 23： 573-585.

[21]JimingJiangBY,LahiriP,WanSM.Aunifiedjackknifetheoryforempiricalbestpredictionwithm-estimation[J].TheAnnalsofStatistics, 2002， 30(6)： 1782-1810.

[22]ChambersMJ,KyriacouM.Jackknifeestimationwithaunitroot[J].StatisticsandProbabilityLetters, 2013， 83： 1677-1682.

[23]ChambersMJ.Jackknifeestimationofstationaryautoregressivemodels[J].JournalofEconometrics, 2013， 172： 142-157.

[24]GuJF,WeiP,TaiHM.Detectionofthenumberofsourcesatlowsignal-to-noiseratio[J].IETSignalProcess, 2007， 1(1)： 2-8.

[25]BarbedoJGA,LopesA,WolfePJ.Empiricalmethodstodeterminethenumberofsourcesinsingle-channelmusicalsignals[J].IEEETransactionsonAudio,Speech,andLanguageProcessing, 2009， 17(7)： 1435-1444.

[26]HuangL,LongT,MaoE,SoHC.Mmse-basedmdlmethodforaccuratesourcenumberestimation[J].IEEESignalProcessingLetters, 2009， 16(9)： 798-801.

[27]XiaoML,WeiP,TaiHM.Estimationofthenumberofsourcesbasedonhypothesistesting[J].JournalofCommunicationsandNetworks, 2012， 14(5)： 481-486.

[28]HuangL,LongT,MaoE,etal.Mmse-basedmdlmethodforrobustestimationofnumberofsourceswithouteigendecomposition[J].IEEETransactionsonSignalProcessing, 2009， 57(10)： 4135-4142.

[29]ShojafarM,AbolfazliS,MostafaeiH,etal.Improvingchannelassignmentinmulti-radiowirelessmeshnetworkswithlearningautomata[J].WirelessPersonalCommunications, 2015， 82(1)： 61-80.

[30]ShojafarM,CordeschiN,BaccarelliE.Energy-efcientadaptiveresourcemanagementforreal-timevehicularcloudservices[J].IEEEtransactionsonCloudComputing, 2016, 2(3): 1-14.

[31]ChengW,LeeS,ZhangZS,etal.Independentcomponentanalysisbasedsourcenumberestimationanditscomparisonformechanicalsystems[J].JournalofSoundandVibration, 2012， 331(23)： 5153-5167.

[32]WaxM,KailathT.Detectionofsignalsbyinformationcriteria[J].IEEETRANSAcoustic,Speech,andSignalProcess, 1985，ASSP-33(April)： 387-392.

[33]JilingX,XicaiS.Determingthenumberofsourcesbasedondiagonalloadingtothecovariancematrix[J].SystemsEngineeringandElectronics, 2008， 30(1)： 46-49.

[34]CoorlsonBD.Covariancematrixestimationerrorsanddiagonalloadinginadaptivearrays[J].IEEETransactionsonAerospaceandElectronicSystems, 1988， 24(7)： 397-401.

[35]MaN,GohJT.Efficientmethodtodeterminediagonalloadingvalue[J].AcousticsSpeechandSignalProcessing, 2003， 15(4)： 341-344.

Improvement of Source Number Estimation Method for Single Channel Signal

DONG Zhi, HU Junpeng, HUANG Zhiping

(School of Mechatronitics and Automation, National University of Defense Technology, Changsha 410073, China)

Source number estimation methods for single channel

signal are studied and the improvement for each method is proposed in this paper. The singlechannel datais converted to multi-channel form by delay process. Then the algorithms used in the array signal processing, such as Gerschgorin’s disk estimation (GDE) and minimum description length (MDL), are introduced to estimate the source number contained within the received signal. The MDL method, which is based on information theoretic criteria (ITC), obtains a better performance than GDE at lowSNRcondition, but it has no ability to handle the signals that contained with colored noise, while the GDE method can overcome the influence of colored noise. But its performance at lowSNRhas been less than satisfactory. Based on the above consideration, this paper makes improvement on these two methods. A diagonal loading technique is employed to ameliorate the MDL method and a jackknife technique is introduced to optimize the data covariance matrix to improve the performance of GDE method. The results of simulation experiment show that the boosting we put forward makes the performance of original methods get improvement largely.

singlechannel; source number estimation; jackknife; information theoretic criteria (ITC); Gerschgorin’s disk estimation (GDE); minimum description length (MDL)

1671-7449(2017)03-0227-08

2016-11-17

董 志(1979-)， 男， 讲师， 博士， 主要从事网电空间测控研究.

TN911.7

A

10.3969/j.issn.1671-7449.2017.03.008