磁显微测量超导带材表面电流密度分布
李园园, 丁 然, 王三胜, 任道远, 李 方, 杨吉成, 霍可佳, 李 天
(1. 北京航空航天大学 微纳测控与低维物理教育部重点实验室, 北京 100191;2. 北京航空航天大学 航天器磁学与超导技术联合实验室, 北京 100191;3. 山东大学 控制科学与工程学院, 山东 济南 250061)
磁显微测量超导带材表面电流密度分布
李园园1,2, 丁 然3, 王三胜1,2, 任道远1,2, 李 方1,2, 杨吉成1,2, 霍可佳1,2, 李 天1,2
(1. 北京航空航天大学 微纳测控与低维物理教育部重点实验室, 北京 100191;2. 北京航空航天大学 航天器磁学与超导技术联合实验室, 北京 100191;3. 山东大学 控制科学与工程学院, 山东 济南 250061)
基于缺陷周围磁场异常变化的检测原理, 通过磁场检测和运动控制的结合, 建立了基于霍尔传感器和三维机械运动平台的缺陷区域检查和定位系统. 利用该系统对浸泡在液氮中的超导带材BI2121(长5 cm宽1 cm)进行磁显微测量, 可以观察超导带材自场分布. 根据毕奥萨伐尔定律, 磁场值经过二维傅里叶逆运算确定电流密度分布, 观察电流密度异常分布推断出被测样品缺陷的位置和大小. 实验结果表明霍尔探头扫描显微镜是一个诊断超导体特性有用的工具, 为无损检测技术提供一种快速简便的方法.
超导带材; 磁显微测量; 磁场分布; 电流密度; 无损检测
0 引 言
伴随着超导技术的蓬勃发展, 超导材料的应用也越来越广泛. 对超导材料的检测也成为了超导技术研究的关键之一. 由于材料缺陷的存在, 会使超导的性能大大下降甚至消失, 所以对超导材料中阻碍电流流动缺陷的研究尤为重要. 为了制备出较长的高温超导材料, 且具有尽可能大而规则的临界电流分布, 需要找到一种快速、 无损的检测超导材料质量的方法. 有两种方法可以测量超导带材中的电流分布情况, 分别是接触和非接触式的测量方法.
接触式测量方法是直流电输运4探针测量法, 即4个探针与超导材料相接触. 这种测量方式会导致超导材料局部遭到‘损坏’, 与非接触式测量方法相比测量速度较慢. 很多种测量方法都可以实现非接触式测量: ① 磁光成像[1-3], 使用一个法拉第薄膜可视化磁通密度的值. 薄膜根据磁通量密度垂直分量值来改变光的偏振. 这种测量方法非常快, 它提供了一个良好的空间分辨率,但获得磁场值不是很准确, 从而影响了超导电流的准确计算. ② 扫描霍尔探头测量法[4-8], 由一个固定在移动平台上的单霍尔传感器或者平面梯度传感器组成, 样品可以被一个外部磁场源 (永久磁铁或电磁铁) 磁化. 这种方法提供了一个良好的空间分辨率和高精度磁通密度值, 但测量速度没有磁光成像快. ③ 霍尔探头阵列测量法[9-11], 由几个霍尔效应探测器组装而成, 可以同时在几个点上测量磁场. 这种技术测量速度是非常快的,但空间分辨率非常低,因为各个传感器之间距离约0.6 mm. ④ 磁扫描测量法[12-14], 除磁铁是固定在霍尔传感器的正上方之外, 它类似于霍尔探头扫描测量法. 磁铁作用是磁化样品. 它的优势是与以前的方法相比使用磁铁更小. 然而,磁铁随着霍尔传感器一起移动, 会导致样品磁通量密度值的波动. ⑤ 扫描超导量子干涉仪(SQUID)显微镜(SSM)测量法, 由于其具备磁场测量的高灵敏度和高空间分辨率, 是用于观察超导电流分布及缺陷最有效的系统. 使用SSM系统, 已经观察到RE123微桥样品中电流流动和研究了缺陷对电流的影响[15-17]. 然而, 由于SQUID传感器的磁化饱和, 测量施加高的输运电流(几十到几百安培)的涂层导体自场分布是很困难的.
综合以上考虑, 我们设计了一种基于霍尔探头扫描法来研究和观察超导带材Bi2212表面电流密度分布的实验装置, 并在此基础上进一步设计了一种可以从宏观微观两方面观察超导带材表面电流分布的显微装置, 正在进行中. 目前的设备基于缺陷周围磁场异常变化的检测原理, 通过磁场检测和运动控制的结合, 建立了基于霍尔传感器和三维机械运动平台的缺陷区域检查和定位系统. 在满足速度和精度后, 可精确地测量超导电流密度值. 实验中首先将超导带材浸泡在液氮中冷却, 充分冷却后通过恒流源给超导带材通入恒定电流, 使其产生自发磁场, 通过测量自发磁场值, 经过二维傅里叶逆运算计算确定电流密度值, 通过连续扫描观察到产生电流缺陷的位置和大小.
1 实验装置
基于霍尔探头扫描法系统主要由三维机械运动平台、 霍尔传感器以及数据采集与储存3个部分组成. 整个系统结构如图 1 所示, 实物示意图如图 2 所示.
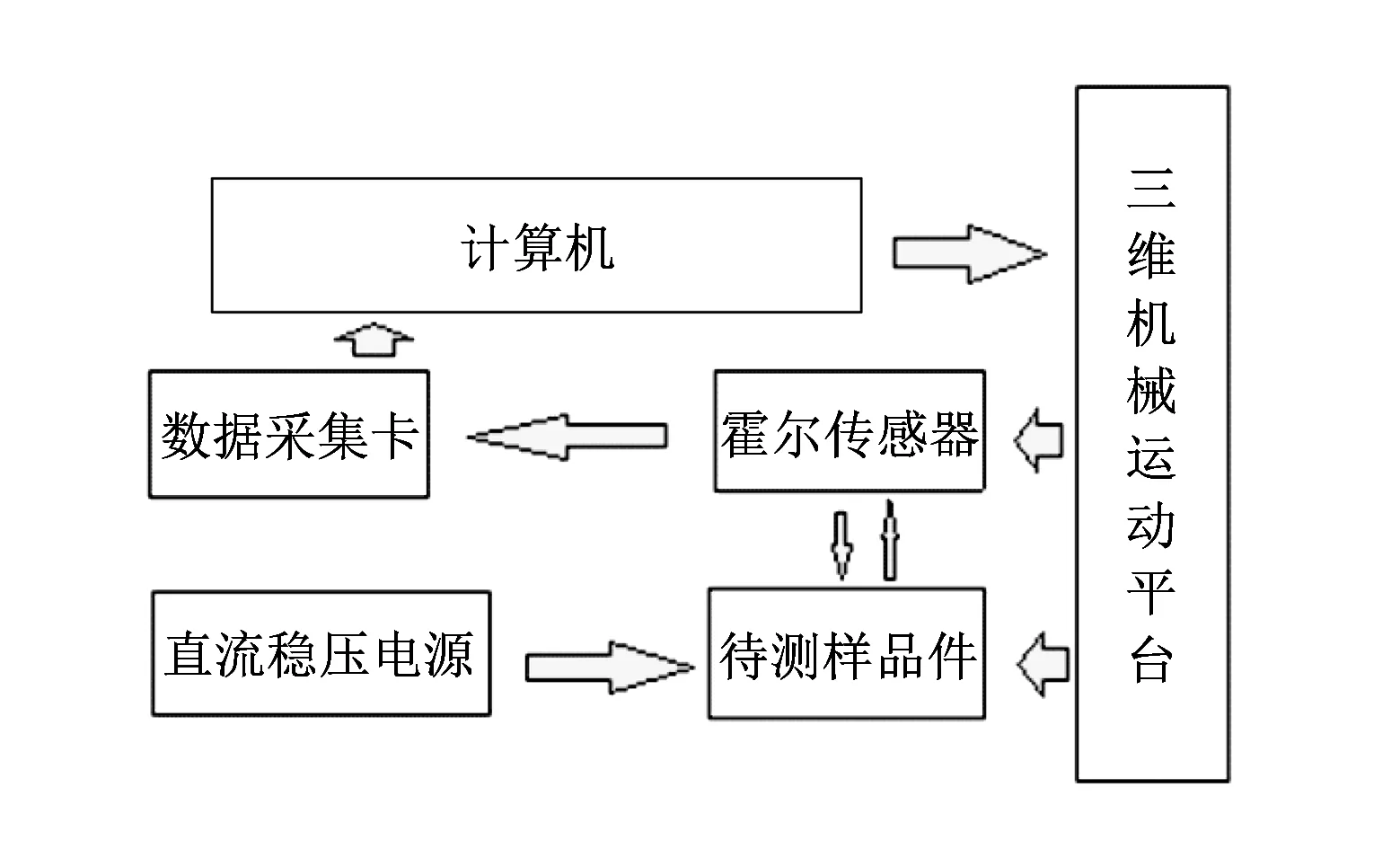
图 1 测试系统结构图Fig.1 Test system structure
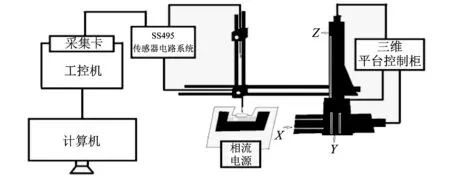
图 2 霍尔探头扫描法实物示意图Fig.2 Schematic diagram of hall probe scanning method
1.1 三维机械运动平台
三维机械运动平台扫查装置由5部分组成: 上位机(计算机)、 下位机(单片机系统)、 步进电机驱动器及步进电机、 机械运动装置及试样平台. 由计算机发送控制指令至单片机(步进电机控制器), 单片机发送控制脉冲至步进电机驱动器驱动步进电机转动, 步进电机转动通过齿轮带转换为直线运动驱动试样平台完成指定动作.XYZ3轴单轴的重复定位精度为5 μm, 3个轴组合后的重复定位精度可以达到20 μm. 上位机的主界面主要负责完成与步进电机控制器的通讯、 控制指令的发送、 一些运动参数的设置、 运动方式的选择、 数据的采集和发送等.
1.2 扫描霍尔传感器
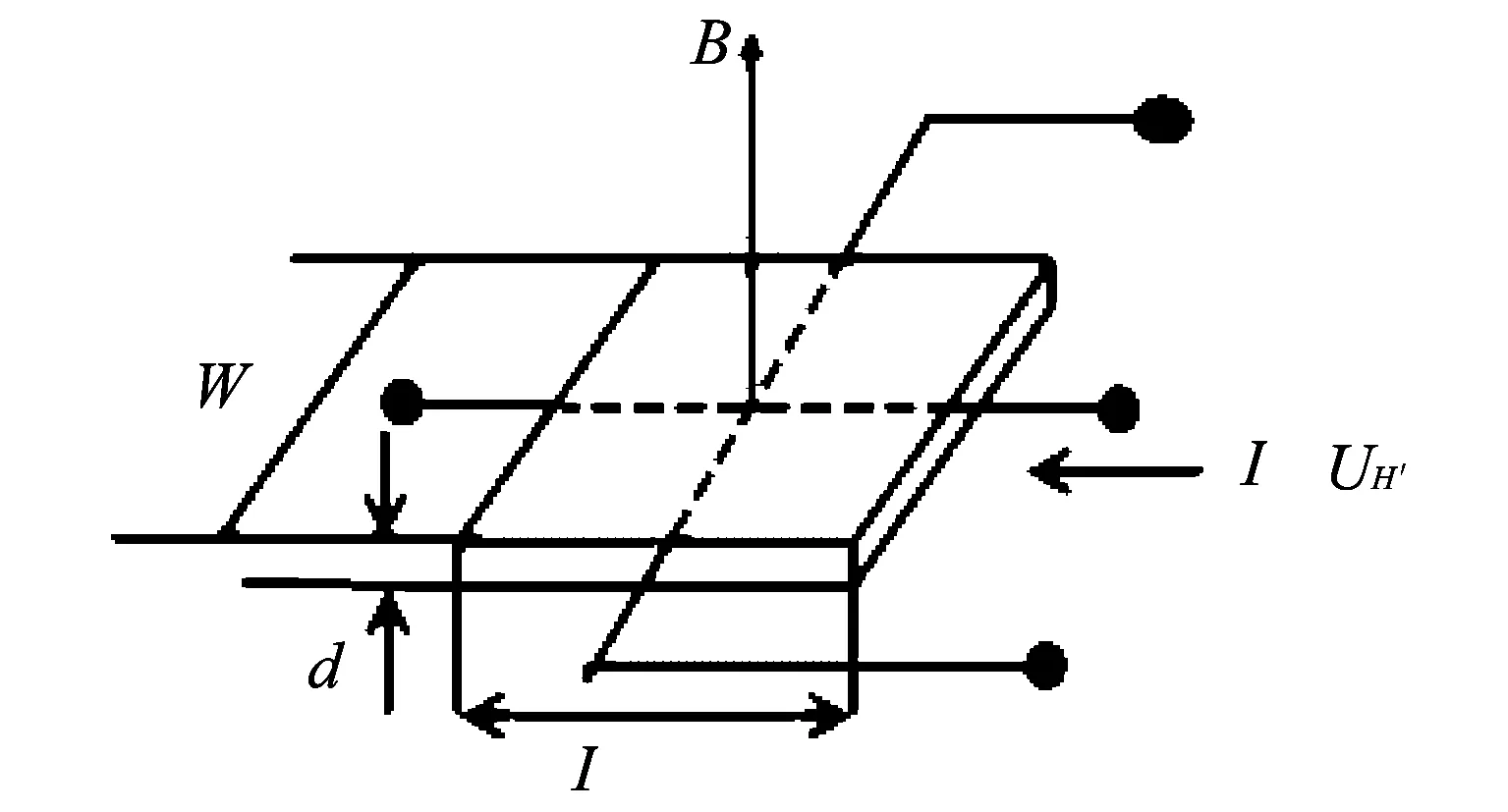
图 3 霍尔效应原理图Fig.3 Schematic diagram of hall effect
霍尔效应原理: 在均匀磁场中放入一块板状金属导体, 当在金属板通电流时, 金属板上下表面之间会出现横向电势差, 如图 3 所示. 具有霍尔效应的元件称为霍尔元件, 霍尔式传感器由霍尔元件组成. 测量时, 霍尔元件的3个引脚分别接到电源、 地和输出端的电压表, 通电后将霍尔探头放入被测磁场中让磁力线垂直于霍尔探头表面, 读出电压表的数值, 即可以从校准曲线上查得相应的磁感应强度值. 使用前, 一定先让器件在通电的状态下保持一段时间, 使之达到稳定的工作状态.
超导带材必须平行固定在样品台上, 将超导带材完全浸泡在液氮中, 使其充分冷却, 带材两端有触点, 通过触点接入恒流源, 从而使载流带材产生磁场. 霍尔探头固定在三维机械运动平台上, 通过调节X,Y,Z轴, 使霍尔探头接近待测超导带材上并与之垂直. 为了减少误差, 应用差分法, 使用两个探头组成平面梯度, 一个位于三维机械运动平台下方来测量样品和外界的磁场, 另一个位于上方来测量外界磁场.
1.3 数据采集和储存

图 4 MPS-010601数据采集卡的实物图Fig.4 Physical map of MPS-010601 data acquisition card
在定量无损检测领域, 数据采集系统是必不可少的. 在整个检测系统中, 数据采集系统完成数据的A/D转换、 数据的分析处理、 数据的存储等工作. 为实现对霍尔探头输出信号的采集、 处理, 设计了一种基于MPS-010601数据采集卡的数据采集系统, 如图 4 所示, 在数据采集卡的前端加入了由AD620组成的差分放大电路. 为了消除霍尔探头在0磁场下输出的偏置电压, 用两个霍尔探头的输出作为差分输入信号的两个输入端.
数据采集和存储是由上位机控制界面控制的, 在控制位移平台移动之前, 把相应的参数设置好, 选是否采样的选项, 打开串口, 点击开始按钮, 在位移平台开始按照运动指令运动的同时, 将会进行数据的采样. 采样的方式是: 采集位移平台所走点阵中的每个点的数据. 在位移平台运动结束后, 点击保存数据, 选择合适的保存路径, 数据会自动保存为一个TXT文档. 然后根据自己的需要处理所保存的数据即可. 数据处理应用多次测量取平均值方法, 每扫描一个点采集10个值, 然后求平均值.
2 实验结果与分析
1) 应用上述方法, 对一个直径为3.0 cm的圆柱磁铁上方的磁场进行测量, 证明我们测试系统的有效与可行性. 为了得到整体磁场分布, 测量范围为5×5 cm2, 样品与探头之间距离为1.0 mm. 单步运行步长为0.5 mm, 所以x轴和y轴上分别采集100个点, 即组成100×100的点阵扫描. 对数据进行处理, 画出磁场三维伪云图, 如图 6 所示. 磁场最强的区域是圆柱上表面磁铁的轮廓, 该图已清楚看到圆柱所在位置. 圆柱周围磁场逐渐减弱, 且具有很好的连续性. 有力证明了实验方法的正确性.
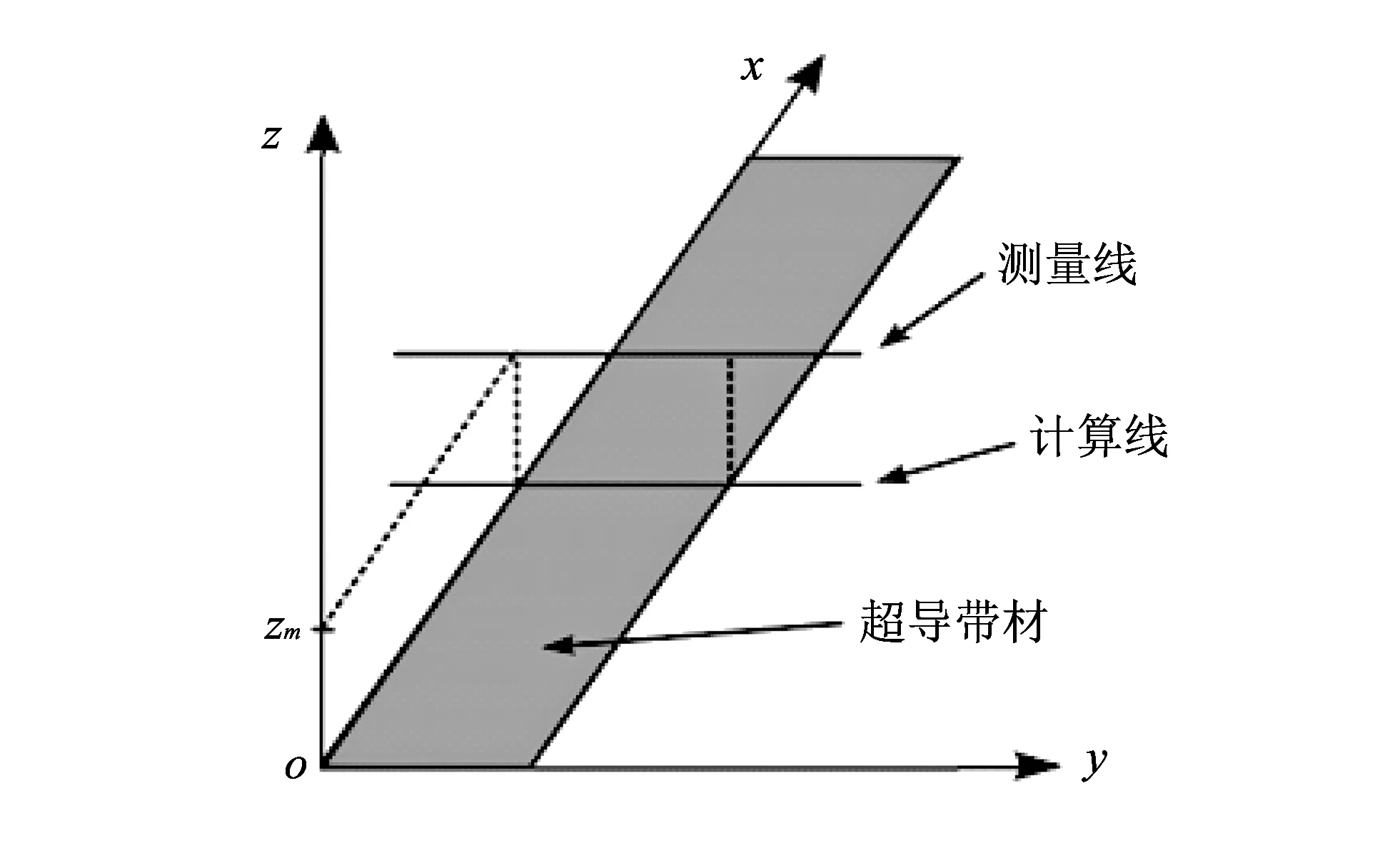
图 5 测量方法的表示Fig.5 Representation of the measurement method
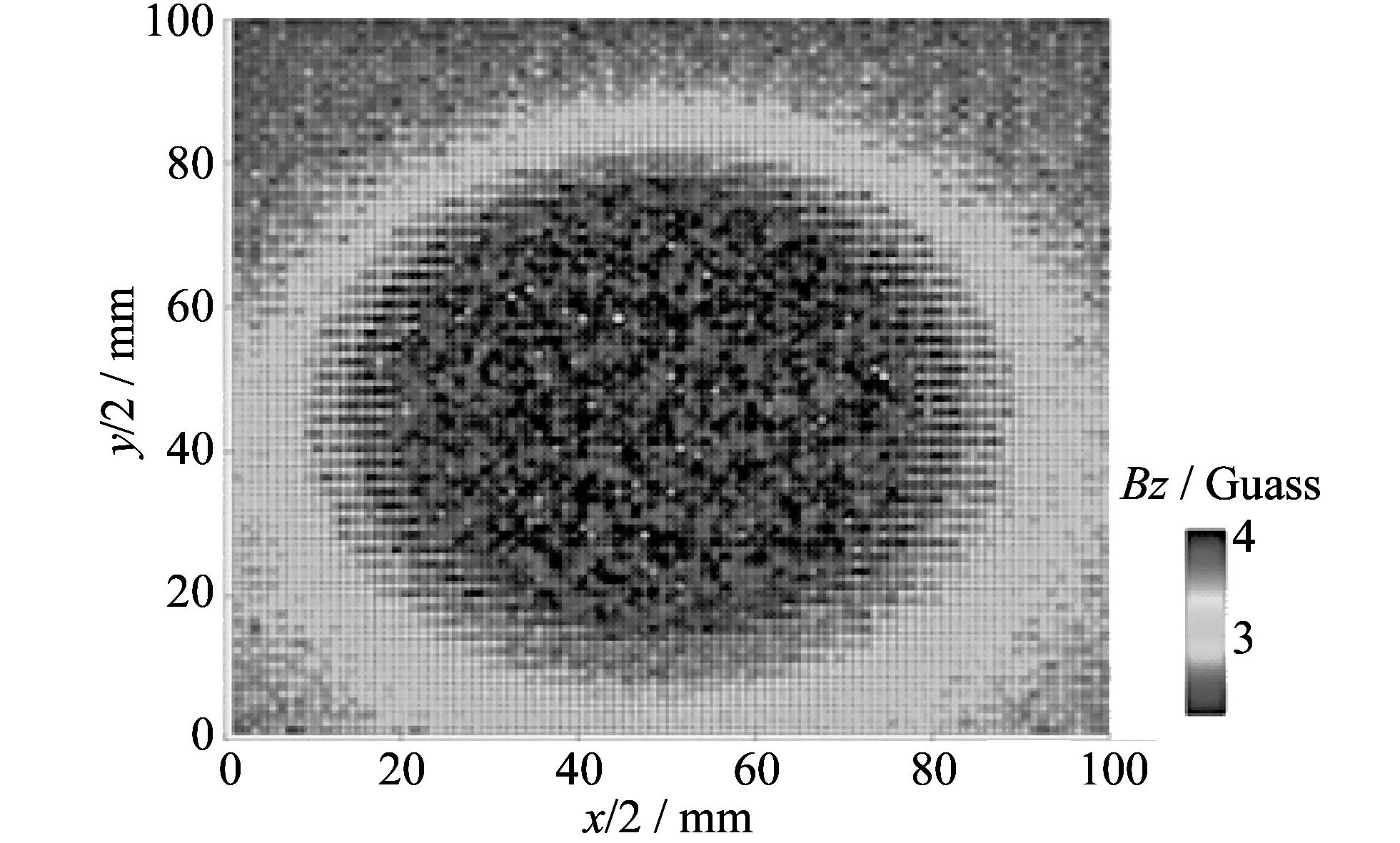
图 6 圆柱形磁铁磁场分布图Fig.6 Magnetic field distribution of cylindrical magnet

图 7 (a)从带材表面中观察到的自场分布, (b)理论计算仿真出的磁场分布. (c)由(a)二维傅里叶逆运算得到的电流分布图Fig.7 (a) the distribution of the self field observed from the surface of the strip; (b) the theoretical calculation of the magnetic field distribution; (c) by the (a) two-dimensional Fourier inversion of the current distribution
2) 用霍尔探针扫描法对BI2121超导带材(长5 cm宽1 cm)进行测量. 超导带材浸泡在液氮中, 充分冷却后通入60 A的恒定直流电流, 霍尔传感器尽可能接近超导带材, 在x轴与y轴上, 等间距分别取100个点, 测量带材磁通量密度Bz分量,Bz三维伪云图如图 7(a) 所示, 不同颜色代表不同的磁场强度. 根据毕奥萨伐尔定律, 带材两侧距离相等处, 磁场大小相等而方向相反. 尽管在纵向方向扫描步长是0.5 mm, 一个非均匀场分布和两个磁场渗透可以观察到. 由于外界周围磁场干扰的存在, 磁场分布有些许的波动, 不是绝对的平滑. 我们进行了理论计算, 并画出相应的理论计算模型, 如图 7(b) 所示, 理论与实验结果相一致. 因为超导电流密度是关于超导带材磁通量密度的函数, 应用傅里叶逆运算计算电流密度的分布, 如图7(c)所示. 获得了不同位置处具有高空间分辨率的电流密度强度分布图. 从图7(c)所示的电流分布图中, 可以确定电流的分布, 单位为A/cm. 不同区域之间, 电流互相渗透. 电流较均匀地分布在超导带材的所有区域.
3) 人为在超导带材中制造一些缺陷, 实物如图8(a)所示, 黑色三角形区域为带材的缺陷部分. 对有缺陷的超导带材进行测量, 电流密度分布如图8(b)所示, 单位为A/m. 电流密度的强度用彩色云图实现可视化. 呈三角形状的区域表明没有电流值, 因此,电流流动受到某种缺陷的干扰, 此外,电流密度的云图表示的红色区域是高于平均水平值的, 因为三角形区域缺陷的存在, 带材中可以使电流流动的有效面积减少, 而施加的电流大小不变, 所以电流密度会变大. 这些结果表明,使用霍尔探针扫描法可以直观确定缺陷的位置, 大小和形状.
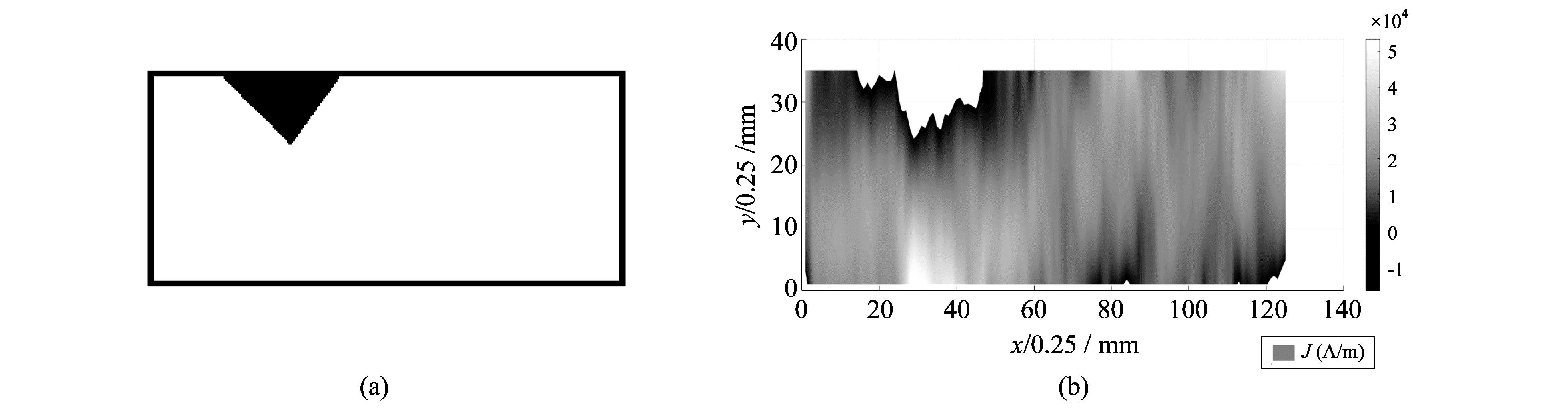
图 8 (a)图表示有缺陷的超导带材实物图, (b)有缺陷的超导体电流密度分布图 Fig.8 (a) shows the defective superconducting strip material, (b) the current density distribution of the defective superconductor
3 结 语
通过磁场检测和运动控制的结合, 建立了基于霍尔传感器和三维机械运动平台的缺陷区域检查系统, 对浸泡在液氮中的超导带材Bi2212(长5 cm宽1 cm)进行磁场测量, 可以观察超导带材自场分布和电流分布, 通过连续扫描也可以观察到带材缺陷的位置和大小. 这些结果表明霍尔探头扫描显微镜是一个诊断超导体特性有用的工具.
[1] Johansen T, Baziljevich M, Bratsberg H. Direct observation of the current distribution in thinsuperconducting strips using magneto-optic imaging[J]. Physical ReviewB, 1996, 54(22): 16264-16269.
[2] Rinke Wijngaarden, Spoelder H, Surdeanu R, et al. Deter-mination of two-dimensional current patterns in flat superconductors from magneto-optical measurements: an efficient inversion scheme[J]. Physical Review B, 1996, 54(9): 6742-6749.
[3] Ch Jooss, Albrecht J, Kuhn H, et al. Magneto-optical studies of current distributions in high-Tc superconductors[J]. Reports on Progress in Physics, 2002, 65(5): 651-788.
[4] Kohei Higashikawa, Kei Shiohara, Yoshihiro Komaki. High-speed scanning hall-probe microscopy for two-dimensional characterization of local critical current density in long-length coated conductor[J]. Physics Procedia, 2012, 27(0): 228-231.
[5] Higashikawa K, Inoue M, Kawaguchi T. Scanning hall-probe microscopy system for two-dimensional imaging of critical current density in re-123 coated conductors[J]. Physica C: Superconductivity, 2011, 471(21-22): 1036-1040.
[6] Jaeun Yoo, Yonghwan Jung, Jaeyoung Lee. Scanning hall probe measurements of field distributions of a coated conductor under applied fields[J]. Superconductor Science and Technology, 2006, 19(12): 1291-1296.
[7] Carrera M, Amoros J, Granados X, et al. Computation of current distribution in YBCO tapes with defects obtained from hall magnetic mapping by inverse problem solution[J]. IEEE Transactions on Applied Superconductivity , 2011, 21(3): 3408-3412.
[8] Polak M, Barnes P M, Mozola P, et al. Critical current in YBCO coated conductors in the presence of a macroscopic defect[J]. IEEE Transactions on Applied Superconductivity, 2009, 19(3): 2921-2924.
[9] Ho-Sup Kim, Sang-Soo Oh, Nam-Jin Lee. Nondestructive measurement of critical current distribution of smbco coated conductor using hall probe[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(3): 1537-1540.
[10] Grimaldi G, Bauer M, Kinder H. Continuous reel-to-reel measurement of critical currents of coated conductors[J]. Applied Physics Letters, 2001, 79(26): 4390-4392.
[11] Furtner S, Nemetschek R, Semerad R, et al. Reel-to-reel critical current measurement of coated conductors[J].Superconductor Science and Technology, 2004, 17(5): 281-286.
[12] Hengstberger F, Eisterer M, Zehetmayer M, et al. Assessing the spatial and field dependence of the critical current density in YBCO bulk superconductors by scanning hall probes[J]. Superconductor Science and Technology, 2009, 22(2): 025011-025017.
[13] Zehetmayer M, Fuger R, Eisterer M, et al. Assessment of the local supercurrent densities in long superconducting coated conductors[J]. Applied Physics Letters , 2007, 90(3): 032506-032509.
[14] Hengstberger F, Fuger R, Eisterer M, et al. Ho-mogeneity of supercurrent flow in coated conductors[J]. Physica C: Superconductivity, 2007, 460-462, Part 2(0): 1397-1398.
[15] Koyanagi K, Kiss T, Inoue M, et al. Measurement of local current flow around transverse defects in YBCO film by use of scanning SQUID microscope[J]. Physica C, 2006, S445-448: 677-681.
[16] Kiss T, Inoue M, Shoyama T, et al. Visualizing transport properties in IBAD based YBCO coated conductors by multiple analysis techniques[J]. IEEE Trans. Appl. Superconductivity, 2007, 17: 3211-3214.
[17] Masayoshi Inoue, Kenji Abiru, Yoshihiro Honda, Observation of Current Distribution in High- Superconducting Tape Using Scanning Hall-Probe Microscope[J]. IEEE Transactions on Applied Superconductivity, 2009, 19: 2847-2850.
[18] Julien Leclerc, Kevin Berger, Bruno Douine, Jean eveque, Field mapping measurements to determine spatial dependence of critical current density in YBCO tapes[J]. Physica C: Superconductivity, 2013, 492: 158-164.
Measurement of Surface Current Density Distribution in Superconducting Tapes by Magnetic Microscopy
LI Yuanyuan1,2, DING Ran3, WANG Sansheng1,2, REN Daoyuan1,2, LI Fang1,2, YANG Jicheng1,2, HUO Kejia1,2, LI Tian1,2
(1. Beihang University Key Laboratory of Micro-nano Measurement, Manipulation and Physics,Ministry of Education, Beijing 100191, China;2. Beihang University Joint Laboratory Magnetism and Superconducting Technology on Spacecraft, Beijing 100191, China;3. Shandong University School of Control Science and Engineering, Jinan 250061, China)
Based on the detection principle of variations magnetic field around defects, the detection and location system using hall sensor and 3D mechanical motion platform is established through the combination of magnetic field detection and motion control. The system was used to measure the magnetic field of BI2121 (long is 5cm wide is 1cm) immersed in liquid nitrogen. Therefore the self-fields distribution of superconducting tapes can be observed. According to Biot-Savart law, current density distribution is determined by two-dimensional Fourier inverse operation. Therefore, observing the abnormal distribution of the current density can determine the location and size of the defects in the samples. The experimental results show that the hall probe scanning microscope is a useful tool to diagnose superconductor characteristics. It provides a fast and simple method for nondestructive testing.
superconducting tape; magnetic microscopy measurement; field distribution; current density; nondestructive testing
1671-7449(2017)03-0254-06
2017-01-20
国家国防科技工业局资助项目 (JSJC2013601****)
李园园(1992-), 女, 硕士生, 主要从事磁场测量与无损检测技术等研究.
o514.2
A
10.3969/j.issn.1671-7449.2017.03.012

