基于线分量幅度的圆极化天线测试方法的修正
王道雨, 汪 敏, 徐 诺, 吴 文
(南京理工大学 JGMT国防重点学科实验室, 江苏 南京 210094)
基于线分量幅度的圆极化天线测试方法的修正
王道雨, 汪 敏, 徐 诺, 吴 文
(南京理工大学 JGMT国防重点学科实验室, 江苏 南京 210094)
本文讨论了基于线分量幅度的圆极化天线测试方法, 介绍了这种方法测试轴比的原理, 首次指出了这种方法不能判定主极化旋向的问题, 并提出了采用两个一般性能的圆极化参考天线来判定旋向的修正方案. 此外针对实际测试中的特殊情况进行了修正完善. 最后实际测量了自行设计的双频双圆极化天线阵列, 测试与仿真结果保持了良好的一致性, 从而表明了该修正的正确性、 有效性与实用性.
测试方法修正; 线分量幅度; 圆极化天线特性参数; 旋向
0 引 言
圆极化天线特性参数的测试方法有线分量法、 圆分量法和极化图法等[ 1]. 实际中高极化隔离的线极化天线更容易得到, 因而线分量法的应用更为广泛. 例如, 文献[2,3]通过线分量的幅度和相位得到了圆极化天线的轴比、 方向图等特性, 这种方法亦称为线圆变换法. 然而一般天线测试场中相位测试会受到测试设备的限制, 误差会比较大. 文献[4-7]则仅利用线分量幅度即得到了轴比等特性, 这种方法的优势在于幅度更容易精测, 从而提高了测试精度. 然而该方法由于缺少了相位信息造成了主极化旋向无法判定, 当前未有文献对此问题进行了分析. 本文对此进行分析, 给出解决方案进行修正, 同时针对该方法实际测试中的特殊情况完善了测试处理方案.
修正后的测试方法准确性提高, 实用性增强. 利用该方法对自行设计的双频双圆极化天线阵列进行实际测量, 实测结果与仿真结果保持了良好的一致性, 满足科研、 工程等对圆极化天线测试的需求.
1 测试原理
极化是电磁理论中一个重要的概念, 它表征在与波的传播方向垂直的平面内, 电磁矢量随时间变化的轨迹[8]. 当该轨迹形状为直线、 圆和椭圆时, 可分别称之为线极化、 圆极化和椭圆极化. 其中线极化和圆极化是椭圆极化的特例. 极化图、 倾角、 轴比和旋向是极化椭圆的主要参数, 如图 1 所示.
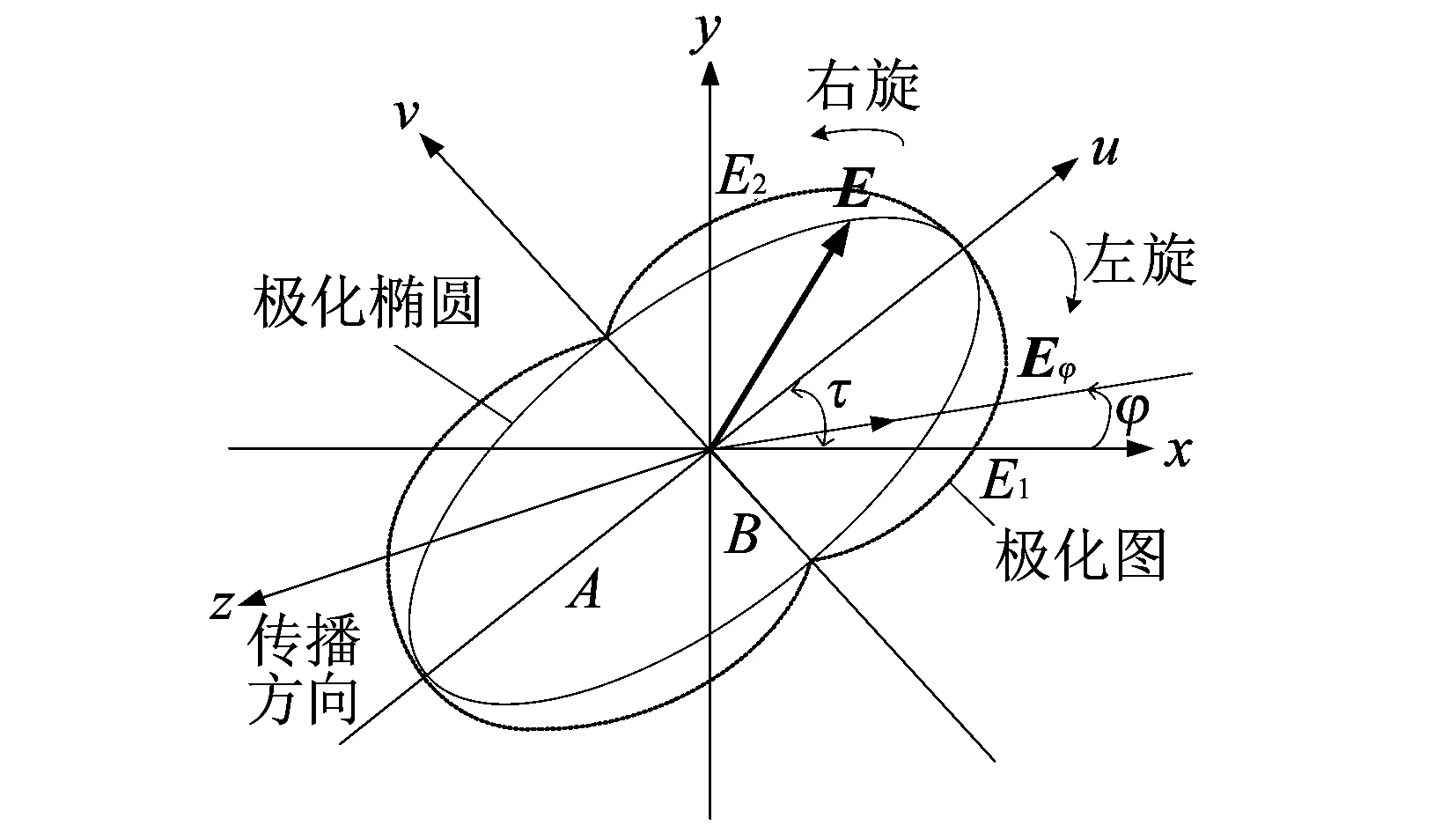
图 1 极化椭圆Fig.1 Polarization ellipse
极化图反映了任意电场矢量E在φ方向的最大投影Eφ, 如图 1 所示, 其中Eφ与φ的关系式表示为[4]
(1)
式中: E1, E2分别为水平极化波振幅和垂直极化波振幅; δ为E1, E2之间的相位差.
事实上, Eφ就是xy平面中旋转的线极化天线对φ方向的场强响应, 极化图的最大值和最小值分别与极化椭圆的最大值和最小值重合. 给出任意两组正交的线分量幅度, 例如旋转线极化天线测得φ=0°, 90°, 45°, 135°两组正交的场强响应E1, E2, E3, E4, 代入式(1)联立, 可得到
(2)
图 1 中极化椭圆的倾角τ是长轴2A与x坐标轴的夹角, 它与E1, E2和δ之间满足
(3)
定义极化椭圆的长轴2A和短轴2B之比为轴比, 记为RA, 用dB表示为20log(RA). 当RA=0dB时为圆极化; 当RA=∞时则为线极化. 轴比与E1, E2和δ的关系可表示为
(4)
因此, 通过E1, E2, E3, E4得到cosδ后, 代入式(3)和式(4)即可得到倾角和轴比.
根据以上分析, 利用线极化天线仅测试两组正交的线分量幅度, 无需相位测试, 即可得到圆极化天线的轴比特性, 由于幅度更容易精测, 从而提高了测试精度.
2 旋向判定的辅助修正
椭圆极化波的旋向若与传播方向z成左手螺旋关系(图 1 中顺时针旋转), 称为左旋圆极化; 若与z成右手螺旋关系(图 1 中逆时针旋转), 则称为右旋圆极化. 具体旋向信息可以通过E1和E2间的相位差δ得到:δ∈ (-π,0) 时则为右旋圆极化, δ∈ (0,π) 时为左旋圆极化.
式(2)中cosδ∈[-1,1],arccosδ∈[0,π], 从而无法判定δ∈[ 0,π]还是δ∈[-π,0]. 这说明只测4组幅度值丢失了重要的相位差信息, 从而无法判断主极化旋向, 这个问题尚未有文献提及.
本文提出: 采用两个旋向相反、 结构相同的圆极化参考天线对待测天线的旋向进行判定, 两个参考天线分别测试待测天线的幅度, 测得幅度大的参考天线的旋向即为待测天线的旋向. 这里无需采用高极化纯度的圆极化天线, 只需一般性能的圆极化天线即能够进行幅度对比, 在实际中是容易实现的.
获得主极化旋向信息后, 圆极化天线的方向图可通过如下获得. 任意电场矢量E可分解为左旋圆极化分量L和右旋圆极化分量R, 它们的幅值与线分量幅度满足如下关系:
(5)
而轴比RA也可以用L, R表示为(假设L>R)
(6)
联立式(5),式(6)可得
(7)
因此待测圆极化天线的方向图可用式(7)表示, 分别对应主极化和交叉极化分量.
3 特殊情况的修正
表 1 给出了E1/E2、δ与合成椭圆极化波的典型关系. 从表 1 中可以看出一些特殊情况:
1) 当E1/E2=∞时,E2=0, 此时无论δ为何值, 合成的椭圆极化波都为水平线极化波;
2) 当E1/E2=0时,E1=0, 此时无论δ为何值, 合成的椭圆极化波都为垂直线极化波;
3) 当E1/E2=1,δ=0或±π时, 合成的椭圆极化波也为线极化波, 极化方向在τ=±45°方向;
4) 当E1/E2=1,δ=±π/2, 合成的椭圆极化波为圆极化波.
实际测试中电场波接近特定方向线极化如上述1),2)两种情况时
(8)
代入式(2)中分子和分母都接近于0, 容易出现较大误差, 即|cosδ|=0/0可能出现大于1的情况, 从而轴比处理误差较大. 而情况3)下
(9)
此时式(2)中cosδ可准确处理, 同时2τ误差较小. 因而对于1),2)两种情况, 可通过情况3)先求出准确的cosδ′, 再求得准确的轴比RA. 即令
(10)
则
(11)
(12)
(13)
实际测试中电场波接近4)的情况也会出现, 此时E1=E2=E3=E4, 圆极化性能好, 但式(3)中τ的分子和分母同时接近于0, 造成τ=0/0误差较大. 而先利用式(2)准确求出δ=±π/2, 再通过另一轴比表达式[9]可准确求出轴比, 即:
(14)
4 实验验证
运用修正后的测试方法对自行设计的双频双圆极化微带阵列进行多次测试, 根据天线用于发射和接收时特性间的互易性[10], 测试时将待测圆极化天线作为接收天线随转台转动, 线极化喇叭天线作为发射天线保持不动, 测试示意图如图 2 所示.
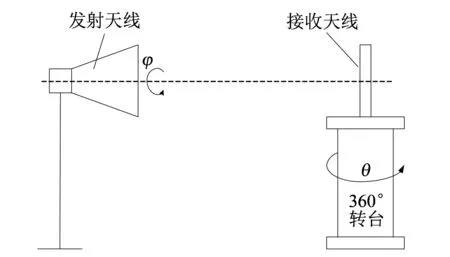
图 2 测试示意图Fig.2 Test schematic
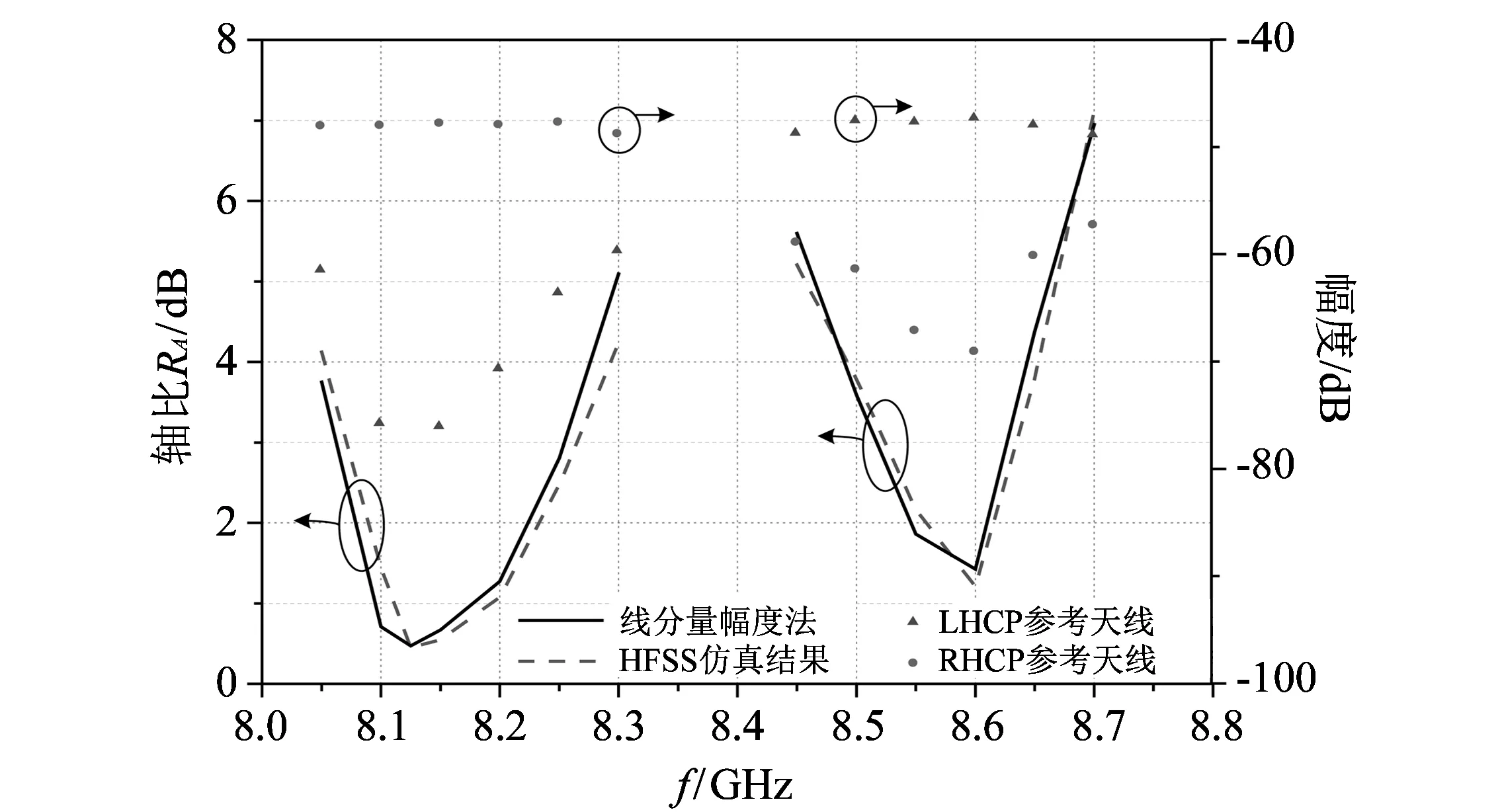
图 3 轴比随频率变化曲线(φ=0°, θ=0°)和参考天线所测幅值Fig.3 Curves of axial ratio versus frequency (φ=0°, θ=0°) and amplitudes measured by reference antennas
将线极化天线的极化位置分别置于φ=0°, 90°, 45°, 135°方向, 测取4组线极化幅度, 计算出轴比并与HFSS仿真结果进行比较, 如图 3 所示, 可以看出低频段和高频段上测试的轴比随频率变化曲线与仿真曲线吻合得都很好. 另外采用两个结构相同的左右旋圆极化参考天线对待测天线进行幅度对比测试, 从图 3 中可以看出在低频段右旋圆极化(RHCP)参考天线测得的幅度电平大于左旋圆极化(LHCP)参考天线, 在高频段则相反, 从而可以判断出低频工作时主极化旋向为右旋圆极化, 高频工作时主极化旋向为左旋圆极化. 最后通过线分量幅度法所得轴比处理出两个中心频率(8.2 GHz, 8.6 GHz)处的主极化归一化方向图, 如图 4, 图 5 所示, 可见实测结果与仿真结果也保持了很好的一致性. 由此可见该修正是正确、 实用且有效的.
5 结 论
本文依托南京理工大学JGMT国防重点学科实验室的微波暗室, 对基于线分量幅度的圆极化天线测试方法进行了修正. 原有的测试方法并不能判定主极化旋向, 因而提出利用一般性能的圆极化参考天线来判定待测天线的旋向, 另外对测试中的线极化和圆极化等特殊情况进行分析, 完善了处理方法. 最后进行了实验验证, 结果表明这种修正具有正确、 方便、 效率高、 准确性强等优点, 满足科研、 工程等对圆极化天线测试的基本需求.
[1] 毛乃宏, 俱新德. 天线测量手册[M]. 北京: 国防工业出版社, 1987.
[2] 尚军平, 傅德民, 蒋帅, 等. 圆极化天线特性参数测量方法[J]. 西安电子科技大学学报, 2009, 36(1): 106-110. Shang Junping, Fu Demin, Jiang Shuai, et al. Method for measuring the charac-teristic parameter of the circular polarization antenna[J]. Journal of Xidian University, 2009, 36(1): 106-110. (in Chinese)
[3] Toh B Y, Cahill R, Fusco V F. Understanding and measuring circular polarization[J]. IEEE Transaction on Education, 2003, 46(3): 313-318.
[4] 林昌禄. 天线测量技术[M]. 成都:成都电讯工程学院出版社, 1987.
[5] 张晓平, 周怀安. 一种圆极化天线极化特性的幅度精测方法[J]. 航天器环境工程, 2009, 26(1): 67-70. Zhang Xiaoping, Zhou Huaian. An accurate test method for circular polarized antenna[J]. Spacecraft Environment Engineering, 2009, 26(1): 67-70.(in Chinese)
[6] 李南京, 冯引良, 王建飞, 等. 利用线极化天线快速测量圆极化天线轴比的方法[J]. 红外与激光工程, 2013, 42(8): 2216-2220. Li Nanjing, Feng Yinliang, Wang Jianfei, et al. Fast measuring axial ratio of circular polarization antennas based on linear polarization antenna[J]. Infrared and Laser Engineering, 2013, 42(8): 2216-2220.(in Chinese)
[7] 李文廷, 韦高, 仲兆宇, 等. 圆极化天线轴比的测量方法[J]. 电子设计工程, 2014, 22(7): 77-81. Li Wenting, Wei Gao, Zhong Zhaoyu, et al. Method for measuring the axial ratio of circular polarization antennas[J]. Electronic Design Engineering, 2014, 22(7): 77-81.(in Chinese)
[8] 谢处方, 饶克谨. 电磁场与电磁波[M]. 第4版. 北京: 高等教育出版社, 2006.
[9] 方大纲. Antenna theory and microstrip antennas[M]. 北京:科学出版社, 2010.
[10] 钟顺时. 天线理论与技术[M]. 北京:电子工业出版社, 2011.
Corrections of the Test Approach for Circular Polarization Antenna Based on Linear Component Amplitudes
WANG Daoyu, WANG Min, XU Nuo, WU Wen
(JGMT Ministerial Key Laboratory, Nanjing University of Science and Technology, Nanjing 210094, China)
The test approach for circular polarization antenna based on linear component amplitudes has been discussed in this paper. The principle of the approach is introduced for testing axial ratios. Then it is the first time to point out the problem that the approach cannot determine the rotation sense of co-polarization. And a correction scheme has been proposed to determine the rotation sense by using two circular polarization reference antennas with general performance. Beside saccording to the exceptional circumstances in practical test, the amendment and improvement have been given. Finally, a self-designed dual-band dual-circular polarization antenna array has been tested practically. The test and simulated results maintain good consistency, which shows the correctness, validity and practicability of the corrections.
test corrections; linear component amplitudes; circular polarization antenna characteristic parameters; rotation sense
1671-7449(2017)03-0266-05
2016-12-19
国家自然科学青年基金资助项目(61401208)
王道雨(1991-), 男, 硕士, 主要从事天线理论与设计的研究.
TN820.5
A
10.3969/j.issn.1671-7449.2017.03.014

