基于多目标线性模糊模型的军品供应商选择

郭健杰，王凤忠

（1.军事交通学院 研究生管理大队，天津 300161；2.军事交通学院 军用车辆系，天津 300161）

基于多目标线性模糊模型的军品供应商选择

郭健杰1，王凤忠2

（1.军事交通学院 研究生管理大队，天津 300161；2.军事交通学院 军用车辆系，天津 300161）

采用模糊集理论，将多个产品与多个供应商结合，建立一个模糊多目标线性模型，帮助决策者找到每个供应商的适当订单，并提高军方采办的成本，质量和服务上的绩效。

军品供应商；模糊多标准决策；多来源多产品

1 引言

军方采购系统选择供应商主要由后勤系统打分，方法比较单一。选择过程中主观成分较多，标准不全面，目前主要集中在质量、成本、交货速度等方面，没有形成全面、系统、科学的综合评价体系。在未来的信息化战争中，不断满足创新需求，选择最优质的供应商，实现采购“多赢”，已是军方采购系统不得不考虑的问题。然而，供应商选择是多标准决策问题，其中的标准具有不同的相对重要性[1]。一些因素可能会发生冲突，为了选择最佳供应商，必须对这些有形和无形因素进行权衡。本文提出一个模糊多目标线性模型来处理这个问题，能够将多个产品与多个供应商相结合，将所建立的模型逐步转换为单个目标，在存在与输入相关的信息模糊时，军方基于该方法能作出更合理的决策。

2 问题描述

2.1 供应商生产、供应中所产生的不确定性

目前，普遍使用的确定性模型主要缺点是不能处理嵌入在真实系统中的随机性。军事供应链中的决策需要考虑众多的不确定性。在系统内部，不确定性可能是由人、机器或系统相关的问题引起的。外部因素也可能给决策带来不确定性，包括需求变化、政策、市场力量和竞争行为等。模糊逻辑和工具是将不确定性纳入决策模型的分析方法[2]。模糊逻辑允许分析中的信息不完整，用近似的推理来分析系统，在解决供应链产品相关问题中高效、方便，并且模糊工具比其他模型更容易开发、实现和修正。模糊逻辑非常适合分析生产过程中的不确定性，为最终的决策提供有力的参考。

2.2 产品配置与采购过程中“多对多”的问题

在军事供应链的产品配置中，成品通常由许多部件组成，这些部件中的每一个都可以由来自不同地理位置的各种供应商提供。为了提高产品功能，配置变更的挑战是找到提供优质组件的合适的零件供应商，并能最有效地满足这些要求[3]。换句话说，基于消费者或工程要求，对于特定产品需要适当的部件供应商组合，以便决定哪个供应商将提供哪个部件。“供应商组合”的目的是评估所有潜在的零件供应商，并确定最优的组合[5]。即使是多次采购，现在的研究通常只考虑单一产品的供应商选择，本文旨在解决多种产品选择多个供应商的“多对多”的问题，对多源多产品的采购进行建模分析。

2.3 多重采购下的供应商选择

很多研究只针对单一产品的供应商选择，其中一个供应商可以满足所有买家的需求，军队的采购量大、范围广，单一的采购方式远远不能满足军队采购活动。本文讨论的是针对一个或者多个供应商的多次采购，在体积足够大的情况下，需求订单在几个供应商之间分配的情况。目前军队采购方在要求商品的品种种类齐全的同时，需求量却是时小时大。并且在军品采购中，战略型供应商都是多重采购，以满足高峰或紧急时的需求。在供货困难时，军方要求首先受到供应商的照顾，如果供应商的生产能力不足以满足高峰需求，则可能会出现瓶颈，充足的供应商资源则可以缓解军队的燃眉之急。

3 基本定义和模型构建

在军事供应商选择问题的实际情况中，采购策略的不同使得标准的权重可能不同。供应商选择问题的模糊目标受制于军方的采购计划和供应商能力的现实约束[4]。本文提出一种最大模糊多目标模型，认为目标函数之间没有差别，即假定目标同样重要，使得模糊目标的达成水平与期望的相对权重或决策者的期望相近[3]。这种模糊模型使军方不仅可以考虑信息的不精确性，同时在计算每个供应商的订单数量以及匹配目标函数的相对重要性时，也考虑供应商的限制。

3.1 评估因子权重

正梯形数可以定义为图1所示的（n1，n2，n3，n4），并且隶属函数μn（x）表示为：

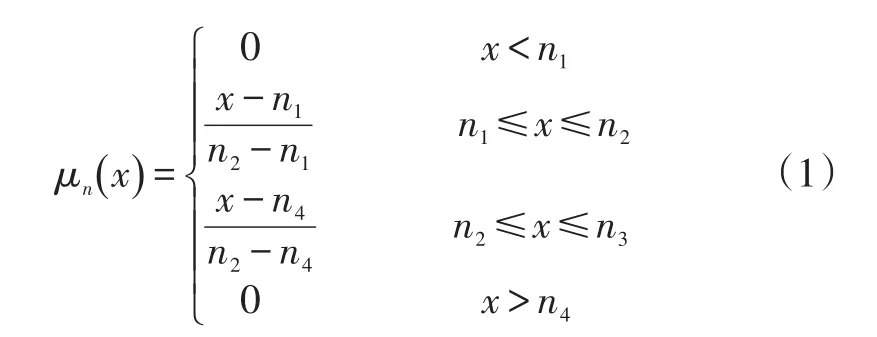
对于梯形数，如果n1=n2，那么该数被称为三角形模糊数。

图1 梯形数n

语言变量是其值以语言术语表达的变量。例如，如果“温度”作为语言变量，则其术语集合可以是“非常低”，“低”，“舒适”，“高”和“非常高”。在本文中，采购方使用图2所示的语言值来评估模糊多目标线性模型中因子的权重。

图2 每个因素的重要性权重的语言变量

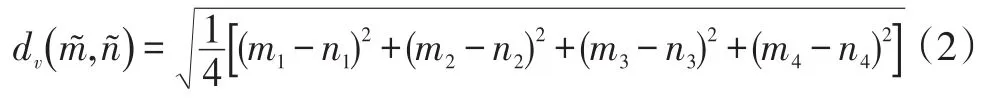
假设决策组具有B个决策者，b=1,2，...，B，并且对于供应商选择问题考虑一组j个标准，j=1,2，...，n。然后，每个标准的聚合模糊权重（wj）可以表达为：

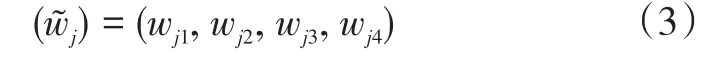
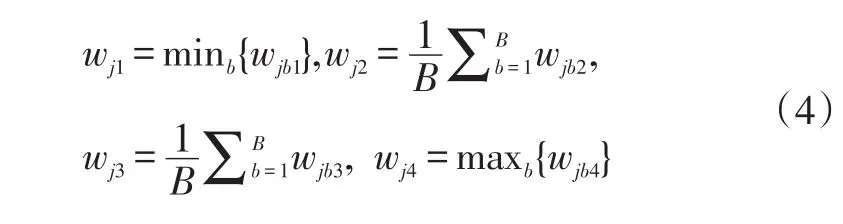
类似于AHP和TOPSIS方法并考虑语言变量（lv），选择标准的模糊正理想等级（FPIR-A*）和模糊负理想等级（FNIR-A-）[5]，可以定义为：A*=lv*，A-=lv-，根据图2所示的语言变量，选择标准的FPIR和FNIR可分别表示为“非常高”（0.8,0.9,1.0,1.0）和“非常低”（0.0,0.0, 0.1,0.2）。可以通过顶点法来计算每个标准的聚合模糊权重（wj）与理想等级之间的距离。

确定接近系数以计算所开发的模糊多目标线性模型每个因子的权重。其中是到FNIR的距离，是到FPIR的距离。对接近系数进行归一化，每个因子的最终权重（w）j可以计算为：

3.2 单一产品的模糊多目标供应商选择模型

单个产品的供应商选择问题的一般多目标模型可以表示如下：

约束条件：

其中Z1,Z2,...,Zk是否定目标或标准类成本，延迟交货等，Zk+1,Zk+2,...,Zn是正面目标或标准，例如质量、销售服务等。Xd是满足买方需求、供应商能力等约束的一组可行解。

供应商选择问题的典型线性模型是min Z1；max Z2，Z3。

约束条件：

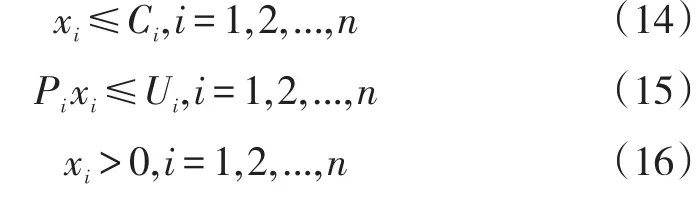
其中D是期间的需求，xi是从第i个供应商购买的单元数，pi是来自第i个供应商的每单位净购买成本，Ci是第i个供应商的容量，Ui是从第i个供应商购买的预算，Fi是第i个供应商质量水平的百分比，Si是第i个供应商按时交货的百分比，n是供应商的数量。

以上制定了三个目标函数：设定为价格成本最小，总质量最优和按时交货所购买的产品。约束条件（13）确保满足选择需求，约束条件（14）表示每个供应商的订单数量应该等于或小于其容量。约束条件（15）表示每个供应商的预算限制，约束条件（16）订单不为负数。

3.3 一般多目标模型选择

首先介绍供应商选择的一般多目标模型，然后讨论此决策问题的适当运营商。一般的线性多目标模型可以表示为：

找到以变换形式xT=[x1，x2，...，xn]写成的向量x，其最小化目标函数Zk和最大化目标函数Zl表示如下：

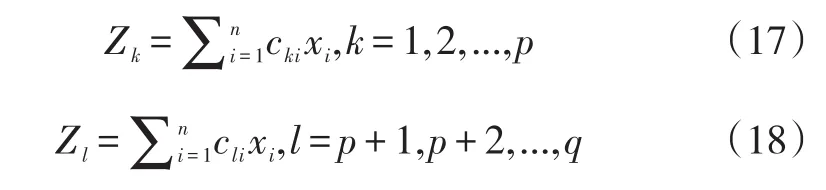
约束条件为：

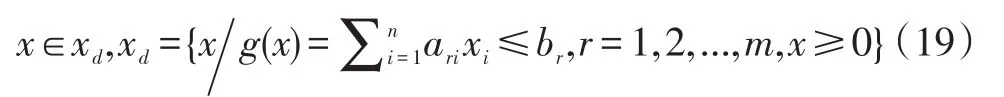
其中cki,cli,ari和br是模糊值。

将每个目标函数Zj分解为其最大值和最小值来制定模糊线性规划：

每个目标函数Zj对于到线性地改变，所以它可以被认为是具有线性隶属函数 μzj(x)的模糊数，如图3所示。

结果表明，具有模糊目标和模糊约束的线性规划问题可以表示如下：

查找向量x以满足：

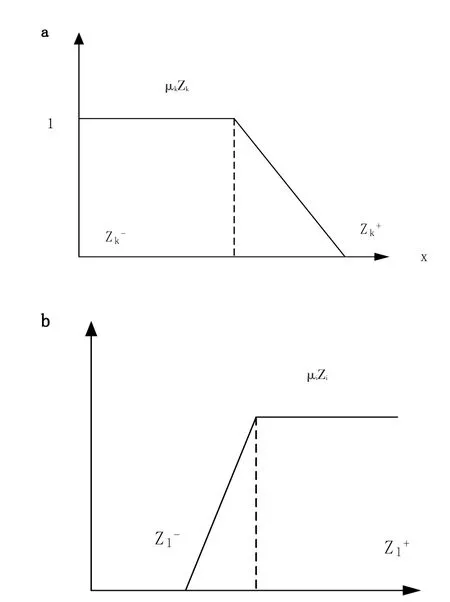
图3 目标函数作为模糊数：（a）min Zk和（b）max Zl

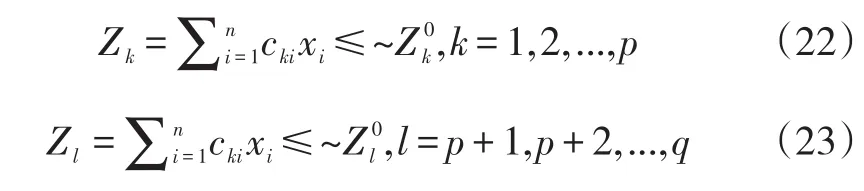
约束条件为：

在这个模型中，符号“~”表示模糊环境。约束集中的符号“≤~”解释为：“基本上小于或等于”，同理“≥~”语言解释为：“基本上大于或等于”。和是决策者达到的理想期望水平。

根据偏好或满意度是线性的，假设隶属函数，则最小化目标（Zk）和最大化目标（Zi）的线性关系给出如下：

模糊约束的线性隶属函数为：

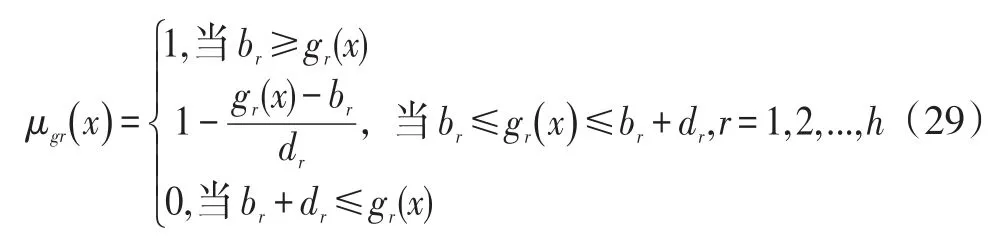
dr是主观选择的常数，表示允许违反第r个不等式约束（公差间隔）的限制。

3.4 约束条件下的最优解

在模糊模型中，使用加权相加的方法，为不同的标准分配不同的权重，一个模糊解由所有模糊集的交集给出，表示模糊目标或模糊约束。所有模糊目标和模糊约束的解可以表示为：

最优解（x*）由下式给出：

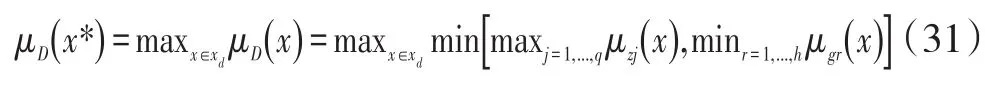
加权相加模型：

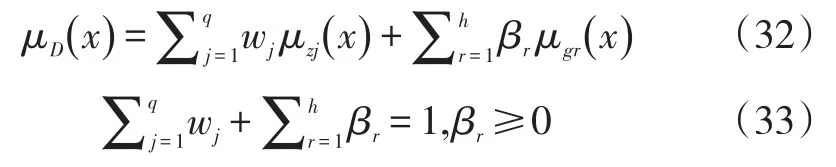
其中wj和 βi是表示模糊目标和模糊约束之间的相对重要性的加权系数。以下简单的单目标程序设计等价于上述模糊模型：

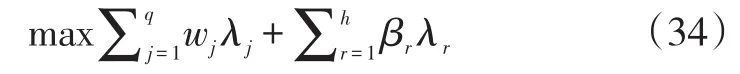
约束条件为：

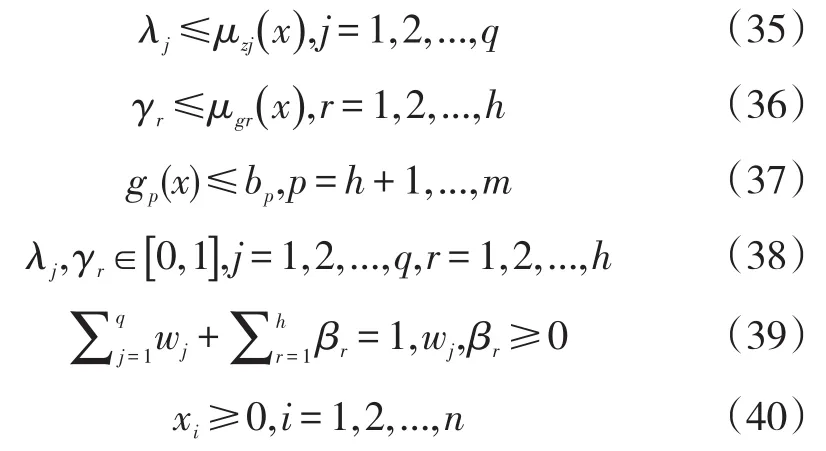
通过限制条件最终确定模型的最优解，此模型反应到采购决策过程中，可表达为：在预算、供应商容量等约束条件下，计算得出定量数据集，最终确定每个供应商和每个产品的最小、最大订单数量和产品上支出的最大允许预算。

4 结论

本文提出了一个完整的基于模糊多目标线性模型的供应商选择方法。首先提出了具有多个产品或供应商的模糊供应商选择模型、模糊目标函数、模糊约束和模糊系数，然后将所建立的模型逐步转换为单个目标。根据决策者的偏好，把选择标准的权重看成相等或不相等的重要性。并使用不同权重的选项，运用表示为梯形模糊数的语言值来评估因子的权重[6]。与AHP或TOPSIS方法类似，该方法被表示为模糊正理想等级和模糊负理想等级，以计算因子的权重。最后，设计了模糊多目标线性模型，以克服供应商选择问题，并为每个供应商分配每个产品的最佳订单量。

[1]梁世翔.采购实务[M].北京:人民交通出版社,2007.

[2]李兰芳.模糊层次分析法在供应商选择中的应用[J].宁夏工程技术,2005,4(4):349-350.

[3]程红彦.供应商管理绩效综合评价模型研究[J].模糊系统与数学,2012,(1):74-78.

[4]李波.新的军队采购制度下供应商管理策略研究[D].广州:华南理工大学,2009.

[5]张思颖.模糊层次分析法在供应商评价选择中的应用[J].物流技术,2007,30(12):61-64.

[6]Chen Tung,Cand Ching Torng.L.A fuzzy approach for supplier evaluation and selection in supply chain management[J].International Journal of Production Economics,2006,102(2):289-231.

[7]Chen C.Extensions of the TOPSIS for group decision-making under fuzzy environment[J].Fuzzy Sets&Systems,2000,114(1): 1-9.

M ilitary Product Supp lier Selection Based on Multi-objective Linear Fuzzy Model

Guo Jianjie1,Wang Fengzhong2
(1.Graduate StudentBrigade,Military Transportation Academy,Tianjin 300161;
2.Military VehicleDepartment,Military Transportation Academy,Tianjin 300161,China)

In this paper,we used the fuzzy set theory to bind multiple products and suppliers and built a fuzzy multi-objective linear model which could help decision makers determine the suitable order for each supplier and enhance the cost,quality and service performance of themilitaryparty.

military productsupplier;fuzzymulti-standard decisionmaking;multi-origin product

E233

A

1005-152X(2017)05-0162-04

10.3969/j.issn.1005-152X.2017.05.036

2017-03-25

郭健杰，男，硕士研究生，研究方向：装备采购管理。