利用离散余弦变换与梯度脸的人脸光照处理*

聂祥飞，杨志军，何 雪

(重庆三峡学院 电子与信息工程学院，重庆 404000)



利用离散余弦变换与梯度脸的人脸光照处理*

聂祥飞，杨志军，何 雪

(重庆三峡学院 电子与信息工程学院，重庆 404000)

针对光照变化对人脸识别效果带来的严重影响，提出了一种基于离散余弦变换和梯度脸的人脸光照处理方法。该方法首先将人脸图像变换到对数域，在对数域中计算离散余弦变换，舍弃部分低频系数，再计算其离散余弦反变换。然后用梯度脸(Gradientfaces)算法对人脸图像的高频细节成分进行增强。在人脸识别阶段，采用主成分分析法提取人脸特征，运用基于余弦距离的最近邻分类器进行分类判别。在Yale B正面人脸库和CUM PIE人脸库上进行实验，实验结果表明该方法可以削弱人脸光照的影响，适用于光照鲁棒的人脸识别，合理地选择相关参数，人脸识别率分别能够达到100%和96.25%。

离散余弦变换；梯度脸；人脸光照处理；人脸识别

0 引言

在人脸识别中，因为相同人脸在不同光照条件下的差异大于不同人脸在相同光照条件下的差异，所以光照问题一直是人脸识别中面临的主要挑战之一[1]。一般情况下，解决人脸识别中光照问题的方法主要分为三类：提取光照不变特征、光照变化的建模、光照条件标准化等[2]。

(1)提取光照不变特征。其基本思想是提取人脸图像中不随光照变化或至少对光照变化不敏感的特征。如商图像、去噪模型、自商图像法[3]等。ELDP[4]等提出一种对光照具有不变性的算法,该算法使8方向的图像边缘信号生成光照不敏感特征，取得了很好的识别效果。Zhang[5]等提出梯度脸算法，该算法考虑相邻像素间的潜在联系，在梯度域中提取了光照不变特征，但该方法没有进行降维处理，因此计算量大，计算复杂。

(2)光照变化的建模。其主要思想是在一个合适的子空间或流形中表示光照引起的变化，然后对人脸的特征估计模型参数。如主成分分析(PCA)[6]、线性判别分析(LDA)[7]、子空间投影法[8]、光照锥法[9]和基于球面谐波基图像的方法[10]等。这类方法需要大量不同光照条件下的人脸图像作为训练样本，因此在实际应用中受到一定的限制。

(3)光照条件标准化。该方法是对人脸图像作预处理操作，规范化为标准形式，获取鲁棒的光照人脸图像，如经典的直方图均衡法[11]、伽玛矫正、同态滤波、对数变换等。Chen[12]等提出的离散余弦变换算法，在对数域中对人脸图像进行离散余弦变换，舍弃部分低频系数，对重建后的人脸图像进行识别，但该算法没有考虑图像的高频成分。光照条件标准化的方法对光照引起的人脸变换具有一定的补偿作用，但是识别效果增强不明显。

在本文中，人脸光照处理的框图如图1所示。首先,将人脸图像变换到对数域，在对数域中，对输入人脸图像作离散余弦变换[13]，舍弃部分低频系数，然后作离散余弦反变换。当完成人脸图像归一化后，利用梯度脸[5]对人脸图像的高频细节部分进行增强并提取光照不变的人脸特征。本文方法综合考虑了人脸图像的高频成分和低频部分，不仅舍弃了部分的光照分量，同时也对反射分量进行了一定的增强。由于光照处理的目的是为了提高人脸识别率，因此其处理的有效性通过人脸识别率来表征。

图1 人脸光照处理框图

1 算法介绍

1.1 人脸图像的对数变换

根据光照模型，任意灰度人脸图像I(x,y)可以看成是反射分量和光照分量的乘积[14]：

I(x,y)=R(x,y)L(x,y)

(1)

其中，R(x,y)即低频，对应图像的快变化部分，L(x,y)即高频，对应图像的慢变化部分。对式(1)两边取对数，得：

lnI(x,y)=lnR(x,y)+lnL(x,y)

(2)

从式(1)和式(2)可以看出，在空间域中原图像的反射分量和光照分量是相乘的关系，而在对数域中却变成了相加的关系。因此人脸图像在对数域中进行光照处理就是削弱光照分量对应的低频部分，其处理效果等同于高通滤波。

1.2 梯度脸算法

梯度脸[5]算法的主要思想如下：

对于灰度图像I(x,y)，像素点(x,y)在x方向的邻域点为(x+Δx,y)，则有：

I(x+Δx,y)=R(x+Δx,y)L(x+Δx,y)

(3)

式(3)-式(1)得：

I(x+Δx,y)-I(x,y)=R(x+Δx,y)L(x+Δx,y)-

R(x,y)L(x,y)

(4)

由于L近似光滑且变化缓慢，则有：

I(x+Δx,y)-I(x,y)≈(R(x+Δx,y)-R(x,y))L(x,y)

(5)

当Δx趋于0时，式(5)取极限有：

(6)

同理在图像的y方向有：

(7)

式(7)除以式(6)得：

(8)

其中Iy为人脸图像在y方向上的梯度∂I(x,y)/∂y，Ix为人脸图像在x方向上的梯度∂I(x,y)/∂x，Ry为人脸图像反射分量在y方向上的梯度，Rx为人脸图像反射分量在x方向上的梯度。根据假设理论，R是光照不变分量，因此Iy与Ix的比值也是光照不变的。

图像的梯度脸定义如下：

G=arctan(Iy/Ix)

(9)

其中G∈[π,-π]。实际应用中，为了计算梯度脸，首先需要计算人脸图像在x方向、y方向的梯度值，为了能够成功地计算梯度值，首先需要用高斯核函数光滑人脸图像，即人脸图像与高斯核函数卷积后再分别计算x方向和y方向的梯度。高斯核函数的表达式为：

(10)

其中σ为高斯核函数的标准差。

2 实验

2.1 人脸图像的对数变换

本文采用Yale B人脸库和CUM PIE人脸库进行实验。Yale B人脸数据库共包含10个人的9种不同姿态，每种姿态又包含64种不同的光照。因为本文只研究光照处理问题，所以只选择使用正面姿态下不同光照的人脸图像作为实验样本。实验时，人脸图像的尺寸是128×128，且将所有图像按照入射光的不同角度分为5个子集。子集1共包含70个样本,其角度小于12°。子集2共包含120个样本，其角度位于13～25°之间。子集3共包含120个样本，其角度位于26～50°之间。子集4共包含140个样本，其角度位于51～77°之间。子集5共包含190个样本，其角度大于77°。CUM PIE人脸数据库共包含68个人的41 368个人脸图像，本文算法主要解决的是光照问题，因此选择正面人脸光照组(C27)作为训练图库。该光照组共有1 428个人脸库，所有图片均裁剪为64×64大小。

2.2 参数的选择

实验时，对式(10)中高斯核函数σ参数和离散余弦变换后舍弃的低频系数个数的不同取值进行了实验。在Yale B人脸库中实验时，通过挑选，最终确定高斯核函数σ参数为0.57和DCT舍弃的低频系数个数为19时获得最好的人脸识别率。在CUM PIE人脸库中实验，通过挑选，单独使用DCT变换时，DCT舍弃系数个数为19时获得最好的识别效果，单独使用梯度脸算法时，高斯核函数σ参数为 0.55时获得最好的识别效果。

人脸图像经过光照处理后，规范化其均值和方差分别为0和1，运用主成分分析法提取人脸特征时，其特征向量数为50。

2.3 实验结果

在Yale B正面人脸库中的实验结果如图2所示。图2中显示的是人脸图像光照处理后的效果对比图，其中第一行是原图，第二行是经离散余弦变换处理后的人脸图像，第三行是经本文方法处理后的人脸图像。从图2可以看出，经本文所提方法光照处理后的人脸图像，可以削弱不同角度的光照对人脸图像的影响，对光照具有一定的鲁棒性。

图2 Yale B人脸光照处理结果

在Yale B人脸库上的实验结果如表1所示，表1中列出了现有部分人脸光照处理算法处理后的人脸错误识别率，其中以Yale B正面人脸库的子集1作为训练集，其他子集作为测试集，且表中DCT算法与梯度脸算法的实验条件与本文方法的实验条件一致。从表1可以看出，DCT算法的最小平均错误识别率为1.58%，梯度脸算法的最小平均错误识别率为0.70%，QI的平均错误识别率为45.35%，WBCT的平均错误识别率为2.26%，LBP的平均错误识别率为23.2%，本文算法的平均错误识别率为0。

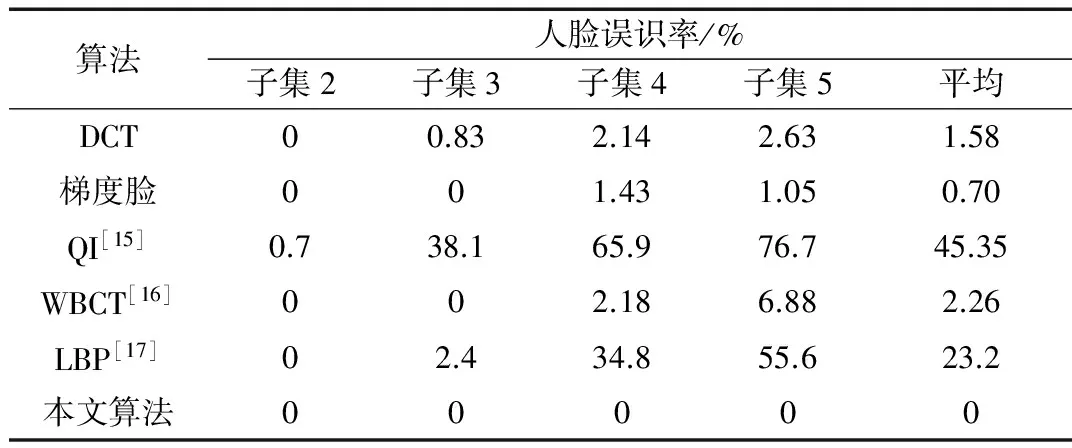
表1 不同光照处理算法的结果对比

在Yale B人脸库中的第二个实验是分别采用不同的子集作为训练集，其余子集作为测试集。当训练集为子集1时，测试子集2、子集3、子集4、子集5的识别率均为100%。子集2作为训练集时，子集1、子集3、子集4、子集5的识别率均为100%。子集3作为训练集时，子集1、子集2、子集4、子集5的识别率均为100%。子集4作为训练集时，子集1、子集2、子集3、子集5的识别率均为100%。子集5作为训练样本时，子集1、子集2、子集3、子集4的识别率均为100%。即以任一子集作为训练集，其余子集样本都能够识别。

为了进一步验证本算法的有效性，在CUM PIE数据库上进行了实验。实验时，从每个样本的21种光照中选取一个人脸图像作为训练集，其余人脸作为测试集。图3中列出了部分人脸图像以及与其相对应的本文方法处理后的人脸图像。从图中可以看出，经本文方法处理后的人脸图像保留了重要的人脸特征，这些特征对人脸识别起着重要的作用。

图3 部分CUM PIE 人脸图像及相关本文方法处理后的人脸图像

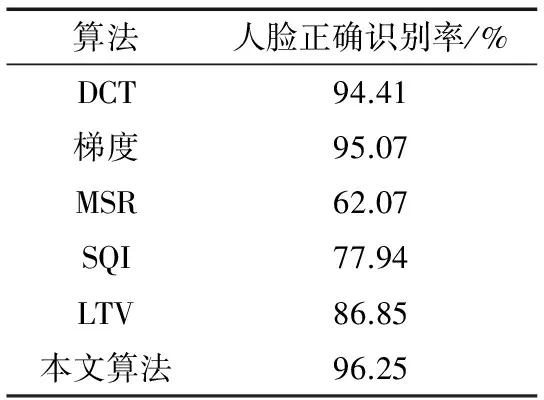
表2 不同算法的实验对比结果

表2列出了参考文献[5]的部分重要实验结果和本文算法的实验结果。其中DCT算法和梯度脸算法与本文实验条件一致。

3 结论

本文提出了一种基于离散余弦变换和梯度脸的人脸光照处理算法。该算法先将人脸图像在对数域中做离散余弦变换，舍弃部分低频系数，然后用梯度脸算法增强人脸的高频细节信息。提取人脸特征用的是主成分分析法，使用基于余弦距离的最近邻分类器进行分类判别。实验结果表明，本文所提方法光照处理后的人脸识别正确率，在Yale B人脸库中可达到100%，在PIE人脸库上为96.25%，可以有效削弱光照的影响。今后的主要工作是在更大型的人脸库上对本算法进行测试。

[1] Tao Song, Ke Xiang, Wang Xuanyin. Face recognition under varying illumination based on gradientface and local features[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2015, 10(2): 222-228.

[2] FARAJI M R, QI X. Face recognition under varying illumination based on adaptive homomorphic eight local directional patterns [J]. Iet Computer Vision, 2014, 9(3):390-399.

[3] WANG H T, LI S Z,WANG Y S, Face recognition under varying lighting conditions using self quotient image[C].Proc of IEEE International Conference on Automatic Face and Gesture Recognition, 2004:819-824.

[4] FARAJI M R, QI X. Face recognition under illumination variations based on eight local directional patterns[J]. Biometrics Iet, 2015, 4(1):10-17.

[5] ZHANG T P, TANG Y Y,FANG B , et al. Face recognition under varying illumination using gradientfaces[J]. IEEE Transactions on image processing, 2009, 18(11): 2599-2606.

[6] 周先春，孙文荣.基于自适应对数变换和PCA算法的人脸识别研究[J]. 电子技术应用，2014, 40(6):126-129.

[7] BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1997, 19(7):711-720.

[8] MANOLOVA A, TONCHEV K, BOUMBAROV O, et al. Recognition of facial images with subspace projection and dissimilarity representation [C]. IDAACS 2011: 6th International Conference on Intelligent Data Acquisition and Advanced Computing, IEEE,2011: 444-449.

[9] CHEN J, XIA C, YING H, et al. Using facial symmetry in the illumination cone based 3D face reconstruction [C]. IEEE International Conference on Image Processing, 2013: 3700-3704.

[10] ZHAO W Y, CHEN S L, ZHENG Y, et al. Lighting estimation of a convex lambertian object using redundant spherical harmonic frames[J]. Journal of Computer Science & Technology, 2013, 28(3):454-467.

[11] SHAN S, GAO W, CAO B, et al. Illumination normalization for robust face recognition against varying lighting conditions[C]. IEEE International Workshop on Analysis and Modeling of Faces and Gestures, 2003: 157-157.

[12] CHEN W, MENG JOO ER, WU S. Illumination compensation and normalization for robust face ercognition using discrete cosine transform in logarithm domain[J]. In IEEE Transactions on System,Man, and Cybernetics. Part B (Cybernetics) ,2006,36(2):458-466.

[13] VISHWAKARMA V P, PANDEY S, GUPTA M N. An illumination invariant accurate face recognition with down scaling of DCT coefficients[J]. Journal of Computing & Information Technology, 2010, 18(1): 53-67.

[14] SHAHAMAT H, POUYAN A A. Face recognition under large illumination variations using homomorphic filtering in spatial domain [J]. Journal of Visual Communication & Image Representation, 2014, 25(5):970-977.

[15] SHASHUA A, RILLIN-RAVIV T. The quotient image: class-based re-rendering and recognition with varying illuminations [J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2001, 23(2):129-139.

[16] LONG B T, LE T H. Using wavelet-based contourlet transform illumination normalization for face recognition [J]. International Journal of Modern Education & Computer Science, 2015, 7(1):16-22.

[17] AHONEN T, HADID A, PIETKAINEN M. Face description with local binary patterns: application to face recognition[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2006, 28(12):2037-2041.

Face illumination processing using discrete cosine transform and gradientfaces

Nie Xiangfei, Yang Zhijun, He Xue

(School of Electronics and Information Engineering, Chongqing Three Gorges University, Chongqing 404000, China)

Focus on the issue that the change of lighting has a serious impact on face recognition, a novel approach based on Discrete Cosine Transform (DCT) and gradientfaces for face illumination processing is proposed. Firstly, face images are transformed into logarithm domain in which DCT is calculated and some low-frequency coefficients are discarded. After that, inverse DCT is calculated. Then, the details of high frequency apart of face image are enhanced by gradientfaces arithmetic. In the process of face recognition, Principal Component Analysis (PCA) is used to extract face features, and the nearest neighbor classifier based on cosine distance is used to classify. Experiments have been carried out on Yale B face database and CUM PIE face database, the experimental results show that this method can weaken the effect of illumination and be suitable for illumination robust of face recognition. The recognition rate can reach to 100% and 96.25% respectively for choosing reasonable parameters.

Discrete Cosine Transform (DCT); gradientfaces; face illumination processing; face recognition

国家自然科学基金资助项目(61602072)；重庆市教委科技项目(KJ121114)；重庆高校创新团队建设计划资助项目(CXTDX201601034)

TN911.73

A

10.19358/j.issn.1674- 7720.2017.11.015

聂祥飞，杨志军，何雪.利用离散余弦变换与梯度脸的人脸光照处理[J].微型机与应用，2017,36(11)：50-53.

2017-01-15)

聂祥飞(1973-)，男，博士，教授，硕士生导师，主要研究方向：智能信息处理，模式识别。

杨志军(1991-)，男，硕士研究生，主要研究方向：智能信息处理，模式识别。

何雪(1989-)，女，硕士研究生，主要研究方向：智能信息处理，模式识别。