基于有限-无限元法的CRTSⅢ板式无砟轨道系统动力参数敏感度分析

李伟

（中铁第一勘察设计院集团有限公司，陕西 西安 710043）

基于有限-无限元法的CRTSⅢ板式无砟轨道系统动力参数敏感度分析

李伟

（中铁第一勘察设计院集团有限公司，陕西 西安 710043）

CRTSⅢ型板式无砟轨道是具有完全自主知识产权的中国无砟轨道品牌，针对CRTSⅢ型板式无砟轨道车辆-轨道耦合系统动力参数的确定与优化问题，根据CRTSⅢ型板式无砟轨道系统结构特点，运用车辆-轨道耦合动力学理论，采用时域动力有限元方法，并引入无限单元法消除边界效应，建立CRTSⅢ型板式无砟轨道车辆-轨道耦合系统垂向振动模型，并编制MATLAB计算程序，利用单因素敏感性分析法分析了结构参数对车辆-轨道系统动力响应指标的敏感度，从而可为CRTSⅢ型板式无砟轨道结构动力参数的确定与优化提供理论支撑。

高速铁路；无砟轨道；耦合动力学；有限元；无限元

为了适应我国高速铁路“走出去”战略，提升我国无砟轨道技术的创新水平,打造中国无砟轨道的自主品牌。为此，在总结我国既有无砟轨道研究与应用经验的基础上，结合无砟轨道技术再创新成果，我国研发了具有完全自主知识产权的CRTSⅢ型板式无砟轨道。CRTSⅢ型板式无砟轨道是对既有无砟轨道结构的优化，创新之处主要包含：板式无砟轨道结构的限位方式、板下采用自密实混凝土作为填充材料、提高了轨道弹性以及完善了设计理论体系等。CRTSⅢ型板式无砟轨道已在成灌铁路成功铺设，迄今运营状态良好，另武汉城市圈城轨铁路已确定采用CRTSⅢ型板式无砟轨道，同时盘营客专、沈丹客专铁路也准备采用。

CRTS III型板式无砟轨道仍然主要由钢轨、扣件系统、轨道板、板下填充层及混凝土底座板等组成，其设计理论原则是“路基纵连、桥隧单元、方便维修”。路基上CRTSIII型板式无砟轨道采用的是一种柔性的纵连结构，增强轨道结构的整体性，当存在温度梯度时，柔性纵连轨道结构纵向具有一定自由伸缩能力；桥隧段单元板结构又能很好规避连续结构受温度力造成的不利影响。CRTS III型板式无砟轨道采用自密实混凝土作为填充调整层，其与轨道板粘结形成牢固的复合结构，轨道板与混凝土底座板间不再有薄弱的夹层。另外，CRTSIII型板式无砟轨道采用了“缓冲隔离层”技术，为日后实现方便维修创造了必要的条件。

随着无砟轨道的发展，国内外对无砟轨道结构参数对车辆动荷载作用下的动力响应的影响进行了大量研究[1-4]，但是对于CRTSⅢ型板式无砟轨道在车辆与轨道耦合作用下车辆-轨道系统动力响应的研究并不多见。因而本文根据CRTSⅢ型板式无砟轨道系统结构特点，运用车辆-轨道耦合动力学理论[1]，采用有限元及无限元方法，建立CRTSⅢ型板式无砟轨道车辆-轨道耦合系统动力分析模型，编制MATLAB计算程序，并对CRTSⅢ型板式无砟轨道系统结构参数对系统动力响应的影响进行计算分析，从而可为CRTSⅢ型板式无砟轨道结构动力参数的确定与优化提供理论支撑。

1 CRTSⅢ型板式无砟轨道车辆-轨道耦合系统动力分析模型

1.1 车辆系统方程的建立

将车辆系统假设为具有二系悬挂的多刚体系统，仅考虑单节车辆模型共有10个自由度[1，5，6，7]。单节高速车辆以速度v运行，其车辆系统的振动微分方程为：

式中：MV，[CV]和[KV]分别为单节列车车辆系统的质量矩阵、阻尼矩阵及刚度矩阵分别为车辆的位移、速度和加速度向量；{QV（t）}为轮轨力荷载向量。上式中各变量的表达式分别为式（2～6），其中[CV]和[KV]的表达式参考文献[8]，此处限于篇幅不赘述。

1.2 轨道系统方程的建立

用有限元法建立车辆－无砟轨道耦合系统竖向振动模型时，将钢轨视为离散黏弹性点支承二维Euler梁单元[5-7]，扣件和轨下垫板采用2节点弹簧-阻尼单元模拟，预制轨道板离散为连续黏弹性支承的二维Euler梁单元，预制轨道板下自密实混凝土采用连续地基弹簧模拟，水硬性混凝土支承层离散为连续黏弹性支承的二维Euler梁单元，混凝土支承层下路基亦采用连续地基弹簧模拟，进而建立轨道系统三层叠合梁模型，见图1。

图1 轨道系统三层叠合梁模型Fig.1 Three-layer laminated beam model of track system

钢轨、轨道板及底座板等采用2节点仅考虑节点竖向和转角两个自由度的Euler梁单元，单元长度取为离散支承点的间距l，即钢轨扣件间距。梁单元位移形函数采用Hermite 3次插值函数，梁单元质量矩阵Me、刚度矩阵Ke分别为：

钢轨、轨道板及底座板等的边界采用无限梁单元模拟以消除边界效应，以钢轨边界无限梁单元为例简要说明其原理。由于振动计算中钢轨仅取有限长度，截取后钢轨边界对计算结果有一定影响，在钢轨两端各加一3节点无限映射梁单元，可明显缩短钢轨的长度以消除边界效应，并提高模型计算效率。钢轨无限梁单元的单元质量矩阵及由支承弹性产生的单元刚度矩阵和阻尼矩阵分别为：

式中：meq，ceq，keq分别为连续弹性支承轨道的等效分布质量、钢轨支承分布阻尼及分布弹性系数。引入坐标变换，转换矩阵：

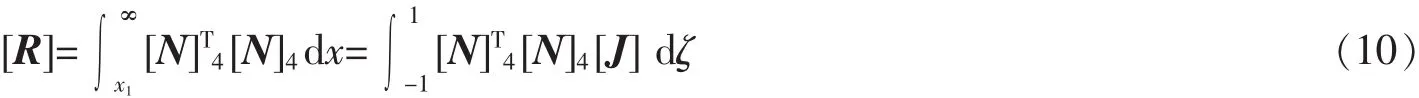
式中：[J]为坐标变换的雅克比矩阵的行列式。另由无限长梁弯曲产生的单元刚度矩阵为：

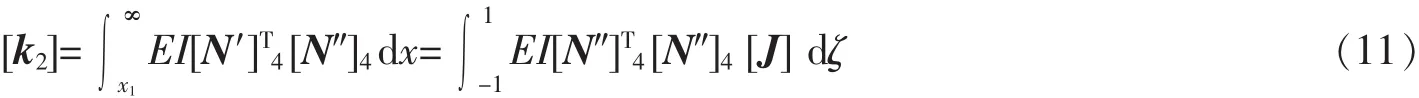
无限梁单元的单元刚度矩阵为[k1]与[k2]之和，钢轨无限梁单元的单元刚度矩阵：

将轨道系统有限单元相应的单元质量矩阵、刚度矩阵及阻尼矩阵，按照“对号入座”法组集成系统总体刚度矩阵、总体质量矩阵、总体阻尼矩阵，并通过将假设的初始轮轨力按照等效荷载节点力分配而形成初始总体荷载向量，从而得到轨道系统运动控制方程：

式中：[M]、[C]、[K]分别为轨道系统总体的质量、阻尼、刚度矩阵，{P}为广义载荷向量；{q}为广义位移向量为广义速度向量，为广义加速度向量。

1.3 车辆-轨道耦合相互作用的模拟

车辆运动方程(1)与下部轨道系统振动方程(13)不是完全独立的，而是通过轮轨接触关系互相耦合的，轮轨间Hertz非线性接触轮轨力pj（t）为：

式中：δZ，Zwj（x，t）-[zr（xpj，t）+zr0（xpj，t）]，轮轨接触常数G=3.86 R-0.115×10-8m·N-2/3（磨耗型踏面车轮）；Zwj（x，t）为t时刻第j位轮对的垂向位移；zr（xpj，t）为t时刻第j位轮对下钢轨的垂向位移；zr0（xpj，t）为t时刻第j位轮对下轨道的不平顺。

1.4 轨道不平顺的模拟

中国高速铁路无砟轨道不平顺谱采用幂函数分段拟合，各波长区段的轨道谱均采用同一表达式[8]：

式中：S（f）的单位为mm2/(1/m)；f是空间频率，1/m；A和n是拟合系数。表1为我国典型高速铁路无砟轨道不平顺的平均谱拟合系数，其中包括4段不同的拟合系数，各分段点的空间频率和对应波长如表2所示，它们适用于300～350 km/h的无砟线路。

表1 高低不平顺谱拟合系数Tab.1 Fitting coefficient of high and low uneven spectrum

表2 分段点空间频率及对应波长Tab.2 The spatial frequency of the segmentation point and the corresponding wavelength

轨道随机不平顺常采用功率谱密度函数表示，然而在车辆-轨道耦合垂向振动模型中，耦合系统激励一般采用时域输入方式，以便数值求解，因此需要根据无砟轨道高低不平顺谱密度函数转化为随里程变化的轨道高低不平顺空间样本（相应转化为时域样本）。

现轨道不平顺常用的数值模拟方法主要有：二次滤波法、三角级数法、白噪声滤波法和逆傅氏变换法等[1]。事实上，轨道不平顺功率谱是对时域采样信号通过周期图法估计而获得的，其计算核心是快速傅立叶变换。逆傅氏变换法基于功率谱快速数值算法原理，在计算方法上采用了傅氏逆变换，使随机样本的模拟速度较三角级数法有大幅度的提高。逆傅氏变换法通用性强，数据处理速度快，精度较高，因此本文中运用逆傅氏变换法进行数值模拟，以便快速准确的得到结果，即首先根据轨道高低不平顺功率谱求出高低频谱的幅值和随机相位，而后通过傅里叶逆变换得到轨道高低不平顺的空间域（时域）样本。

已有的轨道不平顺功率谱均是空间域谱，应先将其转化成时域频谱，再在时域功率谱密度函数上离散采样，构造出频谱X（k），然后再对其进行傅立叶逆变换，即可得到模拟不平顺的时域激扰函数x（k）。利用逆傅氏变换法模拟的中国高速铁路无砟轨道高低不平顺时程曲线见图2。

图2 模拟的无砟轨道高低不平顺时程曲线Fig.2 High and low irregularity time curve of ballas tless track

2 CRTSⅢ型板式无砟轨道车辆-轨道垂向耦合振动模型的求解

车辆系统和轨道结构的振动方程不是完全独立的，而是通过轮轨接触力互相耦合的，故运用迭代法对两系统方程分别交叉求解。动力学方程的求解利用Newmark-β数值积分法[5～6]。

起始时间步在车辆初始位置做重力平衡迭代计算后，在后续每一时间步需更新车辆沿轨道运动的位置，各时步首次迭代时，假设轨道结构初始位移为上一时步计算结果，从而利用轮轨接触点的钢轨位移与新位置点的轨面不平顺值，按照Hertz非线性接触公式求得轮轨力，进而将轮轨力代入车辆系统运动方程以计算车辆系统动力响应；利用计算所得轮对位移更新轮轨力，进而代入轨道系统求解轨道结构的动力响应。车体运动时步计算中每一时步中迭代计算以前后两次迭代步求得的轨道系统位移之差满足所定义的收敛容差，则认为收敛性得到满足，而转入下一时步计算，直至所有时步计算完毕。车辆-轨道系统耦合方程的交叉迭代求解流程见图3。

图3 模型求解流程Fig.3 Model solving process

3 模型计算参数与计算结果

利用本文模型仿真计算了CRH3型车辆以300 km/h速度通过CRTSⅢ型板式无砟轨道时车辆-轨道耦合系统的动力响应。车辆-轨道垂向耦合振动模型计算参数见表3。

表3 模型计算参数Tab.3 Model calculation parameters

提取本文模型仿真计算结果的时程曲线，车体加速度时程曲线见图4，垂向轮轨力时程曲线见图5，钢轨及道床板垂向位移时程曲线见图6。

图4 车体加速度时程曲线Fig.4 Time curve of body acceleration

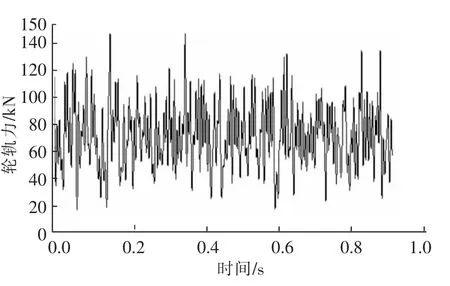
图5 垂向轮轨力时程曲线Fig.5 Time curve of vertical wheel force

钢轨加速度时程曲线见图7、道床板垂向加速度时程曲线见图8。

参数敏感性分析是将其他因素保持在基准值，来考察单项影响因素对主体指标产生的影响。假设车辆-轨道耦合系统动力响应P及它的n个因素，可以表示为P=f（x1，x2，x3，…，xn）。假定一个基准状态P*= f（x1*，x2*，x3*，…，xn*），分别令每单个因素在基准状态上下浮动，计算单一因素的变动对P的影响程度。定义敏感度[9]：

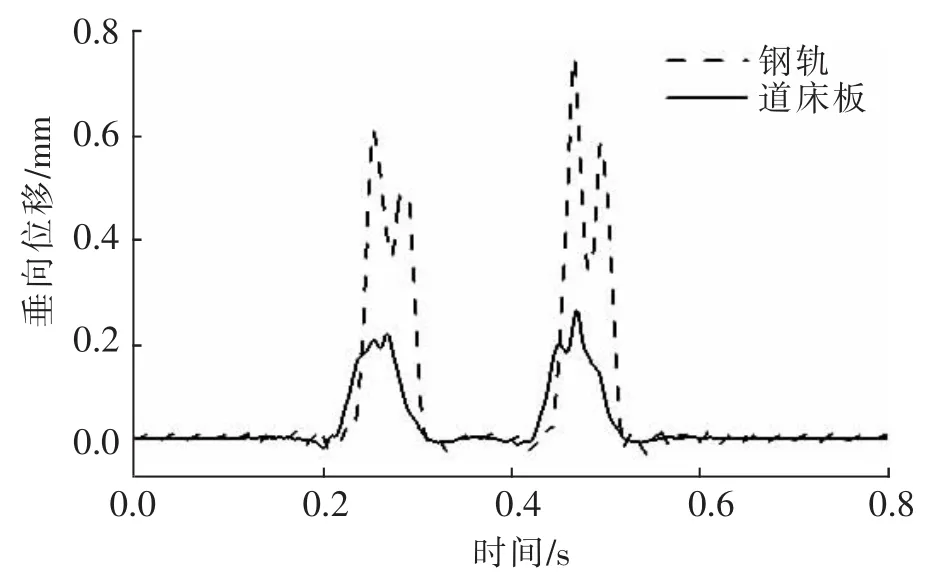
图6 钢轨及道床板垂向位移时程曲线Fig.6 Time curve of rail and track bed vertical displacement

不同于CRTSⅠ型、CRTSⅡ型板式无砟轨道[10]，CRTS III型板式无砟轨道采用自密实混凝土作为填充调整层。为确定CRTS III型板式无砟轨道结构的合理参数，现分析自密实混凝土弹性模量、支承层弹性模量和路基支承刚度对车辆-轨道耦合系统钢轨动位移最大值、轮轨力最大值、车体加速度最大值等动力响应指标的敏感度。采用单因素敏感性分析法，敏感性分析中，计算基准状态自密实混凝土弹性模量、支承层弹性模量和路基支承刚度的取值组合为（20 GPa，25 GPa，90 MN/m），每次在基准状态的基础上只变动自密实混凝土弹性模量、支承层弹性模量其中一个因素，而保持另一因素不变，分析结果见表4与表5。

表4 自密实混凝土弹性模量的敏感度计算Tab.4 Sensitivity calculation of elastic modulus of self-compacting concrete

表5 支承层弹性模量的敏感度计算Tab.5 Sensitivity calculation of elastic modulus of support layer

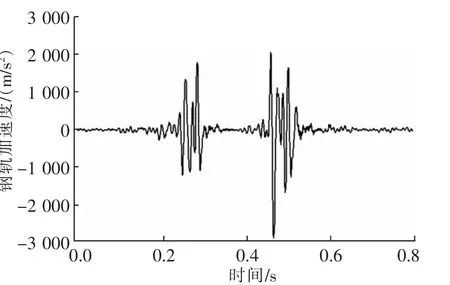
图7 钢轨加速度时程曲线Fig.7 Time curve of rail acceleration

图8 道床板垂向加速度时程曲线Fig.8 Time curve of vertical acceleration of the bed plate

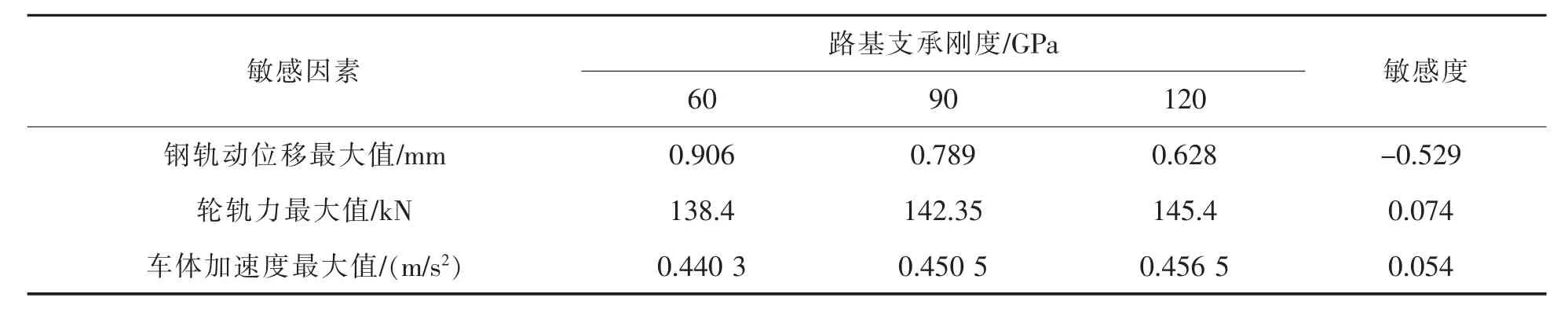
表6 路基支承刚度的敏感度计算Tab.6 Sensitivity calculation of subgrade support stiffness

由表4和表5可知，随着自密实混凝土弹性模量、支承层弹性模量的提高及路基支承刚度的提高，钢轨动位移最大值减小，但轮轨力最大值与车体加速度最大值均增大；自密实混凝土弹性模量比支承层弹性模量对钢轨动位移最大值、轮轨力最大值和车体加速度最大值的影响程度大；但除了钢轨动位移最大值受路基支承刚度与自密实混凝土弹性模量的影响稍大外，且路基支承刚度比自密实混凝土弹性模量对钢轨动位移的影响程度大，而轮轨力最大值与车体加速度最大值对自密实混凝土弹性模量、支承层弹性模量与路基支承刚度的变化不很敏感，尤其是车体加速度最大值的变化不大。

4 结语

根据CRTSⅢ型板式无砟轨道系统结构特点，运用车辆-轨道耦合动力学理论，采用时域动力有限元方法，并引入无限单元法消除边界效应，建立CRTSⅢ型板式无砟轨道车辆-轨道耦合系统垂向动力分析模型，进而利用单因素敏感性分析法分析了结构参数对车辆-轨道系统动力响应指标的敏感度，并得到如下结论：

1）随着自密实混凝土弹性模量、支承层弹性模量的提高及路基支承刚度的提高，钢轨动位移最大值减小，但轮轨力最大值与车体加速度最大值均增大；

2）自密实混凝土弹性模量比支承层弹性模量对钢轨动位移最大值、轮轨力最大值和车体加速度最大值的影响程度大；

3）除了钢轨动位移最大值受自密实混凝土弹性模量的影响稍大外，轮轨力最大值与车体加速度最大值对自密实混凝土弹性模量、支承层弹性模量与路基支承刚度的变化不很敏感，尤其是车体加速度最大值的变化不大。

[1]翟婉明.车辆－轨道耦合动力学[M].3版.北京：科学出版社，2007.

[2]曾庆元，郭向荣.列车桥梁时变系统振动分析理论与应用[M].北京：中国铁道出版社，1999.

[3]翟婉明，韩卫军，蔡成标，等.高速铁路板式轨道动力特性研究[J].铁道学报，1999，21（6）：64-69.

[4]娄平，曾庆元.移动荷载作用下板式轨道的有限元分析[J].交通运输工程学报，2004，4（1）：29-33.

[5]LEI X，MAO L.Dynamic response analyses of vehicle and track coupled system on track transition of conventional high speed railway[J].Journal of Sound and Vibration，2004，271（35）：1133-1146.

[6]雷晓燕，张斌，刘庆杰.轨道过渡段动力特性的有限元分析[J].中国铁道科学，2009，30（5）：15-21.

[7]YANG X，GU S，ZHOU S，et al.Effect of track irregularity on the dynamic response of a slab track under a high-speed train based on the composite track element method[J].Applied Acoustics，2015，99：72-84.

[8]TB/T 3352-2014高速铁路无砟轨道不平顺谱[S].中国铁道出版社，2014.

[9]章光，朱维申.参数敏感性分析与试验方案优化[J].岩土力学，1993（1）：51-58.

[10]李中华.CRTSⅠ型与CRTSⅡ型板式无砟轨道结构特点分析[J].华东交通大学学报，2010，27（1）：22-28.

Sensitivity Analysis of Dynamic Parameters for CRTSⅢSlab Ballastless Track System Based on Finite-infinite Element Method

Li Wei
（China Railway First Survey&Design Institute Group Co.，Ltd.，Xi’an 710043，China）

The CRTS III slab ballastless track is China's self-brand ballastless track with independent intellectual property rights.Focusing on the dynamic parameter determination and optimization problem of CRTS III slab ballastless track system and based on the structure characteristics of CRTS III slab ballastless track system,this study established a vertical vibration analytical model for CRTS III slab ballastless vehicle-track coupling system by applying vehicle-track coupled dynamics theory，time-domain dynamic finite element method and the infinite element method to eliminate boundary effect.Then the MATLAB program was compiled and the sensitivity of structural parameters to the dynamic response of vehicle-track system was analyzed by single factor sensitivity analysis method，which may provide theoretical support for the determination and optimization of dynamic parameters of CRTS III type ballastless track.

high-speed railway；ballastless track；coupled dynamics；finite element；infinite element

U211

A

1005-0523（2017）03-0027-07

（责任编辑 王建华）

2017－03－27

李伟（1982—）男，工程师，研究方向为铁道工程。