流域洪水预报分布式模型参数自动优选*

陈洋波，徐会军，李计

(1. 中山大学地理科学与规划学院，广东 广州 510275； 2.福建省水文水资源勘测局，福建 福州350001)

流域洪水预报分布式模型参数自动优选*

陈洋波1，徐会军2，李计1

(1. 中山大学地理科学与规划学院，广东 广州 510275； 2.福建省水文水资源勘测局，福建 福州350001)

总结归纳了分布式模型参数自动优选的理论，提出了基于粒子群算法的流域洪水预报流溪河模型参数自动优选方法。以武江坪石水文站以上流域为研究对象，构建了流域洪水预报流溪河模型，采用一场实测洪水，优选了模型参数,参数优选进化次数为48次。对13场实测洪水过程进行了模拟，确定性系数平均达89%，相关系数达96%，洪峰误差为2.4%，采用粒子群算法自动优选的流溪河模型参数洪水模拟的效果比采用流溪河模型半自动优选方法得到的参数的模拟效果好。

洪水预报；分布式模型；流溪河模型；参数优选；粒子群算法

分布式物理水文模型(以下简称分布式模型)可以精细化刻画流域下垫面特性，Ambroise等[1]认为分布式模型具有提高流域水文过程模拟和预报精度的潜力。目前国内外已提出了一批分布式模型，代表性的如SHE模型[2]、VIC模型[3]、Vflo模型[4]、LL模型[5]、流溪河模型[6-9]、EasyDHM模型[10-11]等。分布式模型根据流域下垫面特性，如土壤、植被、地形等直接推求模型参数，理论上来说不需要进行模型参数优选。但在实际应用中，目前还缺乏科学的、定量的参数推求方法，主要参数的确定主要依赖于有限的实验室实验数据和当地经验，实际确定的模型参数的不确定性较高。由于分布式模型每个单元采用不同的模型参数，参数是海量的，单元流域上参数不确定性在单元流域上的累积会对模型洪水模拟和预报的精度产生较大，目前的分布式模型在对精度要求较高的应用领域，如洪水预报等的应用受到了限制。如何确定模型分布式模型参数已成为世界性的难题。

采用优化技术对模型参数进行率定，是集总式模型控制模型参数不确定性的普遍措施。由于分布式模型参数众多，对所有模型参数进行优选的计算工作量太大，实际计算无法进行，本文称这一现象为分布式模型的计算灾难。Vieux等[4]提出采用比尺法对Vflo模型参数进行调整，即对模型的所有同类参数，采用一个相同的缩放系数进行同倍比缩放，在一定程度上提高了模型的性能。但由于该方法通过手工的方式操作，实际应用的效果有限。雷晓辉等[10-11]基于这一思路，采用SCE_UA优化技术对EasyDHM模型的一个主成份参数进行了优选，提升了模型在模拟日径流过程时的效果，但优选的模型参数只有一个。徐会军等[12]采用SCE_UA算法对流溪河模型应用于洪水预报时的模型参数进行了优选，明显提高了模型的性能。目前此领域的研究虽然不多，但也表明对分布式模型进行参数优选可以降低模型参数的不确定性。本文的研究目的就是在国内外现有研究工作的基础上，对分布式模型进行参数优选进行系统的总结和归纳，提出分布式模型进行参数优选的理论依据，并提出一种科学可靠的分布式模型进行参数优选方法。

本文首先总结提出了分布式模型参数优选的理论基础，包括参数具有物理意义、参数具有不确定性、参数具有敏感性和参数具有可确定性，这一理论基础适用于所有分布式模型。在些基础上，提出了分布式模型参数优选的框架，并以流溪河模型为例，提出流域洪水预报参数自动优选的改进粒子群算法。华南地区武江流域的研究发现，粒子群算法具有收敛速度快，优化性能好的优点。模型参数优选可大幅度提高流溪河模型流域洪水预报的精度，分布式模型也需要开展模型参数优选。

1 分布式模型参数自动优选理论与方法

1.1 分布式模型参数优选理论基础

对分布式模型参数，本文提出如下的假定，作为分布式模型参数优选的理论基础。

1)分布式模型参数具有物理意义。分布式模型是具有物理意义的模型，不仅其水文过程是有物理意义的，模型参数也是有物理意义的，模型参数的值与并且只与所在单元的一种流域物理特性相关联。

2)分布式模型参数具有不确定性。分布式模型参数可以根据流域物理特性直接确定，模型参数存在着一个理论上的真值。但实际上由于对模型参数确定基础理论及方法理解和掌握的局限性，确定的模型参数值与真值有偏差，这个偏差称为模型参数取值的不确定性，简称为模型参数不确定性。

由于模型参数取值的偏差，模型的计算结果也会相应出现偏差，这种现象称为模型参数不确定性所带来的模型模拟或预报结果的不确定性。

3)分布式模型参数具有敏感性。分布式模型参数对模型计算结果的影响有差异，有些模型参数值的较小变化就会引起模型计算结果较大的变化，而有些模型参数即使其值变化较大，对模型计算结果的影响也不是特别明显，分布式模型参数的这一特征称为参数的敏感性。

4)分布式模型参数具有可确定性。确定分布式模型参数的真值将是十分困难的，但可以确定一个有限接近于真值的分布式模型参数，该参数可以使分布式模型的模拟和预报性能达到实用化的要求。这个模型参数称为模型的最优参数，可将其看成是模型参数的真值，可以通过参数优选方法确定。

1.2 分布式模型参数优选框架

本文提出一个分布式模型参数优选的通用框架，可应用于所有的分布式模型。这个框架有4个步骤，包括参数概化、优选参数取值范围的确定、选择优选方法和性能评估。

1.2.1 参数概化 分布式模型每个单元上均采用不同的模型参数，一个流域可能被划分成上百万个单元，有上千万个参数，对每个单元上的每个参数均进行优选是不现实的，可从分布式模型参数具有物理意义的理论出发，先对模型参数进行概化，再进行参数优选。

将模型参数分成4类，第一类是与气候因素有关的参数，称为气候参数，第二类是与地形有关的参数，称为地形参数，第三类是与土壤类型有关的参数，称为土壤参数，第四类则是与土地利用类型有关的参数，称为土地利用参数。每一类参数与他们相关联的物理属性相关，如土壤参数认为与土壤类型有关，根据土壤的物理特性来确定相应类的模型参数。将物理特性相同的所有单元上的参数作为一个独立的参数，仅对独立参数进行优选，大幅度减少了独立模型参数的数量，使模型参数自动优选计算变得可能。这一参数概化方法可用于目前国内外所有的分布式模型。

1.2.2 参数初值化及取值范围的确定 确定了拟优选的模型参数后，就可以根据流域物理特性数据确定一个模型的初始参数，现有的国内外主要的分布式模型均提出了相应的参数初值确定方法，可据此确定模型参数初始。在此基础上，确定模型参数的取值范围。由于目前国内外对分布式模型研究与应用的经验有限，模型参数的取值范围还没有一个可有效借鉴的值，本文提出先对参数进行归一化处理，即对各参数进行如下处理：

(1)

1.2.3 选择优选方法 确定了模型参数的初值及取值范围后，就要选择适当的优选方法进行模型参数的自动优选，文中基于粒子群算法进行流溪河模型的参数自动优化研究。目前国内外提出了大量的优选方法，在集总式模型参数自动优选中采用较多的方法有自适应随机搜索算法[13]，模拟退火算法[14]，遗传算法[15]，SCE-UA算法[16]，蚁群算法[17]，粒子群算法[18]等。在分布式模型参数优选中，只有SCE-UA法被使用过。不同的分布式模型，可选用不同的优选算法，本文提出的方法不规定具体的优化算法。

1.2.4 性能评估 模型参数优选后，还需要对算法的性能和模型的性能进行评估，以确定参数优选是否有效。算法性能评估主要检查算法是否收敛，收敛速度的快慢，以确定该优化算法是否适用于该模型。模型的性能评估可统计模拟的洪水过程的评价指标，一般可包括确定性系数、过程相对误差、洪峰相对误差、水量平衡系数等。不同的模型也可选择其中的部分指标进行评价。

1.3 基于粒子群算法的流溪河模型参数自动优选方法

本文针对流溪河模型，提出一个基于粒子群算法的参数自动优选方法。流溪河模型是一个主要用于流域洪水预报的分布式物理水文模型。流溪河模型每个单元上共有13个参数，按照上述的方法分成4种类型，包括气象类参数、地型类参数、土壤类参数和植被类参数。气象类参数为潜在蒸发率，地型类参数为流向和坡度，植被类参数为蒸发系数和边坡单元糙率，土壤类型参数为土壤层厚度、土壤特性系数(b)、饱和含水率、田间持水率、凋萎含水率和饱和水力传导率。流向和坡度由DEM计算确定，不再调整，又称为不可调参数。其它参数则在初始值的基础上，采用本文提出的分布式模型参数优选方法进行优选，优选算法选择改进粒子群算法(以下简称PSO法)。

PSO法是由美国心理学家James Kennedy和电气工程师Russell Eberhart于1995年[18]在模拟鸟群捕食觅食过程中的迁徙和群集的社会行为时提出的一种与进化计算有关的群体智能随机优化策略。PSO是一种全局群体寻优算法，通过群体中粒子之间的合作、竞争机制，智能地指导群体的优化搜索过程，每个粒子都具有“自我经验总结”和“群体共享”的双重特点，其理论基础是通过个体间的协作与竞争，实现复杂空间中最优解的搜索。

PSO算法思路为：算法中的每个粒子代表一个参数解集，粒子通过记忆、追随个体最优及群体最优的位置来更改自身的速度与方向，实现寻优过程。通过以下公式实现粒子的速度变换及位置变换。

(2)

(3)

式中，Vi,k，第i个粒子k时刻运行速度；Xi,k，第i粒子k时刻位置；Xi,pBest，第i粒子个体最优位置；XgBest，粒子全局最优位置；ω惯性加速度；C1，C2，学习因子。

采用PSO法进行流溪河模型参数优选的计算步骤归纳如下：① 粒子群参数设置：设置粒子个数P，确定粒子维数N，即优选择的参数个数，惯性因子ω和学习因子C1、C2的取值范围；② 粒子群初始化：在参数空间中随机生成P个粒子；③ 开始循环寻优计算，首先计算每个粒子的适应度值，即目标函数值，再计算粒子局部最优值pBest和全局最优值gBest；④ 按照公式(2)和(3)更新每个粒子的速度V，位置X；⑤ 终止循环寻优：根据收敛条件，判断是否满足终止条件，输出最优值；否则返回步骤③，直到达到终止条件。

在初期的PSO算法中，惯性因子ω和学习因子C1、C2取固定值，后来的研究发现，动态调整ω、C1和C2的值，可以改进算法的性能[19-20]，基于这一算法的PSO称为改进PSO，本文采用改进PSO法进行流溪河模型参数优选。对ω，本文采用由Eberhart & Shi[18]提出的LDIW(linearly decreasing inertia weight strategy)法进行动态调整，计算公式如下：

(4)

其中，i为当前进化次数，MaxN为最大进化次数，ωmax和ωmin分别为惯性因子ω取得的最大和最小值，分别取为0.9和0.1。

C1和C2的取值则采用由Chen等[21]提出的反余弦函数策略(arccosine function strategy)来调整，计算公式如下。

(5)

(6)

2 研究案例与数据

2.1 研究流域

武江是华南地区广东省境内最大的流域北江流域上游的一级支流，流域面积7 097 km2。流域内暴雨洪水多发，历史上多次发生大洪水，平均每2 a发生一次较大洪水，每4 a发生一次大洪水，是广东省重点防洪流域。本文以武江坪石水文站以上的流域部分为研究对象，称为武江中上游流域。坪石水文站位于广东省乐昌市坪石镇中心区域上游，控制流域面积3 622 km2。图1为武江中上游流域的行政区划和雨量站分布图。

武江中上游流域内有17个雨量站，流域出口处的坪石水文站有可靠的洪水观测资料，本项目研究中收集整理了14场实测洪水过程资料，包括坪石水文站的流量及各雨量站的降雨。

2.2 建模数据收集

流溪河模型建模所需的流域物理特性数据包括DEM、土地利用类型和土壤类型。本次研究采用的DEM数据来自于美国航天飞机雷达地形测绘计划公共数据库免费的DEM数据，空间分辨率为90 m×90 m，如图2(a)。土地利用类型数据采自于美国地质调查局(USGS)30″×30″全球土地覆盖数据库，空间分辨率为1 000m×1 000m，经过重采样处理得到空间分辨率为90m×90m的土地利用类型，如图2 (b)，主要类型有9种，包括常绿针叶林、常绿阔叶林、矮树丛、稀树林、海滨湿地、高山和亚高山草甸、平原草原、湖泊和沼泽地，各类型的覆盖率分别为0.3%、9.5%、3.7%、73.1%、0.2%、2.0%、0.3%、6.5%、4.5%。土壤类型数据取自于国际粮农组织(FAO) 于2008年发布的30m×30m中国土壤分布数据库，空间分辨率为1 000m×1 000m，经过重采样获得空间分辨率为90m×90m的土壤类型数据，如图2 (c)，共有12种类型，包括水体、腐殖质强淋溶土、艳色高活性强酸土、铁铝始成土、弱发育淋溶土、不饱和始成土、石灰性粗骨土、不饱和粗骨土、弱发育高活性强酸土、堆积人为土、黑色石灰薄层土和不饱和薄层土，各类型所占流域面积的比例分别为4.8%、56.5%、0.5%、3.4%、6.5%、4.5%、0.7%、5.6%、9.8%、6.6%、1.0%、0.2%。

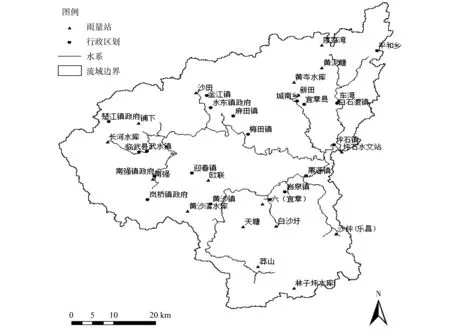
图1 武江中上游流域简图Fig.1 The scheme map of the upper and middle Wujiang River Basin

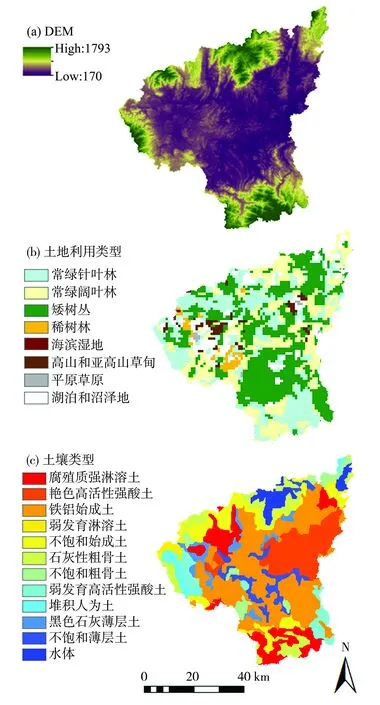
图2 武江中上游流域物理特性数据Fig.2 The physical characteristics data of the upper and middle basin of Wujiang River

3 流溪河模型构建

3.1 流溪河模型构建

构建流溪河模型就是以DEM为依据，对流域进行单元划分，构建汇流网络，对单元进行分类，在此基础上，对河道断面尺寸进行估算。采用空间分辨率为90m×90m的DEM对流域进行划分，按照流溪河模型中的单元分类方法对单元进行分类，将单元分成了个河道单元和边坡单元。由于流域内没有调蓄能力强的水库，故未划分水库单元。河道划分为3级河网，参照GoogleEarth遥感影像，设置了河道结点，将河道分成了虚拟河段，并估算了各个虚拟河道的断面宽度、侧坡及底坡。单元分类及河道虚拟结点和虚拟河段的划分结果如图 3。

3.2 模型初始参数推求

土地利用类型参数是边坡糙率(n)和蒸发系数(v)。蒸发系数v是个非常不敏感的参数，根据文献[22]的推荐值取为0.7，土地利用参数初值选取情况如表 1。

流溪河模型土壤类型参数中的土壤特性(b)一般推荐值为2.5。饱和含水率、田间持水率和饱和水力传导率，本文采用由Arya等[23]提出的土壤水力特性计算器来进行计算，确定的武江中上游流域土壤类型参数初值如表 2。

图3 模型结构示意图Fig.3 Schematic diagram of model structure

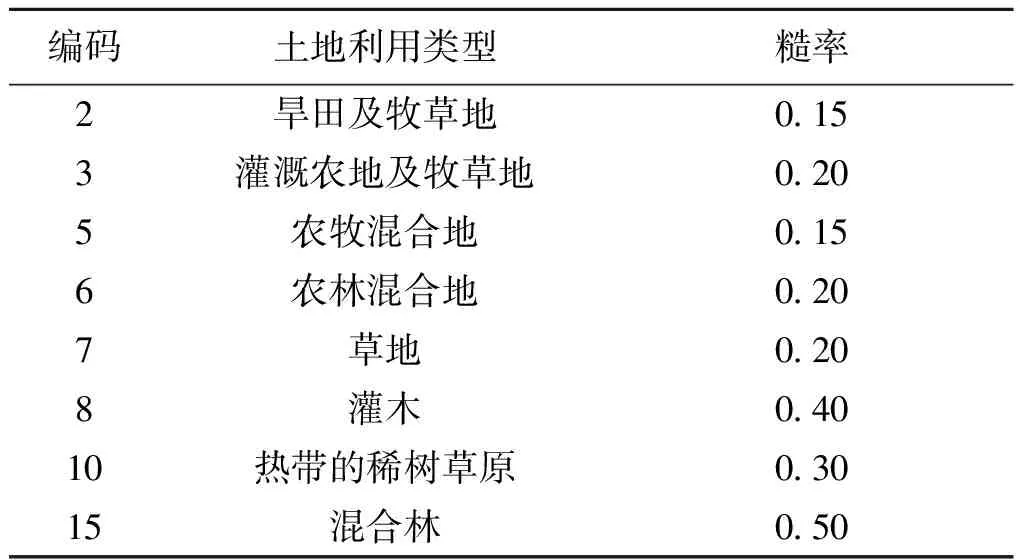
编码土地利用类型糙率2旱田及牧草地0153灌溉农地及牧草地0205农牧混合地0156农林混合地0207草地0208灌木04010热带的稀树草原03015混合林050

4 结果与讨论

4.1 可调参数自动优选

采用PSO法对武江中上游流域流溪河模型12个可调参数进行自动优选。从收集的14场洪水中选择flood1985052618号洪水过程进行参数自动优选，图4列出了参数优选计算过程中的部分结果。

图4(a)为参数优选过程中目标函数值的进化过程，图4(b)为参数的进化过程。从图中可以看出，随着寻优进程的推进，当进化计算次数达到28次时，目标函数值趋近于稳定，当进化计算次数达到48次时，模型参数值收敛到最优值，这说明PSO法具有较好的收敛速度。表 3列出了参数优选结果。

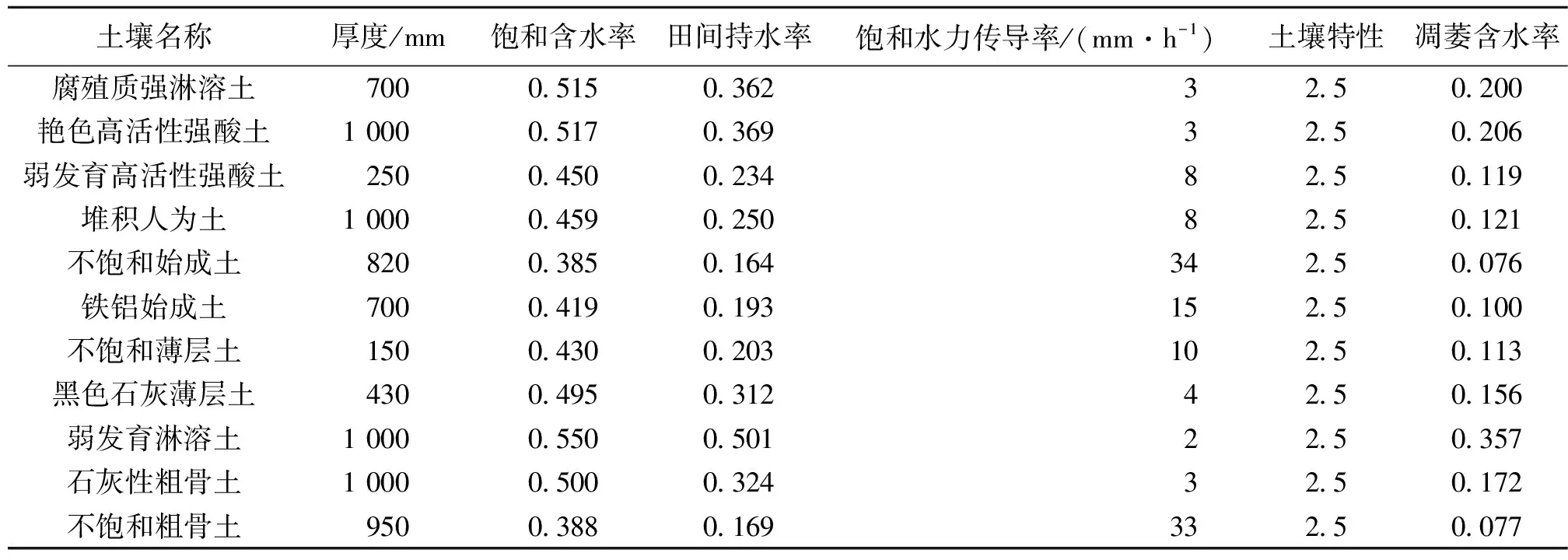
表2 武江中上游流域土壤类型参数初值

图4 参数优选过程图Fig.4 The procedure chart of parameter optimization

统计该场洪水模拟效果的评价指标，确定性系数为0.936，相关系数为0.979，水量平衡系数为0.98，过程相对误差为16%，洪峰相对误差为1.4%，峰现时间差为-3h，洪水模拟的效果优良。

4.2 参数优选效果分析

采用上述优选的模型参数，对其它13场洪水进行了模拟，统计了6个评价指标，如表 4所示。

从表4的6个评价指标可见，13场洪水模拟的确定性系数均值达89%，相关系数达96%，洪峰误差均值为2.5%，平均峰现时间提前了2h。表明采用粒子群算法优选的流溪河模型参数具有较优的性能，可以用来进行武江中上游流域的洪水预报。

表3 武江中上游流域流溪河模型参数优选结果

流溪河模型目前主要采用半自动化的参数优选方法开展模型参数调整，为了比较粒子群算法参数自动优选与半自动参数优选的效果，本文采用同一场洪水—flood1985052618号洪水，应用半自动化的参数优选方法对武江中上游流域流溪河模型参数进行了调整，得到了模型参数如表 5。

统计该场洪水模拟效果的评价指标，确定性系数为0.735，相关系数为0.874，水量平衡系数为0.9，过程相对误差为27%，洪峰相对误差为2.4%，峰现时间差为-4h，洪水模拟的效果尚可。但与粒子群算法优选的参数的模型模拟效果对比，其洪水过程模拟的整体效果不如基于粒子群算法优选的参数的模型模拟的效果。

采用该组参数(表 5)对其余13场洪水进行了模拟，各场洪水模拟的评价指标统计结果如表 6。 进而将表6各统计指标值的平均值与表5进行对比，结果如表 7。

从表7中2种参数优选方法统计指标对比结果可知，基于PSO算法优选的参数的模型的模拟效果优于半自动化算法确定的参数的模型的模拟效果，6个评价指标均有所提高。对两种不同参数的模型模拟的洪水过程进行了对比分析，图5给出了其中6场洪水的对比结果。

从图5的模拟结果来看，采用粒子群算法优选的参数的模型的模拟效果明显优于采用半自动化方法优选的参数的模型的模拟效果，说明采用粒子群算法自动优选流溪河模型参数可提高模型洪水预报的性能。

表4 流溪河模型验证结果表

表5 武江中上游流域流溪河模型半自动化参数优选结果

表6 参数半自动优选流溪河模型验证结果表

表7 粒子群算法和半自动化参数优选方法洪水模拟统计指标对比

图5 洪水过程模拟结果对比图Fig.5 Hydrological process comparison simulated with two different parameter sets

5 结 论

本文总结归纳了分布式模型参数自动优选的理论，提出了基于粒子群算法的流域洪水预报流溪河模型参数自动优选方法，该方法也可以用于国内外主要的分布式物理水文模型。以武江坪石水文站以上流域为研究对象，构建了流域洪水预报流溪河模型，采用一场实测洪水，优选了模型参数；对13场实测洪水过程进行了模拟，确定性系数平均达89%，相关系数达96%，洪峰误差为2.4%，平均峰现时间提前2h，模拟效果优良。采用粒子群算法自动优选研究流域流溪河模型参数时，仅经过48次优选计算就获取了最优参数。采用粒子群算法自动优选的流溪河模型参数洪水模拟的效果比采用流溪河模型半自动优选方法得到的参数的模拟效果好。采用粒子群算法自动优选流溪河模型参数优化性能好，计算效率高，收敛性能好。

[1]AMBROISEB,BEVENK,FREERJ.TowardageneralizationoftheTOPMODELconcepts:Topographicindicesofhydrologicsimilarity[J].WaterResourRes, 1996,32:2135-2145.

[2]ABBOTTMB,BATHURSTJC,CUNGEJA,etal.AnintroductiontotheEuropeanhydrologicsystem-SystemHydrologueEuropeen,“SHE”,2:Structureofaphysicallybased,distributedmodelingsystem[J].JournalofHydrology, 1986,87(1/2):61-77.

[3]LIANGX,LETTENMAIERDP,WOODEF,etal.Asimplehydrologicallybasedmodeloflandsurfacewaterandenergyfluxesforgeneralcirculationmodels[J].JournalofGeophysicalResearchAtmospheres, 1994, 99(D7):14415-14428.

[4]VIEUX,BE,VIEUXJE.VfloTM:Areal-timedistributedhydrologicmodel[C]∥Proceedingsofthe2ndFederalInteragencyHydrologicModelingConference.Nevada,2002.

[5] 李兰, 钟名军. 基于GIS的LL-Ⅱ分布式降雨径流模型的结构[J]. 水电能源科学, 2003(4):35-38.LIL,ZHONGMJ.StructureoftheLL-Ⅱdistributedrainfall-runoffmodelbasedonGIS[J].WaterResourcesandPower, 2003(4):35-38.

[6] 陈洋波.流溪河模型[M].北京:科学出版社,2009:198.

[7] 陈洋波,任启伟,徐会军,等.流溪河模型I:原理与方法[J]. 中山大学学报(自然科学版), 2010, 49(1):107-112.CHENYB,RENQW,XUHJ,etal.LiuxihemodelⅠ:principleandmethod[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2010, 49(1):107-112.

[8] 陈洋波,黄锋华,徐会军,等.流溪河模型Ⅱ:参数推求[J]. 中山大学学报(自然科学版), 2010, 49(2):105-112.CHENYB,RENQW,XUHJ,etal.LiuxihemodelⅡ:parametercalibration[J].ActaScientiarumNaturaliumUniversitatisSunyatseni,2010,49(2):105-112.

[9]CHENYB,RENQW,HUANGFH,etal.Liuxihemodelanditsmodelingtoriverbasinflood[J].JournalofHydrologicEngineering,2011,16(1): 33-50.

[10] 雷晓辉, 廖卫红, 蒋云钟,等. 分布式水文模型EasyDHM(Ⅰ):理论方法[M]. 北京:中国水利水电出版社, 2010.

[11] 雷晓辉, 蒋云钟, 王浩,等. 分布式水文模型EasyDHM(Ⅱ):应用实例[J]. 水利学报, 2010, 41(8):893-899.LEIXH,JIANGYZ,WANGH,etal.DistributedhydrologicalmodelEasyDHM(Ⅱ):Application[J].ShuiLiXueBao, 2010, 41(8):893-899.

[12] 徐会军, 陈洋波, 曾碧球,等.SCE-UA算法在流溪河模型参数优选中的应用[J]. 热带地理, 2012, 32(1):32-37.XUHJ,CHENYB,ZENGBQ,etal.ApplicationofSCE-UAalgorithmtoparameteroptimizationofLiuxihemodel[J].TropicalGeography,2012, 32(1):32-37.

[13]MASRISF,BEKEYGA,SAFFORDFB.Aglobaloptimizationalgorithmusingadaptiverandomsearch[J].AppliedMathematicsandComputation,1980,7(4):353-375.

[14]KIRKPATRICKS,GELATTCD,VECCHIMP.Optimizationbysimulatedannealing[J].Science,1983,220(4598):671-680.

[15]GOLDBERGDE.Geneticalgorithmsinsearch,optimizationandmachinelearning[M].NewJersey:Addison-Wesley,1989:120.

[16]DUANQ,SOROOSHIANS,GUPTAVK.OptimaluseoftheSCE-UAglobaloptimizationmethodforcalibratingwatershedmodels[J].JournalofHydrology,1994,158(3/4):265-284.

[17]DORIGOM,MANIEZZOV,COLORNIA.Antsystem:optimizationbyacolonyofcooperatingagents[J].IEEETransactionsonSystems,Man&Cybernetics:partB(Cybernetics), 1996, 26(26):29-41.

[18]SHIY,EBERHARTRC.Particleswarmoptimization:developments,applicationsandresources[C]∥Proceedingsofthe2001congressonevolutionarycomputation.IEEE, 2001.

[19]GOHARYEA,RUZAIZAAS.Chaosandadaptivecontrolintwoprey,onepredatorsystemwithnonlinearfeedback[J].Chaos,Solitons&Fractals, 2007,34:443-453.

[20]CHUANGLY,HSIAOCJ,YANGCH.Chaoticparticleswarmoptimizationfordataclustering[J].ExpertSystAppl,2011,38:14555-14563.

[21] 陈水利, 蔡国榕, 郭文忠,等.PSO算法加速因子的非线性策略研究[J]. 长江大学学报(自然科学版), 2007, 4(4):1-4.CHENSL,CAIGR,GUOWZ,etal.Studyonthenonlinearstrategyofaccelerationcoefficientinparticleswarmoptimization(PSO)algorithm[J].JournalofYangtzeUniversity(NatSciEdit), 2007, 4(4):1-4.

[22]WANGZM,BATELAANO,SMEDEFD.Adistributedmodelforwaterandenergytransferbetweensoil,plantsandatmosphere(WetSpa)[J].Physics&ChemistryoftheEarth, 1996, 21(3):189-193.

[23]ARYALM,PARISJF.Aphysicoempiricalmodeltopredictthesoilmoisturecharacteristicfromparticle-sizedistributionandbulkdensity[J].SoilScienceSocietyofAmericaJournal, 1981, 45(6):1023-1030.

Automated parameter optimization of distributed hydrological model for watershed flood forecasting

CHENYangbo1,XUHuijun2,LIJi1

(1. School of Geography and Planning, Sun Yat-sen University, Guangzhou 510275, China; 2. Bureau of Hydrology and Water Resources of Fujian Province, Fuzhou 350001, China)

The theory of automatic parameter optimization of the distributed hydrological model, including parameter’s physical meaning, uncertainty, sensitivity and determinability, is presented in this paper. An automatic parameter optimization method based on Particle Swarm Optimization is proposed for the Liuxihe Model in watershed flood forecasting. This method is validated in the Wujiang Catchment in southern China and shows the advantages of high optimal performance, high computational efficiency, and good convergence. The Liuxihe Model based on the automatic parameter optimization method is more efficient.

flood forecasting; distributed hydrological model; Liuxihe model; parameter optimization; Particle Swarm Optimization

10.13471/j.cnki.acta.snus.2017.03.018

2016-04-26 基金项目：国家自然科学基金(50479033)；广东省科技计划项目(2013B020200007)；江西省水利科技项目(KT201407)；水利部公益性行业科研专项基金(201301070)

陈洋波(1964 年生)，男；研究方向：洪水预报，水文模型，水利信息技术;E-mail:eescyb@mail.sysu.edu.cn

TV124

A

0529-6579(2017)03-0125-09