单位球面中具有常平均曲率超曲面的拼挤定理*
王芬,吴雪玲
(1. 湖北第二师范学院数学与经济学院,湖北 武汉 430205; 2. 华中师范大学数学与统计学学院,湖北 武汉 430079)
单位球面中具有常平均曲率超曲面的拼挤定理*
王芬1,吴雪玲2
(1. 湖北第二师范学院数学与经济学院,湖北 武汉 430205; 2. 华中师范大学数学与统计学学院,湖北 武汉 430079)
研究单位球面中具有常平均曲率的超曲面。分别在假设或不假设第二基本形式的长度的平方为常数的情形下,证明了两个重要的拼挤定理。这些结论是Cheng (1996年)和Xu等(2011年)相应结果的推广。
常平均曲率;Clifford环面;陈省身猜想;第二基本形式
单位球面中的具有常平均曲率的超曲面是子流形几何中的重要研究对象,1968年著名数学家陈省身就提出了下面的著名猜想:
令S是具有常数量曲率的n+1维单位球面上的n维闭极小超曲面的第二基本形式的长度的平方,那么S的所有可能取值构成的集合是离散的。
下面,我们先介绍一下该猜想目前的研究状况。
n=3:经过Peng等[1],Chang[2]等的努力,最终被Chang[2]完全解决。具体来讲,我们有
定理1S4中的一个具有常数量曲率的闭极小浸入超曲面是四维球面中的一个赤道,或Clifford极小超曲面,或者Cartan极小超曲面。特别地,S只可能是0,3或6。
去掉“闭”这个条件,我们有下面未解决的问题:
Bryant猜想S4内的具有常数量曲率的极小浸入超曲面是等参的。
n=4:Lusala等[3]证明了S5内的具有非负常数量曲率的闭Willmore极小超曲面M4一定是等参的。
n≥5:未解决。

开问题 设Mn是单位球面Sn+1上的一个n维闭极小超曲面,并且S为常数。如果S>n,那么S>2n?
如果考虑更一般的常平均曲率超曲面,Almeida等[9]和Chang[10]证明了S4中的具有常平均曲率和常数量曲率的闭超曲面M3是等参的。Almeida等[11]证明了:令H,K和R分别表示M3的平均曲率,高斯曲率和数量曲率,如果这三个函数中的两个是常数,那么M3是等参超曲面或者H=K≡0。如果我们不假定Mn具有常数量曲率,Peng等[12](n≤5),Wei等[13](n≤7),Zhang[14](n≤8),Ding等[15](n≥3)证明了如下拼挤定理:
定理2 设M是浸入在Sn+1内的一个极小闭超曲面,(n≥3),并且S是M的第二基本形式的平方形式。 那么存在δ(n)=n/23>0,使得如果n≤S(x) 该结果被Xu等[16]推广到了常平均曲率的情形。关于陈省身猜想更多详细的介绍,请参考文献[17]。 本文主要受Xu等[16]的启发,在一定条件下,得到了拼挤常数的显示表达。具体来讲,我们证明了如下拼挤定理: 则存在仅依赖于n的充分小的正数ε(n)和仅依赖于常数n和H的正数δ(n,H),使得当 时,其中 若S为常数,则有下面的拼挤定理: 定理4Mn是Sn+1中具有常平均曲率H的n维闭超曲面,Mn第二基本形式长度的平方S是常数。如果 nH2f4-2HSf3+S(S-n) 则存在仅依赖于n的充分小的正数ε(n)和仅依赖于常数n和H的正数δ(n,H),使得当 时,其中 注1当H=0时,定理3和定理4就分别为文[18]和文[19]中的主要结果。 在本节中,我们将回顾一些关于Sn+1上的常平均曲率闭超曲面的基本而又重要的等式,这些在文[20]中有更详细的介绍。假定Mn是Sn+1上的一个具有常平均曲率H的n维闭超曲面,那么可以选取一个正交向量场{e1,e2,…,en+1}使得{e1,e2,…,en}切于Mn。令hij和H分别表示M的第二基本形式和平均曲率,则 我们再定义 令hijk和hijkl分别表示第二基本形式的第一、第二协变导数的分量,定义A,B如下 通过计算,可以得到如下相关等式: (1) (2) (3) (4) 引理1[21]设Mn是Sn+1中具有常平均曲率H的n维闭超曲面,则有 n2H2+2nHf3)+ n3H2+2n(n-S)Hf3] 定理3的证明 由式(1)-式(3),通过直接计算,可得 (5) (6) (7) (8) 结合引理1及式(8),可得 S(S-n)-n2H2+2nHf3)+ n3H2+2n(n-S)Hf3] (9) nHSf3-n|▽h|2]≥0 即 (10) (11) 因为 (12) 结合等式(11)及不等式(12),得 (13) 由式(7),通过计算,可得 ∫MnH2f4-2HSf3+nHf3= 代入不等式(13)中,可得 (14) 结合式(10)及式(14),化简可得 S(n2H2+S(S-n)-nHf3)≥0 (15) 又知 结合式(15),整理可得 (n2H2+S(S-n)-nHf3)≥0 (16) 其中 式(16)即 (n2H2+S(S-n)-nHf3)≥0 (17) 因S≥S0,由计算不难得到-S(n-S)+n2H2-nHf3≥0。如果S0≤S≤S0+δ(n,H),δ(n,H)是仅依赖于常数n和H的正数,则 (n2H2+S(S-n)-nHf3) 从而,可以得到 (n2H2+S(S-n)-nHf3)- (18) 即 (n2H2+S(S-n)-nHf3)+ (19) 解不等式,可得 因S0≤S≤S0+δ(n,H),则 因t>0,则 所以 有-S(n-S)+n2H2-nHf3=0,这也就意味着S=S0,M是一个Clifford超曲面。 推论1的证明 当Mn有两个不同主曲率时,满足 再由定理3,可得推论1成立。 定理4的证明 已知S为常数,则 将等式代入式(15)中,可得 化简可得 (20) 则需满足 记Δ=9n2(n+2)4H2+8n(n2+4n+6)(n2+4n+3),易知t>0,则有 所以 记 则 -S(n-S)+n2H2-nHf3=0 有-S(n-S)+n2H2-nHf3=0,意味着S=S0,M一个Clifford超曲面。 推论2的证明 当Mn有两个不同主曲率时,满足 因此由定理4知推论2成立。 [1]PENGCK,TERNGCL.Seminaronminimalsubmanifolds[M].Princeton:PrincetonUnivPress, 1983: 177-198. [2]CHANGSP.OnminimalhypersurfaceswithconstantscalarcurvaturesinS4[J].JDiffGeom, 1993, 37(3): 523-534. [3]LUSALAT,SCHERFNERM,DESOUSAJrLAM.ClosedminimalWillimorehypersurfacesofS5(1)withconstantscalarcurvature[J].AsianJMath, 2005, 9(1): 65-78. [4]SIMONSJ.MinimalvarietiesinRiemannianmanifolds[J].AnnMath, 1968, 88(1): 62-105. [5]YANGHC,CHENGQM.Anoteonthepinchingconstantofminimalhypersurfaceswithconstantscalarcurvatureintheunitsphere[J].ChineseScienceBull, 1991, 36(1): 1-6. [6]YANGHC,CHENGQM.Anestimateofthepinchingconstantofminimalhypersurfaceswithconstantscalarcurvatureintheunitsphere[J].ManuscriptaMath, 1994, 84(1): 89-100. [7]YANGHC,CHENGQM.Chern’sconjectureonminimalhypersurfaces[J].MathZ, 1998, 227(3): 377-390. [8]SUHYJ,YANGHY.Thescalarcurvatureofminimalhypersurfacesinaunitsphere[J].CommunContempMath, 2007, 9(2): 183-200. [9]deALMEIDASEBASTIAOC,BRITOFABIANOGB.Closed3-dimensionalhypersurfaceswithconstantwithconstantmeancurvatureandconstantscalarcurvature[J].DukeMathJ, 1990, 61(1): 195-206. [10]CHANGSP.AclosedhypersurfacewithconstantscalarcurvatureandconstantmeancurvatureinS4isisoparametric[J].CommAnalGeom,1993, 1(1): 71-100. [11]deALMEIDASEBASTIAOC,BRITOFABIANOGB,deSOUSAJrLAM.ClosedhypersurfacesofS4withtwoconstantcurvaturefunctions[J].ResultsinMath, 2007, 50(1):17-26. [12]PENGCK,TERNGCL.Thescalarcurvatureofminimalhypersurfacesinspheres[J].MathAnn, 1983, 266(1): 105-113. [13]WEISM,XUHW.Scalarcurvatureofminimalhypersurfacesinasphere[J].MathResLett, 2007, 14(3): 423-432. [14]ZHANGQ.Thepinchingconstantofminimalhypersurfacesintheunitspheres[J].ProcAmerMathSoc, 2010, 138(5): 1833-1841. [15]DINGQ,XINYL.OnChern’sproblemforrigidityofminimalhypersurfacesinthespheres[J].AdvMath, 2011, 227(1): 131-145. [16]XUHW,XUZY.AnewcharacterizationoftheCliffordtorusviascalarcurvaturepinching[J].JFunctAnal, 2014, 267(10): 3931-3962. [17]SCHERFNERM,WEISSS.TowardsaproofoftheChernconjectureforisoparametrichypersurfacesinspheres[C]∥Proc33SouthGermanDiffGeomColloq, 2008: 1-33. [19]XUYW,XUZY.OnrigidityofCliffordtorusinaunitsphere[J].ApplMathJChineseUniv(SerB), 2011, 26(1): 121-126. [20]CHENGQM,HEYJ,LIHZ.Scalarcurvatureofhypersurfaceswithconstantmeancurvatureinasphere[J].GlasgMathJ, 2009, 51(2): 413-423. [21]DENGQT,GUHL,SUYH.Constantmeancurvaturehypersurfacesinspheres[J].GlasgMathJ, 2012, 54(1): 77-86. The pinched theorems of hypersurfaces with constant mean curvature in unit spheres WANGFen1,WUXueling2 (1. School of Mathematics and Economics, Hubei University of Education, Wuhan 430205, China; 2. School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China) The constant mean curvature hypersurfaces in unit sphereSn+1areconsidered.Underthehypothesisthatthesecondfundamentalformisconstantornot,twoimportantpinchedtheorems,whichgeneralizedcorrespondingresultsofCheng(1996)andXuetal(2011),areobtained. constant mean curvature; Clifford torus; Chern’s conjecture; the second fundamental form 10.13471/j.cnki.acta.snus.2017.03.011 2016-12-16 基金项目:国家自然科学基金(10901067) 王芬(1980年生),女;研究方向:应用数学;E-mail: 55421810@qq.com O186 A 0529-6579(2017)03-0071-071 主要结果
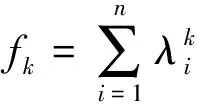

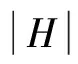
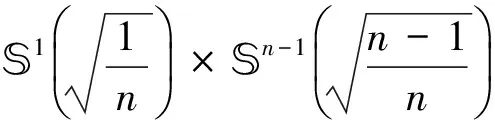

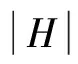

2 预备知识
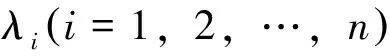
3 定理证明
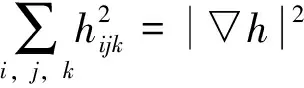
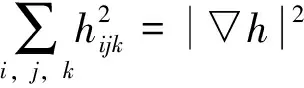
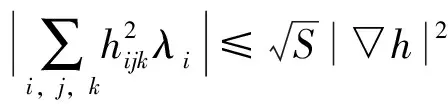
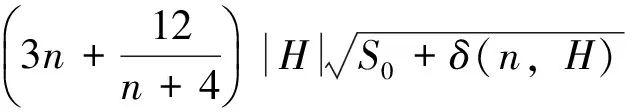
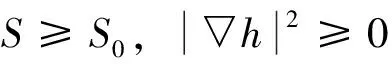





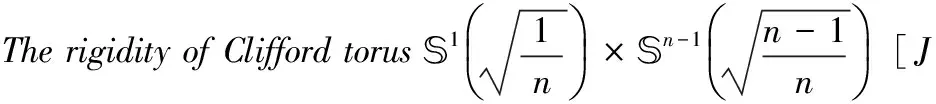
- 中山大学学报(自然科学版)(中英文)的其它文章
- 海底NGH水力提升法最小提升速度和压力损失*
- 流域洪水预报分布式模型参数自动优选*
- Notch1 activation protects against triptolide-induced oxidative damage and apoptosis in hepatocytes*
- 阳江红树林内生真菌Aspergillus sp. 5Y次级代谢产物及其活性的研究*
- 化学水浴法制备ZnS薄膜的结构与性能*
- Existenceofweightedpseudoanti-periodicsolutionstosomeneutraldifferentialequationswithpiecewiseconstantargument*

