海底NGH水力提升法最小提升速度和压力损失*

陈浩，付来强，吕斌，吴文科，黄俊铭

(西南石油大学机电工程学院，四川 成都 610500)

海底NGH水力提升法最小提升速度和压力损失*

陈浩，付来强，吕斌，吴文科，黄俊铭

(西南石油大学机电工程学院，四川 成都 610500)

根据天然气水合物的相关性质，对比总结了现阶段天然气水合物的几种主流开采方法；在现有的天然气水合物水力提升工艺的理论基础上，研究了天然气水合物水力提升系统中天然气水合物颗粒的最小提升速度；采用主流颗粒水力提升最小速度计算理论，并结合天然气水合物颗粒性质计算出天然气水合物颗粒最小提升速度，同时进行了对比；对水力提升系统的管路输送系统进行了理论建模，研究对比得到了天然气水合物输送过程中管路系统中颗粒浓度、颗粒直径、提升速度对天然气水合物提升管路系统中压降的影响。

天然气水合物；水力提升；最小提升速度；提升压损

天然气水合物(Nature gas hydrates,NGH)又名可燃冰，是一种结构和形状类似于冰的物质，一般是由天然气和水在温度低于10 ℃，压力高于10 MPa的环境下生成的[1]。天然气水合物在陆地冻土层，海洋与大陆连接处以及深海中都有广泛分布。因天然气水合物的地理分布情况及其自身的不稳定状态，其开采过程较为困难，因此对天然气水合物开采进行工业化研究变得十分重要。

天然气水合物的开采方法有很多种，主要方法包括[2-8]：降压法、加热法、置换法、注抑制剂法以及水力提升法。而水力提升法相对于其他方法具有开采量大、稳定性强、操作简单等优点。本文首先研究了天然气水合物的开采方法和特点，并基于现有的天然气水合物水力提升工艺基础，研究了提升系统中的水合物颗粒最小提升速度；其次采用主流颗粒水力提升最小速度理论，结合天然气水合物颗粒的性质计算了天然气水合物颗粒最小提升速度，并将两者进行了对比；最后针对水力提升系统中的管路输送系统进行理论建模，并研究颗粒浓度、颗粒直径、提升速度对天然气水合物提升系统压降的影响。

1 天然气水合物水力提升法

2006年，唐良广等[8]基于海洋渗漏型天然气水合物藏而提出的一种非常具有针对性的开采模式，即水力提升法。水力提升法的基本过程为三个步骤：① 利用海底的采矿机器人将天然气水合物进行采集、集中，进行破碎、分离、过滤等初步处理。其目的主要是分离多余的泥沙，粒径明显区别于天然气水合物的杂质，以及破碎大体积的天然气水合物块以达到高效分离的要求。② 利用天然气水合物水力提升系统将经初步处理后的天然气水合物浆体通过软管、中继仓、硬管、泥浆泵输送至海平面的操作平台。③ 将海面附近的热海水与输送上来的天然气水合物进行混合、换热，使得天然气水合物的温度升高，发生分解。分解出的气体通过专门的集气罐进行收集，分离剩下的泥沙等杂质则通过排出管排回海里。图1为天然气水合物水力提升法的开采示意图。

目前，还没有一种最优的方法能够用于天然气水合物工业规模的实际开采。水力提升法相比于其他几种常规开采方法，不仅是我国海底采矿领域的重要研究成果，而且适用于南海天然气水合物藏的赋存情况。因此，天然气水合物的水力提升法具有现实的理论意义[9]。

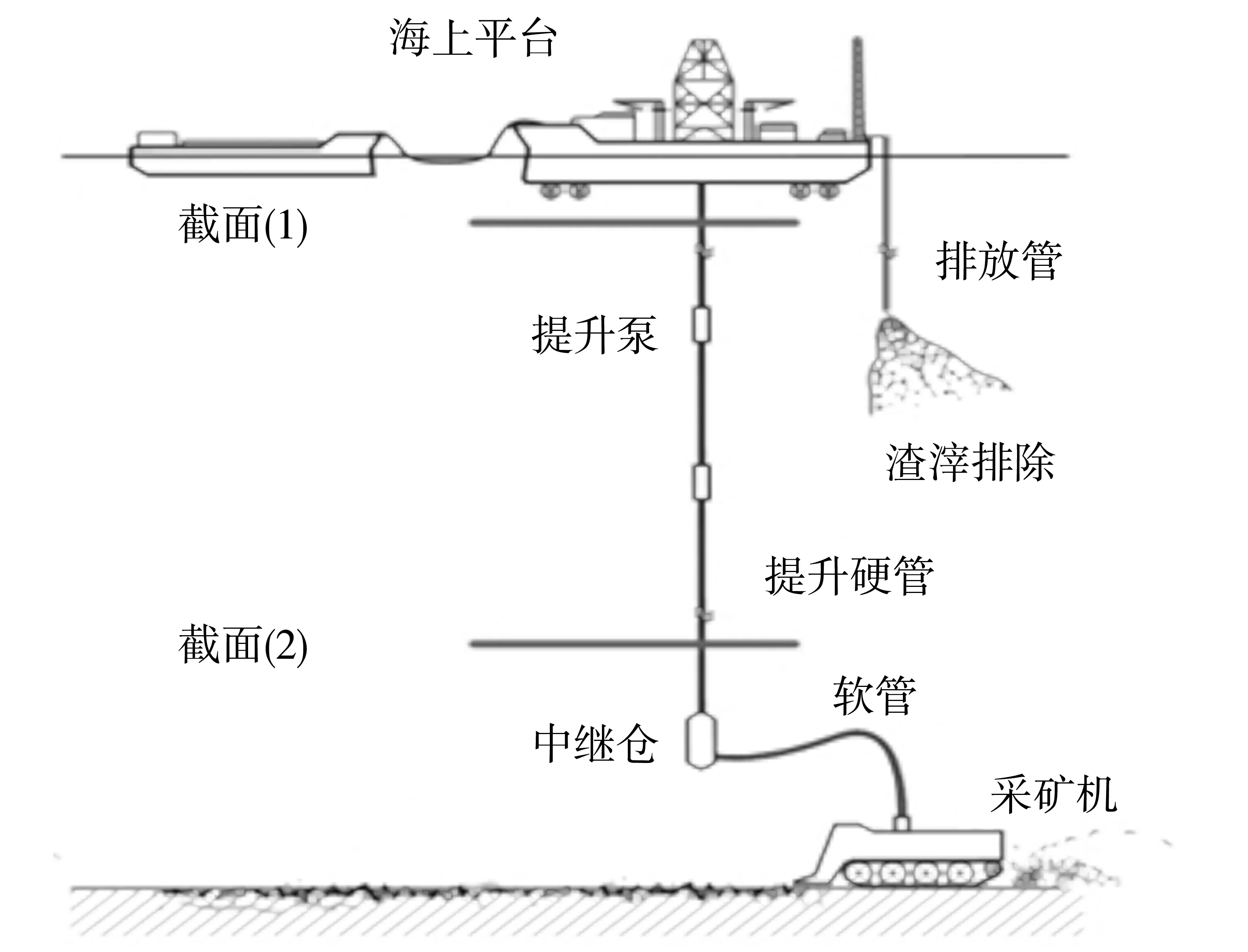
图1 天然气水合物水力提升管道系统Fig.1 Hydraulic lifting pipeline system of natural gas hydrate

2 基于水力提升法的最小提升速度

对于天然气水合物输送系统而言，需要选择合适的输送速度将天然气水合物从海底输送至海面平台。输送速度过小将不能向上输送天然气水合物颗粒，会导致堵管；因过快的速度会导致天然气水合物颗粒与管壁发生更多的摩擦和碰撞，输送速度过大不仅增大了能量消耗、降低了提升效率，而且存在堵管可能性。因此最小输送速度的确定是天然气水合物提升系统输送参数选择的首要环节之一。天然气水合物颗粒的最小提升速度与颗粒在管道中的运动状态、颗粒与管道相互作用、颗粒存在状态有关，主要受到湍流强度、阻力系数、颗粒质量分数、滑移速度的因素影响。

水力提升最小速度的计算方法有很多种。其中，最主流的方法是通过理想单颗粒的沉降情况计算单颗粒的沉降速度，再从单颗粒的沉降速度推测实际颗粒群的沉降速度，最后用颗粒群的沉降速度来推算颗粒的水力提升速度。本文结合天然气水合物的性质，运用主流的水力提升最小速度的计算方法研究了天然气水合物的最小提升速度。

均匀沉降时，静水中的球型单颗粒的受力情况如图2所示。即有：

(1)

图2 水力提升过程球型颗粒受力Fig.2 The force of spherical particles in the process of hydraulic lifting

式中ρs为球型颗粒密度，kg/m3；ρf为液体密度，kg/m3；vts为单个球型颗粒匀速沉降速度，m/s；CD为球型颗粒阻力系数，无量纲数。而:

(2)

其中，阻力系数CD直接决定着颗粒的最终沉降速度。影响阻力系数CD的因素很多，CD是雷诺数Re的函数，可表达为CD=fn(Re) ，具体如下[10]：

(3)

当颗粒为粗颗粒时，可得CD=0.44。若颗粒外部处于湍流状态，将CD带入公式(2)中可得到：

(4)

公式(4)是理想状态下球体粗颗粒的沉降速度。在实际生产过程中锰结核粗颗粒在静水中的沉降速度要比同直径大小的理想球状颗粒小得多，这主要是因为破碎后的锰结核表面并非球体，而是大小形状各异的颗粒。Stepanoff[11]的锰结核沉降实验表明：当锰结核的直径在1-30mm之间，且形状因子K=0.2时，其实际沉降速度需要在理想球型颗粒的最终沉降速度上乘以折降系数ξ。实验取ξ=0.4，得到锰结核的沉降速度为：

(5)

式中，ξ为折降系数；νt为颗粒实际沉降速度，m/s; 由于组成和成分的不同，在经过海底采矿车的铰刀破碎以后，天然气水合物颗粒和锰结核的形状、颗粒粒径都有所不同。一般情况下，经过铰刀破碎后的天然气水合物颗粒的粒径要比锰结核小。将天然气水合物颗粒的折降系数取为ξ=0.7，并将其带入公式(5)中，可得：

(6)

天然气水合物最小水力提升速度要在实际沉降速度上乘以一个安全系数以得到安全的最小提升速度。Sellgren[12]于1979年研究了最小提升速度与沉降速度的关系。实验结果显示：颗粒垂直输送时的最小水力提升速度要在颗粒沉降速度4倍以上。故：

(7)

式中，Vmin为颗粒垂直输送时水力提升最小速度，m/s。式(7)为目前常用的水力提升最小速度计算方法。金文斌等[13]通过实验得到了大颗粒在垂直管道中水力提升浮游速度的计算公式：

(8)

式中，d为颗粒直径，mm;D为管道直径，mm;CV为混合物中颗粒浓度。实际情况下，取最小水力提升速度为浮游速度的两倍，得：

(9)

申焱华等[14]研究了粒径管径比、颗粒群浓度、湍流强度对阻力系数CD的影响，并给出了适用于工业生产的水力提升最小速度的计算公式：

(10)

式中，Vso为颗粒理想情况下的沉降速度，m/s；Cdo为理想情况下锰结核沉降的阻力系数。Cd为临界锰结核阻力系数。理想情况下Cd应该取0.445，但考虑船体的运动，管道受到海水波动的影响、颗粒输送时内部流场的变化，且当雷诺数Re>105阻力系数CD急剧减小到达临界值0.1。将Cd=0.1，带入公式(10)可得：

(11)

实验测定的锰结核阻力系数CD不是定值，而是在0.65～2.5的范围内变化[12]。所以，用形状系数来计算阻力系数，得：

(12)

式中，Sf为形状系数。长沙矿冶院通过实验得到的锰结核形状系数Sf=0.8，与(12)式对应的Cd=0.8383。同等情况下，提升系统中天然气水合物的形状系数应取Sf=0.92，而对应的天然气水合物沉降阻力系数Cd=0.654，带入式(11)可得：

(13)

天然气水合物颗粒最小提升速度为3倍天然气水合物沉降速度，即：

(14)

通过以上3种最小水力提升速度的计算方法，分别得到 Sellgren最小提升速度为1.69 m/s；金文斌最小提升速度为0.656 m/s；申焱华最小提升速度为1.04 m/s。可以得出，金文斌最小提升速度的偏差较大。考虑到最不利于输送的工况，选择较大的1.69 m/s为天然气水合物水力提升最小输送速度。

3 水力提升系统建模

天然气水合物水力提升过程可视为恒温过程，但管道内压力却呈逐渐降低的趋势。当压力减小一定程度时，水合物开始分解。天然气水合物在输送的过程中分解生成的气泡减小了水力提升过程的运行阻力[15-16]。设天然气水合物管道内提升系统内的流体为均匀混合的不可压缩流，做定常流动；管道内固液两相均为连续相，每相的物理特征为定值，不考虑相变。在图1中提升管道的任意两个截面1、2之间列出固液两相流的伯努利方程[17]。

(15)

式中，ρm为浆体的密度，kg/m3;vm1、vm2分别为截面1、2的浆体流速，m/s2；αm1、αm2为截面2的动能修正系数；P1、P2分别为截面1、2处的静压，Pa；h1、h2分别为截面1、2的高度，m；Δpm为沿程压力损失，Pa。

4 管道压力损失

一般情况下，天然气水合物浆体采用的高浓度输送。浆体的颗粒直径、密度、粘度、颗粒形状、管道直径、管道摩擦、颗粒粒径分布情况等都会对输送过程和压力损失造成影响。从20世纪20年代开始，Gagsterstadt等研究了颗粒垂直提升摩阻损失。随后，相关学者陆续提出了Cloet摩阻公式，Worster摩阻公式等。本文采用夏建新等[18]提出的摩阻计算公式。夏建新等[18]将垂直管道的原理损失分为摩阻损失if、由清水和提升混合物密度差形成的位能损失is、以及由颗粒间碰撞产生的内部附加能量损失ic。则:

it=if+is+ic

(16)

式中，it为压力损失，Pa。结合夏建新压降模型，利用工程计算软件MATLAB，研究管径，颗粒直径、颗粒浓度、输送速度等关键参数对压降的影响。

4.1 输送速度对压力损失的影响

夏建新压降计算模型是建立在锰结核提升过程基础上的压降模型，它同样也适用于天然气水合物深海开采。取颗粒直径d=15 mm，颗粒输送体积浓度CV=0.2，D=300 mm，研究浆体流速对压降的影响，计算结果如图3-4所示。

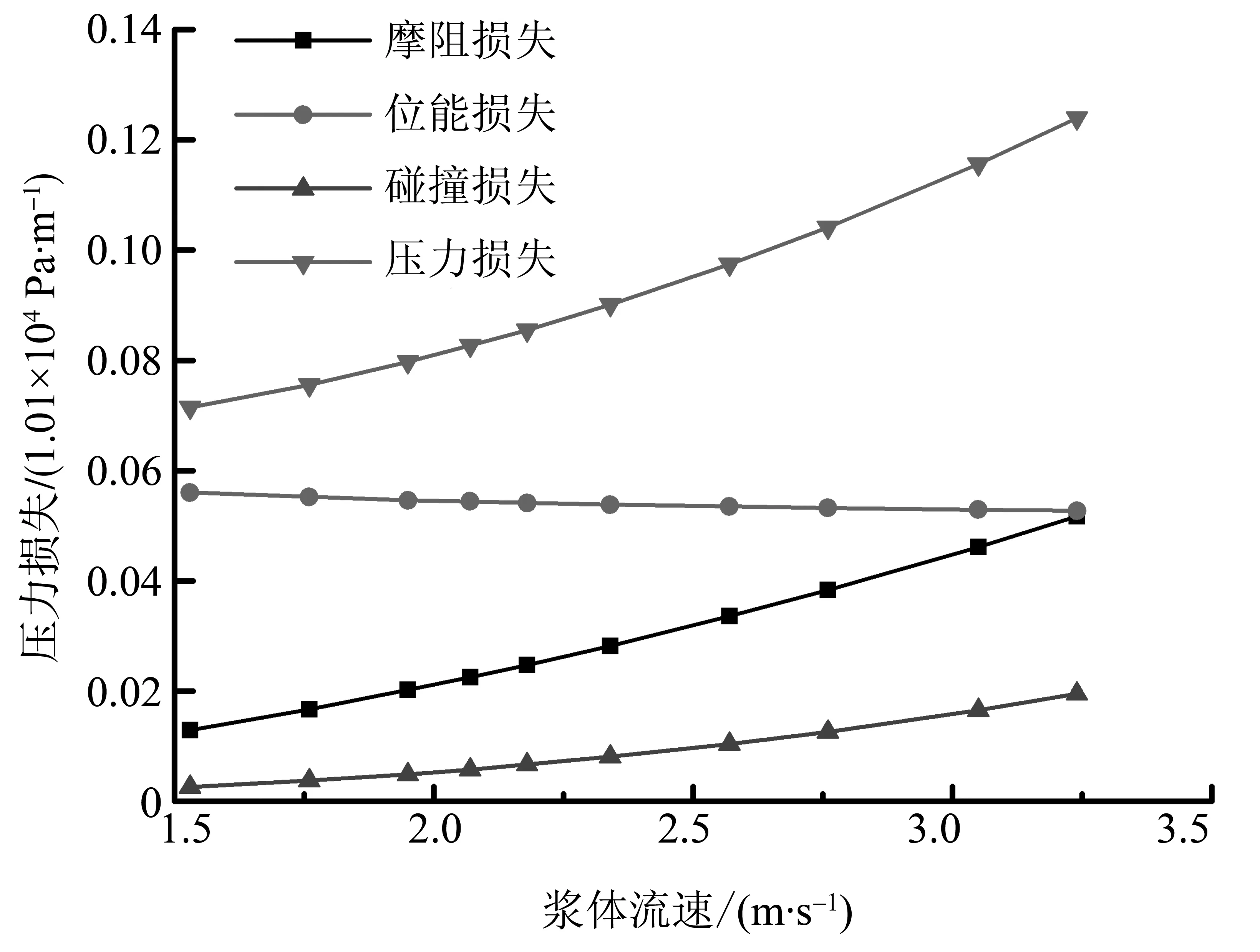
图3 各项压力损失随浆体流速的变化曲线Fig.3 The pressure loss varation with slurry flow rate

图4 各项压力损失的占比随浆体流速的变化曲线Fig.4 The pressure loss ratio varation with slurry flow rate

如图3所示，摩阻损失、碰撞损失和压力损失与浆体流速成正比。从图4能够看出压力损失主要是由位能损失导致的，其次是摩阻损失；内部附加能导致的能量损失只占很小的一部分。而浆体流速与摩阻损失百分比和碰撞损失百分比成正比，与位能损失成反比。不同管道直径下各项损失随流速的变化情况如图5-8所示。

图5 不同管径时，摩阻损失随浆体流速的变化曲线Fig.5 The friction loss varation with slurry flow rate when pipe diameters is changed

图6 不同管径时，位能损失随浆体流速的变化曲线Fig.6 The potential energy loss varation with slurry flow rate when pipe diameters is changed

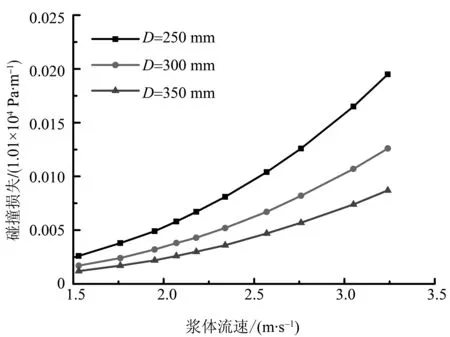
图7 不同管径时，碰撞损失随浆体流速的变化曲线Fig.7 The collision loss varation with slurry flow rate when pipe diameters is changed

图8 不同管径时，总压力损失随浆体流速的变化曲线Fig.8 The total pressure loss varation with slurry flow rate when pipe diameters is changed

由图5可得：不同管径时，摩阻损失均随着浆体流速的增加而变大。如图6所示，位能损失与流速成反比关系。当速度值从1.53 m/s升至3.24 m/s时，位能损失变化量比内部附加能损失小得多，相对于摩阻损失更是可忽略不计。位能损失主要是由清水和提升混合物之间的密度差造成的，管道直径对提升系统中的位能损失没有太大影响。由图7可得：碰撞能量损失与浆体流速成正比。管道直径为250 mm时，随着速度值从1.53 m/s升至3.24 m/s，内部附加能量损失增加了6倍多。这是因为颗粒间相互作用受管道内流动状态的影响。浆体速度越大，湍流强度就越大，颗粒间的相互碰撞作用越明显，所耗散的能量越多。总压力损失主要由摩阻损失和位能损失所构成。随着速度增大，摩阻损失增大，位能损失减小，内部附加能量损失增大。因此，总压力损失随着浆体流速的增大而持续增加，如图8所示。

4.2 浆体浓度对压力损失的影响

当颗粒直径d=15 mm，管道直径D=300mm，输送速度vm=2.5 m/s时, 改变浆体浓度，四种能量损失计算结果如图9-10所示。

图9 各项压力损失随浆体浓度的变化曲线Fig.9 The pressure loss varation with slurry concentrations

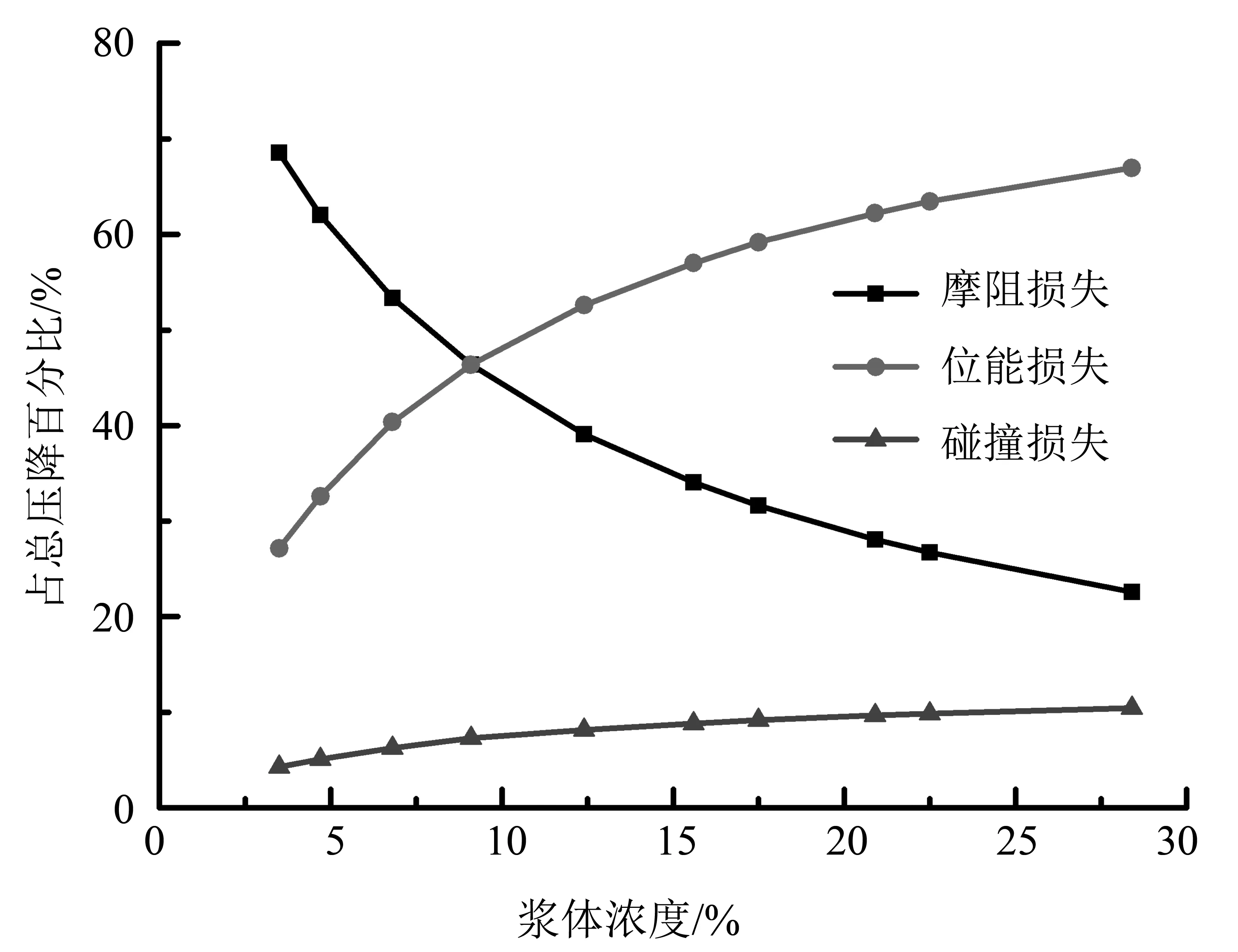
图10 各项压力损失占比随浆体浓度的变化曲线Fig.10 The pressure loss ration varation with slurry concentrations

由图9可得：随着浆体浓度的增大，摩阻损失不变，其他几种能量损失增大。每种能量损失都与浆体浓度的改变成线性关系。相对于流速，位能损失对浆体浓度的改变更为敏感。由图10可得：当浆体浓度较小时，压力损失大部分由位能损失和摩阻损失构成，碰撞能量损失只占很小一部分。随着浆体浓度增大，位能损失和碰撞能量损失的占比增大。不同管道直径下，各项损失随浆体浓度的变化情况如图11-14所示。

图11 不同管径时，摩擦阻力损失随浆体浓度的变化曲线Fig.11 The friction resistance loss varation with slurry concentrations when pipe diameters is changed

由图11可得：在相同的浆体浓度下，提升管道单位长度摩阻损失随着管道直径的变小而增大。在图12中，单位长度碰撞能量损失与浆体浓度成正比，这是因为浓度越大单位体积内颗粒数目越多，颗粒碰撞频率增大。随着管径的减小，相同浆体浓度下单位长度碰撞损失并非呈线性增长，在浆

图12 不同管径时，碰撞损失随浆体浓度的变化曲线Fig.12 The collision loss varation with slurry concentrations when pipe diameters is changed

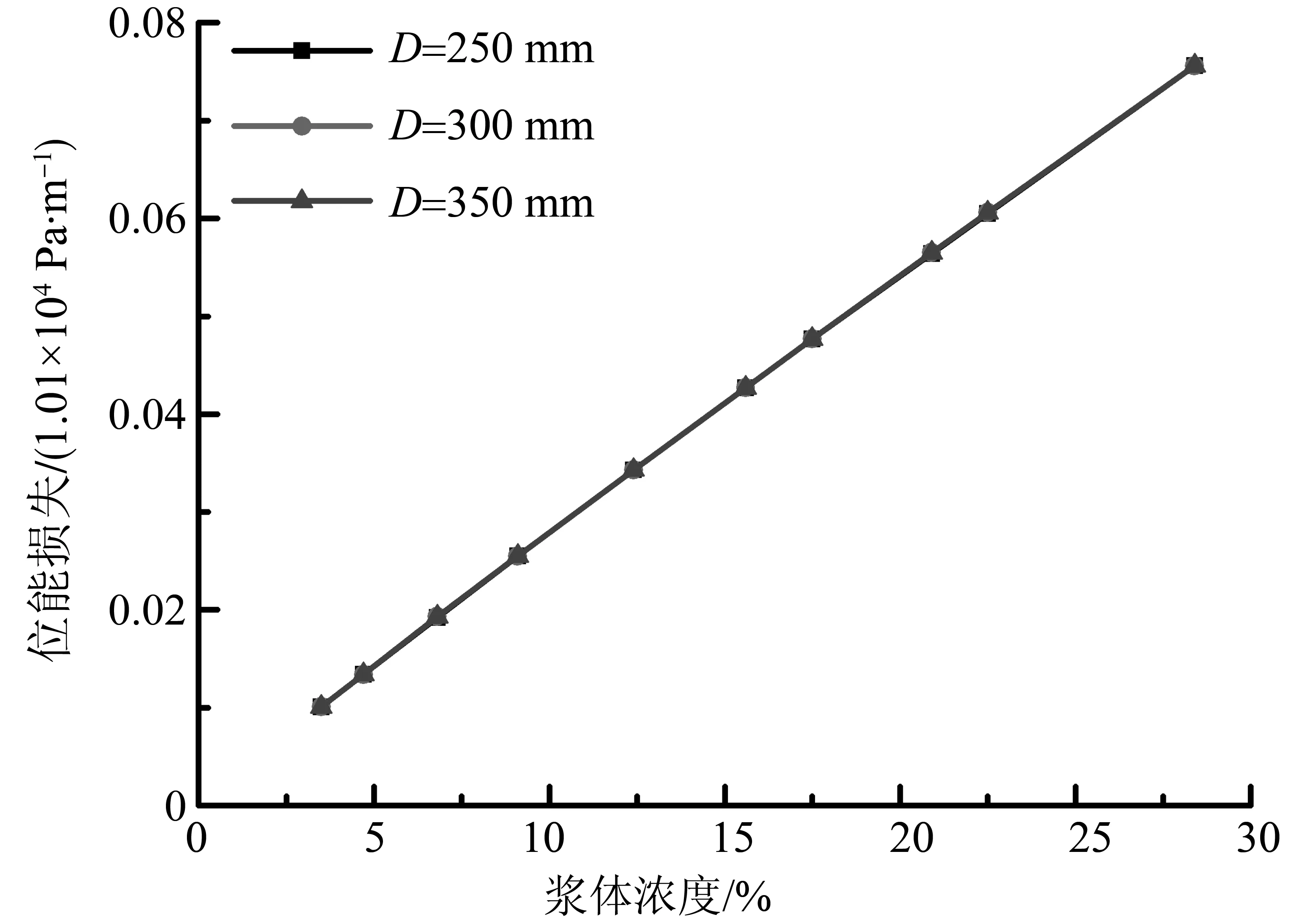
图13 不同管径时，位能损失随浆体浓度的变化曲线Fig.13 The potential energy loss varation with slurry concentrations when pipe diameters is changed

图14 不同管径时，总压力损失随浆体浓度的变化曲线Fig.14 The total pressure loss varation with slurry concentrations when pipe diameters is changed

体浓度较大时更是如此，这是因为颗粒碰撞耗散的能量和颗粒半径的平方相关，是非线性的。如图13所示，位能损失与浆体浓度成正比，呈线性关系。而管径对单位长度位能损失影响极小。在图14中，总压力损失与浆体浓度呈线性关系。这是因为位能损失在总压力损失占较大的部分，而在相同浆体浓度下，随着管道直径的增大单位长度的压力损失是减小的。

4.3 颗粒直径对压力损失的影响

当浆体浓度CV=0.2；颗粒输送速度为v=2.5 m/s；管道直径D=300 mm时，不同颗粒直径下的能量损失如图15-16所示。

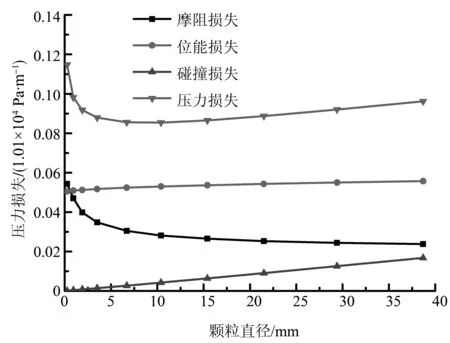
图15 各项压力损失随颗粒直径的变化曲线Fig.15 The pressure loss varation with particles diameter

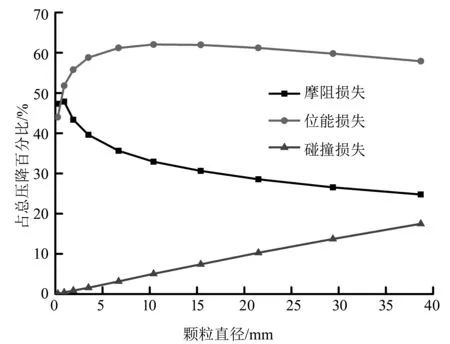
图16 各项压力损失占比随颗粒直径的变化曲线Fig.16 The pressure loss ratio varation with particles diameter

由图15可得：随着颗粒直径增大，位能损失、碰撞损失增大，摩阻损失减小，而总压力损失呈先减小后增大的趋势。位能损失虽然随着颗粒直径增大而增大，但其改变量相对于其他项可忽略不计。在图16中，碰撞损失在压力损失中占比最小。颗粒直径很小时，压力损失基本由位能损失和摩阻损失构成，但随着颗粒直径逐步增大，摩阻损失所占比例开始急剧变小，而碰撞损失所占比例逐渐增大。不同管道直径下，各项能量损失随颗粒直径的变化情况如图17-20所示。

在图17中，摩阻损失随颗粒直径的增长呈现出一个先快速减小再缓慢减小的趋势。同时，随着输送管径的增大，单位长度摩阻损失却减少了。在图18中，位能损失与颗粒粒径成正比。在图19中，碰撞损失与颗粒直径呈现线性增加的态势。而相同颗粒直径条件下，管径的增大降低了颗粒碰撞能量损失。在图20中，单位长度压力损失对颗粒直径的变化可分为两个阶段，第一个是急速下降阶段，第二个是缓慢上升阶段。急速下降主要是因为摩阻损失急速下降的原因导致了总压力损失的急速下降。

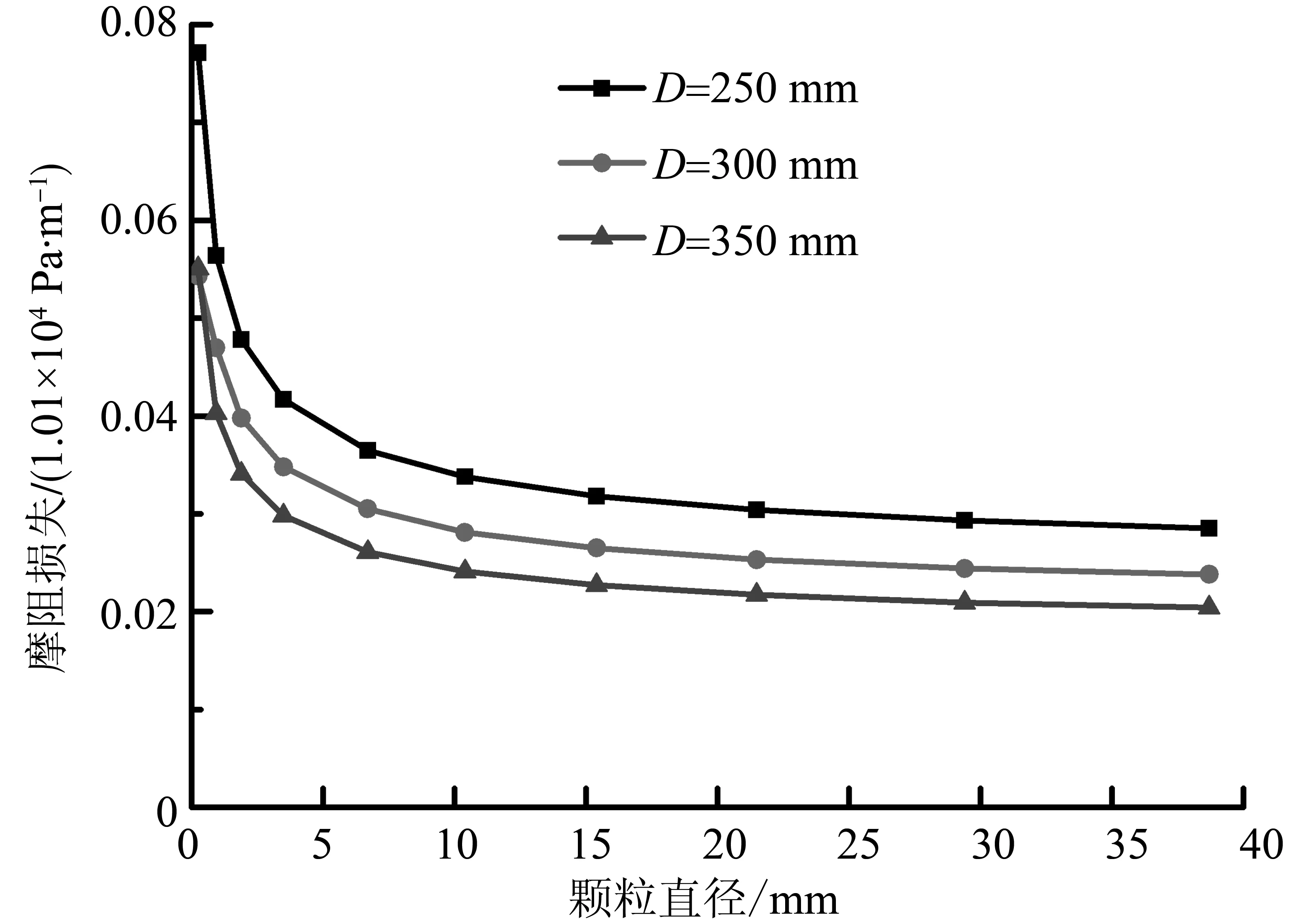
图17 不同管径时，摩擦阻力损失随颗粒直径的变化曲线Fig.17 The friction resistance loss varation with particles diameter when pipe diameters is changed

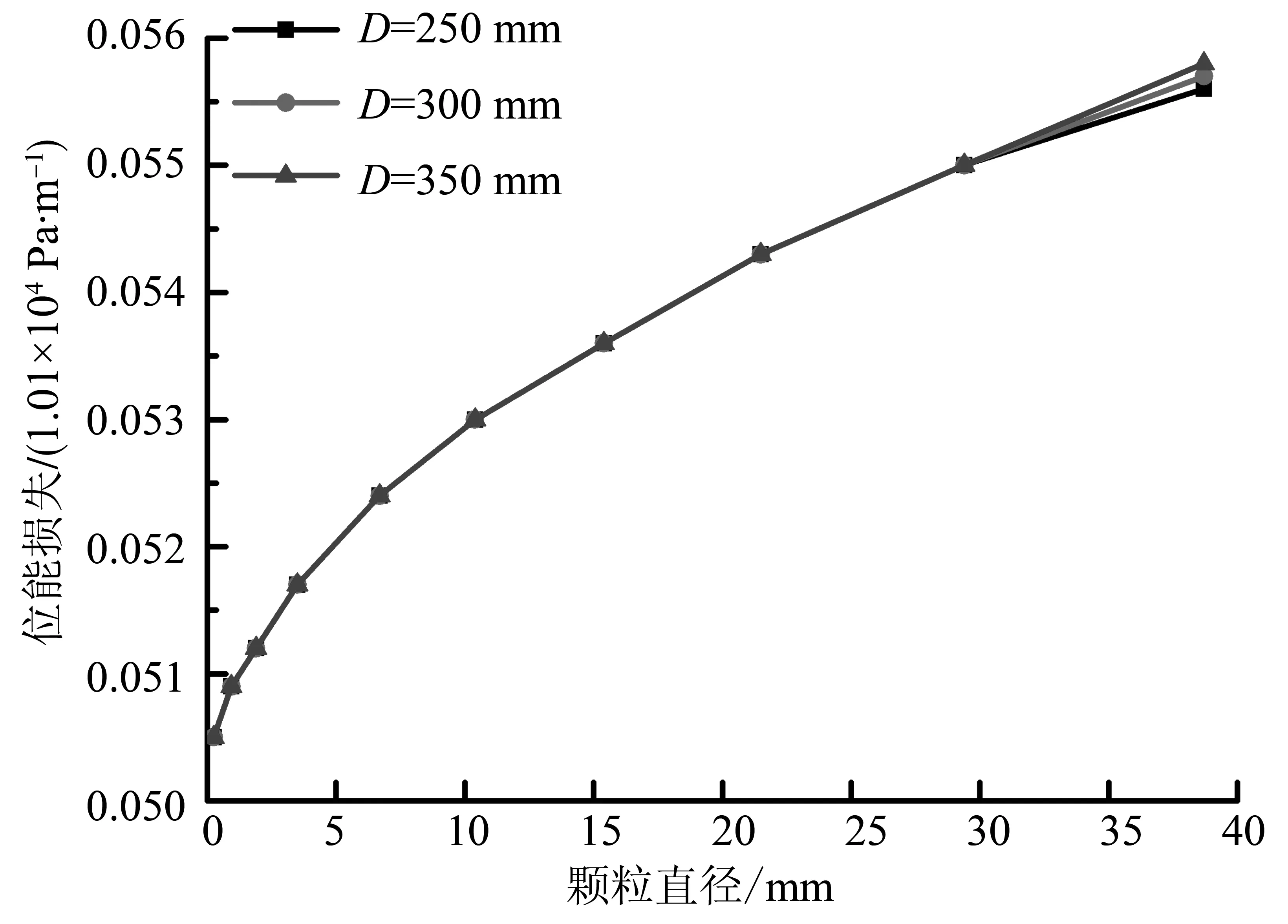
图18 不同管径时，位能损失随颗粒直径的变化曲线Fig.18 The potential energy loss varation with particles diameter when pipe diameters is changed

图19 不同管径时，碰撞损失随颗粒直径的变化曲线Fig.19 The collision loss varation with particles diameter when pipe diameters is changed

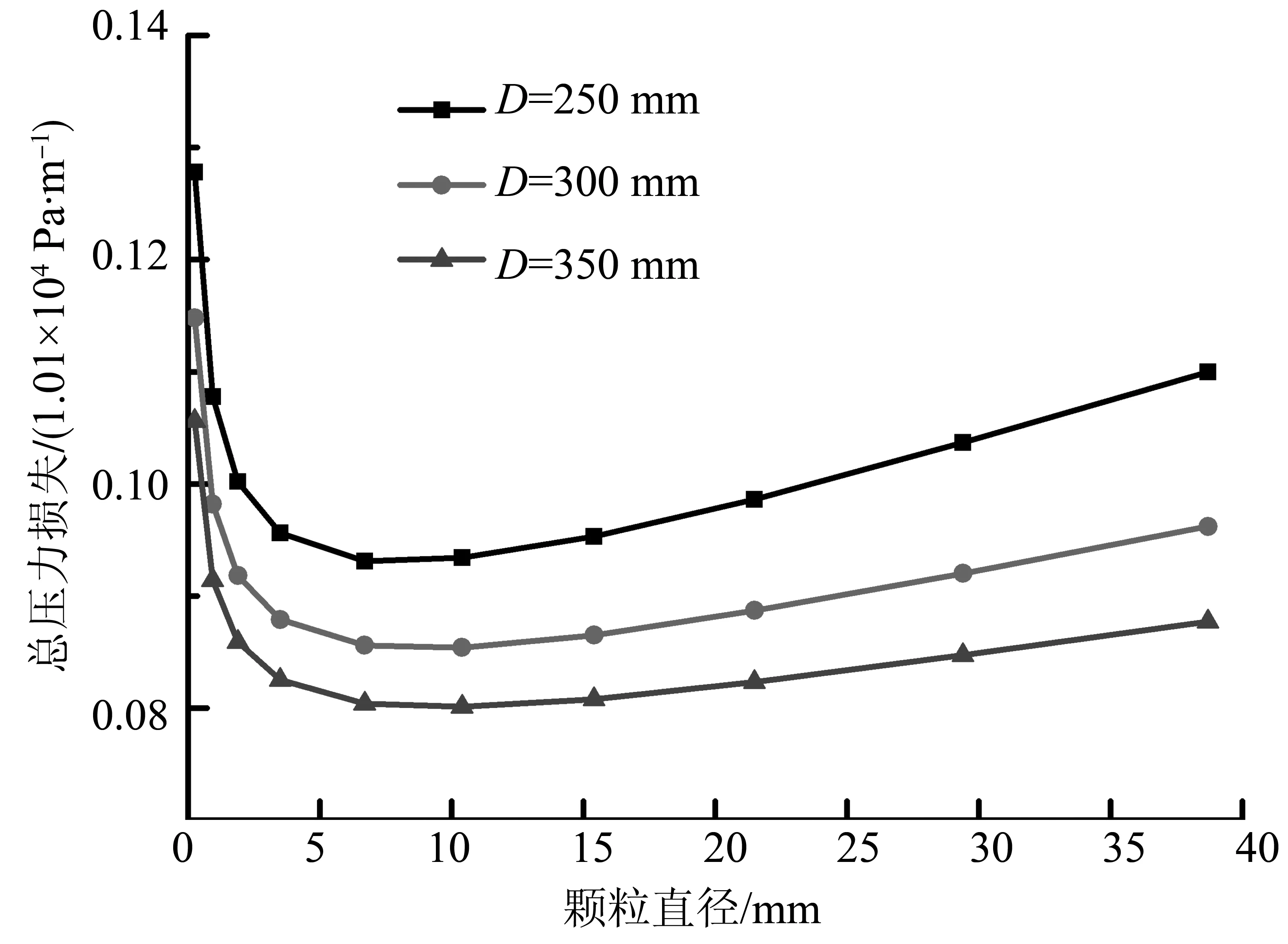
图20 不同管径时，提升压力损失随颗粒直径的变化曲线Fig.20 The total pressure loss varation with particles diameter when pipe diameters is changed

5 总 结

本文讨论了适合于天然气水合物颗粒特征的最小提升速度计算方法。采用3种不同的方法对天然气水合物颗粒提升最小速度进行了计算，得到金文斌公式的计算结果为0.656 m/s，Stepanoff A J公式的计算结果为1.69 m/s，申焱华公式的计算结果为1.04 m/s。考虑到深海的恶劣环境，选取最大值1.69 m/s作为天然气水合物水力提升的最小速度。且实际提升流速应比1.69 m/s略大更为合适。

基于天然气水合物提升管路系统，分析对比了国内外垂直输送系统提升压损的计算方法。结合夏建新的压降模型，利用MATLAB工程软件得到了不同工况下压力损失的数值解，研究了颗粒直径、输送浓度、输送速度对提升压降的影响及其变化规律。研究结果对实际操作和下一步的研究具有现实的指导意义。

[1] 钱伯章，朱建芳. 天然气水合物-巨大的潜在能源[J]. 天然气与石油，2008,26(4)：47-52. QIAN B Z, ZHU J F. Gas hydrate-huge potential energy [J]. Natural Gas and Oil, 2008,26(4):47-52.

[2] 姚伯初. 南海天然气水合物的形成条件和分布特征[J]. 海洋石油,2007,27(1):1-10. YAO B C. Formation and distribution of gas hydrate in the South China Sea [J].Offshoreoil,2007, 27(1):1-10.

[3] 张新军,天然气水合物藏降压开采实验与数值模拟研究[D]. 青岛:中国石油大学(华东),2008. ZHANG X J. Experimental study and numerical simulation on depressurization of gas hydrate reservoir [D]. Qingdao: China University of Petroleum (Hua Dong), 2008.

[4] 姚宇澄,殷福珊. 天然气水合物研究进展[J]. 化学进展,1997,9(3):99-106. YAO Y C,YIN F S . Research progress of natural gas hydrate [J].Progress in Chemistry, 1997, 9(3):99-106.

[5] 唐良广,李刚,冯自平,等. 热力法开采天然气水合物的数学模拟[J]. 天然气工业,2006,26(10) :105-107. TANG L G, LI G, FENG Z P, et al. Mathematical simulation of thermal recovery of natural gas hydrate [J]. Journal of Natural Gas Industry, 2006,26(10):105-107.

[6] OHGAKI K, SANAGAWA H, MATSUBAR A. Methane exploitation by carbon dioxide from gas hydrates-phase equilibria for CO2-CH4mixed hydrate system[J]. Chem Eng Jpn,1996，29(3)：478-483.

[7] DEAN LOVELL，PAKUL SKI M. Hydrate inhibition in gas wells treated with two low dosage hydrate inhibitors[C]∥ Proceedings of the SPE International Symposium on Gas Technology.Alberta,Canada:SPE, 2002.

[8] 唐良广,冯自平,李小森,等. 海洋渗漏型天然气水合物开采的新模式[J]. 能源工程, 2006,25(1):15-18. TANG L G, FENG Z P, LI X S, et al. A new model for the exploitation of marine leaky gas hydrate [J].Energy Engineering,2006, 25(1):15-18.

[9] 徐海良,林良程,吴万荣,等. 海底天然气水合物绞吸式开采方法研究[J]. 中山大学学报(自然科学版), 2011,50(3):48-52. XU H L, LIN L C,WU W R, et al. Cutter-suction exploitation mode of marine gas hydrate [J].Acta Scientiarum Naturalium Universitatis Sunyatseni, 2011,50(3):48-52.

[10] 费祥俊.浆体与粒状物料输送水力学[M]. 北京：清华大学出版社, 1994.

[11] STEPANOFF A J. Pumps and blowers, selected advanced topics: two-phase flow [M]. New York: Wiley, 1965.

[12] SELLGREN A. Slurry transportation of Ores and industrial minerals in a vertical pipe by centrifugal pumps-A pilot-plant investigation of hydraulic hoisting [D]. Dept of Hydraulics，Chalmers University of Technology，1979.

[13] 金文斌,黄小平,高文鹏. 大颗粒物料在垂直管道内最小输送速度的试验研究[J]. 矿业研究与开发,1997,17(2):17-20. JIN W B, HUANG X P,GAO W P. Experimental study on the minimum conveying velocity of large particles in vertical pipeline [J]. Mining Research and Development,1997,17(2):17-20.

[14] 申焱华,毛纪陵,凌胜. 垂直管道固液两相流的最小提升水流速度[J]. 北京科技大学学报,1999,21(6):519-522. SHEN Y H, MAO J L,LING S. The minimum lifting water velocity of solid liquid two phase flow in vertical pipeline [J]. Journal of University of Science and Technology Beijing,1999,21(6):519-522.

[15] 李文华. 空气助送泥技术的研究与应用[J]. 中国水运,2002,11(2):16-17. LI W H. Research and application of air assisted mud feeding technology [J]. China Water Transport.2002,11(2):16-17.

[16] 郑永刚,方铎,李桂芬. 圆管流掺气减阻理论研究[J]. 水动力学研究与进展(A辑), 1996,13(2):161-170. ZHENG Y G, FANG D,LI G F. Theoretical study on drag reduction by gas flow in a circular tube [J]. Chinese Journal of Hydrodynamics (A), 1996,13(2):161-170.

[17] 佟庆理. 两相流动理论基础[M]. 北京：冶金工业出版社,1982.

[18] 夏建新,倪晋仁,黄家桢. 锰结核在垂直管路输送过程中的压力损失[J]. 泥沙研究, 2002,27(2):23-28. XIA J X, NI J R,HUANG J Z. Pressure loss of manganese nodules in vertical pipeline transportation [J]. Journal of Sediment Research, 2002,27(2) :23-28.

The minimum lifting speed and pressure loss of the natural gas hydrate in the seabed

CHENHao,FULaiqiang,LÜBin,WUWenke,HUANGJunming

(School of Mechatronic engineering, Southwest Petroleum University, Chengdu 610500, China)

According to the correlation properties of natural gas hydrate, several main methods of exploitation of natural gas hydrate are compared and summarized. Based on the current theory on hydraulic lifting process of the natural gas hydrate, the minimum lifting speed of the natural gas hydrate particles is studied, and the minimum velocity was calculated by using the theory of the minimum velocity of hydraulic lifting with the natural gas hydrate particles. The theoretical modeling of the pipeline transportation system of the hydraulic lifting system is carried out, and used to study the effects of particle size. The particle diameter is studied, and compared with that on the pressure drop of gas hydrate in the pipeline system.

nature gas hydrate；hydraulic lift；the minimum lifting speed；pressure drop

10.13471/j.cnki.acta.snus.2017.03.003

2016-06-14 基金项目：中国工程院自然基金(2013-04-ZCQ-002)；国家级重点实验室开放基金(PLN1418)

陈浩(1963年生)，男；研究方向：现代设计理论和机械工程设备；E-mail:ch91668@163.com

付来强(1991年生)，男；研究方向：化工过程机械；E-mail:flqswpu@163.com

TE

A

0529-6579(2017)03-0017-09