探析循射构建空间想象
湖南省长沙外国语学校k1402(410000)
向南燊●
探析循射构建空间想象
湖南省长沙外国语学校k1402(410000)
向南燊●
本文在分析循射影构建空间想象的基础上,探究循射影构建空间想象的措施,并提出循射影构建空间想象的原则.
循射影;直观图;三视图
立体几何是高中学生普遍感到头疼的一门学科,它的核心任务是培养学生的空间想象能力,将学生能力上升到在复杂图形中分离出简单图形,将具体的几何体内化成潜意识的点线面,能在思维迁移上化无形为有形,化有形为无形,也就是几何学在几何地图上翻译成心智上的“图论”.现行普通高中课程标准实验教科书数学必修二第一章《空间几何体》在第一页粗略介绍了几何学及章节梗概.这样描述道:“几何学是研究现实世界中物体的形状、大小与位置关系的数学学科.本章我们从对空间几何体的结构特征、三视图和直观图,了解一些简单几何体的表面积和体积的计算方法.”教材鲜明地阐明了几何入门先是抓住学生的视线入手,感性上由表及里,由此及彼,从而构建空间想象的表象及抽象.结合教科书编写意图以及自己学立体几何的方法,综合三视图、射影图,遵循高中生感知几何体的视线.我觉得认知的底片主要是在射影生成上.
一、核心概念的界定
射影是光线透过几何体后,在控制屏面上留下的影子,我们把光线叫投影线,把留下物体影子的屏幕叫投影面.射影实质上是一种原像与像的映射,是流体几何入门的一种简单函数关系.在投影的组合体上,立体图形平面化,反过来,我们能够根据平面图形想象空间几何体的形状和结构.射影过程是一种动态与静态的矛盾统一.而空间想象核心就是形象思维加上所感知的空间表象,形成记忆,产生联想.能脱离几何实体在心智中形成空间想象.本论述是指在老师的视线与学生的视线中构建空间图论,提高学生空间想象能力,收到良好的教学成效.
二、循射影构建空间想象的措施
“横看成岭侧成峰,远近高低各不同.”这说明从不同角度看同一物体视觉效果可能不同.要比较真实地反映出物体的结构特征,我们须对射影的位置与形体的估量.空间想象能力就是能从定性定形定量上持久地再现空间点线面体.高一学生初涉及立体几何,感知空间物体一是模糊,二是感知片面,三是位置错乱,怎样才能提高空间想象能力,学好立体几何呢?请看我的经验.
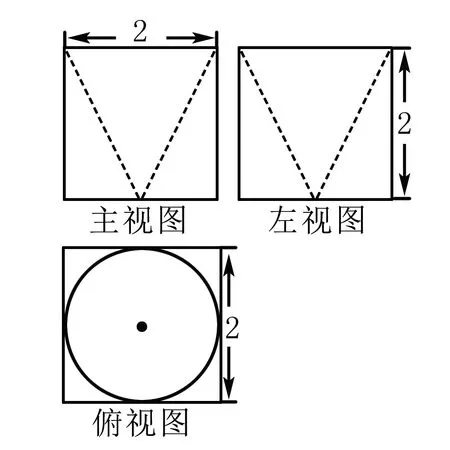
1.结合具体几何体作好三视图,即根据三视图还原出直观图.三视图是几何入门的路标,能多角度刻画几何体,要把握三视图的实质——正视等高等长,俯视等长等宽,侧视等宽等高,选取射影参照片有边际成像法,即把握空间临界点临界线,将几何体刻画在衬托面上;有抽截面成旬法,旋转体三视图实质上是轴截面成旬;有压缩成像法,将几何体压缩成平面图.学三视图要循序渐进,由简到繁,先由简单几何体成像再到简单组合体成像再到多倍体成像,使认知步步加深,空间想象能力层层深入,能上升到换位思考,将三视图再现空间图.三视图是现代教学构建主义的真实写照,能使感知材料由具体化到抽象化.如:(2011陕西理5)某几何体的三视图如图所示,则它的体积是( )
这个高考题就要求我们能很好地根据三视图还原好直观图.
2.结合直观图,实现图形的换位,建立空间图形的函数关系,将感知理性化.要弄懂直观化的理念,必须从三个维度把握变量关系,空间虚实关系,要把握“横竖假不了,纵的真不了”的作图规律,要将作法作为重点,不能颠倒“写作”关系,先写作法再作图,先作多面体再画球体,再画内切与外接几何体,同步计算几何体相关面积与体积,达到定位、定形、定量的自然统一.如:
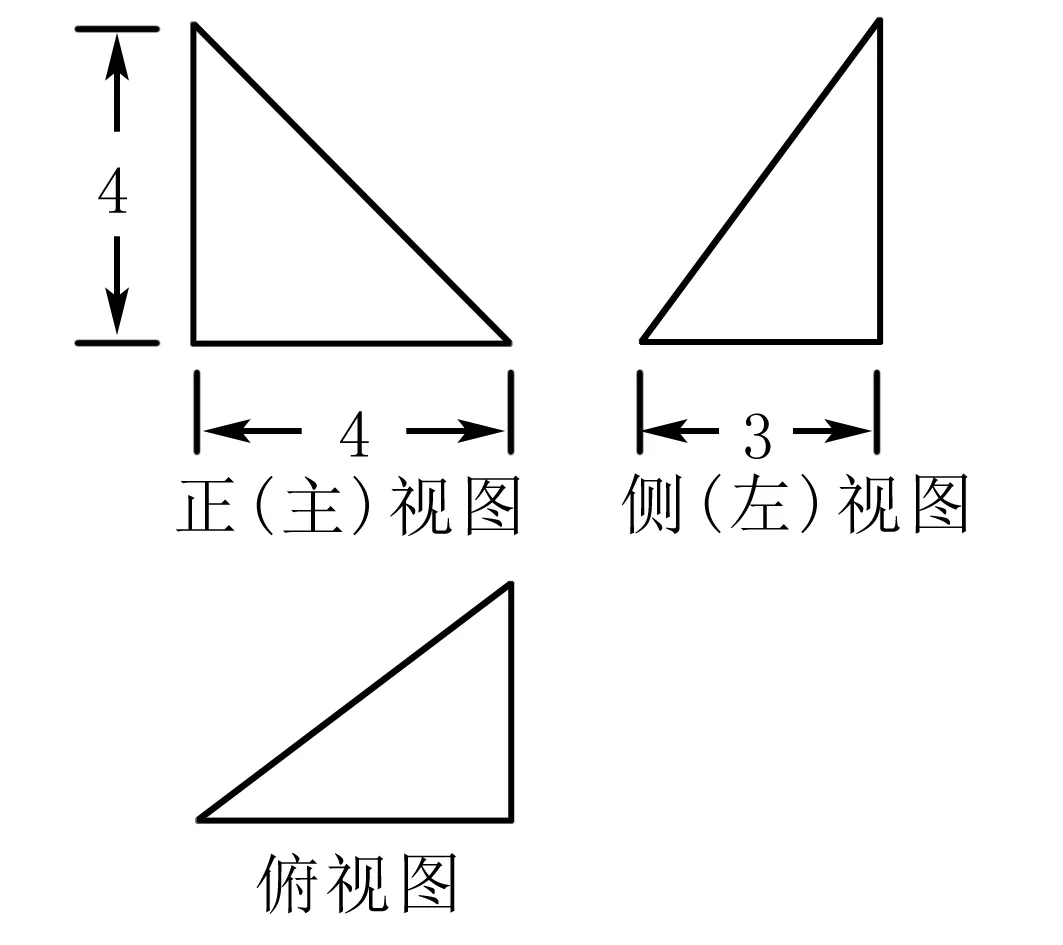
(2011北京理7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( ).
这个高考题就要求我们能从三个维度把握数量关系,进而进行计算.
3.结合物理折射规律弄通几何体对折问题,使学生懂得同面长不变,角不变.异面前实后虚,懂得虚实的内涵.从复杂图形中分离出简单图形.
4.结合光线的平铺规律,在几何体侧面展开图教学中,明确曲直的变换关系,由圆到线,同时由线到圆,要把握侧面横向与纵向的延展程度,会求曲面展开图中的最短距离.如:

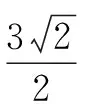

这个高考题就要求我们能化曲为直,把球面距离问题转化为三角形中的问题解决.
5.结合平移特殊线,特殊面或补图法.将异面问题化为共面问题,在计算中讲究计算简单化作证求程序后整法,边解数值特殊法,化繁为简,由浅入深,由表及里.
三、循射影构建空间想象的原则
循射影构建空间想象实质上就是遵循高中生的感知水平,抽象能力,有的放矢,逐步提高空间想象能力,学习时具体要遵循以下四个原则:
1.具体性与抽象性相结合的原则.教学中,教师都会准备好实体模型,让我们从直观上感知、观察、洞悉几何体,并且还会用多媒体教学使几何体虚实分明,由表及里,由外到内,由简到繁,由浅入深地进行讲解,通常还会系统地由点扩充到面,由平面向量到空间测度,所以我们首当其冲是要树立起立体观念,使自己的感知由具体到抽象.
2.要坚持理论与实际相结合的原则.要培养自己的画图能力,联系现实空间、生活空间、建筑空间会作简单设计图,会进行简单的建筑预算、工程预算,达到数学与应用的统一,真正体现数学的“有用性”“准确性”“现实性”.
3.要处理好主观与客观的辩证关系.主观上看,平面好像有大小,而实际上是无穷空间的缩影;主观上看似钝角而实际中却是锐角,所以要认清几何构图中虚实的关系、曲直的关系等.
4.要处理好严谨性与量力性的关系.三维空间不能扩充到四维,避免复杂的计算,尽可能在直角三角形或等腰三角形或正方形中求角求边不必将射影变换变成位似变换.
总之,稳定的感知形成需有清晰的支撑面,通过归纳判断综合,而将空间想象面扫描形成知识底片,这样空间想象就在一个清晰的屏幕上使几何图形历历在目、一目了然,空间想象能力自然就提高了.
[1]魏志强.浅谈构建空间想象能力[J].学苑教育,2015(07)
G632
B
1008-0333(2017)01-0052-02

