提炼结论创新应用——圆锥曲线中弦的斜率与中点坐标关系的探究

李红玲●

提炼结论创新应用
——圆锥曲线中弦的斜率与中点坐标关系的探究

湖北省孝感市湖北航天高级中学(432100)

李红玲●

圆锥曲线是高考的重要考点之一，尽管教材和教学大纲主要强调的是通性通法，但由于圆锥曲线问题按通性通法处理往往运算量较大，过程繁琐，不易算对，所以根据圆锥曲线的常见问题总结反思，适当提炼一些实用的结论，可大大简化过程、减小运算量，特别是解选择填空题，运用这些结论解题可取得事半功倍的效果.下面根据圆锥曲线的常见问题探究弦的斜率与中点坐标的关系，提炼出几个结论供大家参考.

结论1 若直线l：y=kx+m(m≠0)与曲线(椭圆或双曲线)Ax2+By2=1相交于P、Q两点,弦PQ的中点为M(xm,ym)，则弦的斜率与中点坐标有如下关系：

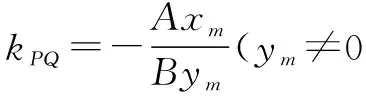
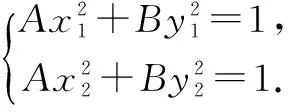
A(x1+x2)(x1-x2)+B(y1+y2)(y1-y2)=0，即2Axm(x1-x2)+2Bym(y1-y2)=0.

当ym=0时，若x1=x2，则PQ⊥x轴，kPQ不存在，与条件不符，故x1≠x2，则xm=0，直线l过原点，m=0，这与条件“m≠0”矛盾，从而ym≠0.所以

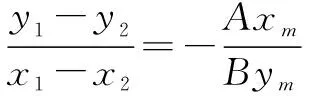
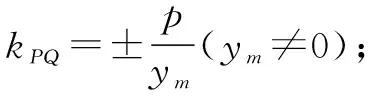
在结论1中，为了使结论简洁、统一好记，使用了椭圆和双曲线的统一方程Ax2+By2=1，而不是用a,b表示的标准方程，其中当A>0,B>0，且A≠B时，方程表示椭圆，当AB<0时表示双曲线，故结论1对中心在原点，以坐标轴为对称轴的椭圆和双曲线均可使用，结论2对于抛物线的四种形式的标准方程都可以使用.使用这些结论解决圆锥曲线中与中点弦相关的问题比传统方法要简便快捷，下面举例说明这些结论的应用.

应用1 求圆锥曲线被某点平分的弦所在直线方程

例2 求抛物线y2=4x被点(2,1)平分的弦所在直线的方程.

应用2 求圆锥曲线中平行弦中点的轨迹

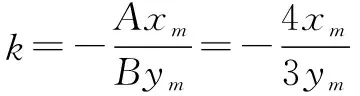
例4 求抛物线x2=4y中斜率为1的平行弦中点的轨迹.

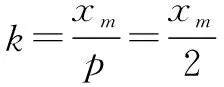
应用3 已知圆锥曲线的弦被某点平分，求圆锥曲线的方程

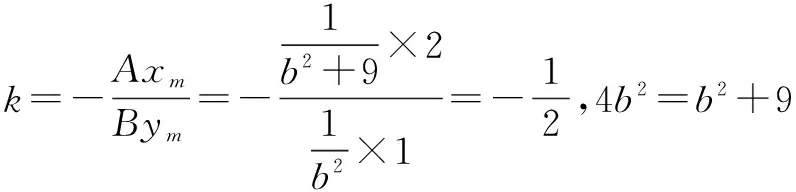
事实上，提炼结论并灵活运用是把常规方法中的很多繁琐而重复的过程加以省略.从而提高解题效率的一种有效做法，也是培养学生进行研究性学习并品尝研究成果的一种很好的方式.

G632

B

1008-0333(2017)01-0048-01