学会用“等时圆环模型”解答物理问题

湖南省岳阳县第一中学(414100)

卢小柱●

学会用“等时圆环模型”解答物理问题

湖南省岳阳县第一中学(414100)

卢小柱●

高中物理中有很多的经典模型，掌握这些模型对解题会带来很多方便，甚至省去很多麻烦，下面举例分析“等时圆环模型”.

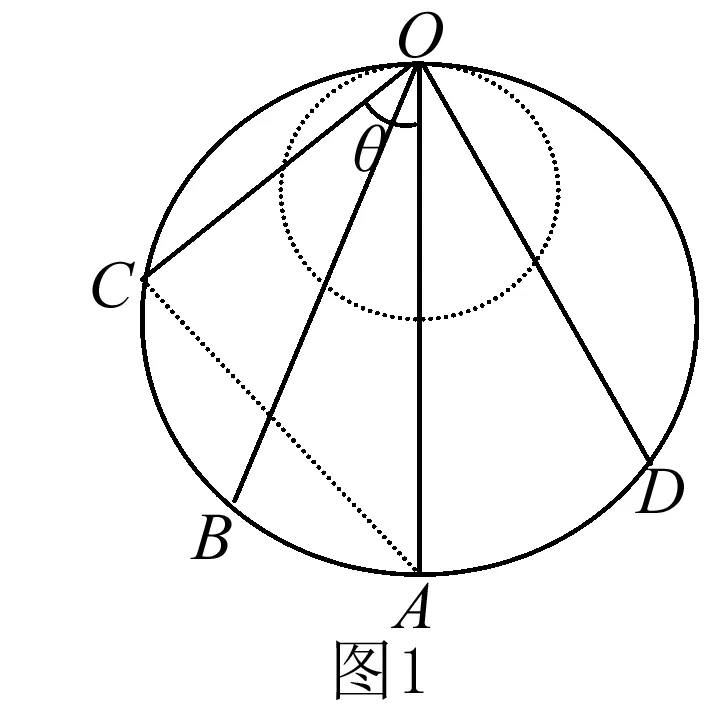
解题方法：抓住圆的半径相等，选取任意情况进行研究.比如物体从顶点O沿任意光滑轨道OC下滑，由图1可知，OC与竖直方向OA的夹角为，然后连CA，构成直角三角形.圆的半径为R，则下滑加速度为a=gcos，到达圆周上C点的位移为x=2Rcos，故到达C点的时间为

故下滑时间与轨道倾斜角度无关，从O点沿不同直轨道到达同一圆周上任意一点时间都相等.下面我们运动这一模型来解答物理问题.

例1 如图2所示，两光滑导轨靠在墙壁上固定不动，水平面上靠在同一点D处，另有一点C在D的正上方，已知CD=AC=H.现有三个光滑小球分别从A、B、C三点自由释放，则下列说法正确的是( ).

A.A球先到达D点；B、B球先到达D点；

C.C球先到达D点；D、三个球同时到达D点

解析 分析题意，我们作一个辅助圆如图3所示，圆心在C点.因为B点在圆周外，C点在圆周内，由上面的解题模型很快可以判断出C点最先到达D点，然后是A球，最后是B球.正确答案选C.

例2 如图4所示的斜面上分别有光滑轨道OA、OB，其中OA沿竖直方向，OB与斜面的夹角大于90，设一小球从O点沿OA、OB轨道运动到斜面上所用时间分别为tA、tB，则( ).

A.tA>tBB.tA

C.tA=tBD.无法确定

解析 如图5所示，作一辅助圆，O点为圆的顶点，则OA为圆的直径.过O作斜面的垂线OC，因为OB与斜面的夹角大于90，故B点在A、C之间，由上述模型可知，因为从O点到达A点和到达C点的时间相等，而B点在圆周内，所以到达B点的时间小于到达A点和C点的时间.正确答案选A.

例3 如图6所示，AB是一倾角为θ的输送带，P处为原料输入口，为避免粉尘飞扬，在P与AB输送带间建立一管道(假使光滑)，使原料从P处以最短的时间到达输送带上，则管道与竖直方向的夹角应为多大？

解析 借助“等时圆环”模型，可以过P点的竖直线为直径作辅助圆，要求该圆与输送带AB相切，如图7所示，C为切点，O为圆心.显然，沿着PC弦建立管道，原料从P处到达C点处的时间与比沿其它管道到达传送带上的时间短.因而，要使原料从P处到达输送带上所用时间最短，需沿着PC建立管道.根据题图条件，由几何关系可得：PC与竖直方向间的夹角等于θ/ 2.

根据上面分析，我们还可以在此基础上得到扩展性的结论：

扩展性结论①：如下图8所示，从O点沿不同光滑直轨道下滑的物体，它们任意时刻都在以O为顶点的同一圆周上.

扩展性结论②：物体从某点O沿不同方向、不同光滑直轨道由静止下滑时，任意时刻所在位置都在以该点O为顶点的同一球面上.

扩展性结论③：如图9所示，物体沿同一圆周上不同点由静止下滑，将同时到达最低点A.

G632

B

1008-0333(2017)01-0075-01