风力发电机轴承温度场研究

孙兴伟，张继伟

（沈阳工业大学 机械工程学院，沈阳 110870）

风力发电机轴承温度场研究

孙兴伟，张继伟

（沈阳工业大学 机械工程学院，沈阳 110870）

目前，风力发电迅速发展，发电机组可靠性非常重要，而分析发电机轴承温度变化可控制发电机工作性能。分析轴承温度场的研究方法主要有热网络法、有限元法及实验法。采用热网格法将发电机轴承系统温度节点离散化得到主要节点温度。利用传热学与摩擦学分析发电机轴承发热量数学模型，基于轴承工作状况，选择合适的轴承内部对流换热系数，在有限元软件下分析轴承内部稳态温度场的分布情况和热变形，得到了合理的轴承温度场云图，并分析了发电机轴承在风速突变转速下的温度场。

风力发电机；轴承；热网络法；有限元；温度场

0 引言

风力发电机是风能的主要利用方式，是把风能转换为电能的一种电气设备。全国滚动轴承标准化技术委员会也已制定了相关标准——JB/T10705-2007滚动轴承：风力发电机轴承。发电机轴承采用圆柱滚子轴承和深沟球轴承，要求高精度、低振动和低噪声[1]。

风力发电机组故障率偏高，在故障率中发电机轴承失效发生率较高，故障类型包括磨损失效、腐蚀失效、断裂失效、胶合失效等[2]。这些故障均与发电机温度场有关联，对发电机轴承温度场的变化研究可以对发电机组运行状况和故障情况。

国内外学者对轴承温度场的研究已经处于成熟阶段，比如陈观慈[3]采用混合编程的方法把拟静力学建立航空发动机高速轴承的力学模型与根据轴承的局部摩擦生热有机的结合起来，开发了高速球轴承与滚子轴承的热分析程序，并且利用轴承热分析软件所得到的结果与小型高速球与滚子轴承的台架实验所获得工作温度等相比差别在以里，证明了其设计的热程序符合预测高速轴承温度。只有郭艳伸[4]从理论上利用ANSYS解释风力发电机轴承正常运行状态下的温度场分布。因此对风力发电机轴承温度场分析可查阅的资料很少，因此可以尝试结合成熟的轴承温度场的分析方法与发电机轴承的自身特性利用有限元方法分析双馈风力发电机轴承温度场分布情况。

1 确定轴承内部发热量模型及计算模型

1.1 轴承发热量模型

研究风力发电机的轴承发热是首要的任务，其主要是由于轴承功率损耗，对于深沟球轴承而言，其主要因素有[5]：

1）球与内外滚道间的接触滑动摩擦。

（1）滑动摩擦方向为滚动体滚动方向（y方向是滚动方向，即球与滚道接触椭圆短轴）。

（2）滑动摩擦方向为滚动体滚动方向（x方向是垂直滚动方向，即球与滚道接触椭圆长轴）。

2）球与轴承内腔间的润滑摩擦生热。

3）球与保持架兜孔间接触滑动摩擦生热

4）保持架与内（外）引导挡边摩擦生热。

1.2 确定计算模型

在研究轴承发热量问题上，现已提出了三种发热量计算模型，即Palmgren发热量计算模型、Harris发热量计算模型、SKF发热量计算模型。基于10kw风力发电机中轴承的特殊性和工况特点，根据前述成熟的轴承发热量的计算，选择Palmgren发热量模型计算。

Palmgren轴承摩擦力矩是由两部分：载荷摩擦力矩Ml和粘性摩擦力矩Mv[6]。

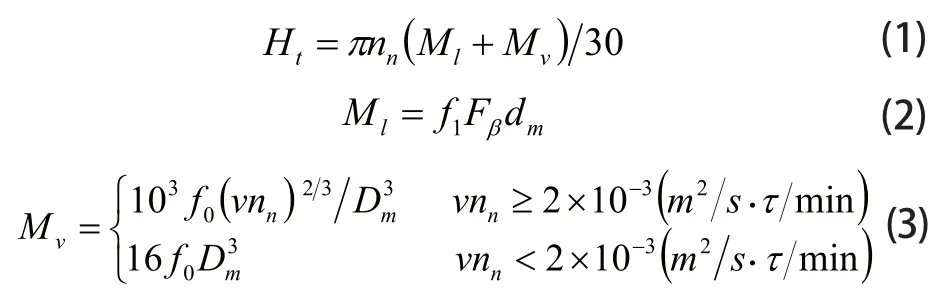
上式中，Ml，Mv的单位为N.m，nn为内圈的转速（r/min），ν为润滑油的运动粘度(m2/s)，Dm为轴承节圆直径（m）。Fr为轴承的径向载荷（N）。

1.3 对流换热系数

在分析轴承热传递过程中，是以导热、对流与辐射三种形式，其重点是研究轴承的对流换热模型。对流换热的牛顿公式为：

式中，Q为对流换热量，α为对流换热系数，A为换热面积，ΔT为对应轴承温度节点的温度差。虽然公式看起来很简单，但由于对流换热系数与材料的热物理性质与换热表面有很大的联系，故主要在换热系数很难确定。

对于深沟球轴承而言有两种对流换热模型：1）Rumbarger对流换热系数模型；2）Harris对流换热系数模型。根据风力发电机轴承的特性选择Harris对流换热系数模型。

空气自由对流换热系数[7]：

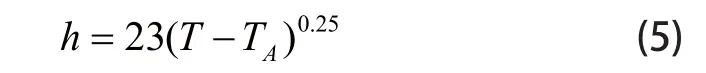
Harris[8]推荐轴承与润滑油等间对流换热系数为：

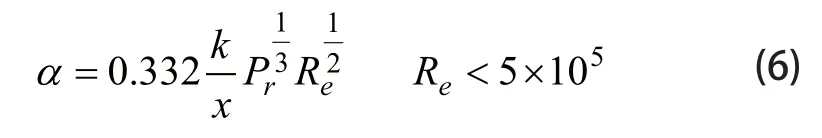
式中，k为润滑油的导热系数，Pr为润滑油的普朗特数，Re为雷诺数，为了方便计算发电机轴承的换热系数，这里的x取轴承座内直径。

2 等效热网格法分析轴承温度场

由于轴承内部滚动体排列的特殊性，因此采用经典的热传递方法无法求解轴承内部温度场，采用等效热网格法是以将整个轴承系统离散并不是以整体系统进行方程组求解，将轴承结构看作一组温度节点。对于在稳态温度场分布时，其中任意的节点中流入节点的热流等于流出节点的热流，也可以认为：对于轴承系统的每一个温度节点其热流的总和为零。流入节点的热流应该既包括本节点的因摩擦生热的功率损失和其他相关节点热传递所获得的热量[9]。

为了方便对发电机轴承热网格法分析温度场分布，故假定以下一些条件：

1） 如图1所示，假定9个温度节足以描述轴承系统，A为环境温度节点，T为润滑剂温度节点，其余7个节点温度需要确定。

2） 轴承座关于轴的中心线对称分布，不必考虑圆周方向的传热。

3） 为了简化计算，将轴承轴端温度默认为环境温度节点。

4） 轴承温度分布为一维热传递。

由于发电机轴承润滑为脂润滑，忽略热对流形式，只考虑热传导，轴承座与环境间热辐射量较少，只考虑对流形式。

球轴承温度节点布置与热传导系统如表1与表2所示，根据Burton和Steph[10]的研究，按照1：1的比例将摩擦生热量传入球与套圈间。

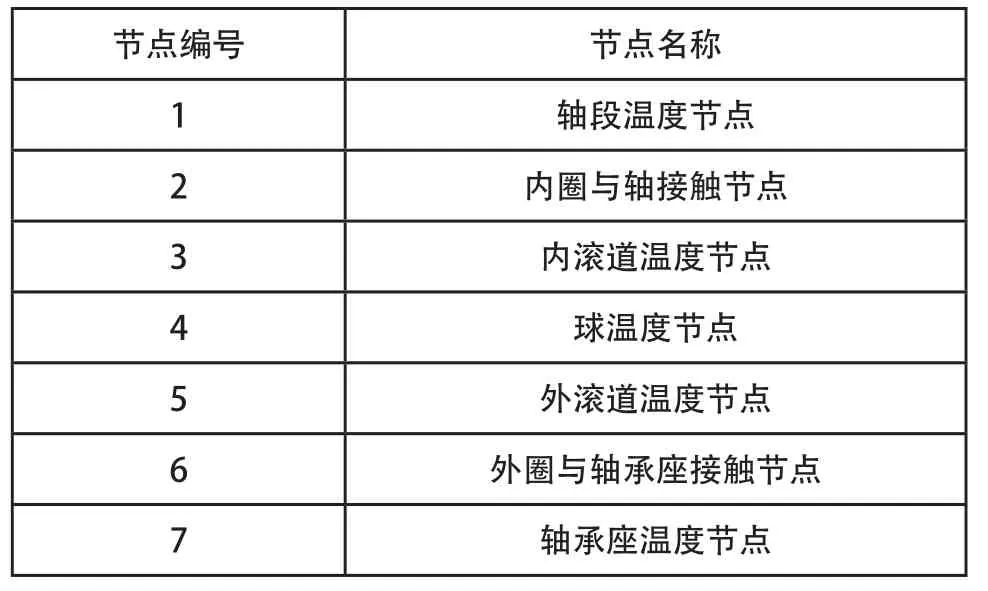
表1 轴承温度节点布置

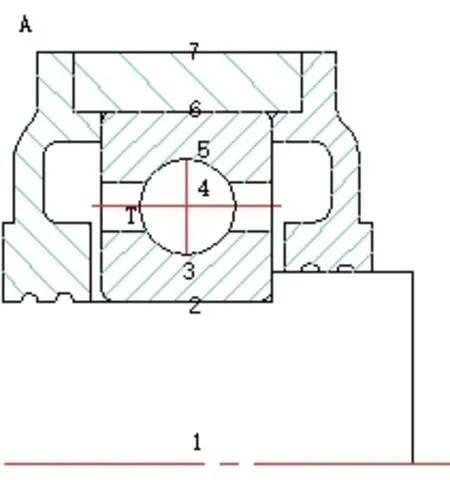
图1 轴承节点布置

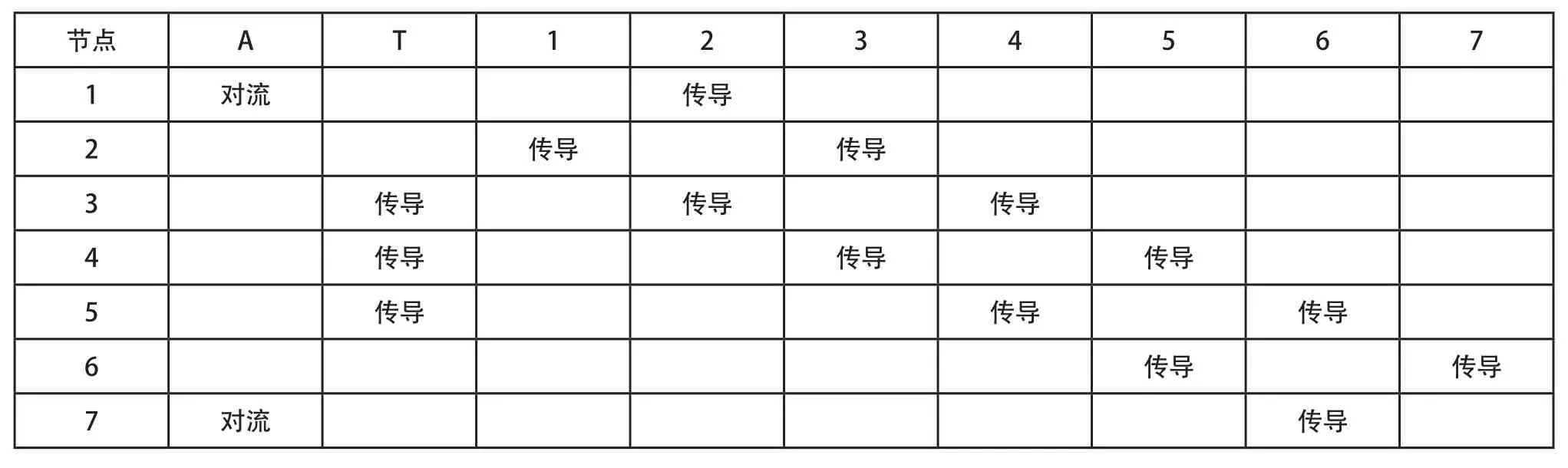
表2 温度节点对应的热传导系统

发电机轴承系统有9个温度节点，可以组成9个非线性方程组，利用Netwton-Raphson法求得温度节点。

3 正常状况下风力发电机轴承温度场分析

3.1 轴承有限元模型建立及网格划分

1） 有限元建模

对6311风力发电机轴承建模，其几何参数是：轴承外径是120mm，内径是55mm，宽度是29mm，球直径是11.3mm，球数目是8个，利用ANSYS中Workbench下的自带的建模工具Design-modeler建立的有限元模型，由于轴承的内外圈与滚动体间都有摩擦生热，且发电机轴承在高速运转下其内外滚道间产生的热量为周期性的，在分析计算时其工作量相当的大，不便于分析，同时为了加载热边界条件，因此需要对其简化，简化后的有限元模型如图2所示。

2） 材料属性设置

利用热模块分析时需要对轴承的材料进行属性设置，材料为GCR15轴承钢，密度为7890kg/m3，弹性模量取2.01Gpa，泊松比取0.3，比热容取450J/(kg.℃)，根据轴承的材料选择热导率为54(W/m.℃)[11]。

3） 网格划分

由于对风力发电机轴承进行温度场分析，采用有限元分析中常用的映射网格形式划分网格，考虑到热分析的准确性及热耦合间是直接耦合，故选择网格划分单元类型时必须全面包括温度场中的单元载荷，模型一共建立了16个接触对，减少计算的复杂程度并可以准备反映出发电机轴承温度场的情况，对轴承中的球体与沟道接触间局部细化，划分后的整体轴承网格如图3所示。

图2 轴承有限元模型

图3 轴承网格划分

3.2 设置边界条件

在对深沟球轴承发热量和轴承热对流形式研究的基础上，对发电机轴承加载热载荷和边界条件，在查阅国内外对轴承温度场分析的资料中，有学者提出了轴承温度场加载边界条件分析的三种模型，即：1）已知边界函数，知晓润滑油及界面温度，利用热网格法给出其余热温度条件；2）利用与轴承相接触的介质温度和对流换热系数知晓的介质热对流形式；3）由接触面间的摩擦生热作为热源给出的边界发热量。

为使有限元更好的反映轴承内部温度变化情况应保证球体与内外沟道间的接触摩擦系数，轴承材料的热导率等条件值是恒定值的前提下加载热边界条件。

对发电机轴承分析温度场的变化情况下的边界约束条件如下：

1） 发电机轴承的内外表面、球与外界的换热热对流系数由Harris换热公式确定；

2） 发电机轴承整体发热量由Palmgren发热量模型确定；

3） 将轴承发热量以热对流率的形式加载到球体和沟道接触的内、外面上；

4） 在发电机轴承内外圈以及球体的外表面上加载热对流；

5） 轴承外圈外表面施加全固定位移约束，内圈随着发电机轴旋转。

3.3 发电机轴承有限元结果分析

利用有限元分析软件的热分析模块求解发电机轴承稳态温度场的分布情况，假定环境温度为20℃，热源只考虑轴承自身摩擦发热，通过有限元方法对发电机轴承进行数值仿真，分析发电机在正常运行状态下的轴承温度场分布情况。图为在发电机在正常运行速度是1200r/ min轴承稳态温度场分布。

从图4轴承的整体发热量分布云图可知，发电机轴承在球体与内外滚道间接触的发热量最大，是轴承摩擦生热的主要来源。由于深沟球轴承在额定转速下运行中，滚动体与内外滚道间的接触会产生摩擦生热，球体在轴承内部运转，与外部的对流换热较小，其不易散热，所以球体的温度是最高的，为50.438℃，在整体发电机轴承运行过中，轴承的最高温度出现在于球体与内圈滚道接触的位置，而球与外圈滚道接触的位置的温度是，略低于内圈的温度，可知外圈的散热速度快。

图4 轴承温度场分布

3.4 结果分析

将通过有限元方法与热网格法分析轴承温度分布结果如表3所示。

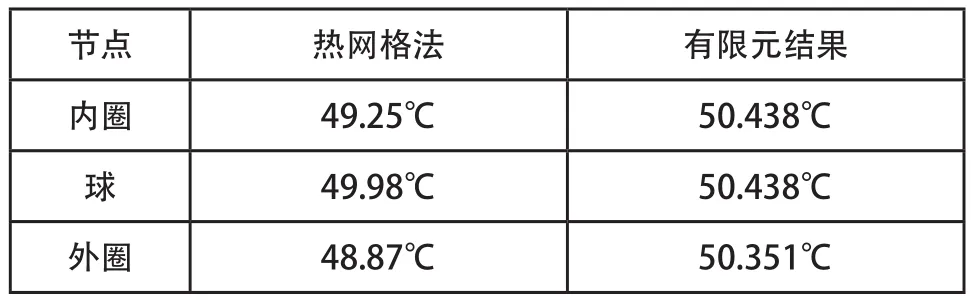
表3 计算结果对比

由表4可知，利用有限元分析其轴承温度场计算结果大，因为相比于热网格法的二维温度场分析，有限元方法是三维方法，在建模过程中，只考虑了轴承，并没有将轴承、轴承座、轴三者有机的联系起来，没有考虑其中的热传导过程，而利用热网格法考虑了所有的热传导过程。在有限元方法与一家厂家在试验过程所提供的轴承温度数据相比，厂家提供的轴承平均温度变化是50.55℃，相差不大。

4 发电机轴承热变形研究

4.1 热-应力耦合下有限元分析步骤

1）建立发电机轴承接触分析有限元模型；

2）定义材料的属性，即轴承钢的密度、热热导率、弹性模量、泊松比及比热容等，前节中已经定义了轴承的材料属性；

3）网格划分及定义轴承接触类型，本节定义的轴承接触类型是非线性接触；

4）选择轴承稳态热分析，加载边界条件，得到发电机轴承稳态温度场分布；

5）将得到的发电机轴承稳态分布加载到静力学；

6）加载轴承初始温度与边界约束条件，分析热载荷作用下的热机耦合[12]。

将前节中的轴承稳态热分析导入到有限元静力学分析中如图5所示。

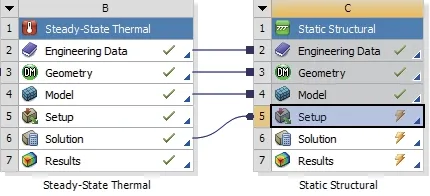
图5 热应力耦合有限元模块

4.2 有限元结果分析

根据双馈风力发电机轴承的安装与运行的实际情况，采用以下约束条件：

1）模拟轴承外圈与轴承座相配合，固定轴承外圈；

2）模拟轴承内圈的旋转速度，施加转速为1200r/ min，施加径向载荷Fr=2000N，轴承的工作环境温度是50℃；

利用有限元软件对发电机轴承的接触分析得到的轴承的接触应力云图与径向变形云图是图6～图8。可以从图6～图8得到，加载热载荷后的最大的热应力耦合是26.055MPa，最大热应力耦合径向变形是13.353μ m。图中可知，由于发电机轴承中的球体的温度最高，轴承在运行状态下由于温度的变化而引起各部分热应力的变化，但最大热应力与最大接触应力的位置仍为最大径向载荷加载在滚动体与内圈接触位置处。表4中反映了在同样条件下的加载热载荷与结构静力学分析得到的相比较。

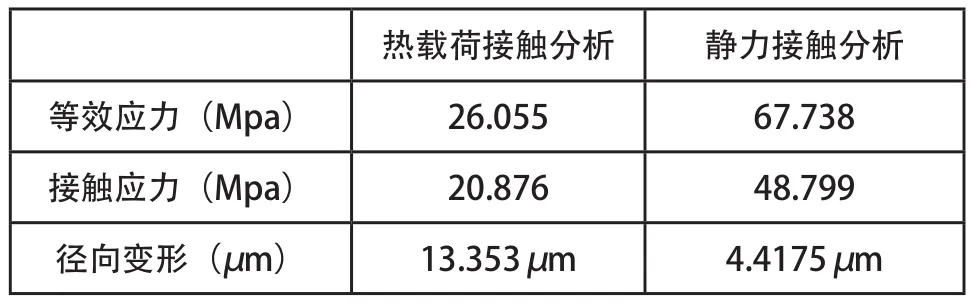
表4 结果对比分析

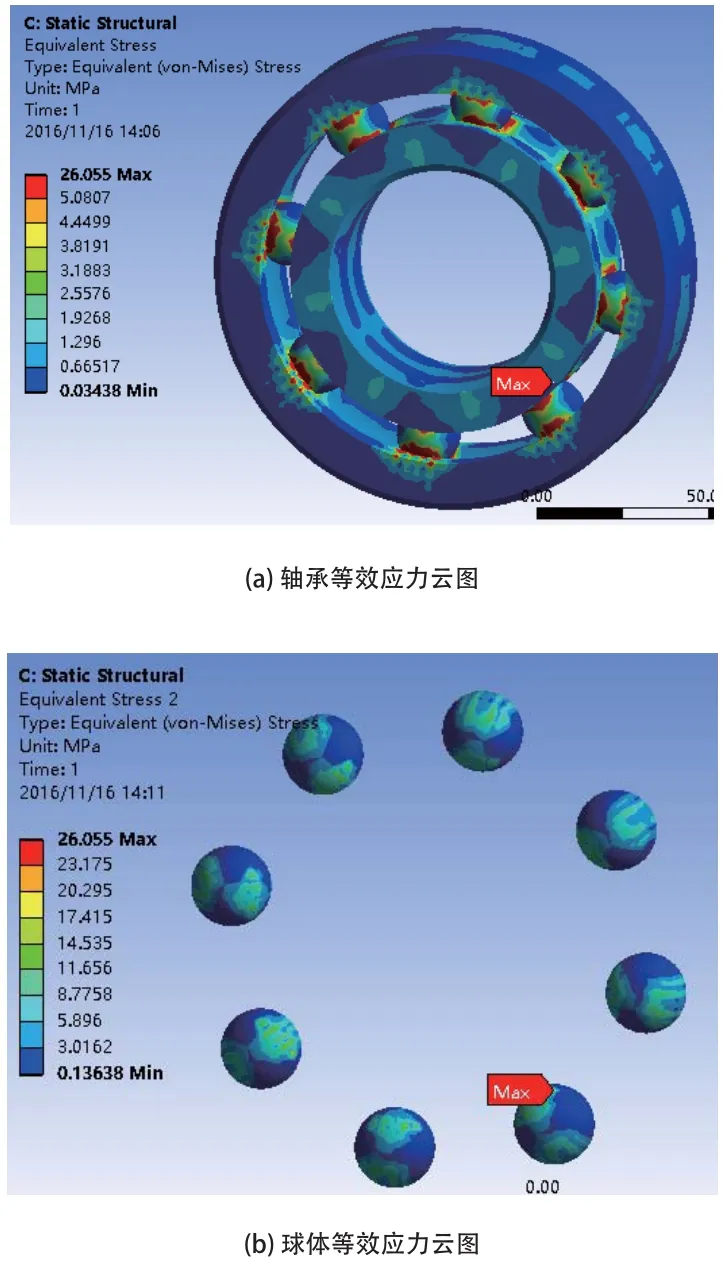
图6 加载温度场后轴承等效应力云图

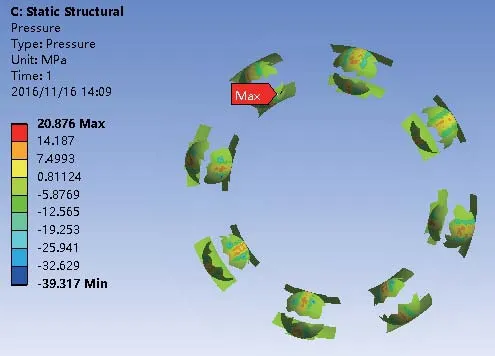
图7 加载温度场后轴承接触应力云图

图8 加载温度场后轴承径向变形云图

表4是发电机轴承考虑温度场下的前后有限元分析对比结果，由于在发电机轴承加载温度场后，其接触应力与径向变形都有一定程度的变化，其中，加载热载荷后接触应力变小，径向变形增大，原因在于由于增加了轴承的热载荷后，轴承受热膨胀，增加了轴承球体与内外沟道间的接触面积，从而使接触力变小，径向变形有所变大。

5 非正常工作条件下的发电机轴承温度场分析

在风力发电机开始在10kw下正常运行状态轴承会产生稳定的温度场，上述已经分析完成轴承稳定热分析，由贝兹理论[13]知，风速v的三次方与风力发电机功率P成正比关系，随着风速的不断上升，风机叶片的转速也会随着升高，功率也会随着变化升高，利用有限元分析对风速在1500r/min时发电机轴承的温度场情况。

从图9中可以看出，相比于风速在额定状态下运行的风力发电机轴承的稳态温度场，在风速为1500r/min轴承的最高温度变成了92.695℃，超过了10kw风力发电机组轴承运行环境85℃，对轴承健康运行十分不利，会发生轴承胶合等损失，缩短轴承的使用寿命，不利于风力发电机组运行。因此风力发电机组不应安在风速变化的场合或功率突变场合下工作。

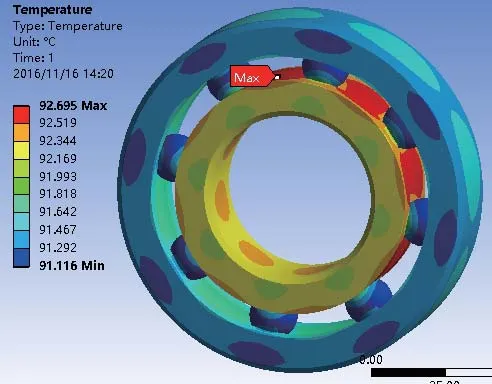
图9 风速突变轴承温度场云图

6 结论

1）风力发电机轴承在内部的摩擦生热主要是以两种形式散发即以热传导和对流换热，而对于热传递的第三种方式热辐射由于轴承内部的温度差相差不是很大，因此在考虑轴承摩擦生热热传递时可以不予考虑；

2）通过ANSYS Workbench建立10kw风力发电机轴承正常运行与风速突变下的工况条件下分析温度场变化情况，并将正常工作下的与等效热网格法得到轴承温度比较，利用有限元软件得到的温度比网格法得到的温度均高，与厂家所提供的轴承温度变化数据相差不多，应在实际中较充分的利用两种方法分析风电机轴承温度；

3）由于风力发电机的安装位置通常为40m～60m的高空中，再由于其轴承制作的特殊性，不便利用红外测量仪等机器对轴承的温度进行测量，利用有限元方法对发电机轴承的温度场研究有重要的意义，可以整体了解发电机轴承的运行状态并判断发电机的发热情况和对风力发电机组优化设计。

[1] JB/T 10705-2007.滚动轴承风力发电机轴承[S].

[2] 周方明.基于分形分析的轴承故障状态分类研究[D].合肥：中国科学技术大学,2011.

[3] 陈观慈.航空发动机主轴高速滚动轴承热分析[D].哈尔滨：哈尔滨工业大学,2008.

[4] 郭艳伸,常喜强,等.基于ANSYS的风力机组发电机轴承热分析[J].四川电力技术,2016,39(4)：6-10.

[5] T.A.Harris,M.N.Kotzalas.滚动轴承分析(原书第五版)：第2卷,轴承技术的高等概念[M].北京：机械工业出版社,2009.

[6] 刘志全,张永红,苏华.高速滚动轴承热分析[J].润滑与密封,1998(4)：66-68.

[7] 杨世铭,陶文铨.传热学[M].北京：高等教育出版社,2006.

[8] Harris T A.Rolling Bearing Analysis[M].3nd.John wiley and sons Inc.1990.

[9] 陈观慈,王黎钦,郑德志.高速球轴承的生热分析[J].航空动力学报,2007,22(1)：163-168.

[10] Burton R A,Steph H E.Thermally Activated seizure of angular Contact Bearing[J].ASLE Trans,10：408-417,1967.

[11] 《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京：机械工业出版社,1995.

[12] 黄志新,刘成柱.ANSYS Workbench 14.0 超级学习手册[M].北京：人民邮电出版社,2013.

[13] 周双喜,鲁宗相.风力发电与电力系统[M].北京：中国电力出版社,2011.

Research on bearing temperature fi eld of wind turbine generator

SUN Xing-wei, ZHANG Ji-wei

TM14

：A

：1009-0134(2017)05-0078-06

2016-12-14

国家自然科学基金重点项目（51537007）；辽宁省科技创新重大专项（201303005）

孙兴伟（1970 -），女，辽宁人，教授，博士，研究方向为复杂曲面制造技术及专用数控机床开发、大型能源装备研发等。