碳纤维增强复合材料加固中心孔钢板综合优化

伍希志 程军圣

1.中南林业科技大学交通运输与物流学院，长沙,4100822.湖南大学汽车车身先进设计制造国家重点实验室，长沙,410082



碳纤维增强复合材料加固中心孔钢板综合优化

伍希志1程军圣2

1.中南林业科技大学交通运输与物流学院，长沙,4100822.湖南大学汽车车身先进设计制造国家重点实验室，长沙,410082

采用多级优化方法对碳纤维增强复合材料加固中心孔钢板进行优化设计，首先，采用拉丁超立方方法选取试验样本点，利用移动最小二乘法拟合近似代理模型，在代理模型基础上采用自适应响应面优化方法优化基本铺层厚度；然后，结合复合材料制造约束条件，利用Optistruct对铺层顺序进行优化，得到最佳铺层设计方案。经过多级优化设计后，钢板中心孔处应力分布更合理，最大Mises应力减小了56.6%。

碳纤维增强复合材料；拉丁超立方；移动最小二乘法；自适应响应面；铺层顺序优化

0 引言

碳纤维增强复合材料(carbon fiber reinforced polymer,CFRP)具有比强度和比刚度高、可设计性好、防腐蚀等优点，在裂纹结构修复中已得到广泛研究和应用[1-4]。伍希志等[5]采用止裂孔和CFRP加固联合方法修复裂纹钢板，不仅减小了缺口钢板的名义应力，而且降低了疲劳缺口敏感度，使得疲劳寿命比缺口钢板疲劳寿命提高292倍。对于简单单向拉伸裂纹钢板的修复，复合材料铺层设计比较容易确定，而实际结构中钢板的受力方向是多向的，对于受力复杂的裂纹钢板的修复，复合材料层合板的铺层设计非常复杂。目前国内外已有学者对复合材料铺层优化进行了研究，如修英姝等[6]、TUAN等[7]、NAN等[8]分别采用神经网络法确定复合材料层合板规定角度下的铺层数,并采用遗传算法优化这种铺层结构下的铺层顺序。唐文艳等[9]、ALMEIDA等[10]、金达锋等[11]以临界屈曲载荷最大为目标，采用遗传算法对复合材料层合板的铺层顺序进行了优化设计。这些方法具有全局收敛、无需可微性等优点，但在结构优化中需要迭代多次，每次迭代都需要调用有限元计算，使得优化效率较低[12]。本文采用多级优化方法对CFRP加固中心孔钢板进行优化设计：首先采用移动最小二乘法(moving least squares)拟合钢板中心孔最大Mises应力的近似代理模型，在代理模型基础上采用自适应响应面优化方法(adaptive response surface method,ARSM)优化复合材料的基本铺层厚度，优化过程中不需要进行有限元计算，提高了优化效率；然后利用Optistruct对铺层顺序进行优化，得到最佳铺层设计方案。

1 问题提出

由于复合材料层合板具有各向异性，即纤维方向的弹性模量和强度远大于横向的弹性模量和强度，因此在复合材料加固中心孔钢板中，为了获得更好的修复效果，需要对复合材料铺层进行优化设计，包括基本铺层的铺层厚度和铺层顺序。

基本铺层的铺层厚度优化是以基本铺层的铺层厚度为设计变量，在满足钢板中心孔处最大Mises应力σ0约束条件下使复合材料总厚度最小。设T={t1，t2，…，tn},ti(i=1,2,…,n)为基本铺层i的铺层厚度，则铺层厚度优化问题的数学模型可表示为

(1)

式中，f(X)为钢板中心孔处最大Mises应力；t为复合材料总厚度;ai为单层最大厚度。

铺层顺序优化的数学模型可表示为

(2)式中，f(Y)为钢板中心孔处最大Mises应力；gi(Y)为铺层约束条件；Y为各铺层的排列；A为所有铺层排列的集合。

2 优化算法

针对CFRP加固中心孔钢板的铺层优化问题，本文采用一种多级优化方法来优化铺层厚度和铺层顺序，优化流程如图1所示，首先利用ABAQUS建立CFRP加固中心孔钢板的有限元参数模型；然后依据拉丁超立方方法(Latin hpercube)设计参数样本点，代入样本参数进行有限元计算，根据样本模型计算结果，利用移动最小二乘法进行响应面拟合，得到钢板中心孔处最大Mises应力的代理模型,再在代理模型基础上采用自适应响应面优化方法对复合材料基本铺层厚度进行优化(一级优化)，此时无需进行有限元计算便可得到最佳的铺层厚度参数；最后结合复合材料制造约束条件，利用Optistruct对铺层顺序进行优化(二级优化)，得到最终铺层设计方案。

图1 多级优化流程图Fig.1 Multi-level optimization flow chart

2.1 移动最小二乘法

传统的响应面近似模型一般使用最小二乘法进行拟合，它是根据误差平方和最小得到一个线性方程组，从而求解待定系数。最小二乘法拟合的计算过程比较简单，但当拟合复杂形状的响应面时，拟合精度比较差，而采用移动最小二乘法拟合就可以解决上述问题。

移动最小二乘拟合函数u(x)是由系数矢量a(x)和基函数P(x)构成，同时它认为点x处的函数值u(x)只受x附近区域Ωx内点的影响，Ωx外的点对u(x)没有影响，这个区域Ωx称为点x的影响域。在点x处的近似函数u(x)可以表示为[13]

(3)

PT(x)=(p1(x),p2(x),…,pm(x))

a(x)=(a1(x),a2(x),…,am(x))T

式中，PT(x)为基函数向量；m为基函数个数；a(x)为待定系数。

常用的二维空间中的二次基函数为

在移动最小二乘法拟合中，系数a(x)是通过在点x的邻域Ωx内的近似函数u(x)与函数值y(x)的误差加权平方和最小来确定的，即

(4)

pj(xi)=0

(5)

其中，n为点x的邻域Ωx内包含的采样点数，ω(xi)为节点xi的权函数，工程中常采样高斯权函数，即

(6)

式中，r为影响域相对半径大小;β为参数。

2.2 自适应响应面优化法

自适应响应面优化法(ARSM)的基本思想是先通过较少的样本点构造一阶响应面，确定优化方向，然后在梯度方向以适当步长获取新设计点，并引入新设计点来重构响应面，这样便可以比较准确且快速地找到最优点。

在自适应响应面法中，约束函数和目标函数都可以用以下二阶多项式进行拟合：

j=1，2,…，m+1

(7)

式中,aj0、aji、ajik为二次多项式系数。

具体优化过程如下：

(1)计算初始点和扰动设计变量产生的n个设计点。

(2)利用最小二乘法计算目标函数和约束函数的多项式系数。如果设计点数为n+1，可以确定常数项和一次项系数；随着设计点数增加，二次项系数逐渐确定；当设计点数大于1+n+(n+1)·n/2时，可通过加权来计算二次项系数。

(3)利用数学规划法对响应面进行优化求解，如果优化迭代结果已经收敛，则终止迭代；反之，返回步骤(2)继续迭代计算。

2.3 铺层顺序优化

由于复合材料铺层顺序对复合材料结构的力学性能和工艺性能存在重要影响，所以在复合材料优化设计中，铺层顺序优化是必不可少的环节。本文铺层顺序优化采用Optistruct的composite shuffle 模块。

从力学和工艺性能考虑，复合材料铺层设计一般遵循以下原则[14]：①铺层纤维轴向应尽量与所受载荷方向一致，以便利用纤维轴向高强度和高刚度的特点；②同一方向铺层连续铺层数量不得大于4；③铺层纤维方向通常为0°、90°和±45°；④为了避免树脂直接承载，应同时包含0°、90°和±45°四种铺层。

3 优化算例

3.1 建立有限元模型

CFRP加固中心孔钢板的有限元模型如图2所示，钢板长450 mm、宽400 mm、厚3 mm，中心有直径10 mm的圆孔，材料是304不锈钢，屈服强度σs为310 MPa；在圆孔处单面粘贴总厚度为4 mm的CFRP，CFRP由0°、90°和±45°基本铺层组成，每种基本铺层厚度为1 mm，胶层厚度为0.3 mm。钢板和CFRP采用四节点减缩积分四边形壳单元S4R模拟，胶层采用八节点粘贴单元COH3D8模拟，总共单元数量为7866，节点数量为6671。边界条件是约束钢板四边节点的三个移动自由度，在钢板上施加均匀压力载荷0.02 MPa。

图2 CFRP加固中心孔钢板的有限元模型Fig.2 Finite element model of CFRP reinforcing center hole steel plate

碳纤维布采用东丽公司生产的CUDP-H150/T700-E7型碳纤维布，其性能指标列于表1。胶层材料采用西卡Sikadur-330树脂，属性详见文献[15]。

表1 试验碳纤维布的性能

假定每个CFRP基本铺层厚度为1 mm，铺层纤维方向为±45°,基本铺层必须相邻，分析基本铺层顺序对钢板圆孔处最大Mises应力的影响，结果如表2所示。从表2中可以发现，基本铺层顺序为±45°/0°/90°时，钢板圆孔处最大Mises应力最小，因此后续分析模型以±45°/0°/90°为基本铺层顺序。

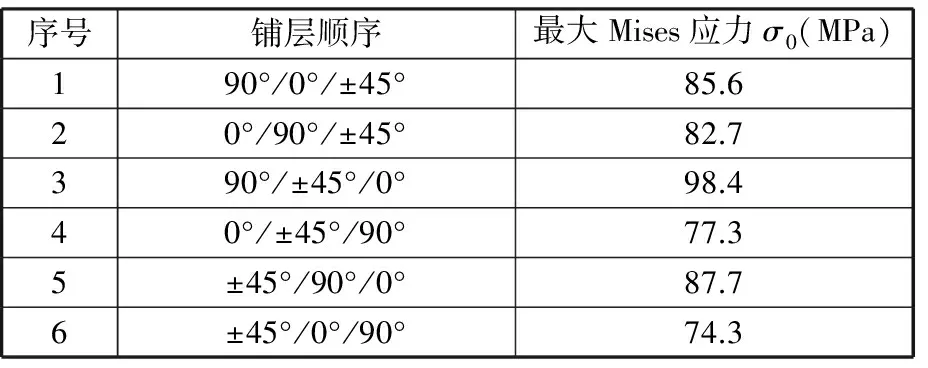
表2 基本铺层顺序对钢板圆孔处最大Mises应力的影响

3.2 建立响应面近似模型

建立响应面近似模型需要一系列具有代表性的仿真数据点，这些仿真数据点的分布会影响近似响应面的拟合精度，因此需要合理地布置数据点。本文采用拉丁超立方(Latin hypercube)方法进行试验设计，为近似响应面模型提供初始数据点。设计变量为基本铺层0°、90°和±45°的厚度(±45°的厚度相等)，近似函数为钢板中心孔处最大Mises应力，总共30个数据点，拉丁超立方生成的设计变量空间如图3所示。

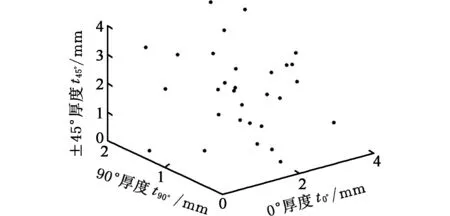
图3 拉丁超立方生成的设计变量空间Fig.3 Design variable space generated by Latin hypercube

根据拉丁超立方试验计算结果，利用移动最小二乘法拟合钢板中心孔处最大Mises应力的近似模型。移动最小二乘法的基函数为二次基函数，权函数为高斯权函数，拟合计算结果如图4所示。从图4可以看出，钢板中心孔处最大Mises应力的拟合值与仿真值非常吻合，各个数据点的相对误差基本都小于1%，平均相对误差为0.19%。

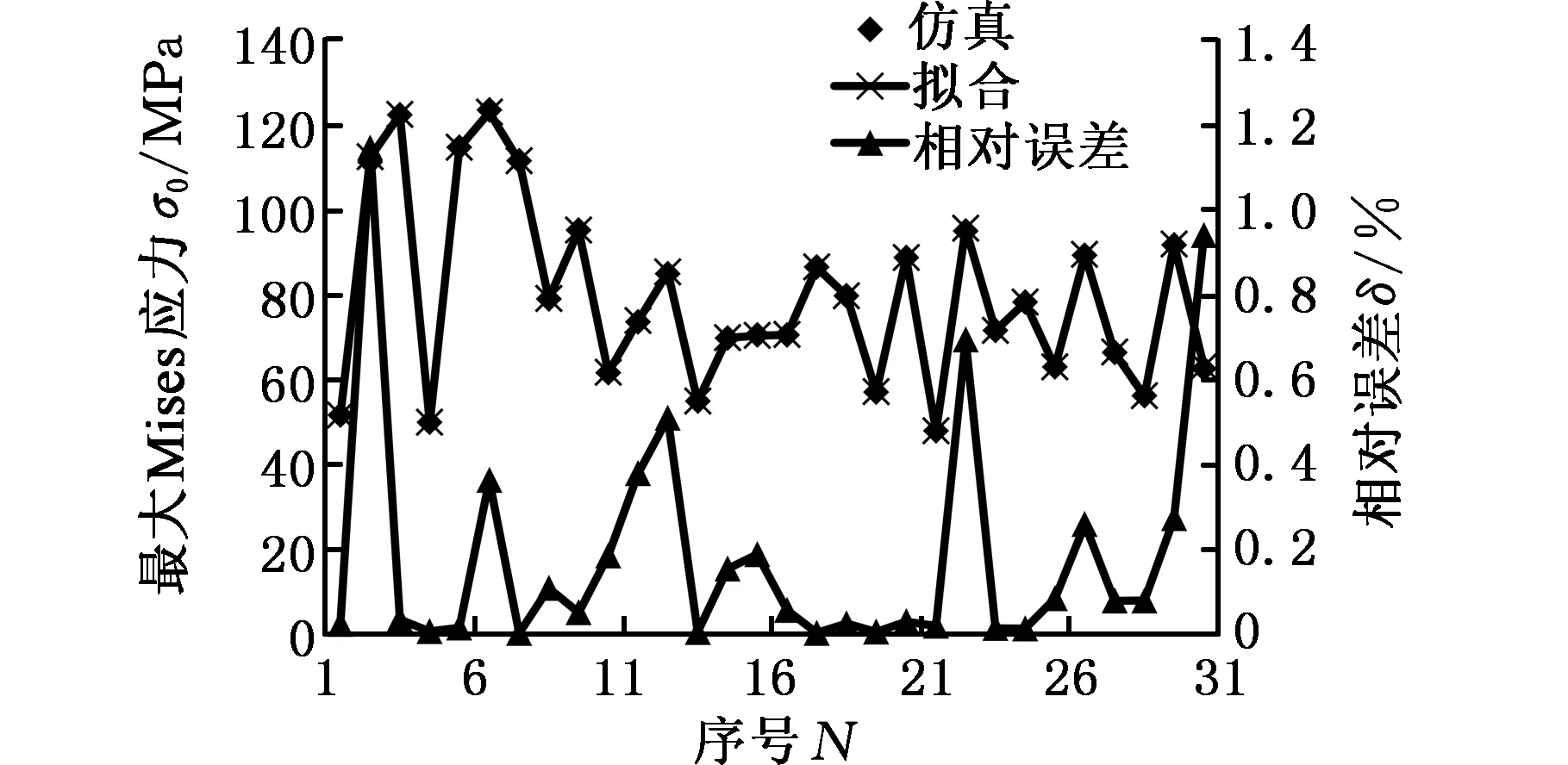
图4 仿真值与拟合值对比Fig.4 Comparison of simulation and fitting value

移动最小二乘和传统最小二乘拟合相对误差对比如图5所示，两者采用相同的数据点，传统最小二乘拟合为二次多项式。从图5中可以看出，移动最小二乘拟合的相对误差明显比传统最小二乘拟合误差小，传统最小二乘拟合的平均相对误差为1.10%，而移动最小二乘拟合的平均相对误差为0.2%。

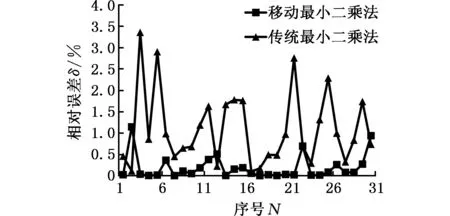
图5 移动最小二乘和传统最小二乘拟合相对误差对比Fig.5 Relative error comparison of moving least squares and traditional least-squares fitting

3.3 自适应响应面优化

根据移动最小二乘法拟合的代理模型，采用自适应响应面法对复合材料基本铺层厚度进行优化设计，优化迭代时不需要进行有限元计算。设计变量的设置如表3所示。以钢板中心孔处最大Mises应力小于70 MPa为约束条件，复合材料总厚度最小为优化目标进行优化计算，经过24步迭代，得到如表3所示优化结果。从表3中可以看出，复合材料总厚度为4.395 mm，钢板中心孔处最大Mises应力为70.003 MPa，满足约束条件。

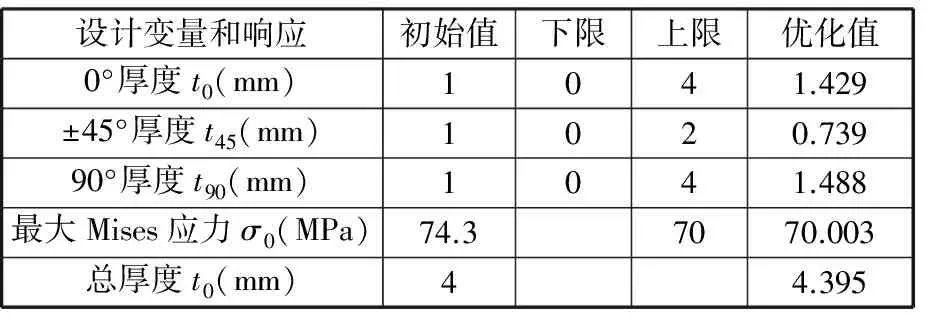
表3 设计变量和响应的初始值和优化值

3.4 铺层顺序优化

对于CFRP层合板，所有基本铺层的单层厚度均相等，单层CFRP厚度为0.125 mm。根据第一步尺寸优化结果，采用下面公式可以计算出第i个基本铺层的铺层层数：

Ni=8xi

(8)

由尺寸优化结果和式(8)计算出的各基本铺层的铺层数量如表4所示。假设初始铺层顺序为[(45°/-45°)6/0°12/90°12]，采用Optistruct的composite shuffle 模块进行优化，以钢板中心孔处最大Mises应力最小为优化目标，设置制造约束条件为连续铺层数量不大于4层，45°铺层必须成对排列。经过7步迭代后，最终优化后的铺层顺序为：[(45°/-45°)4/0°2/(45°/-45°)2/0°4/90°2/0°2/90°4/0°2/90°4/0°2/90°2]。

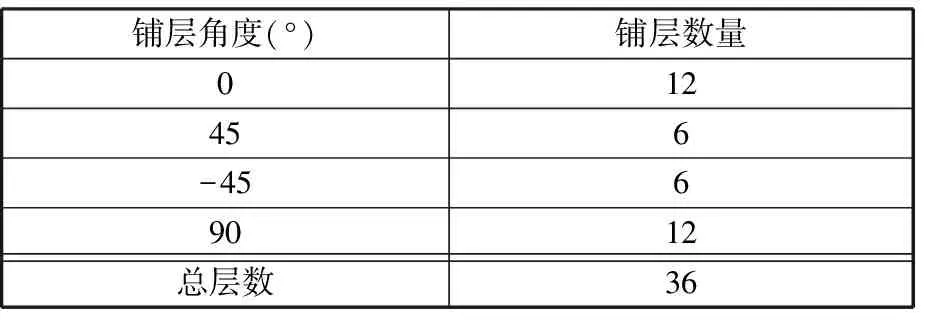
表4 基本铺层的铺层数量

CFRP加固前后钢板中心孔局部Mises应力如图6所示，从图中可以看出，未经CFRP加固的钢板，中心孔处左右两边的Mises应力比上下两边大，最大Mises应力为157.7 MPa，位于中心孔的左右边缘；CFRP加固后的钢板，中心孔边缘的Mises应力基本相等，最大Mises应力为68.50 MPa。

(a)加固前

(b)加固后图6 CFRP加固前后钢板中心孔局部Mises应力Fig.6 Mises stress of before and after CFRP reinforcing center hole steel plate

因此，经过CFRP加固优化设计后，钢板中心孔处应力分布更合理，最大Mises应力减小了56.6%。

4 结论

(1)采用多级优化方法对CFRP加固中心孔钢板进行了优化设计。整个优化过程仅需试验设计和铺层顺序优化时进行有限元计算，提高了优化效率；优化设计后钢板中心孔处应力分布更均匀，最大Mises应力减小了56.6%。

(2)传统最小二乘拟合法的平均相对误差为1.10%，而移动最小二乘拟合法的平均相对误差为0.2%，明显比传统最小二乘拟合法小。

[1] 郑云，叶列平，岳清瑞，等. CFRP板加固含裂纹受拉钢板的疲劳性能研究[J].工程力学，2007，24(6)：91-97. ZHENG Yun, YE Lieping, YUE Qingrui, et al. Study on Fatigue Behavior of Cracked Tensile Steel Plates Reinforced with CFRP Plates[J]. Engineering Mechanics,2007,24(6)：91-97.

[2] COLOMBI P，BASSETTI A，NUSSBAUMER A. Analysis of Cracked Steel Members Reinforced by Pre-stress Composite Patch[J]. Fatigue Fract. Eng. Mater. Struct.，2003,26:59-66.

[3] TIEN C, YU B, ZHAO X L. Mechanical Characterization of Steel/CFRP Double Strap Joints at Elevated Temperatures[J]. Composite Structures,2011,93(2):1604-1612.

[4] JONES S C，CIVJAN S A. Application of Fiber Reinforced Polymer Overlays to Extend Steel Fatigue Life[J]. Journal of Composites for Construction，2003,7(4):331-338.

[5] 伍希志，林彬，程军圣. 裂纹钢板的止裂孔与CFRP加固及其疲劳寿命预测研究[J]．天津大学学报，2016,35(4):637-648. WU Xizhi, LIN Bin, CHENG Junsheng. Study on Cracked Steel Plates Repaired by Stop Holes and CFRP and Fatigue Life Prediction[J]. Journal of Tianjin University,2016,35(4):637-648.

[6] 修英姝，崔德刚. 复合材料层合板稳定性的铺层优化设计[J].工程力学，2005,22(6)：212-216. XIU Yingshu, CUI Degang. Ply Optimization Design for Stability of Composite Laminates[J]. Engineering Mechanics，2005,22(6)：212-216.

[7] TUAN L M. JAE H L. Stacking Sequense Optimization for Maximum Strengths of Laminated Composite Plates Using Genetic Algorithm and Isogeometric Analysis[J]. Composite Structures,2014,116:357-363.

[8] NAN C, WANG W, YANG W, et al. Ply Stacking Sequence Optimization of Composite Laminate by Permutation Discrete Particle Swarm Optimization [J]. Structural and Multidisciplinary Optimization,2010,41(2):179-187.

[9] 唐文艳, 顾元宪, 赵国忠. 复合材料层合板铺层顺序优化遗传算法[J]. 大连理工大学学报，2004，44(2):186-189. TANG Wenyan, GU Yuanxian, ZHAO Guozhong. Stacking Sequence Optimization of Composite Laminate Plates by Genetic Algorithm[J]. Journal of Dalian University of Technology，2004，44(2):186-189.

[10] ALMEIDA F S , AWRUCH A M. Design Optimization of Composite Laminated Structures Using Genetic Algorithms and Finite Element Analysis[J]. Composite Structures,2009,88(3):443-454.

[11] 金达锋, 刘哲, 范志瑞. 基于遗传算法的复合材料层合板削层结构铺层优化[J].复合材料学报, 2015,32(1):236-242. JIN Dafeng, LIU Zhe, FAN Zhirui. Ply Optimization of Composite Laminate with Ply Drop Based on Genetic Algorithm[J]. Acta Materiae Compositae Sinica,2015,32(1):236-242.

[12] 张勇,李光耀,钟志华.基于移动最小二乘响应面方法的整车轻量化设计优化[J].机械工程学报, 2008,44(11):192-196.

ZHANG Yong, LI Guangyao, ZHONG Zhihua. Design Optimation Lightweight of Full Vehicle Based on Moving Least Square Response Surface Method[J]. Journal of Mechanical Engineering,2008,44(11):192-196.

[13] 杨建军, 郑健龙. 移动最小二乘法的近似稳定性[J].应用数学学报, 2012,35(4):637-648. YANG Jianjun, ZHENG Jianlong. Stability of Moving Least Squares Approximation[J]. Mathematicae Applicatae Sinica,2012,35(4):637-648.

[14] 中国航空航天研究院. 复合材料结构设计手册[M]. 北京: 航空工业出版社,2004. Chinese Aeronautics and Astronautics. Composite Material Structure Design Manual[M]. Beijing: Aviation Industry Press,2004.

[15] 伍希志，任会礼，钟懿.基于粘聚力理论的CFRP加固钢板剥离机理研究[J].固体力学学报，2015，36(6)：197-203. WU Xizhi, REN Huili, ZHONG Yi. Theoretical and Experimental Study on Debonding Mechanism of Steel Plate Strengthened with CFRP[J]. Chinese Journal of Solid Mechanics,2015,36(6)：197-203.

(编辑 王艳丽)

Optimization of Carbon Fiber Reinforced Polymer Reinforcing Center Hole Steel Plates

WU Xizhi1CHENG Junsheng2

1.College of Transportation and Logistics, Central South University of Forestry and Technology, Changsha,410082 2.Stake Key Laboratory of Aduanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha,410082

A multi-stage optimization method was adopted for carbon fiber reinforced polymer reinforcing center hole steel plate. The method was divided into two steps: firstly, sample points were selected based on the Latin hypercube method, an agent model was fitted by the moving least square, and the thickness of basic laminate was optimized based on the adaptive response surface optimization method. Secondly, considering composite’s manufacturing constraints, the stacking sequence was optimized by use of Optistruct software to obtain optimum design. Through the multi-stage optimization design, the stress of center hole steel plate is distributed more reasonable, and the maximum Mises stress is reduced by 56.6%.

carbon fiber reinforced polymer; Latin hypercube; moving least square; adaptive response surface method; stacking sequence optimization

2016-06-23

国家高技术研究发展计划(863计划)资助项目(2013AA040203)；国家自然科学基金资助项目(51305045)；中国博士后科学基金资助项目(2014M562099)；智能型新能源汽车国家2011协同创新中心资助项目；湖南省绿色汽车2011协同创新中心资助项目

TB33

10.3969/j.issn.1004-132X.2017.11.008

伍希志，男,1985年生。中南林业科技大学机电学院讲师。研究方向为结构优化、复合材料加固技术、机器人技术。发表论文7篇。E-mail:wuxizhi2006@126.com。程军圣，男，1967年。湖南大学机械运载与车辆工程学院教授。