太阳同步回归轨道卫星的重访特性研究
贾向华,徐 明
(北京航空航天大学 宇航学院, 北京 100191)
【基础理论与应用研究】
太阳同步回归轨道卫星的重访特性研究
贾向华,徐 明
(北京航空航天大学 宇航学院, 北京 100191)
针对太阳同步回归轨道的重访问题,提出了探究重访特性的系统方法。该方法以Q值建立太阳同步与回归轨道间的联系;采用基本交点距的描述方法,将回归周期内轨道的访问顺序加以量化;应用数论中的贝祖定理,将重访周期的确定转换为求解一丢番图代数方程。仿真算例选以光学载荷对地观测为前提,得到了特定回归周期轨道的访问顺序及地面覆盖情况,确定了相应的重访特性;此外,以轨道高度范围为约束,以快速重访为目标,确定了太阳同步回归轨道的设计方法。结果表明,该方法可以确定具有良好重访特性的最优解。
太阳同步回归轨道;重访特性;基本交点距;贝祖定理
遥感卫星等对地观测卫星近年来取得了长足发展,对地观测的空间分辨率可达米级,甚至亚米级,在军事、民用等领域均有重要应用。由于遥感卫星所搭载的光学成像载荷(如星载CCD传感器)要求光照条件相对稳定,且根据任务需求,遥感卫星应在一定时间内对特定区域进行重复观测。因此,太阳同步回归轨道广泛地被对地观测卫星所采用。
太阳同步回归轨道具有太阳同步和回归轨道的双重特点,满足遥感卫星的任务要求。早期的轨道设计主要以经验为主,没有通用的准则,限制了遥感卫星轨道设计的规范化发展[1]。近年来,随着对卫星轨道理论的深入探索,众多学者针对太阳同步回归轨道的设计优化及重访特性开展了相关研究。
Casey等[2]将一太阳日内卫星绕地球的旋转周数定义为Q值,并利用Q值研究了太阳同步回归轨道卫星在回归周期内的访问顺序。针对回归轨道的重访特性,袁孝康[3]给出了近似确定回归轨道重访周期的方法,以此筛选最优的回归轨道。然而,在一些特定情况下,这种方法会遗漏最优解。曲宏松等[4]将Q值作为联系太阳同步轨道和回归轨道的桥梁,基于Q值和袁孝康[3]给出的方法探究了在一定高度范围内的太阳同步轨道,并给出相对最优解。郭晨光[5]将Q值的选取与卫星光学载荷的时间分辨、空间分辨率等约束条件相结合,给出优化轨道回归和重访特性的方法。谢金华[1]针对重访周期,进行了较深入的研究,给出卫星对地面目标重访的基本条件及星载光学载荷覆盖范围的确定方法。针对中国航天HJ-1A/1B双星的实际任务,谭田等[6]以星载CCD相机的幅宽为基础,设计了重访周期为2天的双星星座。此外,Pie等[7]引入回归轨道子循环的定义,并借助回归周期内卫星星下点轨迹相对于回归周期开始时的偏差,将长回归周期轨道进行了合理划分,以减少重访时间。Nadoushan等[8]基于数论来设计太阳同步回归轨道,使其具有特定的重访周期和最优的侧摆角。
本研究在总结太阳同步回归轨道形成条件的基础上,探究轨道在回归周期内的访问顺序,以及轨道的重访特性。此外,以光学载荷对地观测为前提,列举了特定回归周期轨道的地面覆盖特性。最后,以一轨道高度范围为约束条件,分析给出了满足覆盖要求与重访特性的太阳同步回归轨道。
1 太阳同步回归轨道
太阳同步回归轨道具有太阳同步轨道和回归轨道的双重性质,既能保证特定的光照条件,又能实现对特定区域的周期性观测,因此被诸多对地观测卫星所采用。本章分别给出太阳同步轨道和回归轨道的形成条件,并将两者结合,给出太阳同步回归轨道的Q值。
1.1 太阳同步轨道
卫星轨道平面的取向由升交点赤经Ω和轨道倾角i共同决定。由摄动理论可知,轨道倾角平均无变化,而Ω的平均变化率WΩ为[9]
(1)
式中: J2为地球非球形摄动的一阶长期项; μ为地球引力系数;a为轨道半长轴;Re为地球赤道半径;e为轨道偏心率;i为轨道倾角。
可知,WΩ相当于轨道平面绕地球轴线的进动角速度,若其值等于地球的公转角速度,则轨道平面相对于太阳具有固定的取向,进而得到太阳同步轨道。由文献[10]可知,太阳同步轨道的条件为
(2)
式中isso太阳同步轨道的倾角。
1.2 回归轨道
回归轨道是指经过特定轨道日后,星下点轨迹重复出现的轨道。由文献[9],轨道日PEO为
(3)
式中:ωE为地球自转角速度。由文献[9]可知,卫星的交点周期Pnod为
(4)
式中:Wω是近地点幅角的平均变化率; WM是平近点角的平均变化率,其值分别为
若在整数个轨道日内,卫星绕地球旋转整数圈,则满足星下点轨迹重复出现的条件,回归轨道条件可表示为
(5)
式中D,N为互质的整数。
在轨道为太阳同步轨道的前提下,轨道日与太阳日相等,即PEO=86 400s。定义太阳同步回归轨道的Q值为
(6)
Q值表示一交点日内,卫星的旋转周数。为便于研究,将Q值表示成
(7)
式中:ν为将Q向下取整得到的数,d=N-νD。
2 回归轨道的访问特性
回归轨道的Q值决定轨道星下点轨迹的位置和访问顺序。本章给出Q值与回归轨道访问顺序的关系,并以数论中的贝祖定理为基础,分析回归轨道的重访特性。
2.1 访问顺序
由1.2可知,D天回归的轨道,绕地球N周。N个交点(升交点或降交点)将地球的赤道周长分成了均等的N份,将相邻降交点间的距离定义为“格点距离”δg[11],格点距离是空间上相邻两个交点间的距离,可知
(8)
且卫星每天绕地球Q周,连续两个交点间的距离被定义为“基本交点距”δb[11],基本交点距是时间上相邻两个交点间的距离,则
(9)
由式(6),可知
(10)
即一个基本交点距可被均分为D个格点距离。赤道上N个交点可用来描述回归周期内,轨道的访问情况。但若回归周期较长,N值较大,这种方法则不便于描述轨道的访问情况。考虑到回归轨道的性质,可取基本交点距内的交点来描述访问情况。
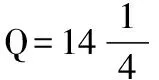
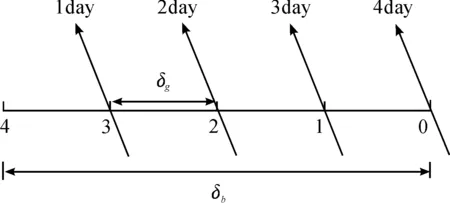
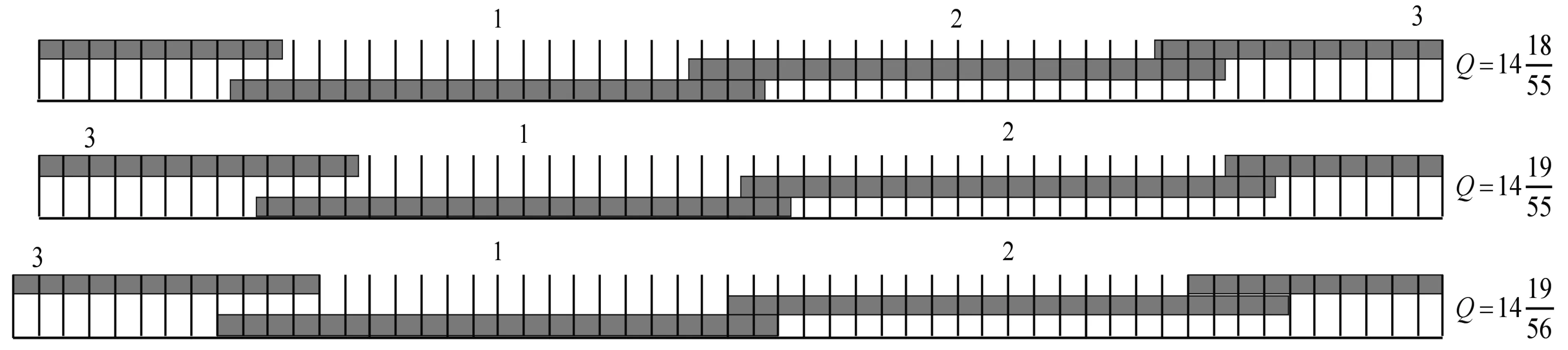
图1 4天回归轨道的访问特性
可以看出,轨道的回归周期为4天,且第2天的地面轨迹将从第1天的地面轨迹向东移动一个格点距离。通过对Q值进行分析可以得到,D决定了基本交点距内的格点距离数,而d决定了回归周期内,地面轨迹的访问顺序。如图2所示,给出某Q值的回归轨道在第k天的地面访问情况。
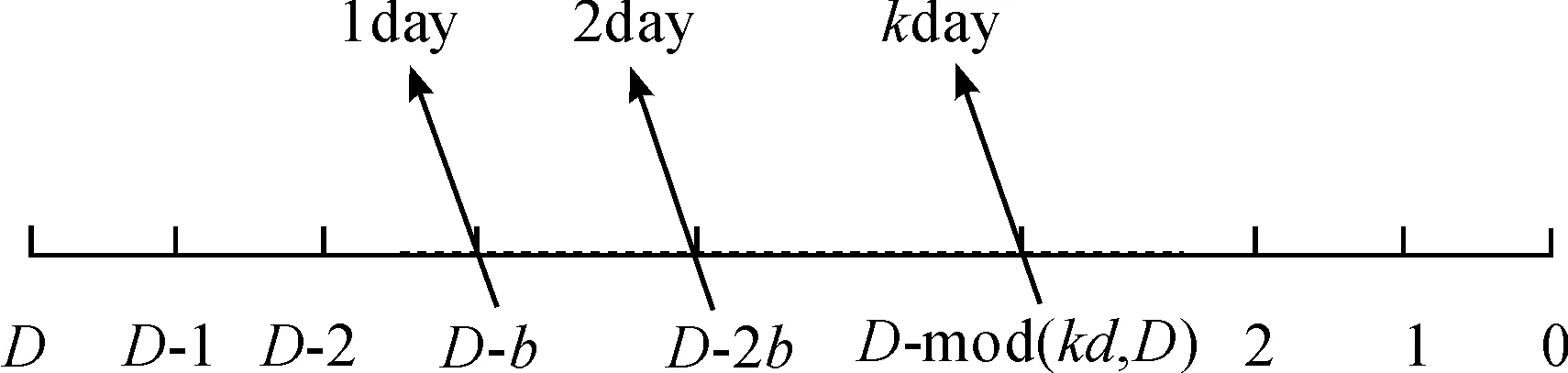
图2 D天回归轨道的访问特性
可归纳出某Q值对应的回归轨道,第k天的交点在基本交点距内的位置为
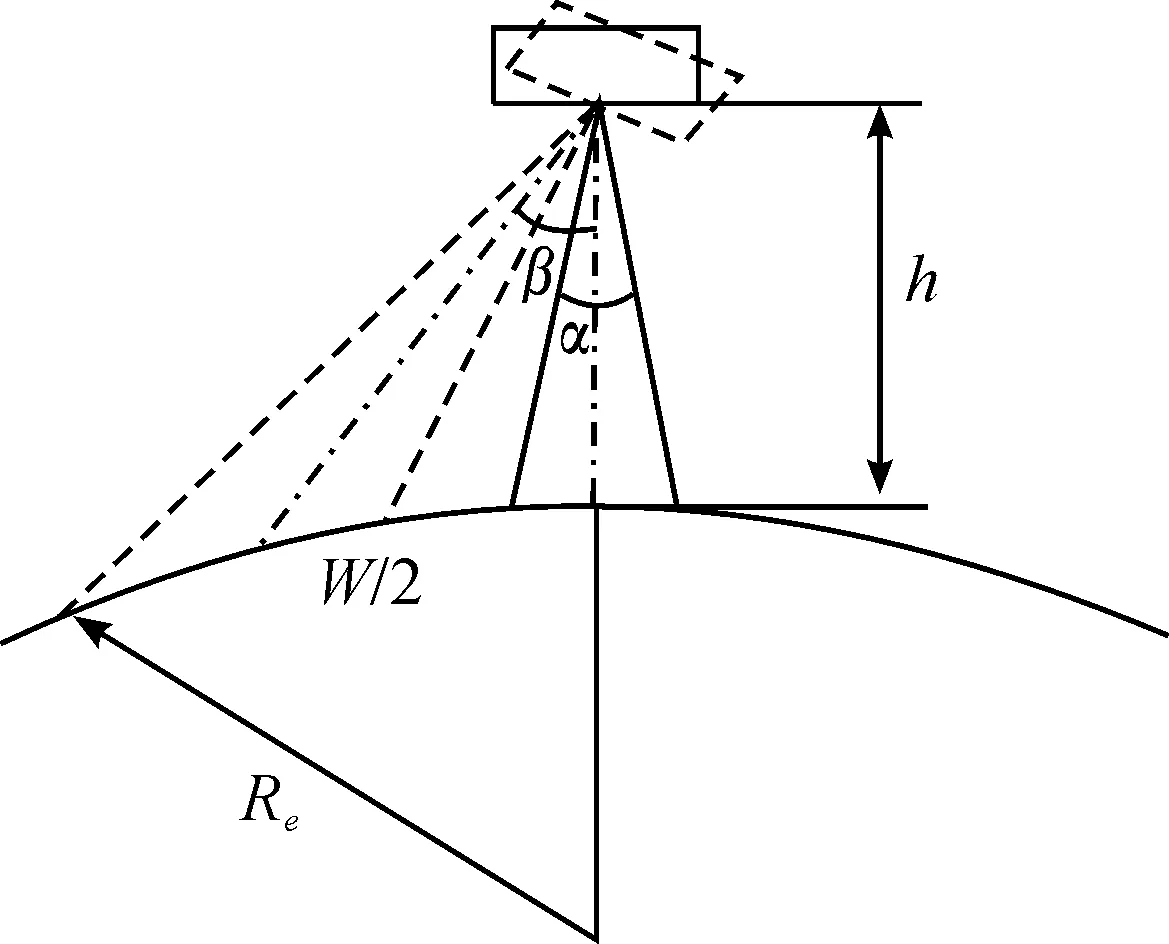
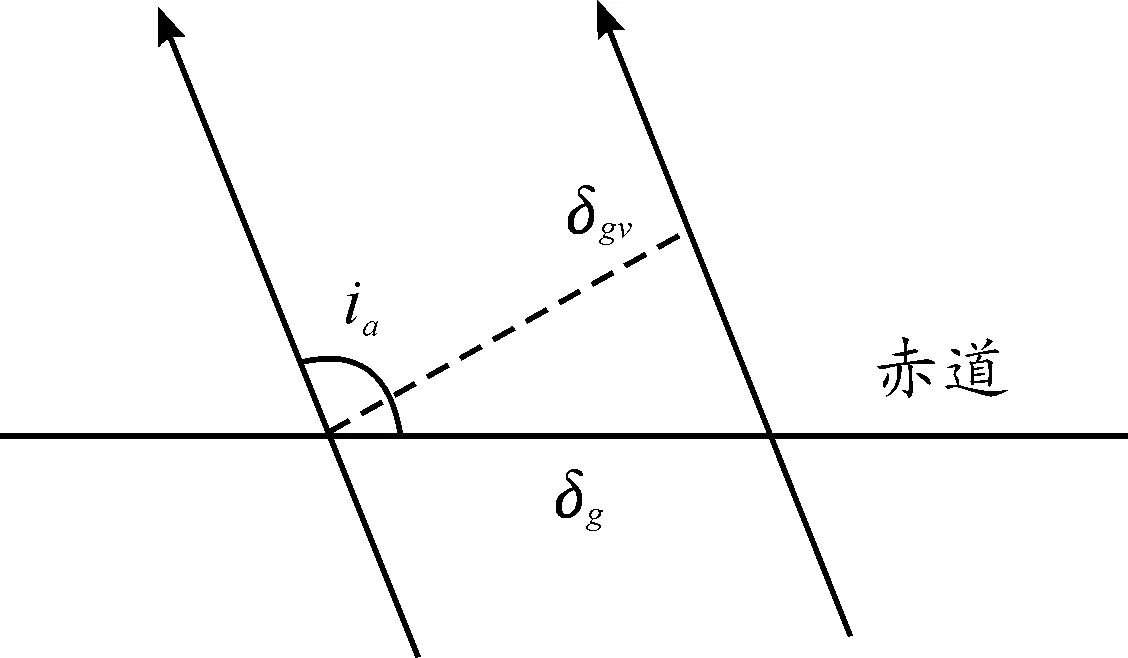
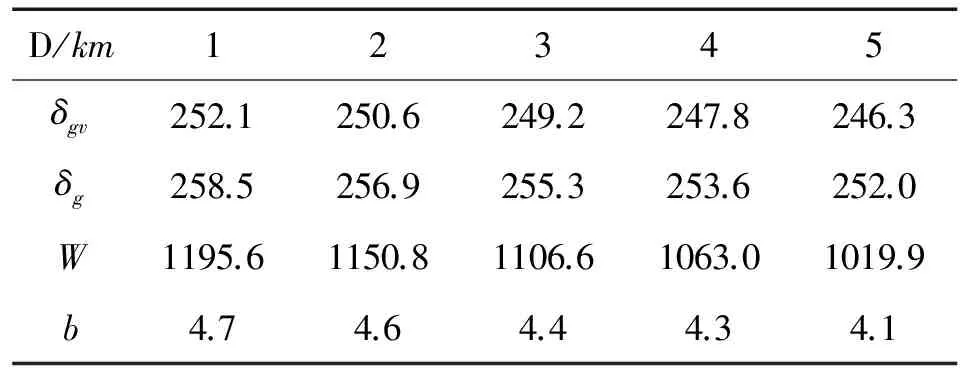
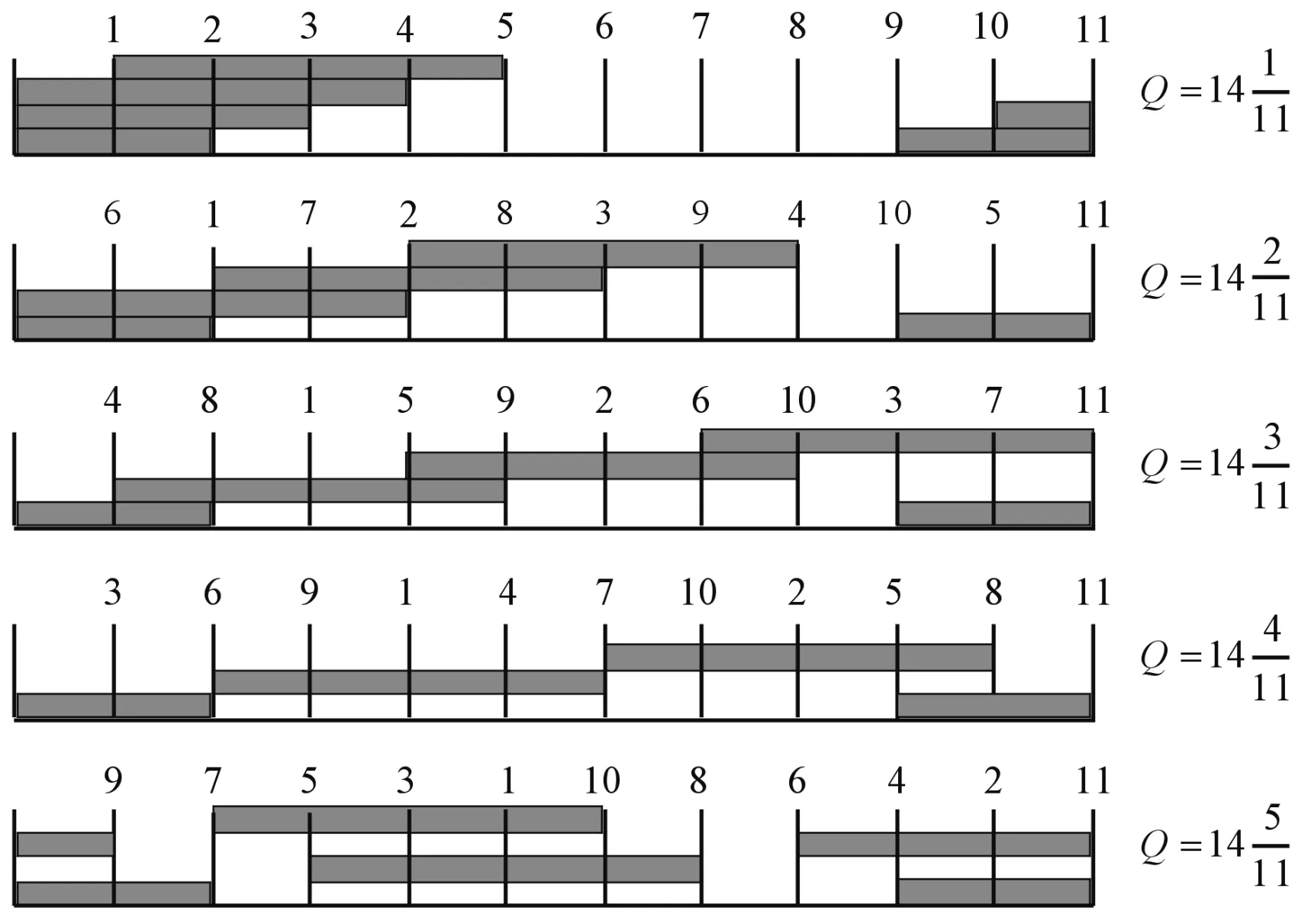
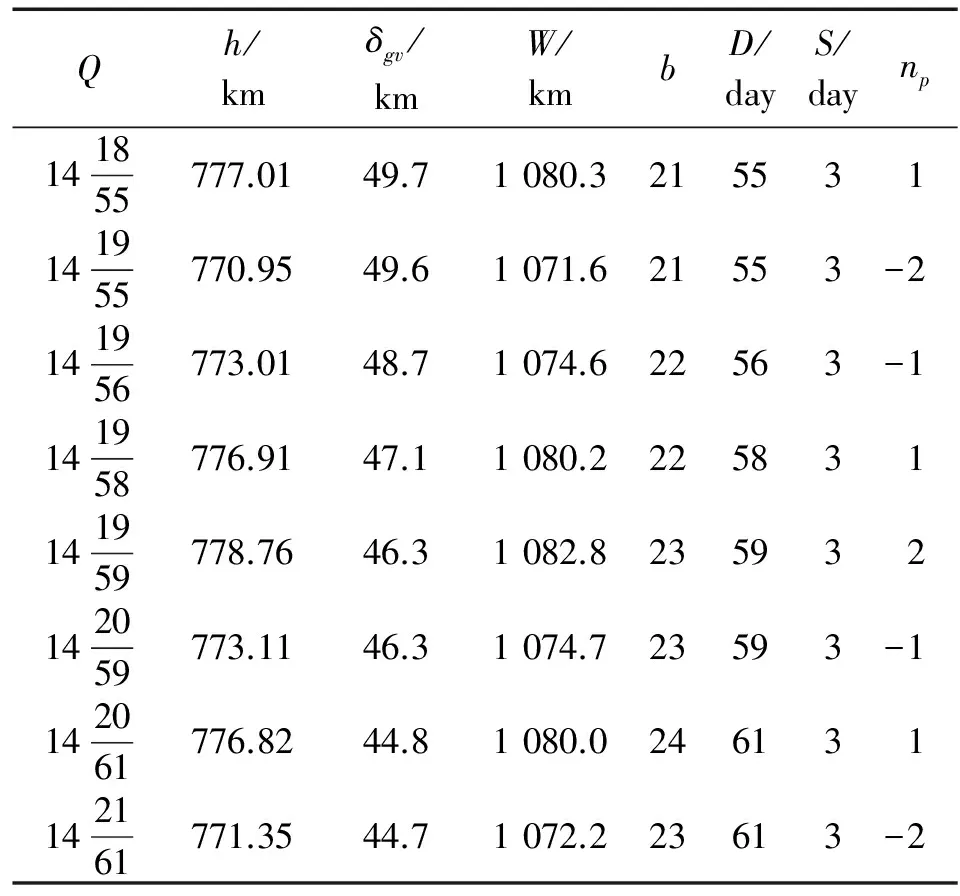
y=D-mod(kd,D) 0 (11) 式中,mod为取余函数。 分析知:① d=1或d=D-1,则第2天的地面轨迹将从第1天的地面轨迹向东或西移动一个格点距离,此类型的轨道可进行逐天连续覆盖,但难以实现对某些区域的快速重访;② d≠1且d≠D-1时,地面轨迹将从前一天的基础上移动数个格点距离,特定情况下,此类轨道可满足快速重访的要求;③ d=x与d=D-x的地面轨迹在空间上相互对称,因而在进行访问特性的快速分析时,可以仅分析d<0.5D所对应的轨道。图3给出回归周期为7天的各个轨道访问顺序。 2.2 重访特性 对于回归周期较长的卫星,通常要求其具有比较快速的重访能力,即具有较短的重访周期。重访周期是卫星有效载荷连续两次访问某地面目标的时间间隔,其值受到轨道高度,有效载荷的视场角,卫星侧摆能力等因素的影响,通常情况下不为定值。 以往研究通常以一个分母较小的分数来近似Q值的分数部分,且取这个较小的分母作为轨道的重访周期。显然,这种方法缺少一定的合理性。 图3 7天回归轨道的访问特性 假设近似的重访周期为S,根据卫星对地观测载荷的限制,希望S天后的地面轨迹与S天前的地面轨迹尽量较小,进而实现重访。根据文献[1],近似重访周期S满足 (12) 式中:m为正整数;np为非零整数;[*]为取整运算。 实际上,np为重访周期前后两条星下点轨迹相差的格点距离数,正值表示东向偏差,负值表示西向偏差。考虑到卫星对地观测范围的限制,为保证实现重访,np应尽量小。文献[3-4]中将np严格限定为±1,具有一定的实际意义,但是在某些特定情况下可能会遗漏最优解。 变换式(12)形式,整理得到 (13) 式(13)表示的是以d、D为系数,S、m为参数的丢番图方程,与文献[8]中给出的公式相似,但是更有实际意义。式(13)中,d与D互质,可以被非零整数np整除。由贝祖定理[12]可知,对于任意非零整数np,式(13)必存在整数解S和m,其中S表示回归轨道的近似重访周期。 至此,在给定回归轨道Q值的基础上,可通过求解丢番图方程,定量确定满足特定要求的近似重访周期。实际中,重访周期的确定还应考察卫星实际的覆盖特性,进而确定重访周期是否合理。 卫星的可观测范围W受卫星轨道高度h,载荷视场角α及最大侧摆角β的影响。对W进行量化计算,取卫星处于赤道上空的可观测范围进行分析,如图4所示。 可得W的计算公式为 (14) 式中:γ为卫星可观测角,且γ=β+0.5α。 相应地,取回归轨道在空间上连续两轨间距δg进行分析,如图5所示。 图4 卫星的可观测范围 图5 相邻轨迹的间距 图5中,ia为赤道与星下点轨迹的夹角,对于偏心率较小的回归轨道,其值为[11] (15) δgv为相邻两轨道的垂直距离,且其值为 (16) 可知,回归轨道卫星可以实现全球覆盖的条件为 (17) 式中,b为卫星可观测的轨迹间隔数。 仿真算例选取ZY-1(02)C[5]卫星的参数进行重访特性的研究。ZY-1(02)C星的视场角为4°,最大侧摆角为32°。取回归周期为11天的太阳同步回归轨道,则D=11,设定ν=14,且由2.1给出的回归轨道访问顺序的对称性,取d<0.5D的一系列轨道进行分析。得到覆盖特性如表1所示。 表1 太阳同步回归轨道的覆盖特性 根据表1的数据,通常要求对地观测卫星的重访周期在4天左右,图6给出了各轨道在回归周期内的访问顺序与4天内覆盖特性。 图6 访问顺序与覆盖特性 分析表1和图6可知,在考虑卫星可观测范围的情况下,若b=d,则轨道具有较好的重访特性。可充分利用卫星的载荷,实现对地面目标的快速重访。 结合前几章的相关内容,本章以实例给出满足一定约束条件的太阳同步回归轨道的设计方法。取卫星对地观测载荷的视场角为4°,卫星最大侧摆角为32°,要求对地观测影像的旁向重叠率q≥5%,则在770≤h≤780 km的高度范围内确定最优的太阳同步回归轨道。 取圆轨道进行分析,可由轨道高度范围确定半长轴a的取值范围,由式(2)可确定太阳同步轨道倾角的取值,结合式(4)(6),可得轨道Q值的取值范围为:14.318 3≤Q≤14.348 3,则ν=14,0.318 3≤d/D≤0.348 3。 卫星对地观测时,为了保证观测品质。通常在不考虑侧摆的情况下,要求相邻两轨道的观测幅宽有一定的重叠率。但重叠率过大则浪费星上资源。在此设定5%≤q≤15%。由式(14)可确定卫星的观测幅宽为:537.82≤W≤544.80 km,考虑到重叠率的限制,得到卫星的有效观测幅宽为457.14≤We≤517.56 km。 要求满足全球覆盖,则 NWe≥2πRe (18) 可得775≤N≤876,结合式(7)及Q的取值范围,可得:54≤D≤61,即轨道的回归周期从54到61天变化。表2给出在770~780 km高度范围内,所有满足要求的备选轨道,并给出相应的参数。 表2 备选轨道及其参数 针对太阳同步回归轨道的重访问题,提出了确定重访特性的系统方法。该方法将回归周期内的访问顺序加以量化,并以贝祖定理为依据,将重访周期的确定转化为丢番图方程的求解。考虑到重访周期受轨道高度、有效载荷的视场角,卫星侧摆能力等因素的影响,仿真算例以光学载荷对地观测为前提,给出特定回归周期轨道的重访特性;并将轨道高度范围作为约束,确定了具有优良重访特性的太阳同步回归轨道。 图7 备选轨道的覆盖特性 [1] 谢金华.遥感卫星轨道设计[D].郑州:中国人民解放军信息工程大学,2005. [2] CASEY D,WAY J.Orbit selection for the EOS mission and its synergism implications[J].IEEE Transactions on Geoscience and Remote Sensing,1991,29(6):822-835. [3] 袁孝康.星载合成孔径雷达导论[M].北京:国防工业出版社,2003. [4] 曲宏松,张叶,金光.基于Q值选取的太阳同步回归轨道设计算法[J].光学精密工程,2008,16(9):1688-1694. [5] 郭晨光.陆地观测卫星轨道优化与运控策略的研究[D].廊坊:北华航天工业学院,2014. [6] 谭田,杨芳.环境减灾-1A/1B卫星星座轨道设计[J].航天器工程,2009,18(6):27-30. [7] PIE N,SCHUTZ B E.Subcycle analysis for ICESat’s repeat groundtrack orbits and application to phasing maneuvers[J].The Journal of the Astronautical Sciences,2008,56(3):325-340. [8] NADOUSHAN M J,Assadian N.Repeat ground track orbit design with desired revisit time and optimal tilt[C].Aerospace Science and Technology,2015,40:200-208. [9] 肖业伦,韩潮.航天器动力学[M].北京:北京航空航天大学出版社,2006. [10]肖业伦.航天器飞行动力学原理[M].北京:中国宇航出版社,1995. [11]CAPDEROU M.Satellites:orbits and mission[M].Berlin:Springer,2005. [12]ROSEN K H.Elementary number theory and its applications[M].6th edition.Beijing:China Machine Press,2010. (责任编辑 杨继森) Research on Revisit Properties for Sun-Synchronous RGT Orbits’ Satellite JIA Xiang-hua, XU Ming (School of Astronautics, Beihang University, Beijing 100191, China) The system approach is put forward to explore the revisit properties for the sun-synchronous RGT orbit. This approach bases on theQvalue to combine sun-synchronous orbit and RGT orbit, and quantifies the problem of visit order during one repeat cycle with the use of base interval. Besides, by employing the Bezout’s theorem of number theory, the problem of determining the revisit cycle is transformed into solving a diophantine equation. The earth observation through optical payloads is chosen as the precondition for simulation examples, and then the visit order for some specific repeat cycle and the coverage condition of satellite are acquired. Finally, corresponding revisit properties are achieved. Besides, the design method of sun-synchronous RGT orbit is given to realize fast revisit with the constraint of orbital altitude range. Numerical simulations have shown that this method can determine the optimal orbit equipped with good revisit properties. sun-synchronous RGT orbit; revisit property; base interval; Bezout’s theorem 2016-12-25; 2017-01-22 基金项目:国家自然科学基金项目(11172020);北京市自然科学基金项目(4153060) 贾向华(1991—),男,硕士研究生,主要从事航天器轨道动力学研究。 徐明(1981—),男,副教授,博士生导师,主要从事航天器轨道动力学与控制等研究。 10.11809/scbgxb2017.05.037 format:JIA Xiang-hua, XU Ming.Research on Revisit Properties for Sun-Synchronous RGT Orbits’ Satellite[J].Journal of Ordnance Equipment Engineering,2017(5):159-163. V19 A 2096-2304(2017)05-0159-05 本文引用格式:贾向华,徐明.太阳同步回归轨道卫星的重访特性研究[J].兵器装备工程学报,2017(5):159-163.
3 覆盖特性分析
4 轨道设计
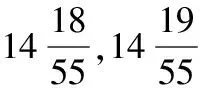
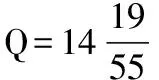
5 结论