关于Banach代数中伪Drazin逆的进一步结果

邹红林 陈建龙

(东南大学数学学院, 南京 210096)

关于Banach代数中伪Drazin逆的进一步结果

邹红林 陈建龙

(东南大学数学学院, 南京 210096)

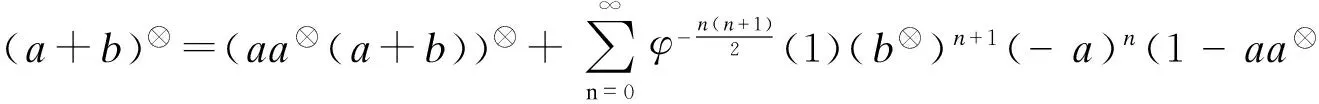
伪Drazin逆；Jacobson根；Banach代数

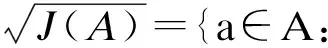
2012年,Wang等[1]在环和Banach代数中引入了伪Drazin逆的概念,并且在一定条件下给出了2个伪Drazin可逆元之和的伪Drazin逆的表达式. 2014年,Zhu等[2]讨论了Banach代数中2个伪Drazin可逆元a,b在满足ab=λba(λ≠0)时,a+b的伪Drazin逆存在的充要条件和表达式；同时, 在此条件下给出了ab的伪Drazin逆的表达式. 本文在条件ab=φ(ba)下，研究了ab与a+b的伪Drazin逆的表达式,其中φ为A上双射的centralizer,a,b为伪Drazin可逆元.

1 定义和引理

1.1 定义

定义1[3]设φ:A→A是一个映射. 若对任意的a,b∈A, 有φ(ab)=aφ(b)=φ(a)b, 则称φ是A上的centralizer.

显然, 对于任意的非零复数λ, 映射:a→λa(a∈A)是A上双射的centralizer.

定义2[1]设a∈A. 若存在x∈A, 满足

则称a是伪Drazin可逆的. 满足上述条件的元素x, 称为a的伪Drazin逆. 若a的伪Drazin逆存在, 则必是唯一的, 记为a⊗. 用ApD表示A中的所有的伪Drazin可逆的元素组成的集合. 若a∈ApD, 记aπ=1-aa⊗.

设p∈A是幂等元, 则元素a∈A可写成如下矩阵表达式:

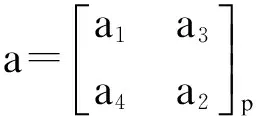
不难看出, 把a∈A表示成上面的矩阵形式, 若φ是A上的centralizer, 则有

根据文献[4], 对任意的a∈ApD, 取p=aa⊗, 则a和a⊗可表示为

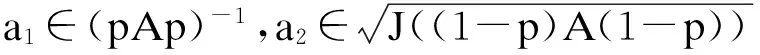
1.2 引理

引理1[3]设φ:A→A是centralizer, 则对任意的正整数n, 下列陈述成立:

1) φn是A上的centralizer;

2) 对任意的a∈A, 有(φ(a))n=φn(an);

3) 若φ是双射, 则φ-n是A上的centralizer.

引理2[3]设φ:A→A是centralizer. 若a,b∈A满足ab=φ(ba), 则对任意的正整数n, 下列等式成立:

1) abn=φn(bna);

2) anb=φn(ban);

3) anbn=φn2(bnan);

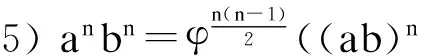
引理3[3]设φ:A→A是centralizer, 则

1) 对任意a∈A, 有φ(1)a=aφ(1);

2) 对任意的a,b∈A, 有φ(a+b)=φ(a)+φ(b).

引理4[5]设a,b∈A, 则

1) 若a∈J(A)或b∈J(A), 则ab, ba∈J(A);

2) 若a∈J(A)且b∈J(A), 则a+b∈J(A).

引理5[1]设a,b∈ApD满足ab=ba, 则ab∈ApD且(ab)⊗=a⊗b⊗.

设A1和A2分别表示代数pAp和(1-p)A(1-p), 其中p2=p∈A.

引理7[4]设p2=p,x,y∈A且x,y具有如下矩阵表达式:

(1)

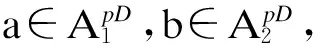
(2)

(3)

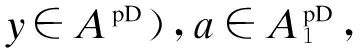
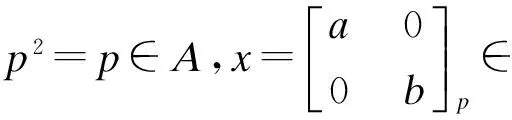
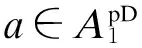
2 主要结论

首先给出以下几个命题.

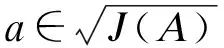
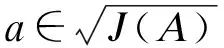
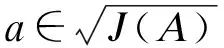
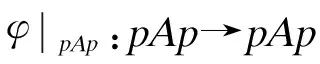
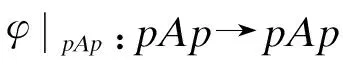
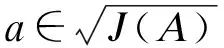
命题4 设φ:A→A是双射的centralizer. 若a,b∈ApD满足ab=φ(ba), 则

1) aa⊗b=baa⊗;

2) bb⊗a=abb⊗.

证明1) 记p=aa⊗, 则有

pb-pbp=pb(1-p)=pnb(1-p)= (aa⊗)nb(1-aa⊗)= (a⊗)nanb(1-aa⊗)= (a⊗)nφn(ban)(1-aa⊗)= (a⊗)nφn(1)ban(1-aa⊗)

这意味着

从而, 可得pb=pbp.另一方面

bp-pbp=(1-p)bp=(1-p)bpn= (1-aa⊗)b(aa⊗)n= (1-aa⊗)ban(a⊗)n= (1-aa⊗)φ-n(anb)(a⊗)n= (1-aa⊗)anφ-n(1)b(a⊗)n

这表明

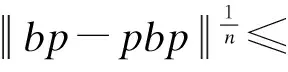
因此, 可得bp=pbp.

综上所述, 有aa⊗b=baa⊗.

证明2) 类似于证明1).

考虑ab=φ(ba)条件下，ab的伪Drazin逆的表达式, 推广了文献[2]中的相关结果.其中,φ是A上双射的centralizer，a,b是伪Drazin可逆元.

定理1 设φ:A→A是双射的centralizer. 若a,b∈ApD满足ab=φ(ba), 则

1) a⊗b=φ-1(ba⊗);

2) ab⊗=φ-1(b⊗a);

3) a⊗b⊗=φ(b⊗a⊗);

4) (ab)⊗=b⊗a⊗=φ-1(a⊗b⊗).

证明1) 根据命题4, 可知aa⊗b=baa⊗. 进而可得

a⊗b=a⊗aa⊗b=a⊗baa⊗=a⊗φ-1(ab)a⊗= φ-1(1)a⊗aba⊗=φ-1(1)ba⊗aa⊗= φ-1(ba⊗)

证明2) 相似于证明1).

证明3) 由证明1)和2)直接可证.

证明4) 考虑元素a和b相对于幂等元p=aa⊗的矩阵表达式:

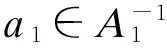
相似地, 可知b4=0. 因此,有

由已知条件ab=φ(ba), 可得

因此, a1b1=φ(b1a1),a2b2=φ(b2a2).

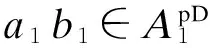
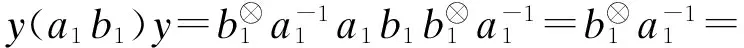
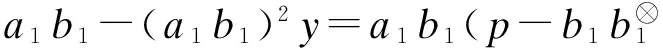
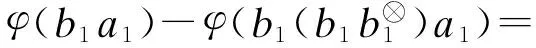
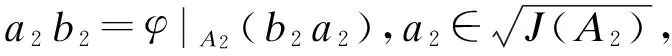
另外, 注意到

因此, 可得(ab)⊗=b⊗a⊗=φ-1(a⊗b⊗).

推论1[2]设a,b∈ApD满足ab=λba(λ≠0), 则

1) a⊗b=λ-1ba⊗;

2) ab⊗=λ-1b⊗a;

3) (ab)⊗=b⊗a⊗=λ-1a⊗b⊗.

在证明主要结果之前, 需要下面的辅助结论.

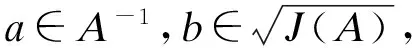
(a+b)-1= (1+a-1b)-1a-1=

下面的定理给出了Banach代数中2个伪Drazin可逆元之和的伪Drazin逆存在的充分必要条件以及表达式, 推广了文献[2]中的相关结论.

定理2 设φ:A→A是双射的centralizer. 若a,b∈ApD满足ab=φ(ba), 则下列条件等价:

1) a+b∈ApD;

2) u=aa⊗(a+b)∈ApD;

3) v=aa⊗(a+b)bb⊗∈ApD.

此时

(4)

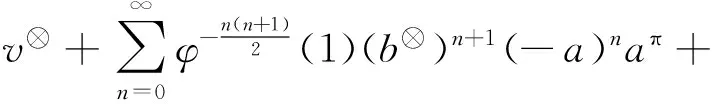
(5)

u⊗=aa⊗(a+b)⊗, v⊗=aa⊗(a+b)⊗bb⊗

(6)

证明 根据定理1的证明过程可知

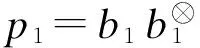
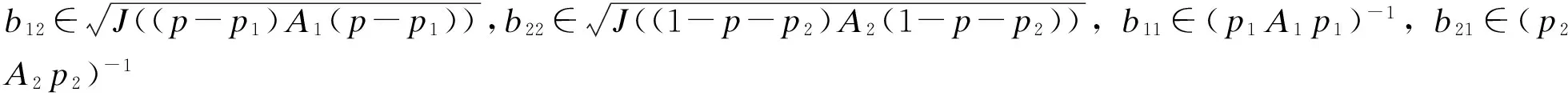
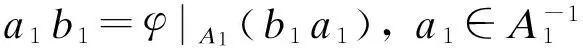
相似地, 可得

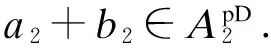
根据命题5, 可得a21+b21∈(p2A2p2)-1且

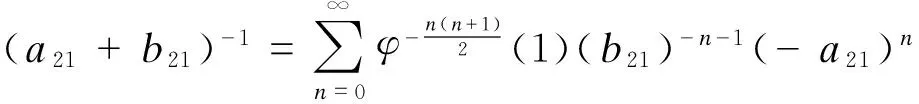
因为(b21)-1=b2⊗=b⊗aπ, 所以对任意的正整数n, 有(b21)-n-1=(b⊗)n+1aπ. 除此之外,可以验证

(baπ)(b⊗aπ)(aπa)=bb⊗aπa

这意味着对任意的正整数n, 有(-a21)n=bb⊗(-a)naπ. 因此

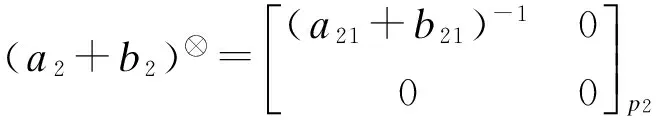
因为

1)⟺2) 由命题4, 可推出a1+b1=aa⊗(a+b)aa⊗=aa⊗(a+b)=u. 因此, a+b∈ApD当且仅当 u∈ApD. 另外, 易知式(4)成立.

1)⟺3) 根据命题5, 可得

a12+b12∈((p-p1)A1(p-p1))-1

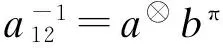
因为

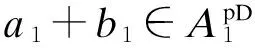
(a1+b1)⊗=(a11+b11)⊗+(a12+b12)-1

根据下面的矩阵表达式:

可知v=a11+b11. 因此, a+b∈ApD当且仅当v∈ApD. 最后, 通过计算可得式(5)和(6).

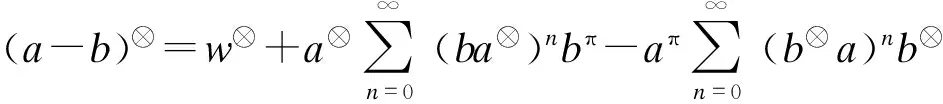
w⊗=aa⊗(a-b)⊗bb⊗

3 结语

本文主要研究了Banach代数中2个伪Drazin可逆元的积与和的伪Drazin逆的表达式, 推广了文献[2]中的相关结果. 因为伪Drazin逆是Drazin逆[6]的推广, 所以研究难度比Drazin逆更大. 目前关于伪Drazin逆的成果并不多[7], 还有许多问题值得思考.

)

[1]WangZ,ChenJL.PseudoDrazininversesinassociativeringsandBanachalgebras[J]. Linear Algebra and Its Applications, 2012, 437(6):1332-1345.DOI:10.1016/j.laa.2012.04.039.

[2]ZhuHH,ChenJL.AdditivepropertyofpseudoDrazininverseofelementsinBanachalgebras[J]. Filomat, 2014, 28(9):1773-1781.DOI:10.2298/fil1409773z.

[3]ZhuHH,ZhangXX,ChenJL.Centralizersandtheirapplicationstogeneralizedinverses[J]. Linear Algebra and Its Applications, 2014, 458:291-300.DOI:10.1016/j.laa.2014.06.015.

[4]ZouHL,ChenJL.OnthepseudoDrazininverseofthesumoftwoelementsinaBanachalgebra[J]. Filomat, 2017, 31(7):2011-2022.DOI:10.2298/fil1707011z.

[5]LamTY. A first course in noncommutative rings: Graduate texts in mathematics [M]. 2nded.NewYork,USA:Springer-Verlag, 2001:54-55.

[6]DrazinMP.Pseudo-inversesinassociativeringsandsemigroups[J]. The American Mathematical Monthly, 1958, 65(7): 506-514.DOI:10.2307/2308576.

[7]ZhuHH,ChenJL,PatricioP.RepresentationsforthepseudoDrazininverseofelementsinaBanachalgebra[J]. Taiwanese Journal of Mathematics, 2015, 19(2): 349-362.DOI:10.11650/tjm.19.2015.4576.

FurtherresultsonpseudoDrazininverseinBanachalgebras

ZouHonglinChenJianlong

(SchoolofMathematics,SoutheastUniversity,Nanjing210096,China)

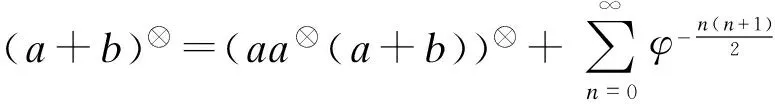
pseudoDrazininverse;Jacobsonradical;Banachalgebra

10.3969/j.issn.1001-0505.2017.03.034

2016-09-01. 作者简介: 邹红林(1982─), 男, 博士生; 陈建龙(联系人), 男, 博士, 教授, 博士生导师,jlchen@seu.edu.cn.

国家自然科学基金资助项目(11371089)、江苏省普通高校研究生科研创新计划资助项目 (KYZZ15-0049)、 江苏省自然科学基金资助项目(BK20141327).

邹红林,陈建龙.关于Banach代数中伪Drazin逆的进一步结果[J].东南大学学报(自然科学版),2017,47(3):626-630.

10.3969/j.issn.1001-0505.2017.03.034.

O

A

1001-0505(2017)03-0626-05