列车作用下桥梁应力响应计算方法比较

李慧乐 夏 禾 宗周红

(1东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096)(2北京交通大学土木建筑工程学院,北京 100044)

列车作用下桥梁应力响应计算方法比较

李慧乐1夏 禾2宗周红1

(1东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096)(2北京交通大学土木建筑工程学院,北京 100044)

为有效分析列车引起的桥梁应力响应,对车桥耦合动力分析法、静力影响线法及移动集中力法3种列车作用下的桥梁应力响应计算方法进行了深入的比较研究．采用3种方法对2座铁路典型混凝土简支T梁和下承式钢桁梁桥进行应力响应分析, 基于桥梁现场实测数据对比分析了不同方法的计算结果,研究了列车速度和桥梁横向振动对应力结果的影响．结果表明:车速对桥梁应力响应有显著的影响,共振发生时3种方法的计算结果相差较大,消振条件下三者区别减小;由列车水平方向作用力引起的桥梁或构件横向振动对应力响应的贡献不容忽视;车桥耦合动力分析法能够更为真实地反映桥梁构件的动应力历程,在高速、桥梁横向刚度较低或列车局部加载的情况下尤其具有计算精度优势．研究结果可为3种不同计算方法的工程应用提供参考．

应力分析;车桥耦合振动;现场测试;车速;横向振动

列车作用下桥梁的应力响应对于铁路桥梁的设计、评定(如疲劳评估)和维修加固等均具有重要作用,基于有限元法的数值计算是获取桥梁应力数据的有效途径．Nowack和Schulz[1]阐述了有限元法在结构疲劳应力分析中的重要价值,英国规范将其作为疲劳应力分析的一种严格方法进行推荐[2]．

在以往的研究中,常用的应力计算方法为静力影响线法和移动集中力法．静力影响线法是我国及欧美国家规范[3-6]采用的内力分析方法,为体现列车通过时对桥梁的冲击作用,通常在列车静轴重的基础上乘以一个动力放大系数[7]．近年来,研究人员倾向于采用动力分析方法来计算列车作用下桥梁构件的应力响应[8-9]．相应地,列车荷载被简化为一系列竖向平面内的移动集中力,各集中力的大小和间距与列车的实际轴重及排列相同．上述2种方法对车桥系统进行了较多的简化,所得应力结果可能与桥梁真实应力历程存在较大的差别．

近几十年来对于车桥耦合振动的研究较多,学者们建立了不同的分析模型[10-14],但以往的车桥耦合振动分析很少关注桥梁的应力响应．文献[15-16]采用较完善的车桥耦合系统模型计算了列车过桥引起的桥梁动应力,但未对车桥耦合动力分析法[15]与常用的静力影响线法及移动集中力法进行比较研究．

本文深入比较研究了上述3种列车作用下桥梁应力响应的计算方法,以阐述不同方法的计算精度及适用性,并为其工程应用提供参考和依据．选取铁路桥梁中具有代表性的混凝土简支T梁及下承式钢桁梁桥作为实例研究对象,利用现场实测数据对比分析3种方法所得应力计算结果,并探讨列车速度及桥梁横向振动对应力响应的影响．

1 3种应力计算方法

1.1 静力影响线法

影响线表征了构件某一截面随单位集中荷载加载位置不同的内力变化．运用线性叠加原理,列车荷载下桥梁构件应力可通过下式得到:

(1)

式中,S(t)为应力响应,随着列车在桥上位置的变化而变化;Pi为列车中第i(i=1,2,…,NT)个轮对的静轴重;ys()为所关心截面的应力影响线函数;Li(t)为第i个轮对在t时刻的位置;NT为列车总的轮对数．值得注意的是,静力影响线并不包含动力效应,式(1)中的t仅表示应力响应S(t)与列车在桥梁上的加载位置有关．

1.2 移动集中力法

移动集中力法将列车荷载简化为一系列竖向平面内的移动集中力,各集中力大小等于列车的静轴重,间距与轮对之间的实际距离相等．采用直接刚度法建立桥梁运动方程,可表示为

(2)

(3)

式中,Wi(t)为ND×1维分配向量,可将第i个轮对的轴重荷载分配到相应的桥梁节点上进行施加．

1.3 车桥耦合振动分析法[15]

车桥系统模型包括车辆子模型、桥梁子模型及轮轨相互作用模型．其中车辆模型由车体、转向架及轮对组成,转向架与轮对之间通过一系悬挂装置连接,车体与转向架之间通过二系悬挂装置连接,各悬挂装置简化为弹簧与阻尼．车体及转向架考虑横摆、点头、摇头、沉浮和侧滚5个自由度,轮对考虑横摆、摇头、沉浮和侧滚4个自由度(见图1)．

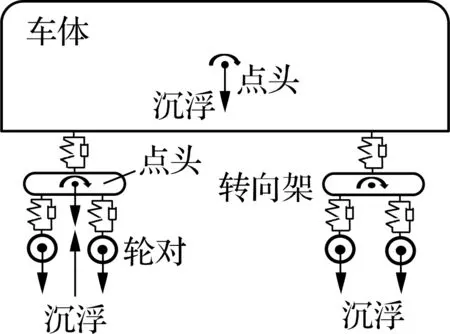
(a) 侧视图

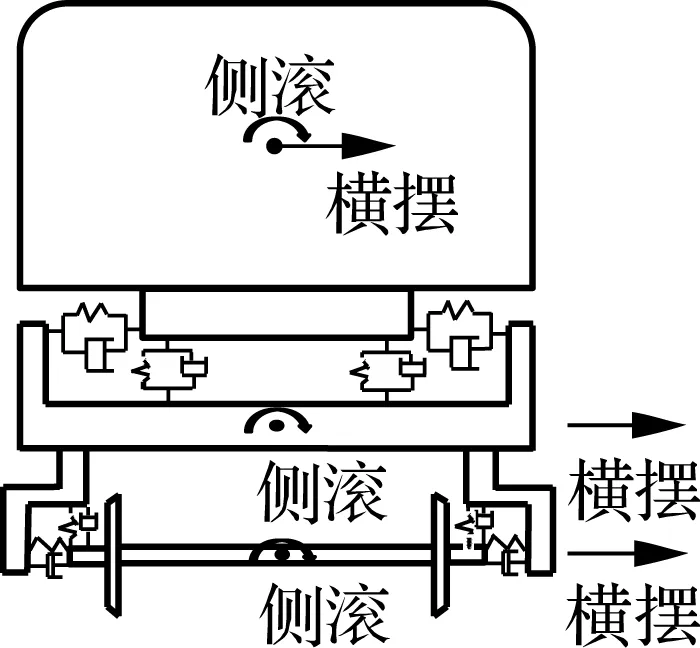
(b) 后视图

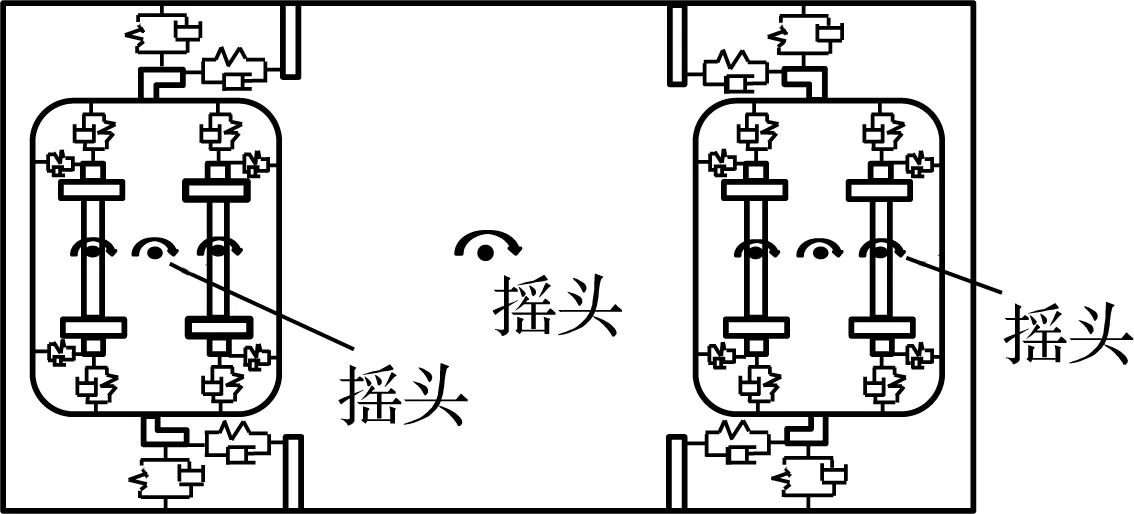
(c) 仰视图

假定各节车辆之间相互独立,则以单节车辆表示的列车运动方程为

(4)

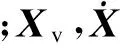
桥梁通过有限单元进行离散,并采用直接刚度法建立其运动方程,形式如式(2)所示．直接刚度法能够考虑桥梁所有振型的影响,适用于局部构件或结构细节的应力分析．列车施加在桥梁上的力向量Fb亦与轮轨相互作用模型有关．假定竖向轮轨为密贴状态,轮对竖向运动为轮位处桥梁运动与轨道不平顺的叠加,则轮对的沉浮与侧滚自由度并不完全独立．横向采用Kalker蠕滑理论,轮轨横向相互作用力取决于轮轨横向相对运动．根据上述轮轨关系所得到的桥梁运动方程、车辆运动方程右端的力向量Fb和Fv为桥梁、车辆运动以及轨道不平顺的函数,将力向量Fb和Fv中与桥梁、车辆运动有关的项移到方程左端,则车桥耦合系统的运动方程可写为

(5)

式中,Mvv=Mv;Mbb=Mb;Cvb,Cbv分别表示由车桥耦合效应产生的与桥梁、车辆相关的阻尼矩阵;Kvb,Kbv分别表示由车桥耦合效应产生的与桥梁、车辆相关的刚度矩阵;Pv和Pb分别为作用在车辆、桥梁上与轨道不平顺有关的力向量．

求解式(2)及(5),可计算得到移动力或车桥耦合系统模型下桥梁位移响应Xb(t)．根据有限单元理论,通过下式进一步求解单元动应变:

ε(t)=BXb(t)

(6)

式中,B为位移-应变转换矩阵,描述了单元内任一点应变与单元节点位移之间的转换关系,可由构件单元的形函数矩阵对空间几何坐标求导得到;ε(t)为动应变矩阵．

由弹性力学应力应变关系可得到动应力响应为

Sb(t)=DBXb(t)

(7)

式中,Sb(t)为桥梁单元动应力;D为单元弹性矩阵(应力-应变矩阵),对于给定的构件单元一般为常矩阵．

根据式(4)～(7)的理论,采用Matlab软件编制了计算程序．车桥系统动力方程(式(5))采用Newmark-β法进行数值积分求解,参数γ=0.5,β=0.25,积分时间步长为0.001 s．静力影响线法及移动集中力法则采用通用有限元软件ANSYS完成,ANSYS瞬态分析中求解式(2)所采用的时间步长为0.001 s．

2 混凝土桥实例分析

2.1 工程概况及动力测试

本文研究的混凝土简支梁桥位于朔黄铁路线,桥梁全长32.6 m,计算跨度为32 m．简支梁由2片T梁组成,通过混凝土横隔板连接在一起,其跨中截面如图2所示．

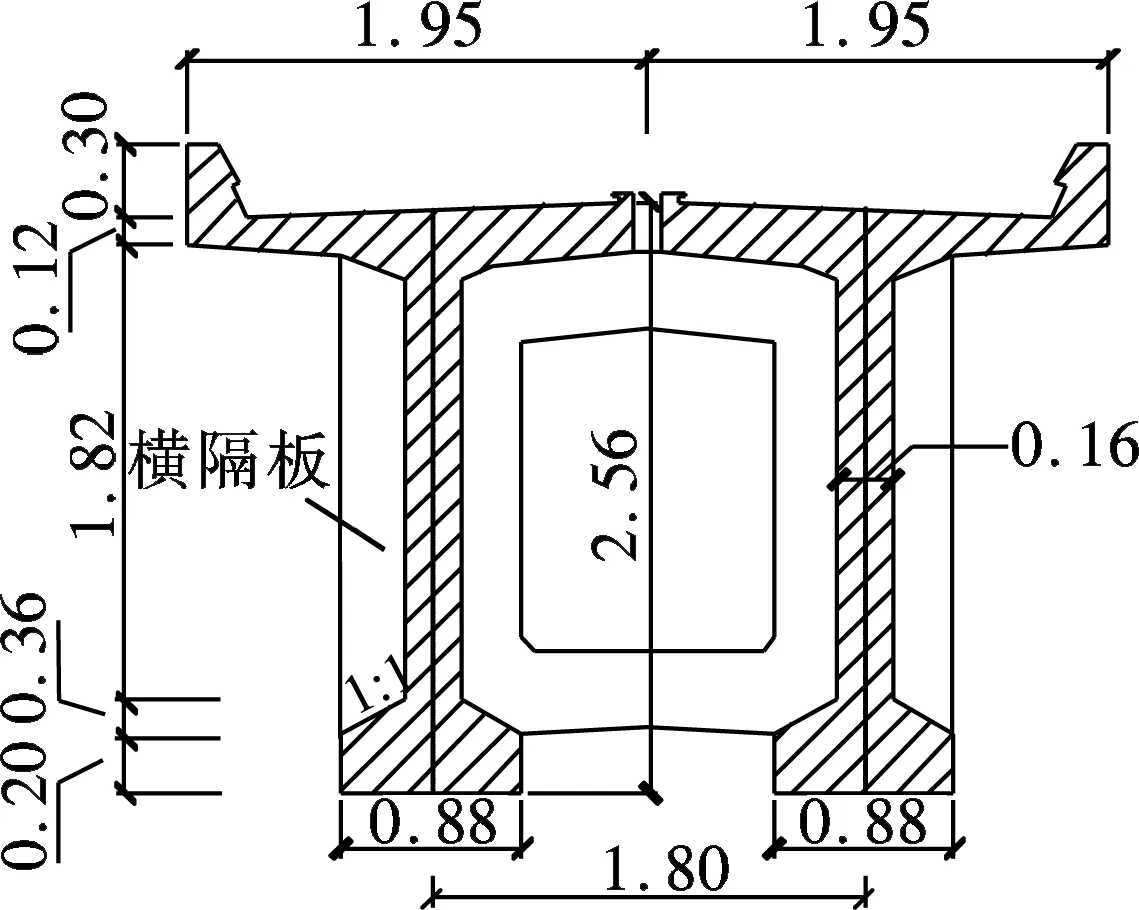
图2 桥梁跨中截面(单位:m)

受朔黄铁路发展有限公司委托,于2013年对该桥的运营性能进行了检定,期间对桥梁上、下部结构进行了动力测试．通过模态测试确定出梁体横向、竖向1阶自振频率,分别为2.9和5.5 Hz．此外,对桥梁在实际运营列车作用下的振动响应、动应变等进行了现场实测．

2.2 应力结果比较

为采用第1节中所述3种方法计算该桥在列车荷载作用下的应力响应,在ANSYS中建立了梁体有限元模型(见图3)．模型中2片T梁及横隔板均采用BEAM188单元模拟,并赋予各个单元实桥截面信息．横隔板单元在两端与T梁单元共用节点．

图3 32 m T梁有限元模型

受列车动载、腐蚀等效应的影响,该桥横向联系出现了一定程度的弱化．为充分利用实测数据并体现上述横向连接刚度弱化现象,同时考虑到横隔板厚的变化主要影响横向自振频率而对竖向频率几乎无影响,建模时对横隔板厚度进行了适当的调整．根据设计图纸,初始板厚取0.20 m,修正之后的厚度为0.13 m．

采用修正后的有限元模型计算得到桥梁横向、竖向1阶自振频率分别为2.98和5.43 Hz,与现场测试所得结果吻合．式(7)显示桥梁应力响应主要取决于位移响应,简支梁的位移由基阶振型控制．因此,采用所建立的有限元模型对该32 m简支梁桥进行应力响应计算是可行的．

选取现场实测的一个工况进行分析．过路列车编组为2台韶山SS4型机车牵引58辆满载的某型号敞车,列车全长729 m,行驶速度为70.6 km/h．在梁体跨中截面底部布置应变片,记录上述列车通过时的动应变时程．图4给出了实测与计算得到的动应变结果,数值计算采用基于车桥耦合动力分析的方法．轨道不平顺时域样本根据美国5级谱生成,由该等级轨道谱得到的轨道不平顺与我国干线铁路的不平顺较为接近．由图可知,现场实测与数值计算所得应变时程曲线的形状及幅值较为一致,说明所建立的车桥耦合系统模型能够较好地对列车引起的桥梁应变(应力)响应进行分析．

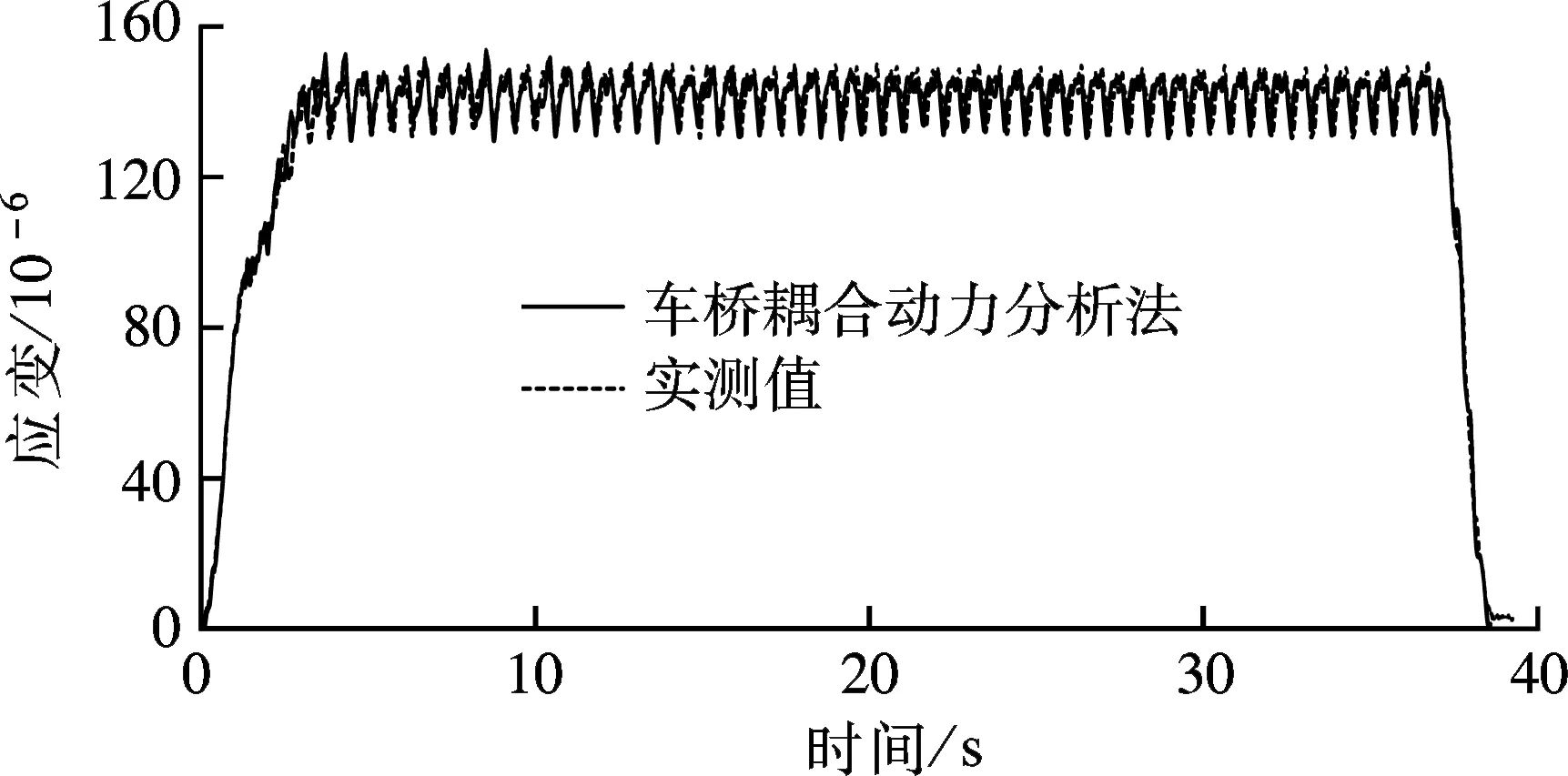
图4 实测和车桥耦合动力分析法的动应变时程曲线

图5比较了移动集中力法与车桥耦合动力分析方法所得的动应变响应时程．从图中可看出,二者存在差别．根据图4和图5的数据,计算得到移动集中力法、车桥耦合动力分析法结果与实测数据的平均残差分别为2.8×10-6和1.9×10-6,可见基于车桥耦合振动分析法的计算结果与实测数据更为接近．

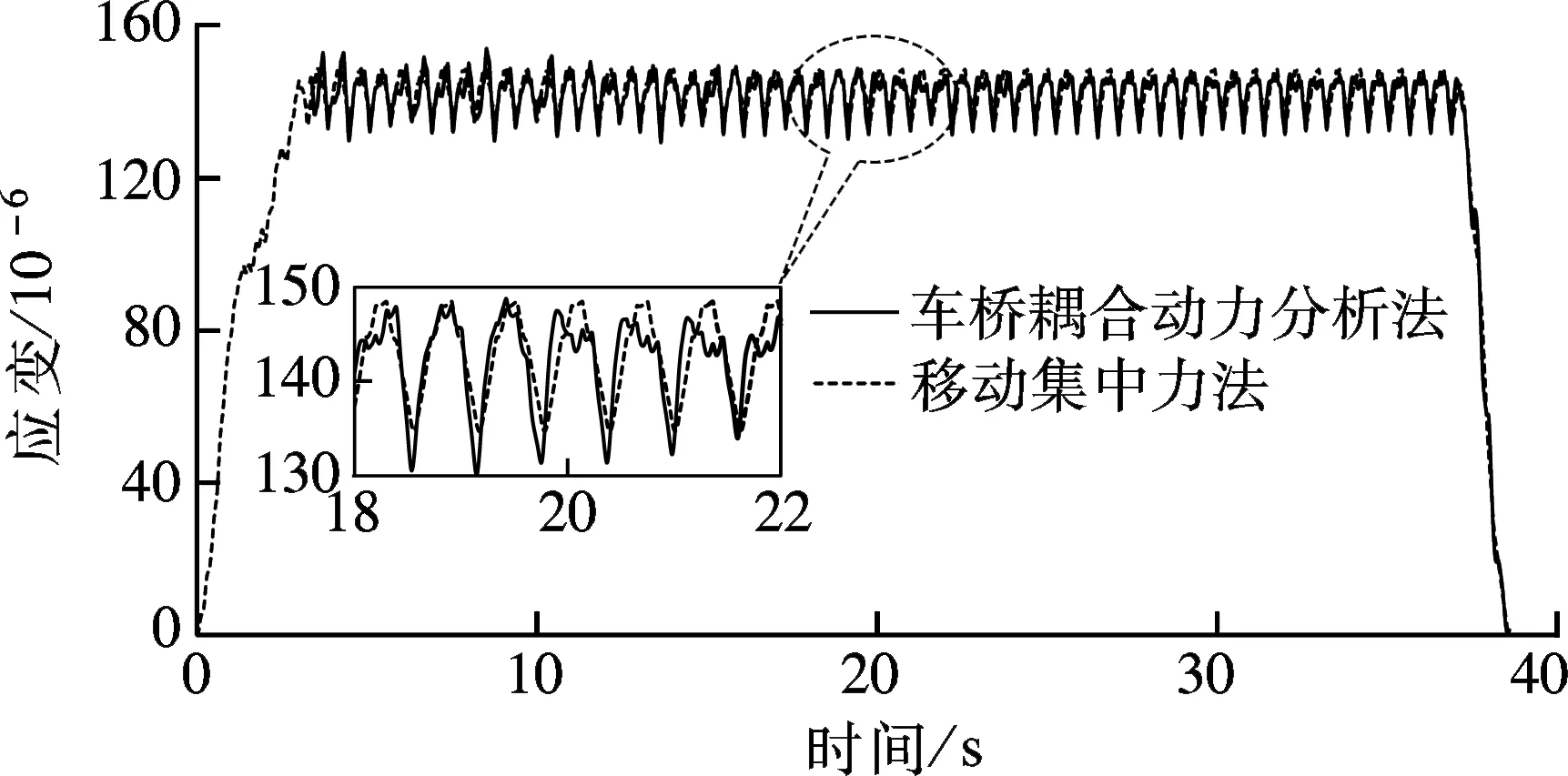
图5 移动集中力法和车桥耦合动力分析法的应变时程比较

2.3 列车速度影响

为研究车速对桥梁应力响应的影响,分别采用3种方法计算了上述简支梁桥在不同列车速度下的应力响应．2.2节已对所建立的货车-简支梁桥耦合振动模型进行了验证,因此本节仍采用该模型进行分析．选取计算车速范围为150～250 km/h,该范围虽已超出列车的实际车速,但此时车桥系统的动力效应较运营车速下更为明显,有利于考察3种方法真实反映车桥动力效应的能力．为减少计算耗时,列车编组缩短为2台机车牵引15辆满载敞车,荷载长213 m．

图6给出了移动集中力法和车桥耦合动力分析法得到的桥梁跨中截面应力放大系数随列车速度的变化情况．从图中可看出,这2种方法计算得到的应力放大系数均在某个车速出现峰值．文献[17]指出,在规则排列的列车轴重荷载作用下,简支梁将在某些车速出现共振和消振现象．共振发生时桥梁的响应较大,消振现象出现时响应则较小．移动轴重力下简支梁共振及消振车速计算公式分别为[17]

(8a)

(8b)

(8c)

式中,Vres,VcanI和VcanII分别为共振、第1类及第2类消振车速,km/h;L,Lv和Lch分别为桥梁跨度、车辆全长及车辆特征长度,m;f为桥梁竖向1阶自振频率,Hz;n为共振或消振的阶数．

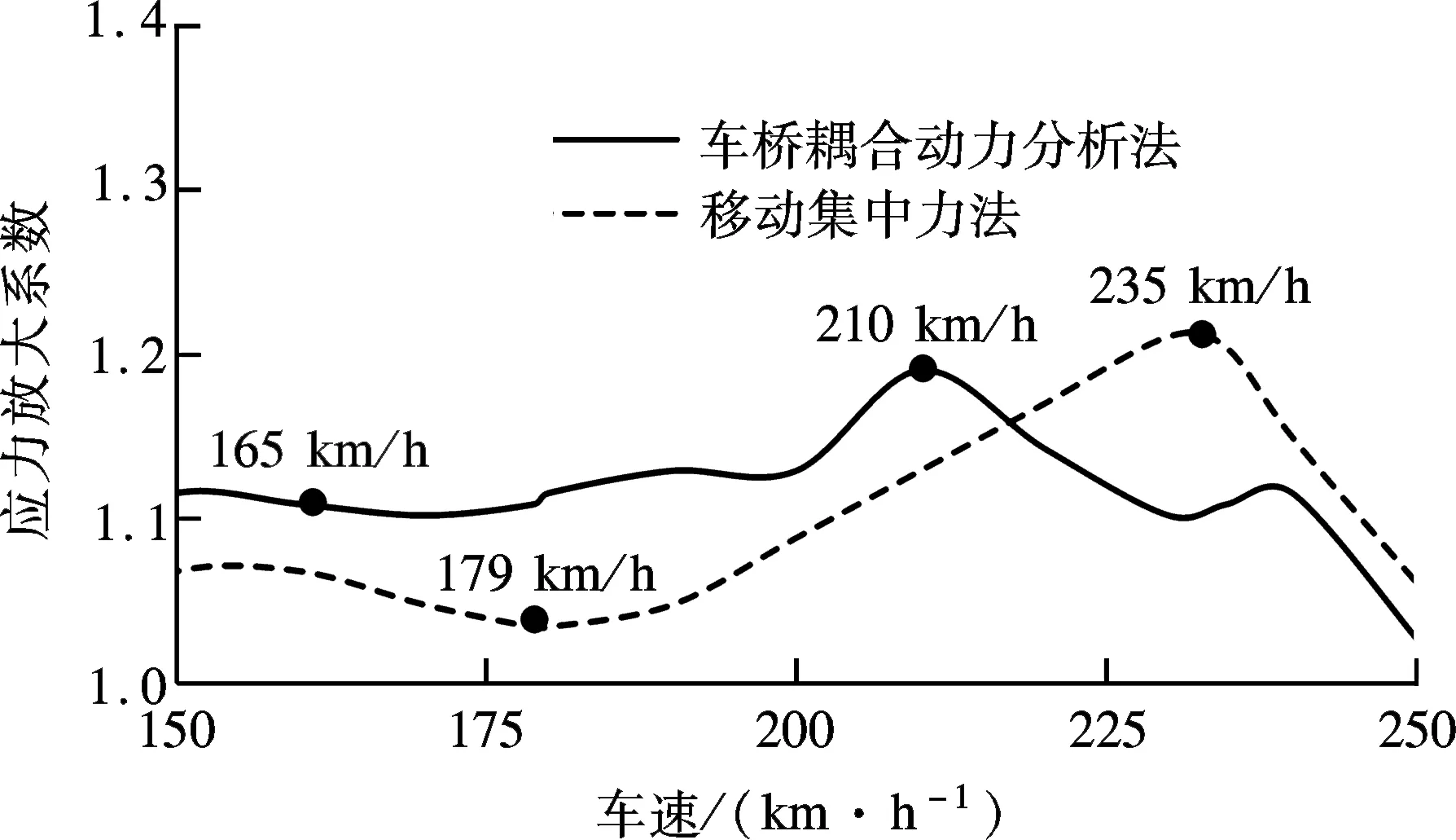
图6 不同计算方法得到的桥梁应力放大系数

过路列车编组中敞车的车辆全长、转向架中心距、轴距分别为12.00,8.20,1.83 m,简支梁竖向1阶自振频率为5.43 Hz,利用式(8)可计算得到所研究车速范围内的共振车速为235 km/h,消振车速为179 km/h．需要指出的是,式(8)是在假定列车荷载为一系列移动集中力时得出的．

从图6可看出,同一车速下2种方法所得应力放大系数有较大差别．移动集中力法所得应力放大系数在235km/h附近出现峰值,表明此车速下发生了共振效应,这与式(8)的预测一致．车桥耦合动力分析法所得应力放大系数的峰值则出现在210 km/h,这是因为耦合模型考虑了列车的质量,可视为桥梁的附加质量,从而降低了简支梁的自振频率,导致共振现象在较低速度下出现．类似情况亦出现在消振车速中:移动集中力作用时在179 km/h 下应力响应较小,发生消振现象;车桥耦合动力分析法中该消振速度则降至165 km/h左右．

图7给出了共振车速235及210 km/h下,采用3种方法计算得到的桥梁应变响应．显然,共振车速下应力响应的放大效应更为显著,此时静力影响线法的计算结果偏小,误差较大．移动集中力法与车桥耦合动力分析法的响应曲线亦不相同,因为二者所得出的共振车速存在区别．如前所述,移动集中力法无法考虑列车的质量效应,其共振现象发生在较高车速下．

(a) Vres=235 km/h

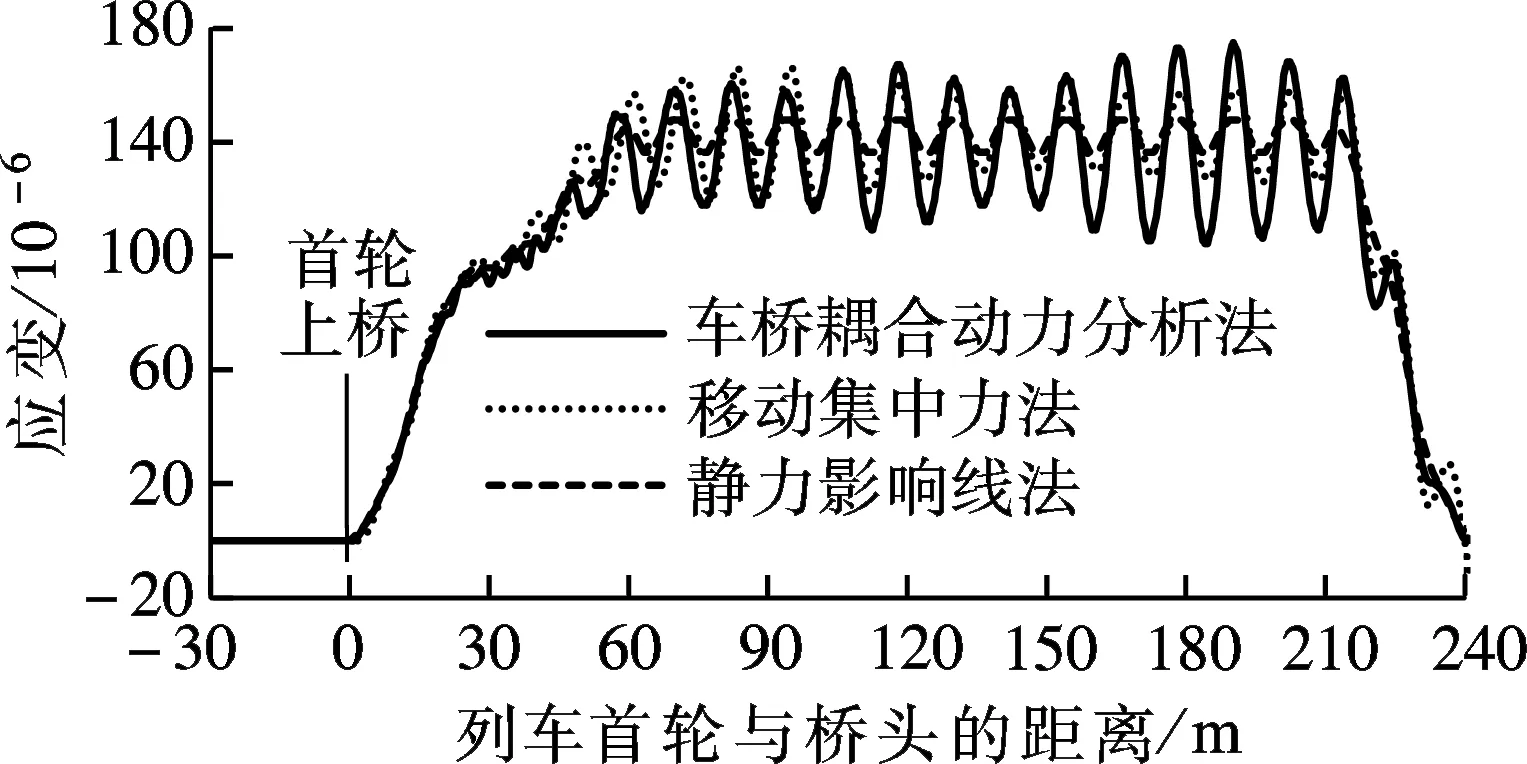
(b) Vres=210 km/h

图8为消振车速179和165 km/h下的桥梁应变响应．可以看出,消振车速下3种方法计算结果的差别相对较小．由于消振效应能够减小桥梁动力放大效应,移动集中力法与静力影响线法的应变曲线较为接近．

综上可知,共振条件下3种方法所得结果的差别较大,消振发生时差别则相对较小．

3 钢桥实例分析

3.1 工程概况及现场实测

本文研究的单线下承式钢桁梁桥位于京通铁路,为3跨连续梁结构,每跨长128 m．两片主桁高13.4 m,相距8 m．主桁节点间距8 m,全桥共分48个节间．桥梁主要杆件采用焊接型钢,钢材编号为16Mnq．这些杆件大多为工字形截面,少数为箱形截面,杆件之间通过高强螺栓连接．该桥使用明桥面,钢轨通过扣件与木枕相连,木枕则放置在采用工字形截面的2片纵梁之上．通过较为全面的现场静、动载试验,测量得到桥梁模态参数、挠度、振动及应力响应等,其中自振频率通过环境激励测试得到．桥梁1阶振型为横向振动,频率为1.04 Hz[18],1阶竖向振动的自振频率为1.55 Hz[18],可见该桥横向刚度相对较小．应力响应通过在选定的杆件上布置应变片测量得到,测试荷载为试验列车以及实际运营的客、货车．动应力测试杆件及应变片布置如图9所示．

(a) Vcan=179 km/h

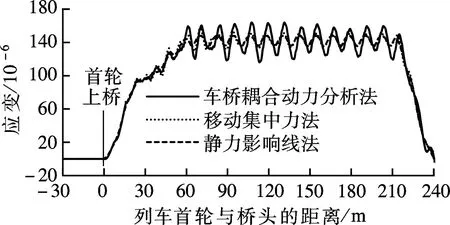
(b) Vcan=165 km/h

3.2 应力结果比较

进行应力响应数值计算前,采用ANSYS软件建立了该桥的有限元模型．各杆件均使用BEAM188单元模拟,单元截面形状及尺寸按照设计图纸确定．由于主要节点均采用高强螺栓进行连接,杆件之间假定为刚性连接．2个固定支座位于北京端,其余均为滑动支座．明桥面二期恒载按1 t/m 计,并折算成构件质量密度加以考虑．为便于移动集中力在2片纵梁上施加,划分纵梁单元时长度取为0.5 m．模型中总单元及节点数分别为2 761 和4 537．有限元模型如图10所示．由上述有限元模型得到的桥梁1阶横向、竖向自振频率分别为1.03和1.55 Hz,与实测横、竖向基阶振型的振动频率吻合．

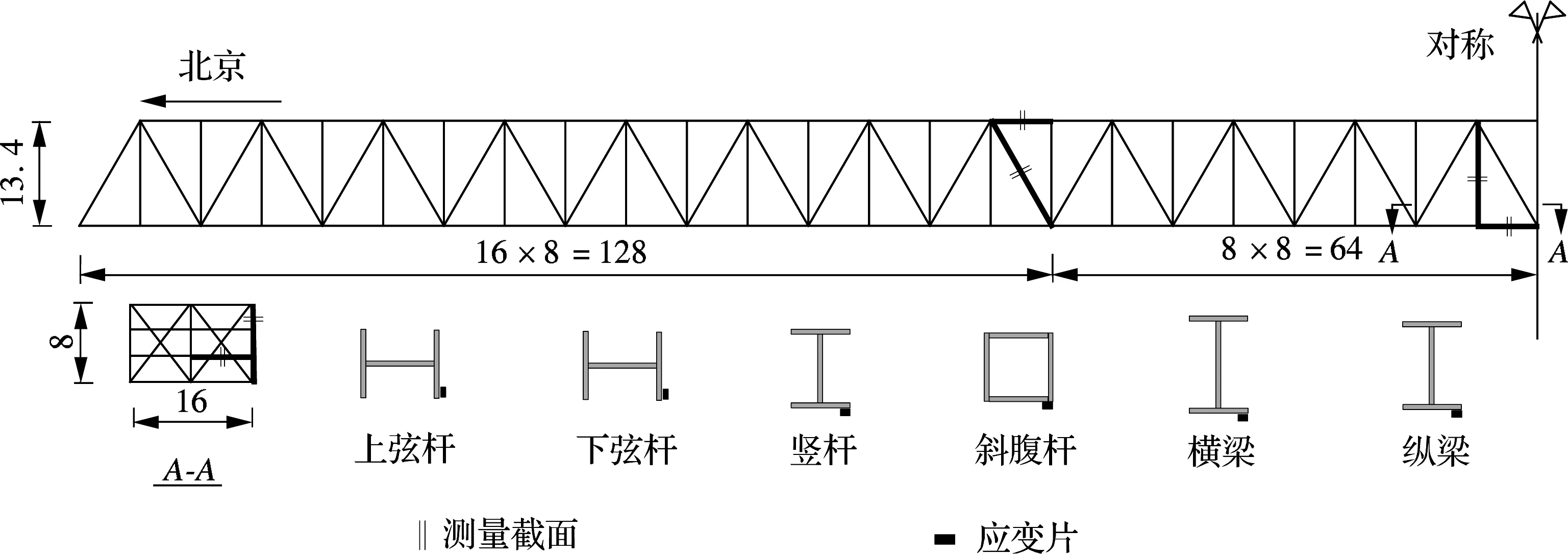
图9 测量杆件及应变片布置(单位:m)

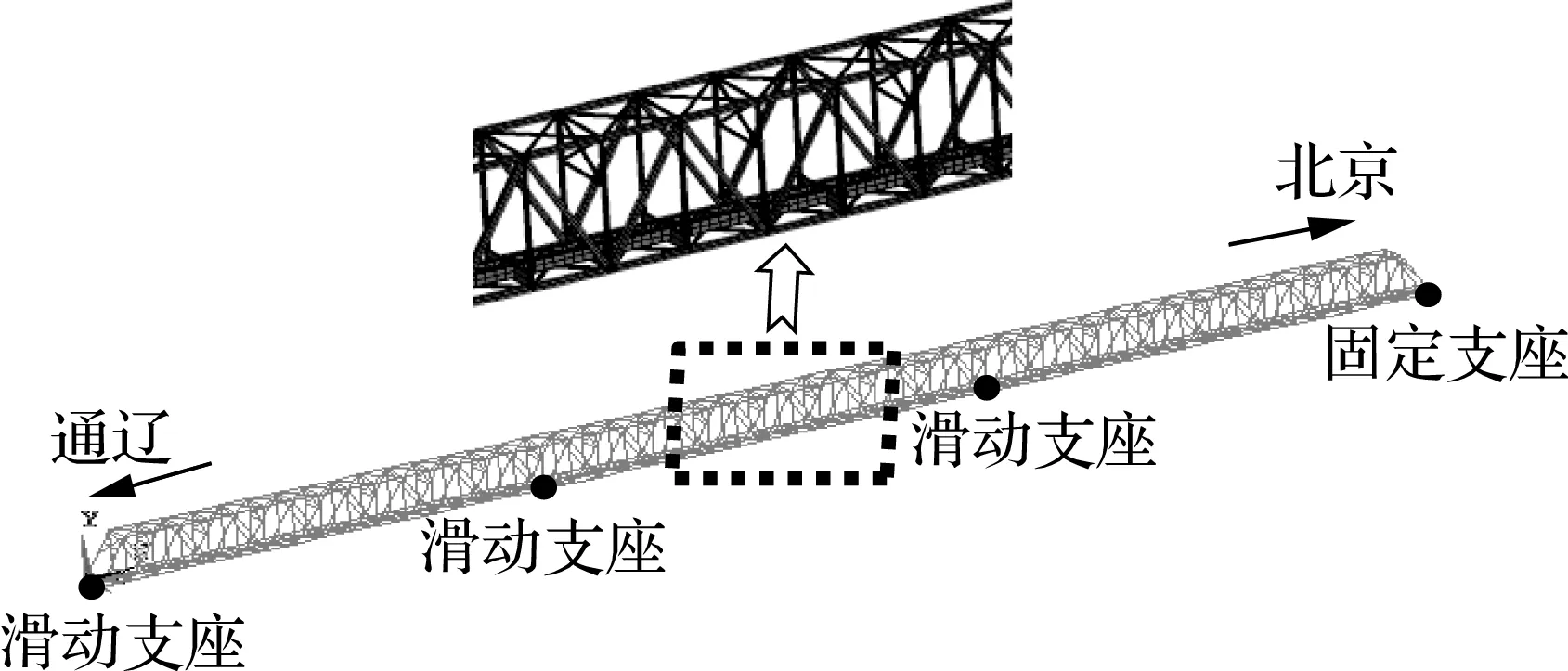
图10 下承式钢桁梁桥有限元模型

试验列车编组为2台DF4型机车牵引6辆C62型满载敞车及14辆C62型空车,荷载总长311 m．机车、重车及空车的轴重分别为23.0,20.6,5.6 t,作为静力影响线法及移动集中力法分析的荷载取值依据．列车以80 km/h的速度通过桥梁,预先布置的应变片记录了图9所示杆件在试验列车通过时的动应力时程．车桥耦合动力分析法中轨道不平顺样本根据美国5级谱生成．图11给出了移动集中力法、车桥耦合动力分析法及现场实测的动应力时程曲线．图中,应力符号约定受拉为正，受压为负．

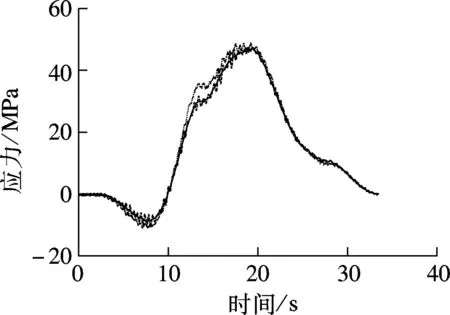
(a) 上弦杆

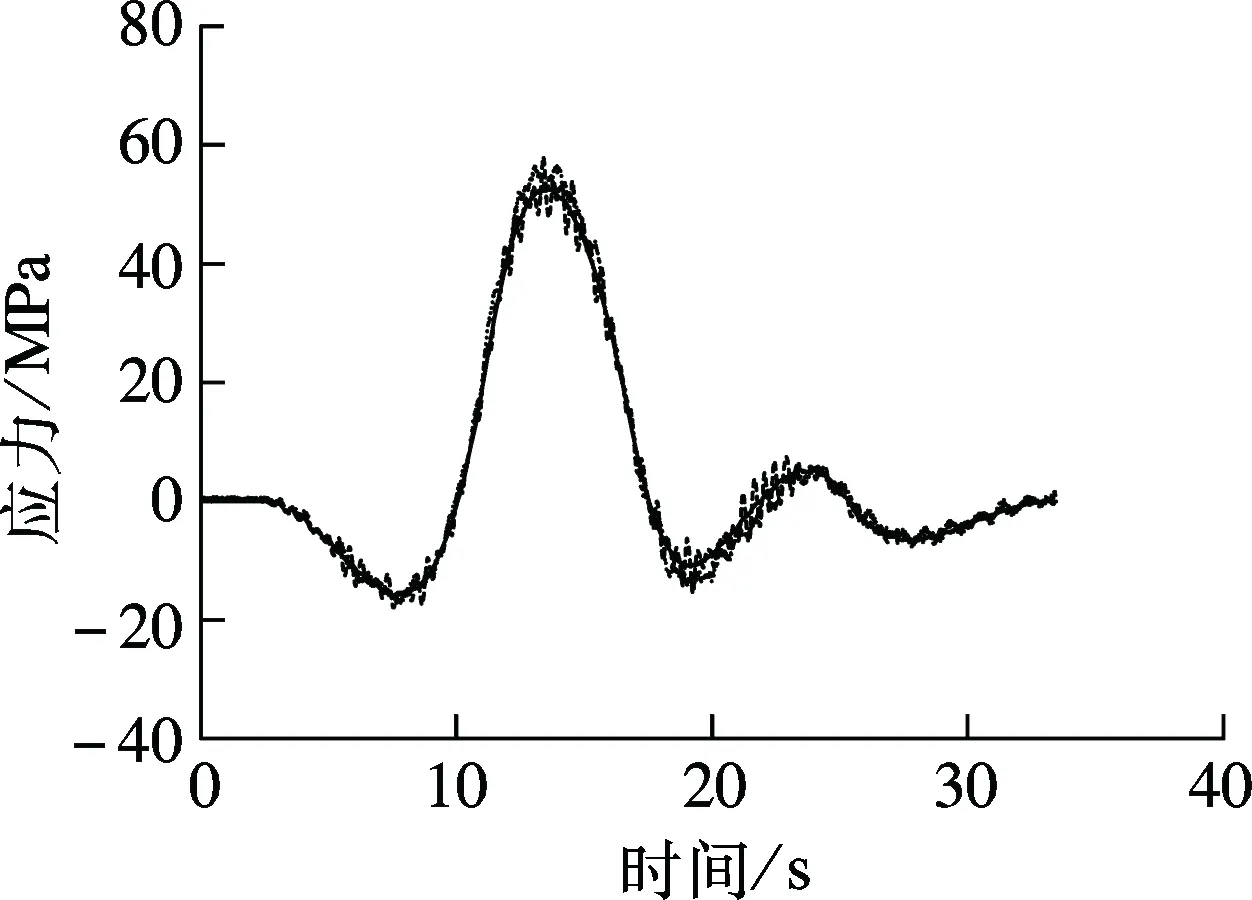
(b) 下弦杆

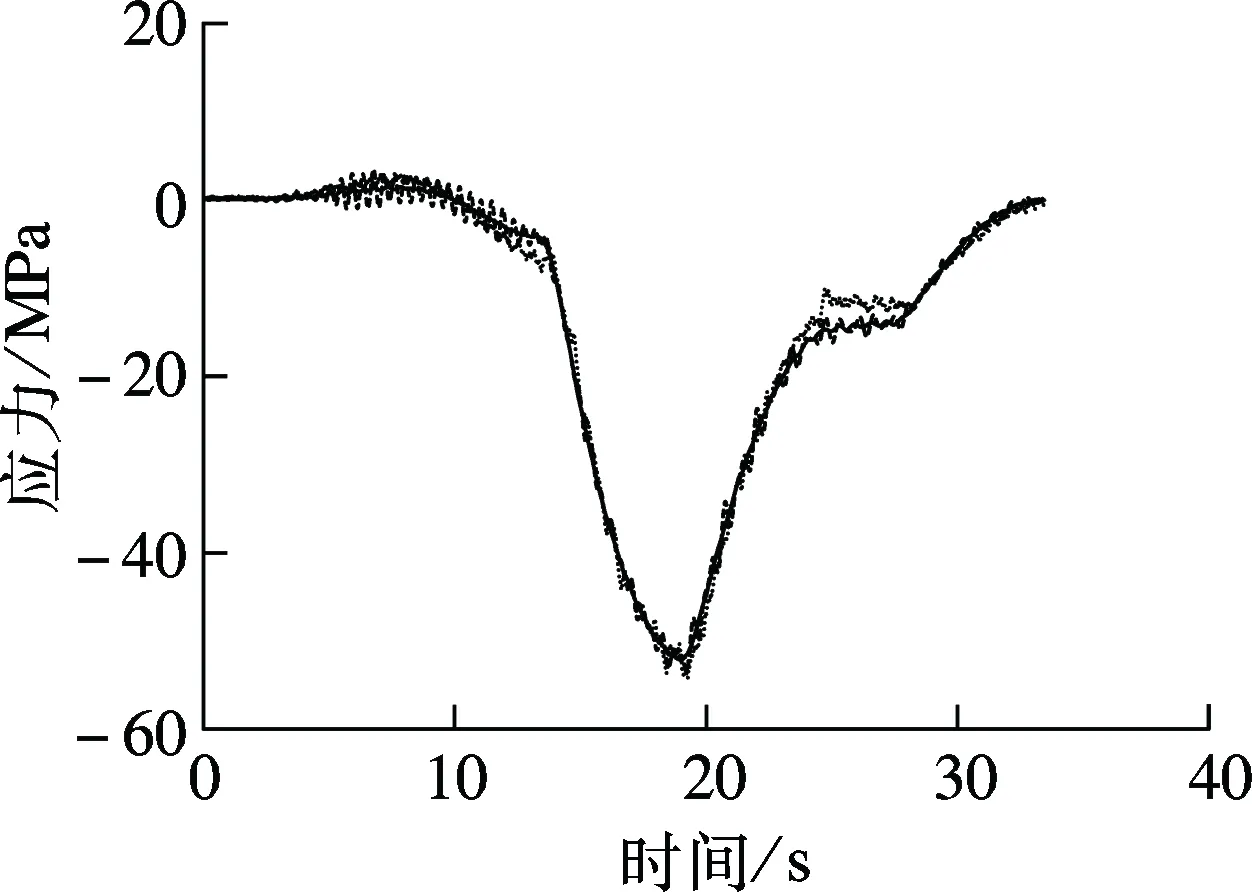
(c) 斜腹杆

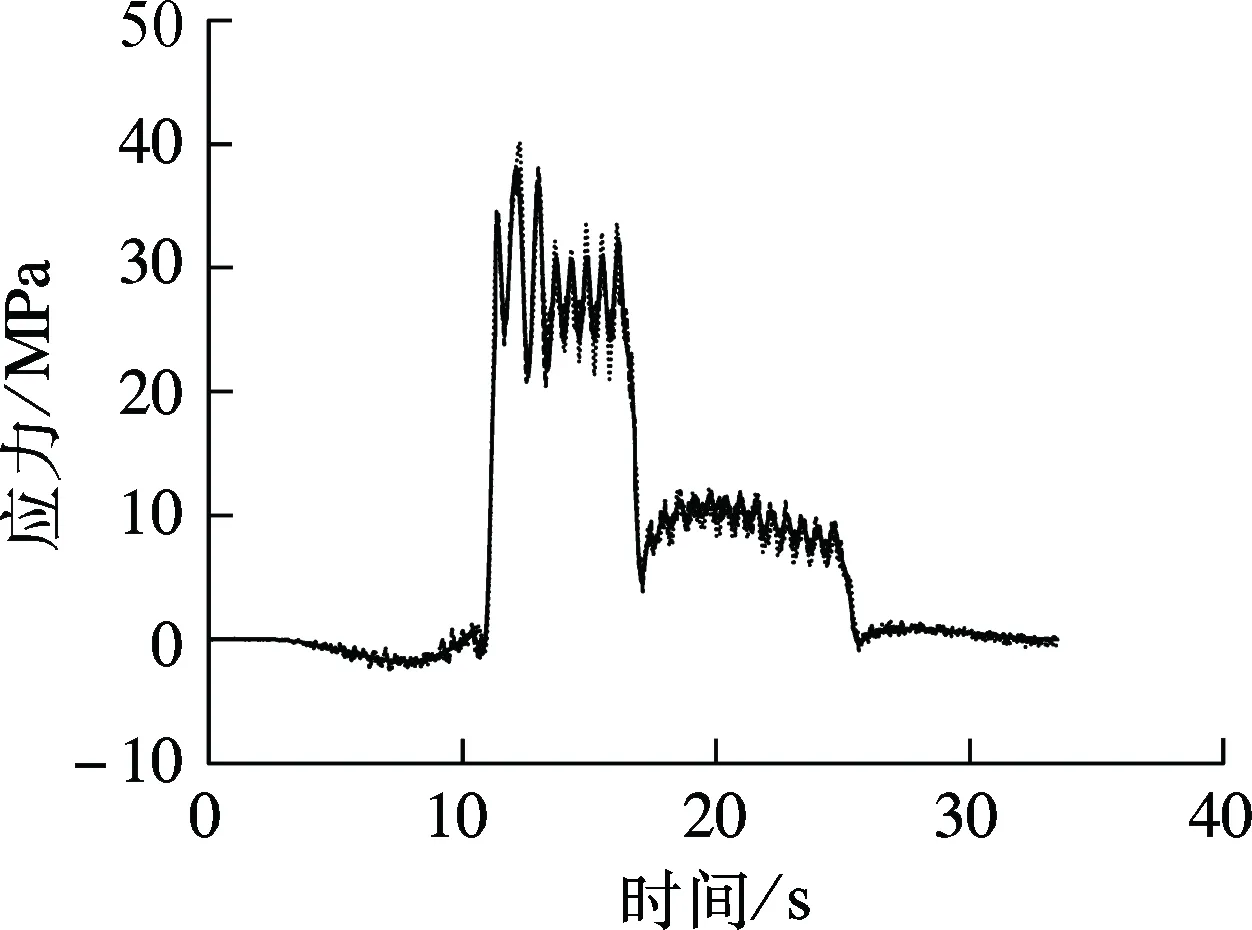
(d) 竖杆

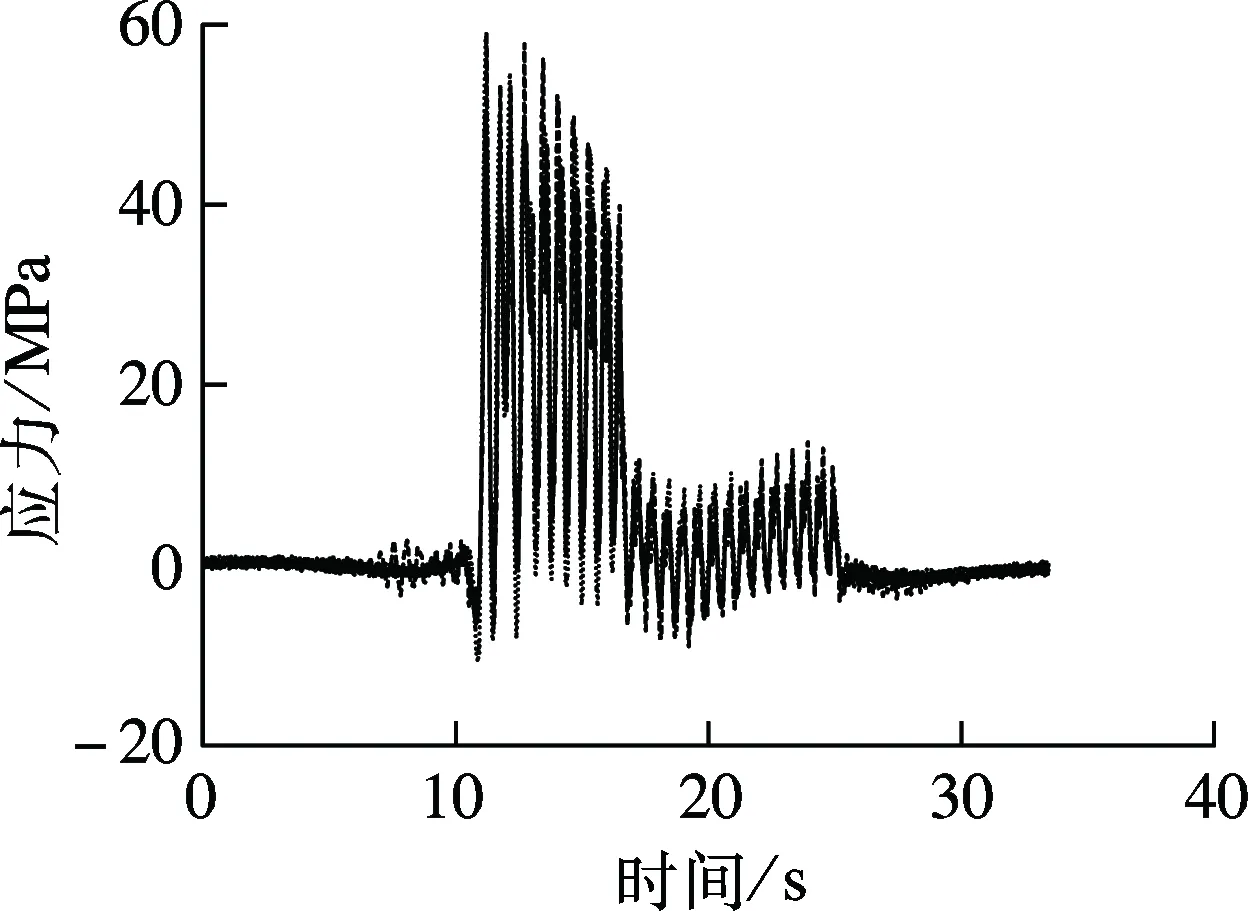
(e) 纵梁

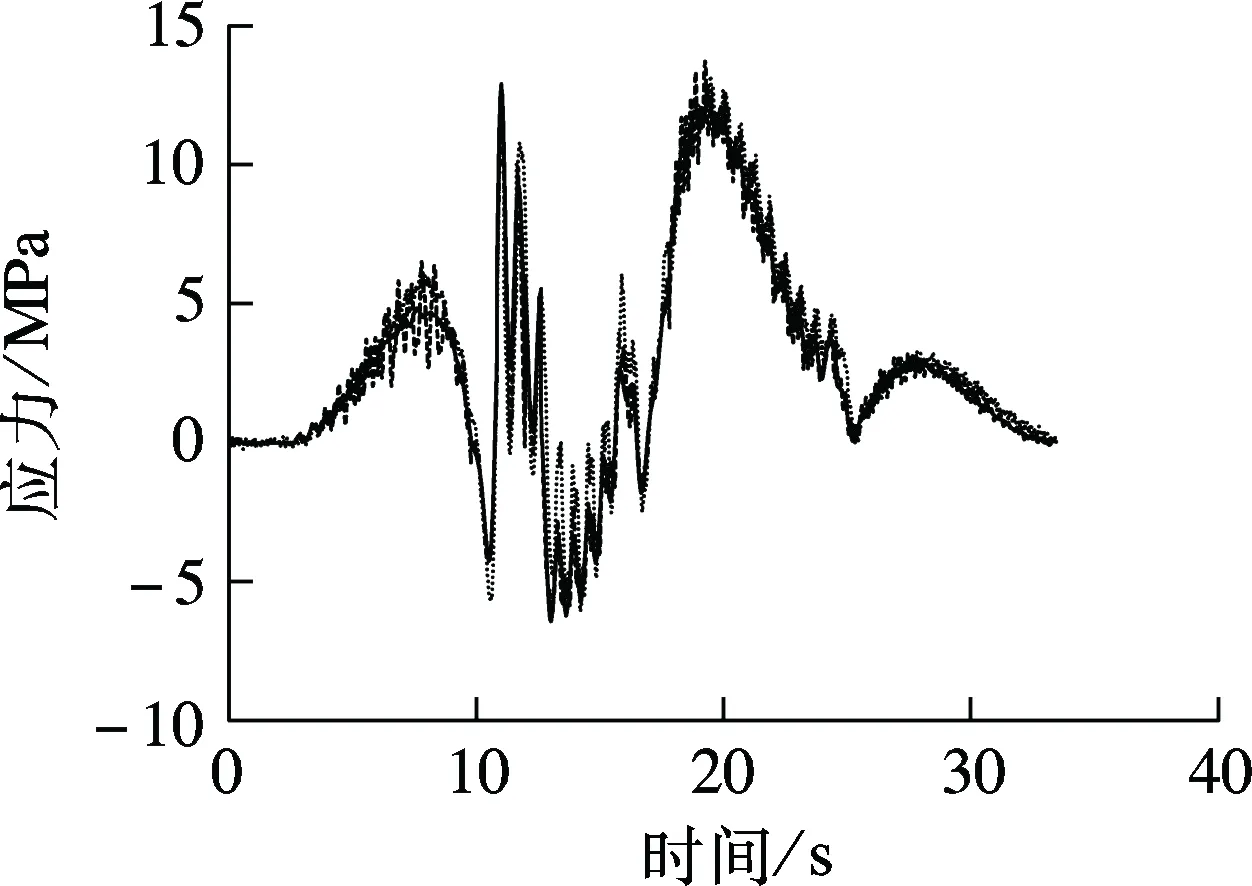
(f) 横梁

从图11可看出,采用车桥耦合系统模型所得各杆件动应力时程与实测结果接近,说明车桥耦合动力分析法能够较为精确地模拟列车过桥时桥梁杆件的应力历程．表1给出了最大应力(绝对值)计算值与实测值之间的差异百分数．其中,计算值与实测值差异百分数是指实测值和计算值的差值与实测值的比值．

由图11和表1可知,对于主桁杆件(如弦杆、腹杆等),移动集中力法的计算结果与实测应力值较为接近．由于该下承式钢桁梁桥跨度较大, 试验列车相对桥梁的质量较小,且车速较低,故列车、桥梁之间的整体耦合动力效应并不明显．因此,移动集中力法亦能较好地模拟主桁杆件的应力时程．对于承受列车局部加载作用的桥面系纵、横梁,其动力效应较为明显．移动集中力法与考虑车桥动力相互作用的耦合系统模型之间的差别较大,后者的计算结果能够更为真实地反映纵、横梁的应力历程．

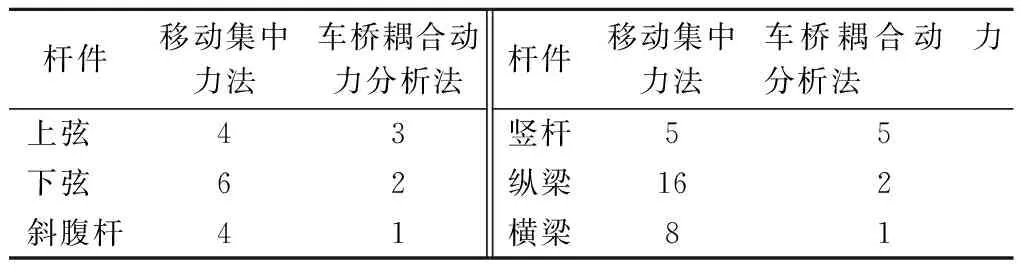
表1 最大应力计算值与实测值的差异百分数 %

3.3 横向振动影响

本文分析的下承式钢桁梁桥采用明桥面,钢轨通过放置于2片工字形纵梁上的木枕支撑．因此,列车轴重荷载通过钢轨、木枕等首先传至纵、横梁．此外,列车的水平向作用力将引起纵梁的横向(面外)弯曲振动．为研究其对杆件应力响应的影响,计算了不包含横向振动效应的纵梁动应力时程,并与图11(e)中的计算结果进行比较,结果见图12．

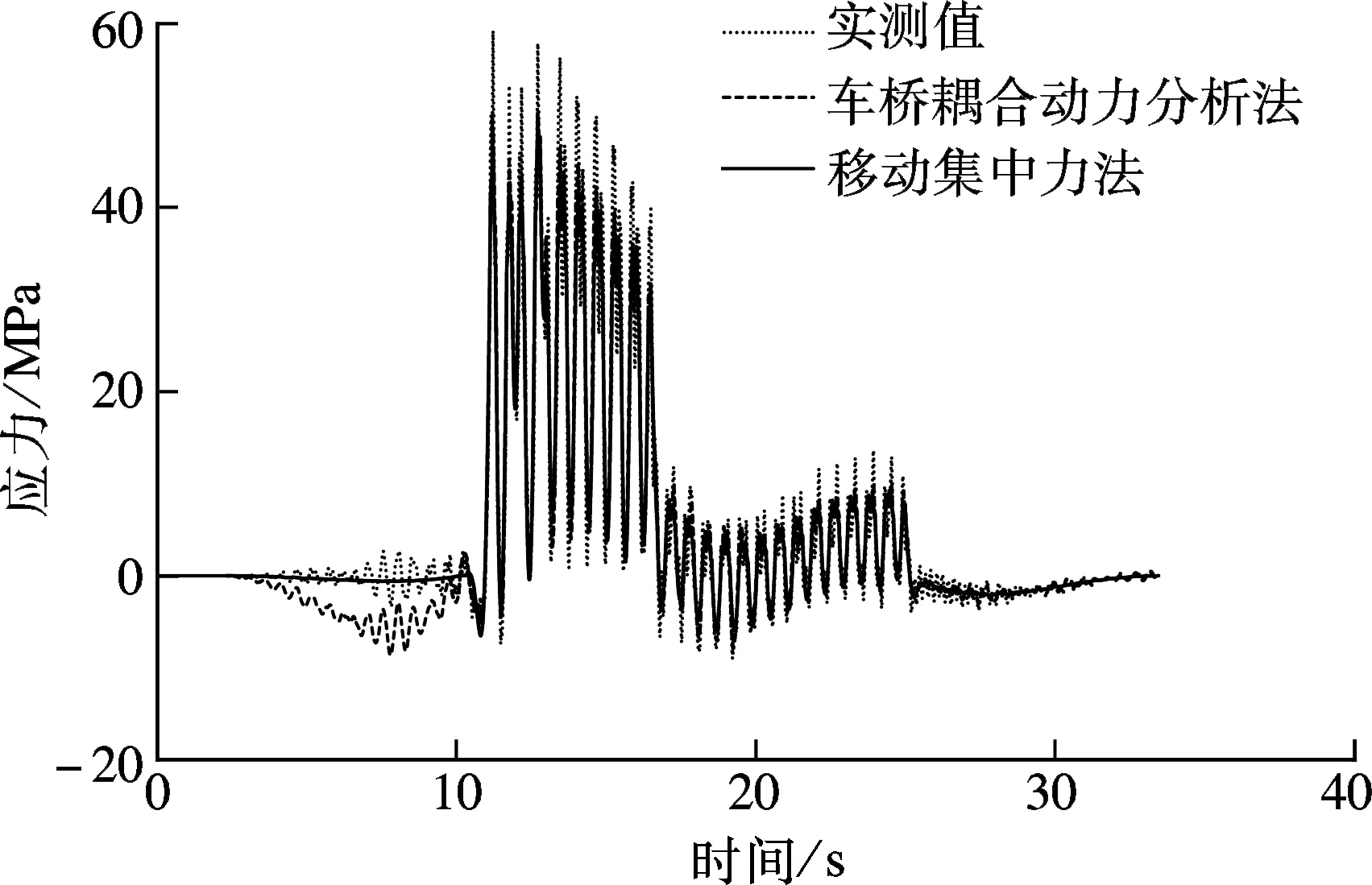
图12 横向振动对应力响应的影响

由图12可知,纵梁横向振动对其动应力响应的贡献较大．不考虑横向振动的贡献时,车桥耦合系统模型与移动力模型的计算结果较为接近,且均与实测应力相差较大．对于承受列车局部加载的构件或者横向刚度较低的桥梁,车桥动力相互作用可引起桥梁或构件较大的横向振幅,进而产生显著的应力响应．此时,横向振动对总应力响应的贡献不能忽略．静力影响线法及移动集中力法均无法考虑列车作用在桥梁水平方向上的力,其计算结果可能与真实的应力响应相差较大．

4 结论

1) 基于车桥耦合动力分析法所得的桥梁应力(应变)响应与现场实测数据符合较好,所分析的2座混凝土桥及钢桥具有代表性,证明该方法可用于准确计算列车作用下铁路桥梁的动应力响应．

2) 列车速度能够显著地影响桥梁的应力响应.同一车速下静力影响线法、移动集中力法和车桥耦合动力分析法所得的应力结果并不相同.共振发生时3种方法的计算结果相差较大,消振条件下三者区别减小．

3) 由列车水平方向作用力引起的桥梁或构件横向振动对应力响应的贡献不容忽视,静力影响线法和移动集中力法均无法考虑列车对桥梁的横向作用,其计算结果与真实的桥梁应力可能存在较大区别．

4) 基于车桥耦合动力分析法充分考虑了列车与桥梁的相互作用,并计入列车质量、轨道不平顺和横向振动等效应的影响,相比既有的静力影响线法和移动集中力法,能够更为真实地反映桥梁构件的应力历程．

总的来说,车桥耦合动力分析法具有计算精度上的优势．特别地,在高速、桥梁横向刚度较低或列车局部加载的情况下,静力影响线法和移动集中力法可能引起较大的误差,此时宜考虑采用车桥耦合动力分析法．

References)

[1]Nowack H, Schulz U. Significance of finite element methods (FEM) in fatigue analysis [C]//Fatigue’96:Proceedingsofthe6thInternationalFatigueConference. Berlin, Germany, 1996: 1057-1068.DOI:10.1016/b978-008042268-8/50052-6.

[2]British Standards Institution. Steel, concrete and composite bridges: Part 10: Code of practice for fatigue [S]. London: British Standards Institution, 1980.

[3]中铁大桥勘测设计院有限公司. TB 10002.2—2005 铁路桥梁钢结构设计规范 [S]. 北京:中国铁道出版社, 2005.

[4]British Standards Institution. Steel, concrete and composite bridges: Part 2: Specification for loads [S]. London: British Standards Institution, 2006.

[5]European Committee for Standardization. Actions on structures: Part 2: Traffic loads on bridges [S]. Brussels: European Committee for Standardization, 2003.

[6]American Railway Engineering Association (AREA). Manual for railway engineering [S]. Washington DC, USA: AREA, 1983.

[7]Imam B M, Righiniotis T D, Chryssanthopoulos M K. Probabilistic fatigue evaluation of riveted railway bridges [J].JournalofBridgeEngineering, 2008, 13(3): 237-244. DOI:10.1061/(asce)1084-0702(2008)13:3(237).

[8]Lippi F V, Orlando M, Salvatore W. Assessment of the dynamic and fatigue behaviour of the Panaro railway steel bridge[J].StructureandInfrastructureEngineering, 2013, 9(8): 834-848. DOI:10.1080/15732479.2011.625955.

[9]Zhou H, Liu K, Shi G, et al. Fatigue assessment of a composite railway bridge for high speed trains. Part Ⅰ: Modeling and fatigue critical details [J].JournalofConstructionalSteelResearch, 2013, 82: 234-245. DOI:10.1016/j.jcsr.2012.12.006.

[10]夏禾, 张楠. 车辆与结构动力相互作用 [M]. 北京: 科学出版社, 2005: 140-198.

[11]郭文华, 郭向荣, 曾庆元. 京沪高速铁路南京长江大桥斜拉桥方案车桥系统振动分析[J]. 土木工程学报, 1999, 32(3): 23-27. DOI:10.3321/j.issn:1000-131X.1999.03.004. Guo Wenhua, Guo Xiangrong, Zeng Qingyuan. Vibration analysis of train-bridge system for cable-stayed bridge scheme of Nanjing Yangtse Bridge on Beijing-Shanghai high speed railway [J].ChinaCivilEngineeringJournal, 1999, 32(3): 23-27. DOI:10.3321/j.issn:1000-131X.1999.03.004. (in Chinese)

[12]李小珍. 高速铁路列车-桥梁系统耦合振动理论及应用研究 [D]. 成都: 西南交通大学土木工程学院, 2000.

[13]高芒芒. 高速铁路列车-线路-桥梁耦合振动及列车走行性研究 [J]. 中国铁道科学, 2002, 23(2): 135-138. DOI:10.3321/j.issn:1001-4632.2002.02.024. Gao Mangmang. Studies on train-track-bridge coupling vibration and train performance on high-speed railway bridges [J].ChinaRailwayScience, 2002, 23(2): 135-138. DOI:10.3321/j.issn:1001-4632.2002.02.024. (in Chinese)

[14]李永乐, 强士中, 廖海黎. 风-车-桥系统空间耦合振动研究[J]. 土木工程学报, 2005, 38(7): 61-64,70. DOI:10.3321/j.issn:1000-131X.2005.07.012. Li Yongle, Qiang Shizhong, Liao Haili. 3D coupled vibration of wind-vehicle-bridge system[J].ChinaCivilEngineeringJournal, 2005, 38(7): 61-64,70. DOI:10.3321/j.issn:1000-131X.2005.07.012.(in Chinese)

[15]李慧乐, 夏禾, 张楠, 等. 基于车桥耦合动力分析的桥梁动应力计算方法 [J]. 中国铁道科学, 2015, 36(1): 68-74. DOI:10.3969/j.issn.1001-4632.2015.01.10. Li Huile, Xia He, Zhang Nan, et al. Calculation method for dynamic stress of bridge based on vehicle-bridge coupled dynamic analysis [J].ChinaRailwayScience, 2015, 36(1): 68-74. DOI:10.3969/j.issn.1001-4632.2015.01.10.(in Chinese)

[16]Xu Y L, Li Q, Wu D J, et al. Stress and acceleration analysis of coupled vehicle and long-span bridge systems using the mode superposition method[J].EngineeringStructures, 2010, 32(5): 1356-1368. DOI:10.1016/j.engstruct.2010.01.013.

[17]李慧乐, 夏禾, 郭薇薇. 简支梁在列车荷载下的共振与消振效应 [J]. 振动工程学报, 2014, 27(2): 172-179. DOI:10.3969/j.issn.1004-4523.2014.02.003. Li Huile, Xia He, Guo Weiwei. Effects of vibration resonance and cancellation for simple beams under train load [J].JournalofVibrationEngineering, 2014, 27(2): 172-179. DOI:10.3969/j.issn.1004-4523.2014.02.003.(in Chinese)

[18]北京铁路局工务处桥梁检定队. 京通线K83+743白河大桥常规检定评估试验报告 [R]. 北京: 北京铁路局工务处桥梁检定队, 2012.

Comparison of computation methods for stress response of bridges under train load

Li Huile1Xia He2Zong Zhouhong1

(1Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

To effectively analyze the train-induced stress responses of bridges, a comparative study on three computation methods for the stress responses of bridges under train loads, namely, the train-bridge coupled vibration analysis method, the static influence line method, and the moving concentrated load method is performed. The stress responses of two typical railway bridges, a concrete simply-supported T beam bridge and a steel through truss girder bridge, are analyzed through the three methods. The computation results from various methods are compared and analyzed by using the data measured at the bridge sites. The influences of the train speed and the bridge lateral vibration on the stress results are investigated. The results show that the train speed significantly affects the bridge stress responses. Considerable differences are found in the computation results obtained from the three methods when the vibration resonance occurs, while the differences are reduced under the condition of the vibration cancellation. The contributions of the lateral vibrations of the bridges or the components induced by the horizontal train loading to the stress responses cannot be neglected. The train-bridge coupled vibration analysis method can more truly reflect the dynamic stress histories, and especially has the advantages of calculation accuracy in the cases of high speed, low lateral bridge stiffness, or local train loading. The results can provide references for the engineering applications of three different computation methods.

stress analysis; train-bridge coupled vibration; field test; train speed; lateral vibration

10.3969/j.issn.1001-0505.2017.03.027

2016-09-22. 作者简介: 李慧乐(1987—)，男，博士，讲师，huile.li@seu.edu.cn.

国家重点基础研究发展计划(973计划)资助项目(2013CB036203)、“十二五”国家科技支撑计划资助项目(2014BAK11B04)、国家自然科学基金资助项目(51528802).

李慧乐,夏禾,宗周红.列车作用下桥梁应力响应计算方法比较[J].东南大学学报(自然科学版),2017,47(3):576-583.

10.3969/j.issn.1001-0505.2017.03.027.

U448.13

A

1001-0505(2017)03-0576-08