基于拥堵辨识的城市路网优化模型

诸 云 王建宇 高宁波 杨 莹

(南京理工大学自动化学院, 南京 210094)

基于拥堵辨识的城市路网优化模型

诸 云 王建宇 高宁波 杨 莹

(南京理工大学自动化学院, 南京 210094)

为了改善道路交通拥堵状况,在分析城市道路网络交通拥堵博弈关系的基础上,建立了以交通拥堵程度为下层决策目标、经济费用为上层决策目标的城市路网优化双层规划模型.上层模型以管理者对路网运营成本投入最优为目标,下层模型力求路网的出行效率最高,针对该模型提出遗传算法求解流程.以南京市某区域道路网络为例进行分析研究,结果表明:优化后的路网效能优于原始路网, 路网运行速度、服务水平均有提升;维护费用及延误均下降.双层规划模型主要针对路网中道路等级低、饱和度高的路段进行改造升级,在一定投入费用范围内实现路网交通拥堵与投入费用的最优平衡关系,能够为路网优化决策提供参考.

交通拥堵;路网优化;双层规划;遗传算法

近年来,国内城市机动车保有量增势迅猛,交通资源和交通需求在时间和空间上的矛盾日益突出,交通拥堵已经成为各大中城市亟待解决的问题.从已有成果来看,交通拥堵研究主要集中在城市交通拥堵管理政策、城市道路网络出行路径优化和城市道路网络优化等方面.陆化普[1]分析了城市交通拥堵形成机理,归纳总结了交通拥堵的对策体系.曾鹦等[2]从博弈论的角度定义了拥堵成本的概念,证明了拥堵收费的合理性.而发达国家和地区所采取的系列治理方案主要涉及到行政限制性政策、拥堵收费性政策和外延支撑性政策[3].徐丽丽等[4]利用路径诱导信息建立了交通出行选择的双层规划模型,得出不同路径诱导信息对出行者影响的范围.宋留勇等[5]通过分析路段出行时间的波动特性,建立了基于时间可靠度的交通路网出行路径的简化模型.Friesz等[6]梳理了非传统方程在解决城市道路动静态网络优化中的研究成果.Karoonsoontawong等[7]建立了基于通行能力的一般双层规划的城市网络优化模型.Mathew等[8]提出了利用双层规划模型优化乡村道路网络布局.Gao等[9]提出了基于环境目标的城市网络优化双层规划模型,设计了城市网络双层规划优化算法,总结了城市交通网络设计问题中双层规划模型及其运用.

综上可知,近年来城市交通拥堵在管理政策、对策等方面取得了丰富的研究成果.但是国内采用的拥堵收费、常发拥堵路段改造等措施都只考虑交通拥堵的表象,缺乏基于产业空间布局、城市管理以及区域协调发展等方面的综合考察,致使治堵对策分析存在局限性和片面性.本文从城市资源和拥堵治理的博弈关系出发,通过对城市交通拥堵的辨识研究,将城市交通拥堵问题分为上层管理者对拥堵治理的投入约束和下层出行者对路网出行效率诉求2个层面,实现治理投入成本与城市拥堵状态的最优平衡目标.

1 城市路网交通拥堵辨识的博弈机理

出行交通量集中于某条道路并超过道路容量时,就会造成道路交通拥堵.更为严重的是,城市路网衔接紧密,局部拥堵易引发路网交通瘫痪危机.交通拥堵问题属于复杂的系统工程问题,在对交通拥堵进行准确辨识的前提下,交通拥堵博弈分析有助于明确拥堵影响边界,为交通拥堵的治理提供决策依据.

1.1 交通拥堵博弈关系

不同的交通流量与路网容量的对比关系产生了2种不同的交通运行状态,如图1所示.交通拥堵对城市路网的影响主要集中在2个方面:① 降低路网的机动性能;② 增加路网的基础费用.为保证交通畅通应从基础设施投入和管理规划2方面考虑.

路网建设后期投入包括基础维护以及优化投入.交通拥堵导致基础维护费用增加,而基础维护费用的减少又说明交通趋于顺畅;为了保证交通顺畅需要增加优化投入,交通拥堵又说明优化投入不足.因此,如何在城市道路网络建设后期投入与交通运行状态之间取得最优平衡,属于典型的博弈问题.

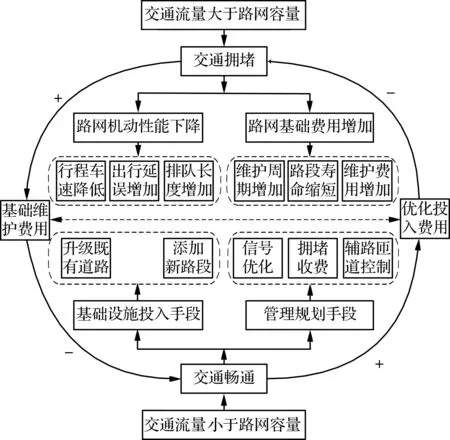
图1 城市道路网络交通拥堵博弈关系

1.2 拥堵辨识的指标体系

从空间分布来看,城市交通拥堵可划分为点、线、面3个相互影响的层面进行辨识.因此,采用出行速度、平均延误以及拥堵指数分别作为路段、交叉口以及路网的交通拥堵判别指标,并且定义路网维护费用、改造费用以及附加费用作为交通拥堵的经济评价指标,各个指标的计算过程[10]如下.

1) 平均出行速度的函数关系式为

(1)

式中,v平均出行速度;vab为路网第a条路段第b辆车的通行速度;N为路段总数;M为每条路段的车辆通行总数.

2) 平均出行延误的函数关系式为

(2)

式中,Δt为平均出行延误时间;ta为路网每条包含交叉口路段的期望出行时间,即路段交叉口耗时为0;tab为第a条路段第b辆车的实际出行时间.

3) 路网拥堵指数的函数关系式为

(3)

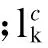
4) 路网维护费用的函数关系式为

(4)

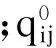
5) 拥堵附加费用的函数关系式为

(5)

(6)

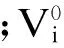
6) 道路改造费用的函数关系式为

(7)

f(lij,di,wij)=lijdiwij

(8)

式中,e为路网道路升级费用,取值为道路面积和单位面积道路升级费用的复合函数f(lij,di,wij);di为道路从支路到次干路、次干路到主干路、主干路到快速路3种升级类别的道路单位长度升级费用;pi为第i等级道路中需要升级的路段数量;lij为第i等级道路中第j条路段需要升级的长度.

2 城市路网交通拥堵的优化模型

城市交通拥堵路网优化双层规划模型的下层决策变量是交通拥堵状态,上层决策变量是交通流量,通过对该模型的求解得到城市道路网络维护成本费用和城市交通拥堵状态之间的最优平衡关系.

2.1 双层规划模型

城市交通拥堵路网优化的数学模型中,上层目标函数F(Vij)为整个路网的运行成本费用以及道路升级费用之和,决策变量为路网上各个路段的交通流量Vij.下层目标函数G(ti)以城市道路网拥堵程度为目标,决策变量为路网上每个路段的出行耗时ti.Vij与ti互相作用.

1) 上层规划模型

minF(Vij)=q0+q+e=

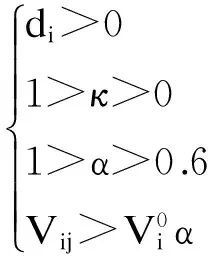
(9)

2) 下层规划模型

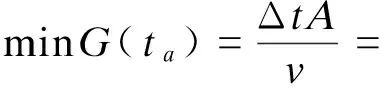
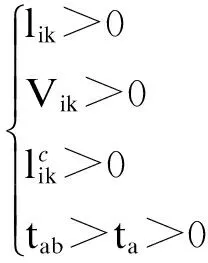
(10)

2.2 优化模型求解

双层规划模型属于多目标约束函数模型,遗传算法对非线性问题具有强的空间搜索能力,被广泛运用于多目标规划问题的求解.因此,采用遗传算法求解双层规划[11],具体过程如下.

1) 遗传算子设计

① 解空间数值化.采用0-1关联矩阵(0为端点间有路段,1为端点间无路段)表示路网的空间结构,采用0-4效用矩阵表示路网属性,其中,0为端点间无路段;1为支路;2为次干路;3为主干路;4为快速路.

② 适应度函数选择.利用遗传算法寻优的过程中,需要以某一函数作为优化目标和搜索方向.在城市道路网络交通拥堵双层规划模型中可分别采用式(9)和(10)作为上、下层遗传算法的目标函数.

③ 交叉和变异方法.交叉运算是遗传算法区别于其他算法的重要特征,本文采用单点交叉算子作为交叉方法;变异操作是提高全局搜索能力的有效步骤,本文采用的变异策略是选取2个任意基因位,然后将基因交换的方法.

④ 确定其他相关参数.遗传算法中涉及的其他参数还包括群体规模Ns、交叉概率Pc(经验取值范围为0.40～0.99)、变异概率Pm(经验取值范围为0.001～0.100)等,这些参数均可通过经验取值方法确定.

2) 规划模型空间寻优

① 上层规划初始化和编码.在上层规划的界限约束上随机生成N0个初始路网(N0≥1),设定上层最优循环最大迭代次数N1,将路网转换成为数值化矩阵.

② 路网交通运行参数仿真.将上层规划中释放的可行路网进行仿真,得到包括路网交通流量、路段平均运行速度等路网交通参数.

③ 下层规划函数寻优计算.利用步骤②的参数计算路网下层规划的目标函数,并进行适应度评价,根据评价排序结果从高到低进行选择、交叉、变异操作,得到最优的路网结构,并返回到上层规划模型中.

④ 上层规划解空间更新.对上层规划的解空间根据目标函数进行适应度评价,排序后剔除适应度值低的解，保留适应度高的解;对解空间选择、交叉、变异,将变异后的种群作为新一代种群,重复步骤②.

⑤ 终止运算与条件.如果当前上层规划外循环迭代次数s达到最大迭代次数N1，或者当上层规划的解空间无法进行更新,则停止,将当前的路网及其交通流参数作为双层规划的最优解，记录并输出，见图2.

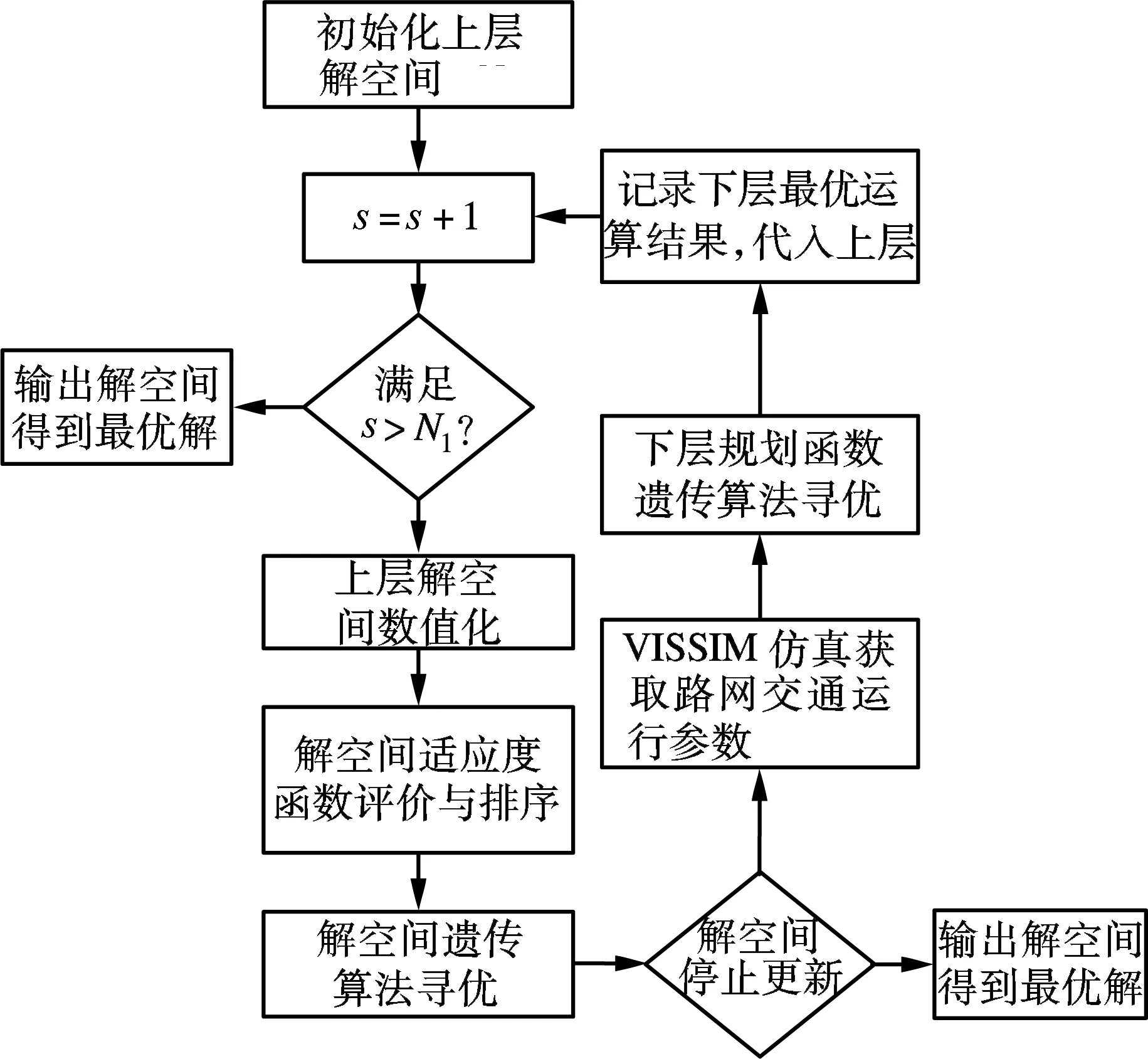
图2 基于遗传算法的双层规划求解流程

3 仿真分析

以南京市某一区域路网为例,分析上述模型的可行性.该路网外围由13条快速路组成,内部由10条主干路以及8条次干道组成,路网结构如图3(a)所示.

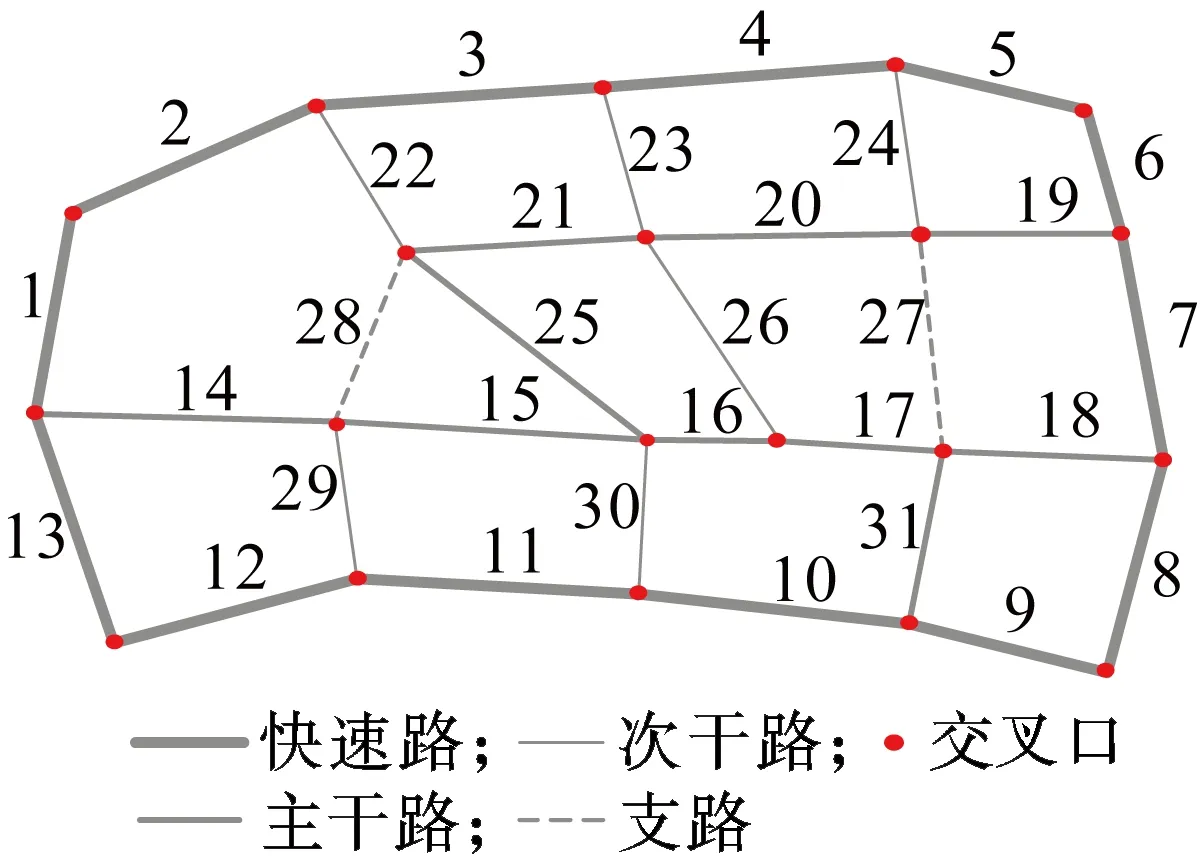
(a) 优化前

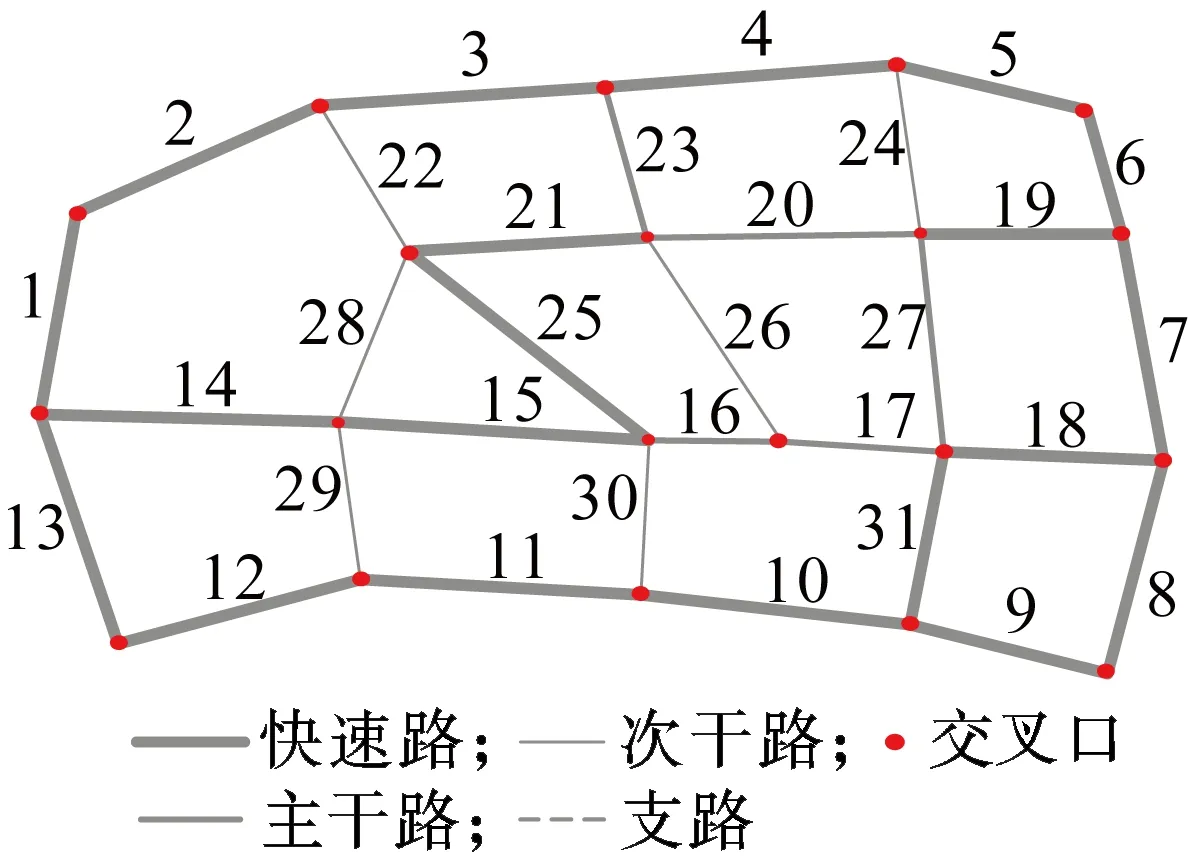
(b) 优化后

3.1 参数界定

为对模型进行求解,需要进一步确定各参数的设定值.其中,路网中不同等级道路的维护费用和升级费用数据见文献[12],课题组对该路网的路段等级、道路长度、道路交通流量和道路通行能力等进行了为期1周的调查,并根据估算得到不同等级道路的最大通行能力,遗传算法中选择概率和变异概率分别设定为0.80和0.05,终止迭代数设置为100,选择模式和交叉模式分别为轮盘赌方式和单点交叉方式,具体见表1.

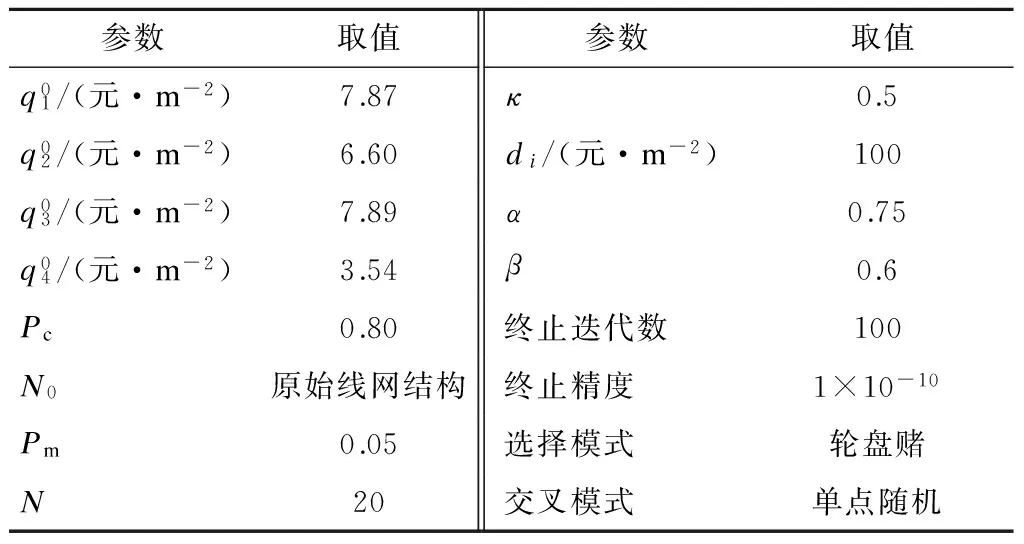
表1 南京市某道路网络参数信息

3.2 模型求解

利用Matlab(R2012)对建立的双层规划模型进行编程求解[13],将路网中31个路段设置为因变量,每个变量包含道路长度、道路等级、交通流量、平均行程车速4个变量,经过反复调试,得到数值仿真结果.

模型求解的演化过程可分为3个阶段:① 从第0代到第20代,种群变异速度较快,适应度值下降速度快,空间寻优效果明显;② 从第20代到第50代,种群变异速度开始降低,适应度值开始收敛;③ 从第20代到第100代,适应度值收敛在3.73×105,得到路网的最优解向量、优化后路网空间结构,如图3(b)所示.

通过对比优化前后的路网可知,优化路网在原始路网基础上将路段14、路段15以及路段18等主干道升级为快速路,路段23由次干路升级为主干路,路段27和路段28由支路分别升级为次干路和主干路,总升级费用为442.86万元.由表2对比发现,所有升级的道路中最大饱和度达到0.990,最小饱和度为0.769,平均路段饱和度为0.892,说明升级的路段均处于交通较为拥堵的状态,选择对这些道路升级,从一定程度上说明模型优化的可靠性.

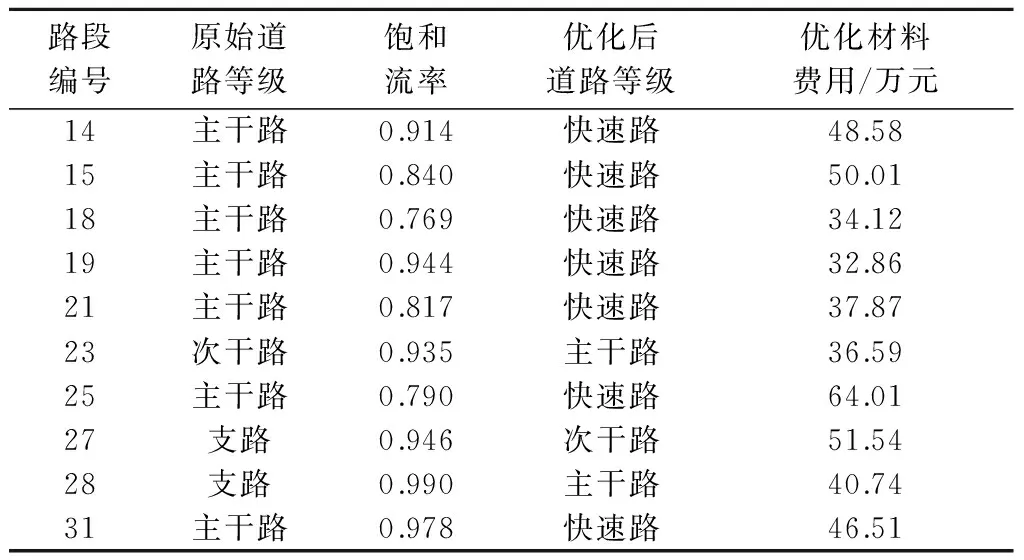
表2 城市道路网络优化变动情况

3.3 对比分析

为检验城市道路网络交通拥堵双层规划模型(式(3)和(4))的有效性,将已优化路网和原路网在VISSIM中建立模型进行仿真,采用节点控制和分散采集的模式获取优化前后路网各路段在仿真过程中的平均出行速度、平行出行时间延误以及拥堵状态等交通参数,结果如表3所示.

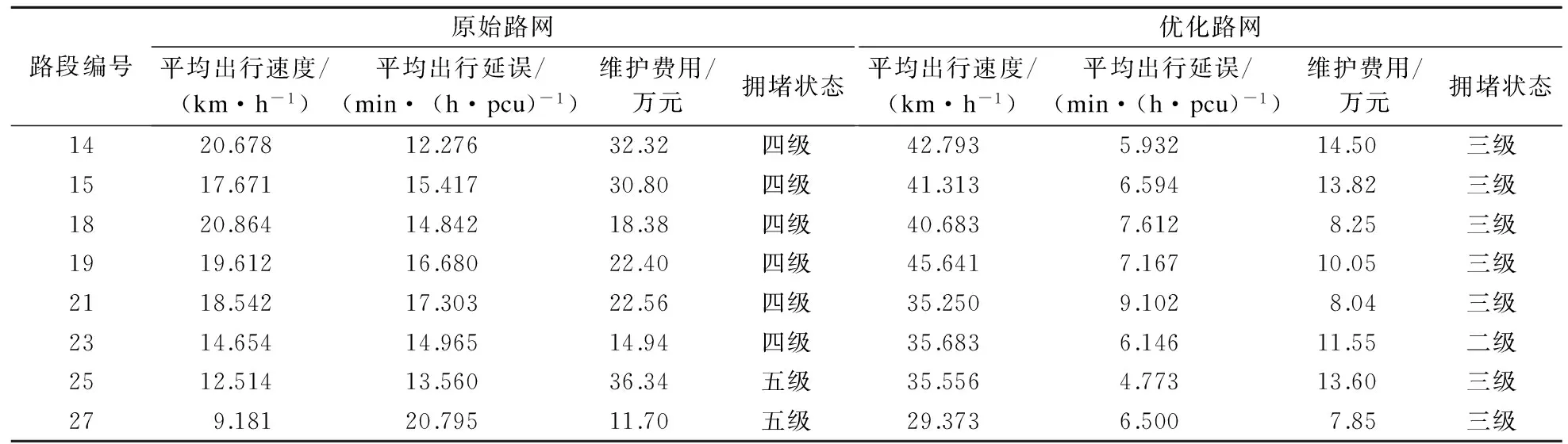
表3 基于VISSIM的南京市某路网优化前后部分仿真结果对比

3.4 路段服务水平分析

路网中优化后的路段服务水平与原始路网中路段相比,主要有如下特点:

① 运行速度增加.优化后路段的平均出行速度达到[30 km/h,55 km/h]区间,原始路网中未优化路段的平均出行速度位于[10 km/h,25 km/h]区间,提升道路等级后,相应道路的运行速度提升明显.

② 延误时间降低.原始路网中未优化的路段平均延误位于[10 min/(h·pcu),20 min/(h·pcu)]区间,在优化路网中,相应路段的出行延误降低到[5 min/(h·pcu),10 min/(h·pcu)]区间.

④ 维护成本降低.优化后路段的维护费用(基础道路维护费用和拥堵附加费用之和)位于[5万元,15万元]区间,原始路网中对应未优化的路段维护费用位于[15万元,35万元]区间.

⑤ 服务水平提高.优化后路段的拥堵服务水平位于[二级,三级]区间,原始路网中相应路段的拥堵服务水平位于[四级,五级]区间.

3.5 路网综合性能分析

为对优化路网进行性能分析,采用经济性能指标和机动性能指标作为路网性能评价指标.优化前后的路网性能指标对比如表4所示.

表4 优化前后路网交通性能对比

4 结语

本文从城市道路网络性能和投入费用2个方面分析了城市道路网络交通拥堵博弈关系,运用平均出行速度、平均出行延误、拥堵指数、道路维护费用等指标作为城市道路网络交通拥堵的博弈指标.在此基础上,建立了下层决策变量是交通拥堵状态、上层决策变量是交通流量的城市道路网络交通拥堵双层规划模型,提出了基于遗传算法的求解流程.以课题组对南京市某区域路网的调查数据进行模型参数标定,然后在Matlab中对双层规划模型进行求解,优化结果表明双层规划模型主要针对路网中道路等级低、饱和度高的路段进行改造升级.为分析优化路网和原始路网之间的路网性能,在VISSIM中建立路网模型并进行了仿真分析,结果表明优化路网在平均速度、出行延误等方面均优于原始路网.

References)

[1]陆化普.城市交通拥堵机理分析与对策体系[J].综合运输,2014(3):10-19. Lu Huapu. Congestion mechanism analysis and countermeasures system of urban traffic [J].ComprehensiveTransportation, 2014(3):10-19. (in Chinese)

[2]曾鹦,李军.合作博弈视角下城市道路交通拥堵收费研究[J]. 运筹与管理,2013,22(1):9-14.DOI:10.3969/j.issn.1007-3221.2013.01.002. Zeng Ying, Li Jun. Research about charge for traffic congestion of urban roads under perspective of cooperation. [J].OperationsResearchandManagementScience, 2013, 22(1):9-14. DOI:10.3969/j.issn.1007-3221.2013.01.002. (in Chinese) [3]赵蕾.城市交通拥堵治理:政策比较与借鉴[J].中国行政管理,2013,335(5):82-85. Zhao Lei. Management of urban traffic congestion: Countermeasures comparison and reference research[J].ChineseJournalofManagement, 2013,335(5): 82-85. (in Chinese)

[4]徐丽丽,邵春福.路径信息诱导的双层规划模型[J].交通运输工程学报,2007,7(5):15-21.DOI: 10.3321/j.issn:1671-1637.2007.05.020. Xu Lili, Shao Chunfu. Bi-level programming model of path information induction [J].JournalofTrafficandTransportationEngineering, 2007,7(5):15-21. DOI: 10.3321/j.issn:1671-1637.2007.05.020. (in Chinese)

[5]宋留勇, 王锐, 周永旺. 动态城市交通网络优化模型研究及算法设计[J]. 测绘科学, 2011, 36(1):134-136. Song Liuyong, Wang Rui, Zhou Yongwang. Network optimization model and algorithm design of urban traffic [J].ScienceofSurveringandMapping, 2011, 36(1):134-136. (in Chinese)

[6]Friesz T L, Shah S. An overview of nontraditional formulations of static and dynamic equilibrium network design[J].TransportationResearchPartB:Methodological, 2001, 35(1): 5-21. DOI:10.1016/s0191-2615(00)00002-3.

[7]Karoonsoontawong A, Waller S T. Integrated network capacity expansion and traffic signal optimization problem: Robust bi-level dynamic formulation [J].NetworksandSpatialEconomics, 2010, 10(4): 525-550.

[8]Mathew B S, Isaac K P. Optimisation of maintenance strategy for rural road network using genetic algorithm [J].InternationalJournalofPavementEngineering, 2014, 15(4): 352-360. DOI:10.1080/10298436.2013.806807.

[9]Gao Z, Wu J, Sun H. Solution algorithm for the bi-level discrete network design problem [J].TransportationResearchPartB:Methodological, 2005, 39(6): 479-495. DOI:10.1016/j.trb.2004.06.004.

[10]郑淑鉴,杨敬锋. 国内外交通拥堵评价指标计算方法研究[J]. 公路与汽运, 2014,6(1): 57-61. DOI: 10.3969/j.issn.1671-2668.2014.01.016. Zheng Shujian, Yang Jingfeng. The research on traffic congestion evaluation index at home and abroad[J].Highway&AutomotiveApplications, 2014, 6(1): 57-61.DOI: 10.3969/j.issn.1671-2668.2014.01.016.(in Chinese)

[11]赵志刚, 王伟倩, 黄树运. 基于改进粒子群的双层规划求解算法[J]. 计算机科学, 2013, 40(11a): 115-119. Zhao Zhigang, Wang Weiqian, Huang Shuyun. Bi-level programming algorithm based on improved particle swarm[J].ComputerScience, 2013, 40(11a): 115-119. (in Chinese)

[12]胡启洲,叶茂,邓卫.城市路网交通拥堵态势监控的测度理论方法[M].北京:科学出版社, 2013:8-23.

[13]张德丰.MATLAB/Simulink建模与仿真实例精讲[M].北京:机械工业出版社, 2010:56-76.

Urban traffic congestion optimization model based on bi-level programming

Zhu Yun Wang Jianyu Gao Ningbo Yang Ying

(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

To improve the situation of road traffic congestion, based on the analysis of the game relationship of urban road network traffic congestion, the lower decision-making objectives for traffic congestion level were established, the economic costs take the upper decision-making objectives of the urban road network optimization as a bi-level programming model. The upper model aimed at the optimization of the cost in which operators invest for road network operation. The lower model optimized the travel efficiency of the road network.The genetic algorithm was proposed to solve the process. Taking a regional traffic network in Nanjing as an example, the results show that the optimized network performance is better than that of the original road network. Both the speed of the road network running and the service level are improved.Both maintenance costs and delays are reduced. The bi-level programming model is mainly used to reform and upgrade the road sections with the low level and the high saturation in the road network. In a certain cost range,realizing the optimal balance between traffic congestion and costs can provide a reference for road network optimization decisions.

traffic congestion; road network optimization; bi-level programming;genetic algorithm

10.3969/j.issn.1001-0505.2017.03.031

2016-09-03. 作者简介: 诸云(1985—),女,博士生;王建宇(联系人),男,博士，教授,博士生导师,jianyu_wang2000@163.com.

国家自然科学基金资助项目(51178157)、国家统计科研计划资助项目(2012LY150)、中央高校基本科研业务费专项资金资助项目(30916011338)、江苏省普通高校专业学位研究生创新计划资助项目(SJLX16_0154).

诸云，王建宇，高宁波，等.基于拥堵辨识的城市路网优化模型[J].东南大学学报(自然科学版),2017,47(3):607-612.

10.3969/j.issn.1001-0505.2017.03.031.

U294

A

1001-0505(2017)03-0607-06