折线模糊数的重心定位及其排序方法

王 钦，李贵春

(天津师范大学管理学院，天津 300387)

折线模糊数的重心定位及其排序方法

王 钦，李贵春

(天津师范大学管理学院，天津 300387)

给出了折线模糊数的定义及其有序表示，并结合两个具体例子讨论了折线模糊数与其有序表示的对应关系.提出了折线模糊数的重心定位计算公式及其指标排序准则，并通过实例验证了折线模糊数排序方法的有效性.

模糊数;折线模糊数;有序表示;重心坐标;指标排序

0 引言

在决策分析和优化问题中模糊数的排序占有十分重要的地位，但由于基于Zadeh扩展原理的模糊数算术运算不满足封闭性，从而导致模糊数运算极其复杂和繁琐.2002年，刘普寅[1]首次提出折线模糊数概念，并通过n-折线模糊数的扩展运算来近似替代传统的Zadeh扩展运算，进而研究了折线模糊神经网络的泛逼近性.文献[2]系统地给出了折线模糊数的算术运算法则及其相关性质.文献[3]从数学理论层面讨论了折线模糊数空间的完备性.此外，由于折线模糊数可用有限个有序实数表示，故在处理模糊信息时具有一定优势.例如，折线模糊神经网络可将内部运算直接作用在特殊模糊集上，并通过折线模糊数的有限个点来进行信息处理.2012年，文献[4]通过引入等距剖分方法对折线模糊数定义做了改进，并在K-积分模意义下研究了折线模糊神经网络对一类可积函数的逼近性.文献[5]基于折线模糊数的扩展运算构造了一个具体的三层前向折线模糊神经网络模型.然而，上述这些方法和结果始终回避一个关键问题，那就是折线模糊数该如何排序?

事实上，模糊数的排序是讨论多属性决策分析和优化问题的一个关键性指标，以往人们从不同角度对三角形模糊数或梯形模糊数给出若干排序准则和排序方法.[6-9]然而，这些方法在不同程度上都存在丢失信息的现象，迄今为止，对一般模糊数的排序方法罕见于已有文献.这不仅是因为一般模糊数的结构和算术运算复杂多样，而且是因为模糊数自身结构缺乏一个统一的指标准则.本文将通过引入折线模糊数作为衡量模糊数的指标排序准则，并系统讨论了折线模糊数与其有序表示的对应关系，进而基于重心定位坐标提出折线模糊数的指标排序准则及其排序方法.

1 折线模糊数

由于一般模糊数不能简单地进行线性运算，且只能依赖于颇为复杂的Zadeh扩展原理进行算术运算，这给模糊数的应用带来了许多不便.为克服这些不足，文献[1]率先引入折线模糊数概念.

本文一律用Rn表示n维欧式空间，N表示自然数集，R+表示正实数集，F0(R)表示R上全体普通模糊数构成的集合.

图1 n-折线模糊数的隶属函数图像

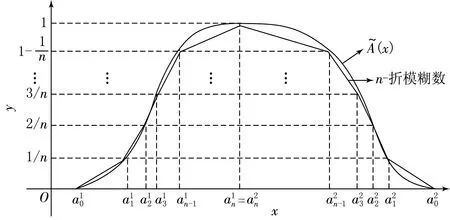
图2 模糊数与等距分片后n-折线模糊数的隶属函数图像

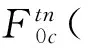
事实上，引入折线模糊数的重要意义远不止于此，重要的是其对每个普通模糊数都可依据不同n值截取一个n-折线模糊数，换言之，一般模糊数可用n-折线模糊数来逼近或近似表示，见图2.

依图2不难看出，对给定模糊数来说，其对应折线模糊数主要依赖于n值的选取.n值越大所得分片和结点越多，该折线模糊数逼近所给模糊数的能力就越强，但其复杂程度也随之加大.

2 折线模糊数的有序表示

事实上，若给定一个折线模糊数的解析表达式，不仅n值可确定，而且其有序表示也可确定.反之，若给定2n+2个有序实数(有序表示)，也可唯一确定折线模糊数的解析表达式.下面将通过实例来进一步讨论折线模糊数与其有序表示的对应关系.

图3 有序表示所对应的3-折线模糊数的隶属函数图像

此外，由于所给有序表示中含有8个有序实数，故令2n+2=8，解之n=3.这意味着在y轴的闭区间[0，1]上插入两个分点λ1=1/3，λ2=2/3.此时，待求3-折线模糊数的隶属函数与水平直线y=1/3和y=2/3的交点(结点)坐标为(-4，0)，(-3，1/3)，(0，2/3)，(1，1)，(2，1)，(4，2/3)，(5，1/3)，(7，0).

在平面坐标系内确定上述8个坐标点的位置，然后用直线段依次连接相邻结点，即可获得所求3-折线模糊数的隶属函数图像，见图3.

上述两个实例说明了一个n-折线模糊数与其有序表示是一一对应的关系.

3 重心定位

由于折线模糊数是由若干小梯形叠加而成，且每个小梯形除了自身高度相同外其余部分均有所不同，参见图1—3.实际上，文献[8-9]虽然给出每个梯形模糊数的中心坐标确定方法，但该方法具有一定局限性，况且若将图1中所有小梯形叠加后其重心坐标该如何确定又是一个新问题.

(1)

(2)

4 排序准则

通常情况下重心坐标在三角形或梯形模糊数的排序中扮演着重要角色，但这些方法都具有一定的局限性和不同程度缺陷.例如，Cheng[6]提出三角形模糊数排序指标公式，但该公式对重心相同的三角模糊数却无法排序;Chu等[7]虽提出改进的排序指标公式，并且克服了Cheng的缺陷，但它又导致横向和纵向重心坐标乘积相等的三角模糊数无法排序;文献[8]综合采用Cheng和Chu的平均值给出新的排序指标公式，但仍有时陷入Chu的缺陷;文献[10]通过引入平均模糊集概念重新提出了指标排序公式，该公式虽然基本克服了上述缺陷，但涉及复杂的定积分计算，严重影响了排序的效率.实际上，通常人们只是注重对排序指标公式的改进，而忽略对重心坐标的修改，本节将在上述提出重心定位公式(1)—(2)的基础上，依据文献[9]的排序指标给出折线模糊数的排序公式.

(3)

显然，序关系“>”满足传递性、独立性和完全性，故该排序指标准则对于多个折线模糊数排序仍然适用，这些结果可从后边的实例中明显看出.

需要进一步说明的是，上述排序准则仅限折线模糊数的有序表示在同一个n值情况下使用.否则，若所取n值不同，会导致重心坐标乃至所有指标都发生改变.事实上，待将来进一步研究模糊数的排序问题时，固然都是选取同一个n值来进行等距分片.

5 实例分析

下面通过给定一组折线模糊数的有序表示，按照上述排序指标公式和排序准则来进行具体排序.这里为简便起见，不妨选取n值为3.

按照定义1及其有序表示，不难将这4个3-折线模糊数放置图4中.

图4 例3中4个3-折线模糊数的隶属函数图像

现按公式(1)—(2)计算横向重心坐标和纵向重心坐标分别为：

同理，也可计算出其他横向和纵向重心坐标分别为：

将此重心坐标代入排序指标公式(3)得

从例1中不难看出，若给定一组折线模糊数的有序表示(限定固定n值)，可先依公式(1)—(2)分别计算每个有序表示的横向和纵向重心坐标，进而按照公式(3)即可获得排序指标K(·)的确切值.

6 结论

折线模糊数是一个比较新的概念，它的提出起源于一般模糊数的算术运算.正因如此，折线模糊数的一些优良性质自然还要回归于模糊数的应用.本文首次针对折线模糊数提出有序表示、横向重心坐标和纵向重心坐标等重要概念，并给出重心平均排序指标和指标排序准则步骤.最后，通过实例给出一组3-折线模糊数的排序方法.事实上，任何一个普通模糊数都可用一组折线模糊数来逼近或近似表示，因此折线模糊数排序的意义远不在于其自身，更重要的是它为一般模糊数的排序搭建了一个桥梁!当然，对一般模糊数的排序也是下一步将要重点探讨的问题.

[1] 刘普寅.一种新的模糊神经网络及其逼近性能[J].中国科学(E辑)，2002，32(1):76-86.

[2] LIU P Y，LI H X.Symmetric polygonal fuzzy number space [J].Journal of Fuzzy Mathematics，2007，15(1):27-42.

[4] 王贵君，李晓萍.K-积分模意义下折线模糊神经网络的泛逼近性[J].中国科学(信息科学)，2012，42(3):362-378.

[5] 李丹，孙刚，王贵君.一类三层前向折线模糊神经网络的构造[J].东北师大学报(自然科学版)，2012，44(3):55-59.

[6] CHENG C H.A new approach for ranking fuzzy numbers by distance method [J].Fuzzy Sets and Systems，1998，95：307-317.

[7] CHU T C，TSAO C T.Ranking fuzzy numbers with an area between the centroid points and original point [J].Computers and Mathematics with Applications，2002，43：111-117.

[8] WANG Y M，YANY J B，XU D L，et al.On the centroids of fuzzy numbers [J].Fuzzy Sets and Systems，2006，157：919-926.

[9] 赵娟，刘琼荪.一种基于模糊数中心的模糊数排序方法[J].模糊系统与数学，2008，22(2):142-146.

[10] 王秀荣，张俊容.一种新的模糊数排序方法[J].统计与决策，2012，8：78-80.

[11] 王涛，李键，李井翠.模糊数的一种梯形模糊数的逼近方法[J].统计与决策，2010，17：31-33.

[12] 钱存华，张琳，戴槟，等.三角模糊数的加权平均及其在评价决策中的应用[J].运筹与管理，2005，14(2):5-9.

(责任编辑：李亚军)

Centroid positioning of the polygonal fuzzy number and its ordering method

WANG Qin，LI Gui-chun

(School of Management，Tianjin Normal University，Tianjin 300387，China)

The definition of polygonal fuzzy number and its ordered expression are given and the corresponding relationship between polygonal fuzzy number and its ordered expression is discussed through two specific examples.The calculation formulas of the centroid positioning of polygonal fuzzy number and the criterion of the index ranking are put forward.The effectiveness of the ordering method of polygonal fuzzy numbers is verified through a practical example.

fuzzy number；polygonal fuzzy number；ordered expression；centroid coordinates；index ranking

1000-1832(2017)02-0025-05

10.16163/j.cnki.22-1123/n.2017.02.006

2016-01-11

国家自然科学基金资助项目(61374009).

王钦(1989—)，男，硕士，主要从事物流管理与决策分析研究；通信作者：李贵春(1964—)，男，博士，教授，主要从事物流管理、决策分析与供应链研究.

O 159 [学科代码] 110·74

A