定子无铁心轴向磁场永磁电机永磁体涡流损耗研究

刘福贵，杨乾坤，王彦刚

(河北工业大学，天津300130)

0 引 言

定子无铁心轴向磁场永磁电机(以下简称AFPM)不同于传统电机具有的硅钢片和槽式绕组结构，定子无铁心结构消除了传统电机中的磁滞损耗和涡流损耗，无刷、无磁阻尼和无齿槽结构避免了齿槽效应带来的转矩波动;而这种电机又具有结构紧凑、轴向尺寸短、功率密度高和运行性能好等优点，被广泛应用于电动汽车、数控机床、船舶推进系统等领域。由于其特殊的结构和复杂的磁场，在高速运行过程中必然会存在大量谐波，使永磁体磁场发生畸变，降低电机效率和性能，也可以使永磁体温度严重升高甚至出现退磁或转子烧毁现象。因此，通过对无铁心AFPM永磁体涡流损耗进行建模计算，分析涡流损耗的影响因素，提出抑制或减小永磁体涡流损耗的方法显得尤为重要［1］。

无铁心AFPM作为新型电机，相较于有铁心有槽的轴向磁场电机以及永磁电机来说，对其转子涡流损耗计算的文献甚少，但由于无铁心AFPM与这两种电机在结构上具有一定的相似性，众多学者通过这种电机的相关文献来研究无铁心AFPM的转子涡流损耗。文献［2］推导了计算无铁心AFPM转子涡流损耗的解析公式。文献［3］研究了内嵌式永磁同步电动机永磁体在不同电流谐波分量影响下产生的涡流损耗。文献［4］分析了3种永磁体分块方法，理论分析永磁体分块在转子涡流损耗减小方面有显著效果，但未分析怎样分割对涡流损耗减小更显著。文献［5］提出一种将永磁体不完全分块的方法来减小转子涡流损耗。文献［6］对盘式定子无铁心永磁电机转子涡流损耗进行了研究，并论证其分块方法，但未就具体分块数对涡流损耗密度及涡流损耗进行计算分析。

本文以一台11 kW、内定子、双转子结构的无铁心AFPM为例，利用MAXWELL三维电磁场有限元分析软件建立电机有限元模型，在三相正弦电流源驱动下求解电机永磁体电磁场分布，为减小永磁体涡流损耗，对永磁体进行不同方向分割，并对不同方向分割进行仿真对比。为近一步减小涡流损耗，结合变压器工程应用上的TEAM Problem 21基准族中的相关知识，利用电磁屏蔽原理减少永磁体涡流损耗，并利用MATLAB曲线拟合得出屏蔽层厚度的最优值，这对电机安全、稳定、高效运行意义重大。

1 无铁心AFPM损耗

无铁心AFPM损耗主要包括定子损耗、转子损耗及机械损耗［7］。

1． 1 定子损耗

有国内外学者针对无铁心轴向磁场电机绕组涡流损耗计算方面进行了研究［8－9］，有的学者提出利用利兹线来绕制电枢绕组，有的学者提出使用扁铜线或者减小导线的厚度来减小损耗［10］。虽然使用利兹线可以在一定程度上减小绕组涡流损耗，但是利兹线较高的造价却使其不能广泛地使用，加之并联绕组间可能出现反电动势不完全平衡，产生环流造成损耗，而且较软的利兹线在绕制浇注绕组时会产生一定的困难;定子损耗除了绕组涡流损耗外还有绕组电阻产生的铜耗，可以通过解析式获得。

1． 2 转子损耗

电机内部会产生两种磁通变化:一种是磁通和时间函数，是时变电流产生的;另一种是磁通和空间函数，是转子旋转时永磁体与磁场发生相对运动产生的。由于钕铁硼有较高的电导率，会随着磁通的变化而产生涡流，其转子涡流损耗解析式:

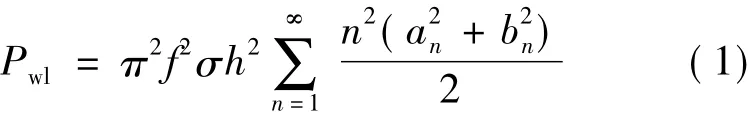
式中:h表示永磁体磁化方向长度;σ表示绕组电导率;n表示电枢电流谐波次数;an和bn表示各次谐波分量在导体内产生的动态磁密幅值。

2 电机电磁场模型建立与仿真

2． 1无铁心AFPM有限元模型建立

本文研究的无铁心AFPM结构如图1所示，具有高度对称性，故建立1/4电机模型，其绕组为两串四并星形连接，如图2所示，无铁心AFPM几何模型如图3所示，表1为主要参数。

图1 AFPM结构图

图2 绕组排列

图3 几何模型

表1 无铁心AFPM主要参数

2． 2无铁心AFPM有限元仿真

在完成三维几何模型建立和边界条件设置后，接下来对模型中各部分附加材料属性、激励源等设置。特别说明的是，模型两侧的永磁体充磁方向为轴向平行充磁，如图4所示。由于需要考虑集肤效应，所以需要在集肤效应层进行加密剖分，而集肤效应层之下的网格则可以相对较为稀疏。为得到更好的剖分网格，可以适当加密剖分层数，图5为求解域设置及网格剖分后的模型。

图4 轴向平行充磁

图5 网格剖分图

2． 3无铁心AFPM有限元仿真结果及分析

2．3．1无铁心AFPM空载下磁感应强度仿真结果分析

当对绕组施加零电流激励，并给电机设定恒定转速运行时，可以得到空载下电机的瞬态磁场分布情况，如图6所示。

由图6可以看出，无铁心AFPM转子磁轭的磁密值最大，永磁体次之，气隙磁密值最小。转子永磁体端部处的磁密差异较小，这是由于边缘效应引起的，在转子内外半径处，磁密幅值逐渐减小，且内半径处磁密减小幅度较外半径减小幅度稍大，空载时无铁心AFPM最高磁密达到了1．917 7 T。

图6 空载瞬态磁场分布

2．3．2无铁心AFPM负载下磁感应强度仿真结果分析

当绕组通入正弦波激励源时，便得到电机负载下的瞬态磁场分布，如图7所示。

图7 负载瞬态磁场分布

由图7可以看出，无铁心AFPM转子各部位磁密值分布与图6大体上相似，但是通入负载后的平均磁感应强度略小于空载时的平均磁感应强度，通过分析，这是由于电枢绕组在通入激励后产生电枢反应导致的，电枢反应会削弱永磁体产生的磁场。

2．3．3负载下转子涡流损耗仿真结果分析

在正弦波驱动下，平均输出转矩为145 N·m，转速为750 r/min时，无铁心AFPM永磁体涡流损耗随时间变化的计算结果如图8所示。

从图8中可以看出，转子永磁体平均涡流损耗是206．85 W，对于无铁心AFPM来讲是不可忽视的，通过分析式(1)，下文主要研究永磁体分块对涡流损耗的影响以及分块后又添加屏蔽层对涡流损耗的影响。

2． 4永磁体分块对涡流损耗的影响

永磁体分块降低永磁体涡流损耗的机理:将一块整体永磁体平均分割成多块，每块之间是绝缘层(为了不影响电机的气隙磁密，绝缘层要越窄越好)，其阻断了原来的涡流路径。涡流损耗随着绝缘层数的增加而减少，但是由于制作工艺及永磁体有效尺寸及永磁材料利用率等因素的存在，永磁体分块数不能无限增大，设计时应根据具体要求及实际情况综合考虑。

2．4．1永磁体横向分块对涡流损耗的影响

在保持平均输出转矩为145 N·m与转速为750 r/min不变的情况下，无铁心AFPM永磁体涡流损耗密度分布情况随永磁体横向分割数目增加而变化的仿真计算结果，如图9所示。

图9 横向分割涡流损耗密度分布情况

无铁心AFPM在上述恒定转矩及转速下，用有限元计算所得到的永磁体涡流损耗随分割块数增加的损耗值变化曲线如图10所示。

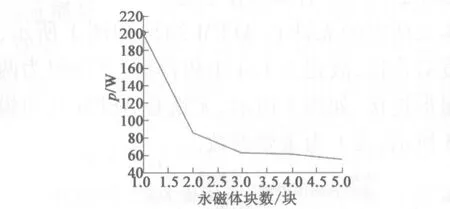
图10 永磁体横向分成不同块数的涡流损耗变化曲线

通过图10可以直观看出，使用永磁体分块的方法对永磁体涡流损耗减小方面有显著效果，分为两块较一整块时减小效果最为明显，分为4块虽比分为3块有所减小，但是效果已没有3块较两块时那么显著，考虑到制作工艺及永磁体有效尺寸变化及永磁材料利用率等因素的存在，永磁体横向分割为3块最为合适。

2．4．2永磁体竖向分块对涡流损耗的影响

同样，在保持平均输出转矩为145 N·m与转速为750 r/min不变的情况下对无铁心AFPM永磁体进行竖向分割，为了与横向分割进行对比，本文只分析竖向分割为3块和4块两种类型。涡流损耗密度分布仿真结果如图11所示，对应的涡流损耗变化曲线如图12所示。

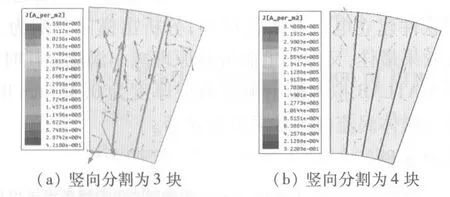
图11 竖向分割涡流损耗密度分布情况

图12 竖向分割涡流损耗变化曲线

通过图12可以看出，竖向分割为3块时的平均涡流损耗为127．95 W，竖向分割为4块时的平均涡流损耗为61．04 W。

综上，对比其分割方向可知，使用横向分割对永磁体涡流损耗减小效果更佳。

2． 5屏蔽层对涡流损耗的影响

结合变压器工程应用上TEAM Problem 21基准族中的相关知识，利用电磁屏蔽原理于本课题中以减小永磁体涡流损耗。

在永磁体外部加一层与永磁体形状相似的薄铜片作为屏蔽层来减小永磁体的涡流损耗。当气隙谐波分量进入导电率高的铜层后，在其中产生涡流，由于涡流的反作用使进入永磁体的气隙谐波分量减少，从而减小了永磁体的涡流损耗，且铜的热传导率高，利于热量的散失。

2．5．1屏蔽层单独作用于永磁体

为了证实铜屏蔽层对永磁体涡流损耗减小真实有效，下面对未经分块的永磁体进行有限元仿真验证，如图13所示。

图13 未分块的永磁体涡流损耗密度分布对比

与未加屏蔽层时对比，永磁体涡流损耗密度明显减小，分布也均匀许多;反观铜屏蔽层上的涡流损耗值非常大，如图14所示，准确地验证了屏蔽层能有效地屏蔽气隙谐波分量进入永磁体，使永磁体涡流损耗减小。

图14 铜屏蔽层涡流损耗密度分布

2．5．2分块和屏蔽层同时作用于永磁体

由于已用有限元计算的方式验证了永磁体分块和加入屏蔽层能有效降低无铁心AFPM转子永磁体涡流损耗，本文做出分块和屏蔽层两种方法同时作用于永磁体上时，可以更大幅度减小永磁体的涡流损耗密度这样的设想，下面对这个设想进行有限元电磁场数值计算。以整个永磁体分3块为例，加上铜屏蔽层，仿真出永磁体涡流损耗密度分布(图15)和涡流损耗值变化曲线(图16)。

图15 加屏蔽层永磁体涡流损耗密度分布对比

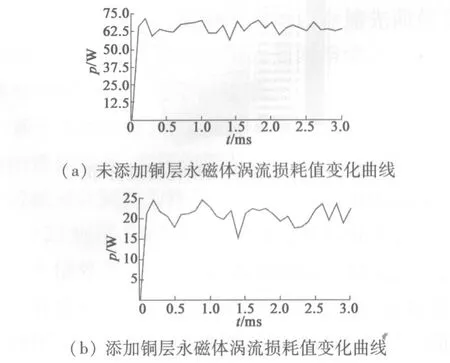
图16 分3块的涡流损耗值变化曲线对比

对比图9(b)与图15，分块和加屏蔽层两种方法同时作用于永磁体上时，可以更大幅度减小永磁体的涡流损耗密度分布。通过图16(a)可以看出，分三块未添加铜屏蔽层永磁体涡流损耗平均值为63．89 W;由图16(b)可知，添加铜屏蔽层后永磁体涡流损耗平均值为20．51 W，从而得出分块和加屏蔽层同时作用于永磁体可以有效减小涡流损耗，论证了上面的设想。

2．5．3屏蔽层厚度最优设计方案

为了使涡流损耗更小，屏蔽层的厚度hc需要有一个最优值;根据电磁波理论，一般情况下以电磁波的波长作为屏蔽层的厚度，即:

式中:λ表示电磁波波长;δ表示透入深度。这样，电磁场不能透过屏蔽体，从而对屏蔽装置内外均起到隔离作用。但是由于电机各个部件实际尺寸及规格的影响，按照电磁波理论完全屏蔽谐波对永磁体的影响是不现实的。下面以屏蔽层厚度对涡流损耗影响用MATLAB曲线拟合得出最优方案。

图17 屏蔽层厚度对涡流损耗影响

拟合得出厚度约0．45 mm时对涡流损耗减小的效果最佳。用MAXWELL软件对屏蔽层厚度为0．45 mm时有限元电磁场数值计算，得出永磁体涡流损耗密度分布，如图18所示，并得出涡流损耗值变化曲线，如图19所示。

通过MAXWELL电磁场有限元分析计算，屏蔽层厚度为0．45 mm时确实对永磁体涡流损耗减小效果最好，其永磁体涡流损耗平均值为17．31 W。

图18 永磁体涡流损耗密度分布

图19 永磁体涡流损耗值变化曲线

3 结 语

定子无铁心AFPM电感小、电流谐波大，永磁体涡流损耗产生的温升可能会使钕铁硼发生不可逆退磁。对这一问题以一台额定功率为11 kW的电机为研究对象，利用MAXWELL三维电磁场有限元分析软件建立电机有限元模型，分析出横向分割为3块效果最佳，又利用电磁屏蔽原理减小涡流损耗时，用MATLAB拟合得出铜屏蔽层厚度为0．45 mm时对永磁体涡流减小效果最为显著。

［1］ 徐永向，胡建辉，邹继斌．表贴式永磁同步电机转子涡流损耗解析计算［J］．电机与控制学报，2009，13(1):63 －66．

［2］ 李娟．永磁体涡流损耗的有限元分析及其对电机性能的影响研究［D］．天津:天津大学，2005．

［3］ 李虎，蒋晓华，毕大强，等．永磁同步电动机中永磁体的三维涡流分析［J］．清华大学学报，2009，49(8):1085 －1088．

［4］ CAVAGNINO A，MIOTTO A，TENCONI A，et al．Eddy currrent losses reduction in fractional slot concentrated winding PM generators for More Electric Engine application［C］//2011 International Conference on Clean Electrical Power(ICCEP)，2011:357 －363．

［5］ WILL D A，KAMPER M J．Reducing PM eddy current rotor losses by partial magnet and rotor yoke segmentation［C］//2010 XIX International Conference on Electrical Machines(ICEM)，2010:1 －6．

［6］ 王晓远．盘式永磁同步电机永磁体内涡流的有限元分析［J］．微电机，2007，40(1):5 －9．

［7］ 阳娜，张牧，郭宝忠，等．定子无铁心轴向磁场永磁电机温度场分析［J］．仿真应用研究，2015，32(1):259－264．

［8］ WANG R J，KAMPER M J．Calculation of Eddy Current Loss in Axial Permanent Magnet Machine with an Coreless Stator［J］．IEEE Transctions on Energy Conversion，2004，19(3):532 －538．

［9］ 汤平华，漆亚梅，黄国辉，等．定子无铁心飞轮电机绕组涡流损耗分析［J］．电工技术学报，2010，25(3):27 －31．

［10］ 邵非非，陈钢．水下航行器用无铁心永磁无刷直流盘式电动机电枢绕组涡流分析研究［D］．西安:中国舰船研究院，2012．