能量回馈型超声波电机的实验研究

高帅帅，王光庆

(浙江工商大学，杭州310018)

0 引 言

超声波电机是一种基于振动和摩擦驱动的微型特种电机，具有低速大扭矩、结构紧凑和快速响应能力等优点，广泛应用于微机构和微型机器人的驱动组件中。主流的行波型超声波电机是由压电定子和转子组成，定子环上表面开有若干齿槽，对定子弹性振动进行放大，提高其输出性能［1－2］。国内外诸多专家学者对此电机进行了结构优化设计、数学模型、控制策略等方面的研究，取得了丰富的研究成果［3－9］。

从功能应用上讲，超声波电机目前主要是提供输出力或力矩，对被控对象(如机器人)进行驱动和定位。而在一些极端环境(如封闭的有毒有害容器、高低温等)中工作的微型机器人，不仅要求电机具有驱动定位功能，其供电也是一个不容忽视的问题。电池供电主要的问题是寿命受限，一旦电池耗电完毕，要进行更换非常困难甚至不太可能，这将导致微机器人失效或停止工作。针对这种极端环境中工作的微型机器人，本文研制了一种能量回馈型超声波电机，电机不仅具有精密驱动和定位功能，还可采集电机在运行过程中的定子振动能量，并将其转换成电能为微电子器件供电。

文献［9］首次对超声波电机定子振动能量回收转换特性进行了理论与实验研究，利用铁摩辛柯梁理论和压电本构方程，建立了电机定子振动能量采集模型，实验研究了定子振动能量采集输出特性。但该模型将复杂定子结构等效成等截面横梁，建立其平面坐标下的采集模型，且实验研究不够全面，本文在文献［9］的基础上，对电机性能进行了综合测试、分析与研究，包括阻抗特性、机械特性、瞬态特性和能量采集输出特性等。研究结果表明，研制的能量回馈型超声波电机达到了设计指标要求，具备驱动与能量采集双重功能。

1 电机设计思路及其设计技术指标

主流行波型超声波电机定子压电陶瓷环的极化模式如图1(a)所示，包括激励区(A，B区)和孤极两部分，其中有3λ/4的压电陶瓷未被极化，如图1(a)阴影部分，这部分陶瓷不仅不参与机电能量的转换，在电机定子高频振动过程中还存在着能量的损耗。

图1 行波型超声波电机压电陶瓷环的极化模式

本文研制的能量回馈型超声波电机，其结构与主流行波型超声波电机结构相似，由环形定子和柔性转子组成，主要区别在于环形定子压电陶瓷极化分区模式与图1(a)模式不同。如图1(b)所示，压电陶瓷极化分区成激励区(A，B区)、孤极和能量采集区，将图1(a)中未被极化部分的压电陶瓷极化后作为能量采集区。当电机稳定运行时，利用压电陶瓷的正压电效应，定子弯曲变形产生的高频机械振动能量被能量采集区压电陶瓷采集并转化为交变的电能(如电压、电流)，经过AC/DC电子电路转变成直流电，实现对微机器人/微电子设备供电。相比于常规的行波型超声波电机，能量回馈型超声波电机具有驱动和能量采集两种功能于一体，能量利用效率更高，适用范围也更加广泛。

研制的能量回馈型超声波电机技术指标要求:

1)电机定子直径为60 mm;

2)空载转速不低于90 r/min;

3)堵转力矩不低于0．6 N·m;

4)能量采集输出功率不低于60 mW;

5)直流供电电压不高于15 V;

6)起动响应时间小于20 ms;

7)停止响应时间小于15 ms。

2 电机样机及实验研究

目前超声波电机实验研究还不够全面，通常仅仅考虑电机能量采集输出特性，没有对电机机械特性、阻抗特性、瞬态特性，特别是能量采集电路负载对电机机械性能的影响等开展实验研究。本文对上述特性开展了详细的实验研究，为电机驱动电路匹配提供设计思路，并且对能量回馈型超声波电机的进一步优化起到关键作用。研制的能量回馈型超声波电机样机如图2所示，电机定子直径60 mm，总重量325 g，其中定子重量150 g。

图2 能量回馈型超声波电机样机

2． 1阻抗特性实验

阻抗特性实验是获取电机定子机电等效参数的重要手段之一。本实验利用超声阻抗分析仪PV70A对能量回馈型超声波电机的阻抗特性进行测试，结果如图3、图4所示。由图4可知，电机的谐振频率为38 740 kHz(预压力为0情况下测得)，静态电容为6．997 nF。由图3、图4的实验结果，还可以识别出电机定子主要机电等效参数，如表1所示，这些参数为超声波电动机的优化设计及电机驱动电路匹配提供设计思路。

图3 电纳和电导组成的导纳圆

图4 阻抗、相位和频率的关系

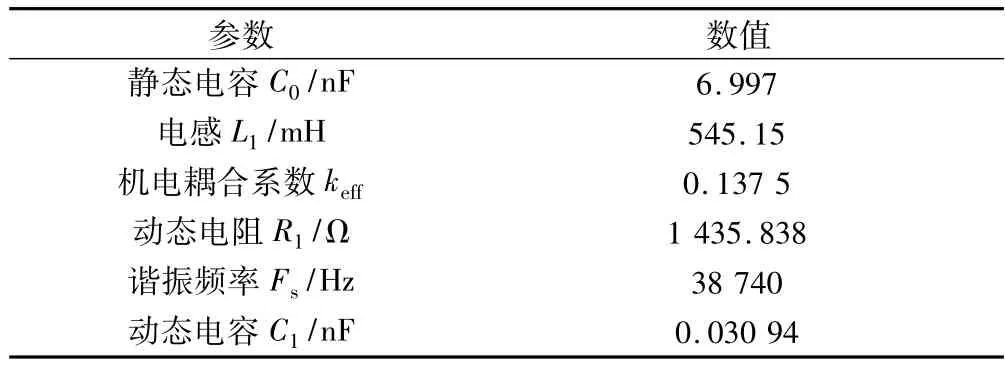
表1 电机定子主要参数测试结果

2． 2机械特性实验

图5 机械特性实验系统

能量回馈型超声波电机机械特性实验系统如图5所示。信号发生器(图中未显示)和功率放大器为超声波电机提供输入激励电压，直流电源为整个实验测试系统提供输入电能，调节直流电源输出电压的大小，可改变功率放大器的输出功率和超声波电机输入激励电压的幅值，从而改变电机的转速。磁滞测功机用来模拟电机负载扭矩，测功机控制器可调节输入测功机的电流，从而改变负载扭矩的大小，同时测量电机转速、功率和力矩并显示。示波器用于监测电机输入电压波形，并测量电机输入电压幅值和频率。

为了考察能量采集区外接负载对电机机械输出特性的影响，将能量采集区压电陶瓷两端接等效负载电阻R。图6和图7分别是激励电压73 V和激励频率40 kHz条件下，电机速度－力矩特性和输出功率－力矩特性随能量采集区负载电阻的变化实验结果。由图6和图7可知，负载电阻R不变的情况下随着输出力矩的增大，电机转速跟着下降，电机机械输出功率先增大后减小。空载时最大转速为118 r/min，堵转时电机力矩最大达到0．67 N·m，最大机械输出功率为2．6 W。由图6和图7还可知，在输出力矩为轻载(输出力矩小于0．3 N·m)时，负载电阻R对电机输出转速和机械输出功率的影响不大;在重载时(输出力矩大于0．3 N·m)，增大负载电阻R，电机的输出速度和机械输出功率增大，直到负载电阻R大于能量采集区压电陶瓷的最佳匹配电阻9．4 kΩ时，电机输出特性保持恒定，如图6和图7中R=11．6 kΩ，22 kΩ 和 47 kΩ 时的输出曲线。

图6 不同电阻下的力矩－速度特性

图7 不同电阻下的力矩－输出功率特性

图8 和图9分别是激励电压73 V，负载电阻6.9 kΩ条件下，电机速度－力矩特性和输出功率－力矩特性曲线随激励频率的变化实验结果。由图8可知，在能量采集区等效负载电阻R不变的情况下，同一激励频率下，电机转速随着输出力矩的增大逐渐减小。输出转速和输出力矩随激励频率的增大逐渐减小，在激励频率为40 kHz时，电机空载转速达到最大118 r/min，输出力矩最大达到0．67 N·m;在激励频率为42 kHz时，电机空载转速减小到20 r/min，输出力矩减小到0．4 N·m。由图9可知，随着输出力矩的增大，输出功率先增大后减小且有一个最大值。随着激励频率的增大，电机机械输出功率逐渐减小。在激励频率为40 kHz时，最大机械输出功率为2．6 W;激励频率为42 kHz时，最大输出功率降为0．1 W。

图8 电机转速－力矩特性随频率变化结果

图9 电机输出功率－力矩特性随频率变化结果

2． 3振动能量采集特性实验

电机定子振动能量采集输出特性实验系统如图10所示。驱动控制器为超声波电机提供输入激励电压，直流电源为整个实验测试系统提供输入电能，调节直流电源输出电压的大小，可改变功率放大器的输出功率和超声波电机输入激励电压的幅值，从而改变电机的转速。能量采集区采集的输出电压由示波器采集、记录和显示［12］。

图10 定子振动能量采集特性实验系统

图11 、图12和图13分别是激励频率39．4 kHz、激励电压67 V时能量采集区输出电压、输出电流和输出功率随负载电阻R变化的实验结果。由图11可以看出，随着负载电阻R的增大，采集区输出电压U逐渐增大，达到极值70 V后保持恒定。这是由于负载电阻R与能量采集区压电陶瓷的阻抗Z=1/(j2πfCp)组成串联电路，当负载电阻R较小时，输出电压在R上的分压也小，随着负载电阻R的增大，采集输出电压在其上的分压也逐渐增大。当负载电阻R远远大于|Z|时，采集输出电压几乎全部由负载电压R承担，负载电路相当于开路状态。由图12可知，流经负载电阻R的最大电流I为7．8 mA，且随着负载电阻R的增大逐渐减小，这是由于负载电阻R增大的速率ΔR大于输出电压增加的速率ΔU，根据ΔI=ΔU/ΔR可知，输出电流将逐渐减小。由图13可知，负载电路R的输出功率P=UI存在一个最大值，当R=9．4 kΩ时，最大输出功率为320 mW。此时，负载电阻R与能量采集区压电陶瓷阻抗完全匹配，这与图6、图7的实验结果相吻合。

图11 采集输出电压随负载电阻的变化结果

图12 采集输出电流随负载电阻的变化结果

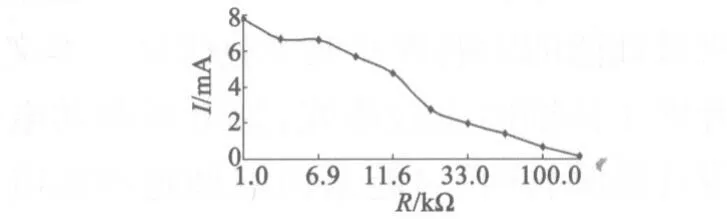
图13 采集输出功率随负载电阻的变化结果

图14 是电机空载时采集输出电压随激励频率的变化实验结果，其中激励电压67 V。由图14可知，不同负载电阻R条件下，能量采集输出电压曲线均在激励频率39．4 kHz处达到最大，这说明空载时能量采集区负载电阻R对电机谐振频率影响很小，这也间接说明了轻载时负载电阻R对电机输出速度、力矩和机械输出功率影响不大，这与图6和图7的实验结果是吻合的。另外，当激励频率一定时，采集输出电压随着负载电阻R(除R=0外)的增大而增大。由于负载电阻R与能量采集区压电陶瓷的阻抗Z=1/(j2πfCp)组成串联电路，当负载电阻R较小时，输出电压在R上的分压也小;随着负载电阻R的增大，采集输出电压在其上的分压也逐渐增大。当负载电阻R|Z|时，如负载电阻R=470 kΩ时，压电陶瓷采集输出电压几乎全部由负载电阻R=470 kΩ分压得到，此时负载电阻相当于开路状态。特别地，负载电阻R=0时，表明能量采集区压电陶瓷输出端处于开路状态，此时，测量得到的输出电压为压电陶瓷输出电压，且与R=470 kΩ时的输出电压曲线接近。

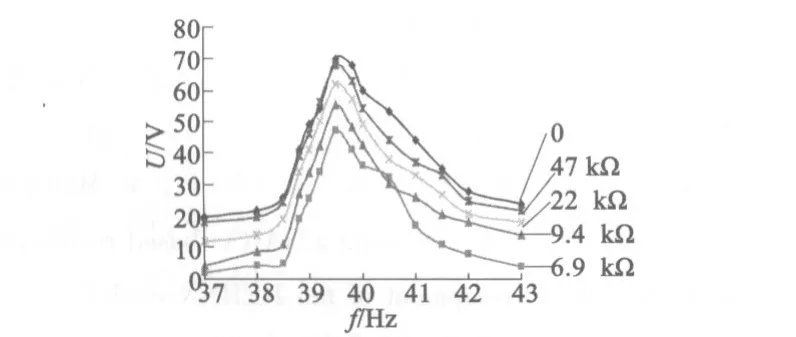
图14 采集输出电压随激励频率的变化结果

2． 4瞬态特性实验

超声波电机的一个重要特点就是响应速度快，响应时间为ms级别，因而它的控制性能较好。响应速度快主要体现在起动和关断过程时间特别短，即从零速度突然起动到稳定速度或从某稳定的速度突然关断到零速度所需的时间特别短。电机能量采集输出电压与定子振动位移(速度)是成正比的。因此，本文通过测试能量采集区输出电压波形来研究电机的起动和关断特性。为了能够捕获电机快响应的起动和关断特性，测试时将示波器的时间分辨率调整为1 ms。图15和图16分别是超声波电机在激励频率40 kHz，无负载条件下的起动和关断时能量采集区输出电压波形图。由图15和图16可知，在电机开启的瞬间电压先是瞬间上升到峰值90 V，然后震荡趋于稳定，经过6 ms左右电机进入稳定运转阶段，此时采集输出电压稳定于70 V。由于定转子接触面间的摩擦制动效应，电机断电后，反馈电压大约持续1．2 ms后减小至零，可见关断时间比起动时间更小，这说明电机具有较快的响应能力。

图15 空载起动特性

图16 空载关断特性

综合实验研究结果，总结能量回馈型超声波电机的主要性能参数，结果如表2所示。

表2 电机性能参数

表2的实验结果表明，所研制的能量回馈型超声波电机达到了电机设计技术指标要求。

3 结 语

本文研制了能量回馈型超声波电机，建立了电机能量采集理论模型，开展了电机实验研究，得到以下结论:

(1)研制的能量回馈型超声波电机达到了设计技术指标要求。阻抗实验表明研制的超声波电机的谐振频率为38 740 Hz(预压力为0情况测得)，静态电容为6．997 nF。阻抗特性实验确定了超声波电动机的模态频率、夹持电容和等效电感等参数，为超声波电动机的优化设计及电机驱动电路匹配提供设计思路。

(2)轻载时，能量采集区外接负载电阻对电机机械输出特性和谐振频率影响不大;重载时，增大负载电阻，电机机械输出性能增大。电机空载转速为118 r/min，堵转力矩为0．67 N·m，最大机械输出功率2．6 W。

(3)电机起动和关断响应速度快，起动时间和关断时间分别为6 ms和1．2 ms。

(4)能量采集区在最佳匹配负载电阻R=9．4 kΩ时，最大输出电压为70 V，最大输出电流7．8 mA，最大输出功率为320 mW。

［1］ ANTONIOI，MASSIMOP．A high － power traveling wave ultrasonic motor［J］．IEEE Transactions on Ultrasonic，Ferroelectrics，and Frequency Control，2007，53(7):1344 －1351．

［2］ BOLBORICI V，DAWSONF P，PAUGH M C．A finite volume method and experimental study of a stator of a piezoelectric traveling wave rotary ultrasonic motor［J］．Ultrasonics，2014，53(3)809 －820．

［3］ 赵淳生．超声波电机技术与应用［M］．北京:科学出版社，2007．

［4］ MASHIMO T．Micro ultrasonic motor using a one cubic millimeter stator［J］．Sensors and Actuators A Physical，2014，213(7):102 －107．

［5］ 王光庆，沈润杰，郭吉丰．压电陶瓷对超声波电动机定子特性的影响［J］．机械工程学报，2010，46(4):8 －14．

［6］ LEROY E，LOZADA J，HAFEZ M．A curved ultrasonic actuator optimized for spherical motors:design and experiments［J］．Ultrasonics，2014，54(6):1610 －1619．

［7］ ZHANG Y H，QU J J，LI J B．Friction and wear behavior of linear standing－wave ultrasonic motors with V －shape transducers［J］．Tribology International，2016，95(11):95 －108．

［8］ MORITA T，NIINOT，ASAMA H．Rotational feed through using ultrasonic motor for high vacuum condition［J］．Vacuum，2002，65(1):85－90．

［9］ 曲建俊，李锦棒．基于电接触法的行波型超声电机接触特性研究［J］．声学学报，2015，40(5):625 －630．

［10］ 王光庆，陆跃明，郭吉丰．超声波电动机定子振动能量回收转换特性［J］．浙江大学学报:工学版，2013，47(1):174 －181．

［11］ UCHIO K．Piezoelectric actuators and ultrasonic motors［M］．Springer Publishing Company，Incorporated，2011．

［12］ LONGINI I M J，ACKERMAN E，KEMPER J．An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations［J］．Smart Materials and Structures，2009，18(2):25009－25018．