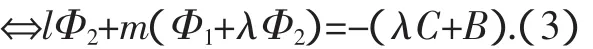谈对一类斜率问题的探究
筅江苏省张家港市沙洲中学戴御梅
谈对一类斜率问题的探究
筅江苏省张家港市沙洲中学戴御梅
在高考和竞赛中,常常出现这类问题:曲线上一定点P引出两动弦PQ、PR,这两弦的斜率之和为定值,则动直线QR恒过定点或kQR恒为定值;平面内与两定点连线斜率之和、差、积、比为定值(不为0)的点的轨迹是什么样的?它们有怎样的性质?下面就这类问题进行探究.
一、与两定点连线斜率之和为定值的点的轨迹及方程
探究1:平面内与两个定点连线斜率之和为定值的点的轨迹.
不妨设两定点为F1(-c,0)、F2(c,0)(c>0),动点与两个定点连线斜率之和为t.
设动点为P(x,y),因为所探究的与两定点连线的斜率都是存在的,所以x≠±c,否则无意义.
故由kPF1+kPF2=t可得
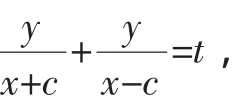
即2xy=tx2-tc2,这就是所求轨迹的方程.
那么它的轨迹是什么?
易知x≠0,将2xy=tx2-tc2变形后可得

①当t>0时,其轨迹为双曲线(不含F1、F2两点),且图像关于原点中心对称,存在两条渐近线,其中一条为y轴.t越接近于0,双曲线越弯曲;t→+∞时,图像趋于两条直线.
②当t<0时,其轨迹还是为双曲线(不含F1、F2两点),且图像关于原点中心对称,存在两条渐近线,其中一条为y轴.t越接近于0,双曲线越弯曲;t→-∞时,图像趋于两条直线.
二、与两定点连线斜率之差为定值的点的轨迹及方程
探究2:平面内与两个定点连线斜率之差为定值的点的轨迹.
不妨设两定点为F1(-c,0)、F2(c,0)(c>0),动点与两个定点连线斜率之差为t.
设动点为P(x,y),因为所探究的与两定点连线的斜率都是存在的,所以x≠±c,否则无意义.
故由kPF1-kPF2=t可得
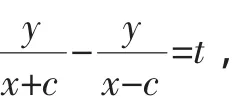

所以,其轨迹为抛物线.(同理可得kPF2-kPF1=t也具有类似的轨迹方程,由于篇幅原因,不再讨论,下同)
①当t>0时,其轨迹为抛物线(不含F1、F2两点),开口向下,且关于y轴对称.t越大,抛物线的开口越小;t→+∞时,图像趋于两条直线,两直线在无穷远处交于点
即-2cy=tx2-tc2,这就是所求轨迹的方程.
那么它的轨迹是什么?
将轨迹方程-2cy=tx2-tc2变形后可得
②当t<0时,其轨迹仍是抛物线(不含F1、F2两点),开口向上,且关于y轴对称.t越小,抛物线的开口越小;t→-∞时,图像趋于两条直线,两直线在无穷远处交于点
三、与两定点连线斜率之积为定值的点的轨迹及方程
探究3:平面内与两个定点连线斜率之积为定值的点的轨迹.
设两定点为F1(-c,0)、F2(c,0)(c>0),与两个定点连线斜率之积为t.
设动点为P(x,y),因为所探究的与两定点连线斜率都是存在的,所以x≠±c,否则无意义.
故由kPF1×kPF2=t可得

即tx2-y2=tc2,这就是所求轨迹的方程.
那么它的轨迹是什么?
将轨迹方程tx2-y2=tc2,变形后可得
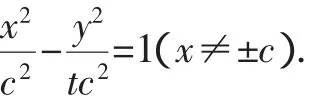
①当t>0时,其轨迹为双曲线(不含F1、F2两点),且关于原点中心对称,存在两条渐近线,其渐近线方程为y= ±x,图像关于x、y轴对称,其离心率为越接近于0,双曲线越弯曲;t→+∞时,图像趋于两条直线.
②当-1 ③当t=-1时,其轨迹方程为x2+y2=c2(不含F1、F2两点).其轨迹为以c为半径且圆心在原点的圆,图像关于原点中心对称,关于x、y轴对称. ④当t<-1时,其轨迹为椭圆(不含F1,F2两点),且关于原点中心对称,关于x、y轴对称.其离心率为,t越小,椭圆越扁,此时焦点在y轴上.t→-∞时,图像越趋于两条直线,两直线 探究4:平面内与两个定点连线斜率之比为定值的点的轨迹. 设两定点为F1(-c,0)、F2(c,0)(c>0),与两个定点连线斜率之比为t. 设动点为P(x,y),因为所探究的与两定点连线斜率都是存在的,所以x≠±c,否则无意义. 由kPF1÷kPF2=t可得 那么它的轨迹是什么? 当t=1时,代入(1-t)x=ct+c,得0=c+c,即c=0,这与假设c>0矛盾,所以t≠1. 当t≠1时,将其变形后可得 所以,其轨迹为一条直线. ①当t>1时,其轨迹为一条在y轴左侧的直线,t越大,越靠近y轴.当t→+∞时,其轨迹趋于x=-c所在的直线. ②当0≤t<1时,其轨迹为一条在y轴右侧的直线,t越小,越靠近y轴.当t→0时,其轨迹趋于x=c所在的直线. ③当t<0时,其轨迹为一条直线,在x=-c和x=c之间移动.t越小,越靠近x=-c所在的直线.当t→-∞时,其轨迹趋于x=-c所在的直线. 探究5:二次曲线Ф:Ax2+Bxy+Cy2+Dx+Ey+F=0上有一定点P(x0,y0)和异于点P的两动点Q、R,则kPQ+kPR= λ≠-且为定值的充要条件是动直线QR过定点的充要条件是,其中Ф1=2Ax0+By0+D,Ф2=Bx0+2Cy0+E. 证明:做平移:x′=x-x0,y′=y-y0,代入Ф(x,y)=0,得 Ax′2+Bx′y′+Cy′2+Φ1x′+Φ2y′=0.(1) 设QR的方程为lx′+my′=1,代入(1),得 Ax′2+Bx′y′+Cy′2+(Φ1x′+Φ2y′)(lx′+my′)=0,整理得是方程(2)的两根, 一般来说,教材中给出知识是最精练的学科知识,不会进行更加深入的探究.这是因为教材作为人类知识的精华,不可能、也不允许对一个问题作长篇幅的阐述.但是,在数学教学中,教师如果只是讲课本上的知识,不对相关问题进行拓展与挖掘,学生就不能养成自我探索与自我反思的思维习惯.数学教学中,教师应该结合课本内容和学生的实际情况,对教材知识进行适当的拓展,设计一些既能够激发学生探究兴趣,又能够让学生经历思考,进行探索的题目,这对学生数学思维能力的提高会有很大的帮助. 因此,在数学教学中,数学教师应有意识地提出一些学生感兴趣的、并有一定深度的课题,组织学生开展讨论,在师生互相切磋、共同研究中来增进师生、同学之间的情谊,培养积极的情感.我们看到,许多优秀的教师,他们的成功,很大程度上是与学生建立起了一种非常融洽的关系,相互理解,彼此信任,情感相通,配合默契.教学活动中,通过师生、生生、个体与群体的互动,合作学习,真诚沟通.老师的一言一行,甚至一个眼神,一丝微笑,学生都心领神会.而学生的一举一动,甚至面部表情的些许变化,老师也能心明如镜,知之甚深,俗话说“心有灵犀一点通”.没有“灵犀”不易通,有了“灵犀”,才能“一点就通”,这“灵犀”,就是我们的老师在长期的教学活动中,与学生建立起来的相互理解.四、与两定点连线斜率之比为定值的点的轨迹及方程
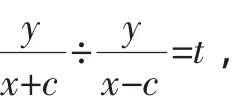

五、定点P引出两动弦PQ、PR,这两弦的斜率之和为定值,则动直线QR恒过定点或kQR恒为定值