非强制环流混合器中的颗粒速度特性

孟振亮，张博峰，刘梦溪，王 维，卢春喜

1.中国石油大学（北京）重质油国家重点实验室，北京102249；2.中国科学院过程工程研究所多相复杂系统国家重点实验室，北京100080

颗粒混合程度对气固流化床反应器中的传质、传热、反应器效率等具有重要影响。相较于传统的流化床，气固环流反应器内存在颗粒的有序环流运动，增强了颗粒流沿径向的流动，显著提高了颗粒在反应器中的混合效率[1,2]。Fang等[1]对比了带有挡板的环流混合器与自由床的颗粒混合效率，发现在相同操作条件下，环流混合器的混合效率提高了约50%。Liu等[2]提出了一种带有预混段与环流反应器耦合的混合器，颗粒在预混段的混合效率高达 70%，而经过环流部分后的最终混合效率为 95%以上。张博峰等[3]在Liu[2]的混合器基础上，将导流筒去掉，保留原有的布气方式，提出了一种结构更加简单的环流混合器（非强制环流混合器），并对其床层浓度以及颗粒混合效果进行了研究。研究发现，在传统环流混合器与非强制环流混合器中冷热颗粒均能够很好地混合，并且在进料影响区，非强制环流混合器的混合效果要优于传统的环流混合器。与传统的环流混合器相比，非强制环流混合器的结构更加简单，却能够实现近似的混合效果。显然，这与非强制环流混合器内的流场密切相关，为了揭示两相流场对颗粒混合的影响规律，有必要对非强制环流混合器中的流场展开研究。

前人的研究[4]表明，气固流化床中颗粒沿轴向的混合较为容易，而沿径向的混合则十分困难，前者的扩散系数比后者高出一个数量级，颗粒的速度场，尤其是沿径向的速度分布是影响颗粒混合的关键因素。由于实验条件的限制，局部区域内颗粒的时空流动与混合难以测量。而随着计算能力的增强，计算流体力学提供了一种有效描述流体动力学的方法。与传统的均匀化曳力模型相比，EMMS（The Energy-Minimization Multi-Scale）模型[5,6]考虑了流化床中气泡、聚团、乳化相之间的作用，因而能够更准确地反映出介尺度流动结构对流动和混合的影响。研究者曾采用EMMS模型对鼓泡床[7,8]以及工

下料管向下流入的颗粒与下部空管区中向上流动的颗粒逆流接触，颗粒再次进行强烈的混合，混合颗粒向上运动进入上部下降管区，颗粒与气体在床层表面分离之后进入边壁区向下运动，在底部区，一部分颗粒沿径向流入中心区进行再次循环，其余颗粒经两个分布器之间的缝隙流出混合器。与传统的环流混合器（如图2(b)所示）相比，颗粒在非强制环流混合器中的流动，不受导流筒的限制。在下部空管区以及上部下降管区中，中心处向上运动的颗粒向外流动进入边壁区，与边壁区的颗粒实现错流混合，同时边壁区向下运动的颗粒，也会沿径向流动进入中心区，实现颗粒的多次循环。此外，去掉导流筒之后，边壁区的气含率增加，将有效改善颗粒在边壁区的流化效果，避免死区的出现。

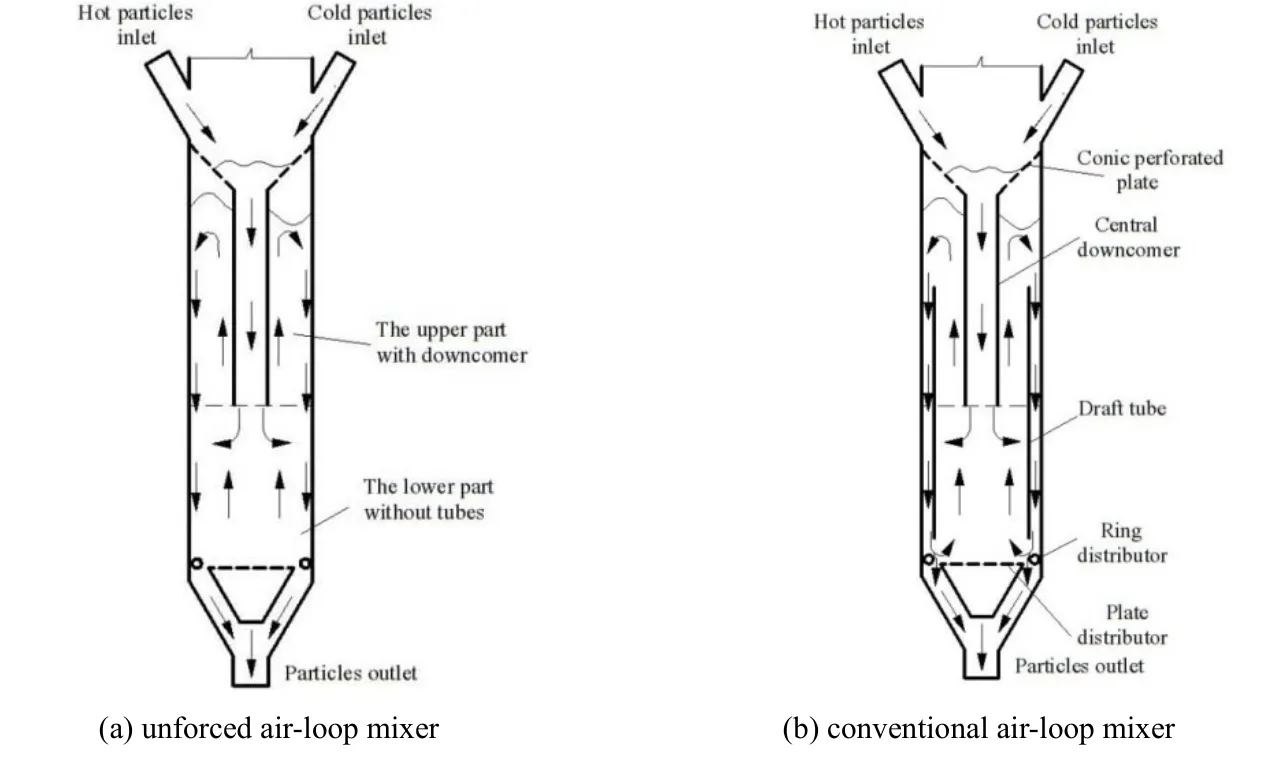
图2 混合器分区及结构Fig.2 Diagram of different regions in the mixers

1.2 计算工况

模拟条件为常温常压，采用空气作为气相，固相为流化催化裂化（FCC）催化剂颗粒，密度为1 498 kg/m3，堆积密度为937 kg/m3，终端速度为0.58 m/s，平均粒径为79 μm，实验中的粒度分布如表1所示。中心流化风由板式分布器进入混合器，表观速度分别为0.3，0.35，0.4 m/s (以混合器横截面积为基准，以下类同)，边壁区流化风由环形分布器进入混合器，表观速度为0.04 m/s。颗粒进料量为 11.7 kg/(m2·s)。

表1 实验中FCC颗粒粒度分布Table 1 Distribution of FCC particle size in experiment

2 数学模型

2.1 控制方程

采用双流体模型中的方程作为基本控制方程，包括连续性方程、动量守恒方程、颗粒温度方程等。详细的动力学方程可参见FLUENT®6.3.26的帮助文档及相关文献[11,12]。

2.2 曳力模型

相间动量主要考虑相间曳力，采用基于结构的EMMS曳力模型[13]，具体如下所述。

β为均匀化曳力系数[14,15]，关联式如下所示：

Cd的表达式为：

其中，Hd为非均匀结构因子，作为衡量结构对曳力系数的影响程度[5]。通过EMMS曳力模型[13]，获得Hd与床层空隙率（εg）的关系曲线，其相关拟合方程如表2所示，拟合度因子均在0.99以上。

表2 非均匀结构因子拟合方程HdTable 2 Fitting equation of Hd

2.3 边界条件

采用Gambit®2.4进行网格及构体划分。如图3(a)所示，混合器底部分布器区以及中部锥形筛板区采用非结构化网格，其他区域采用结构化网格，其中横截面网格分布如图3(b)所示，混合器总网格数约为58万，通过对Liu[2]的实验进行模拟，对网格无关性及模型进行了验证，如图4所示。

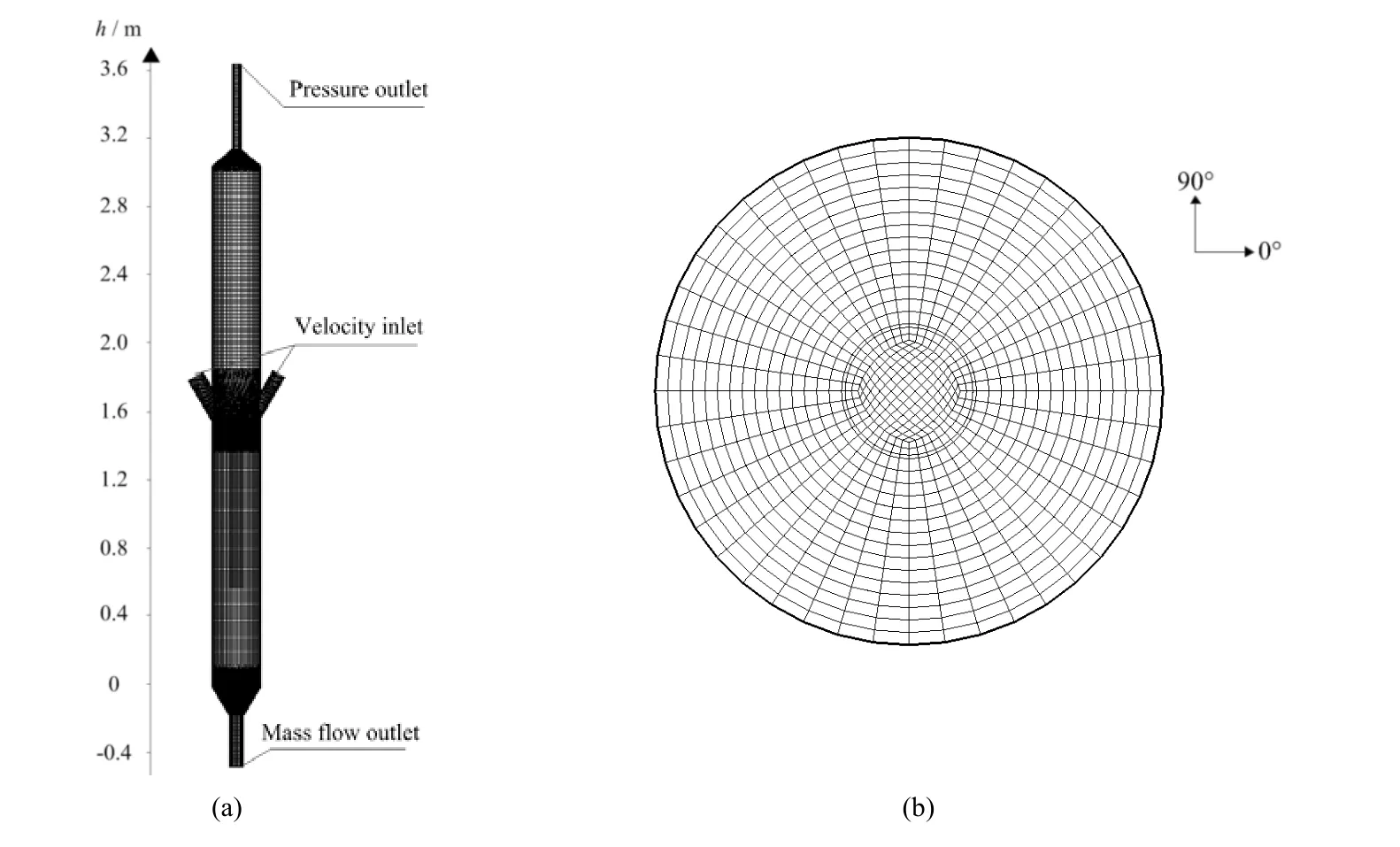
图3 构体网格分布Fig.3 Mesh distribution of configuration

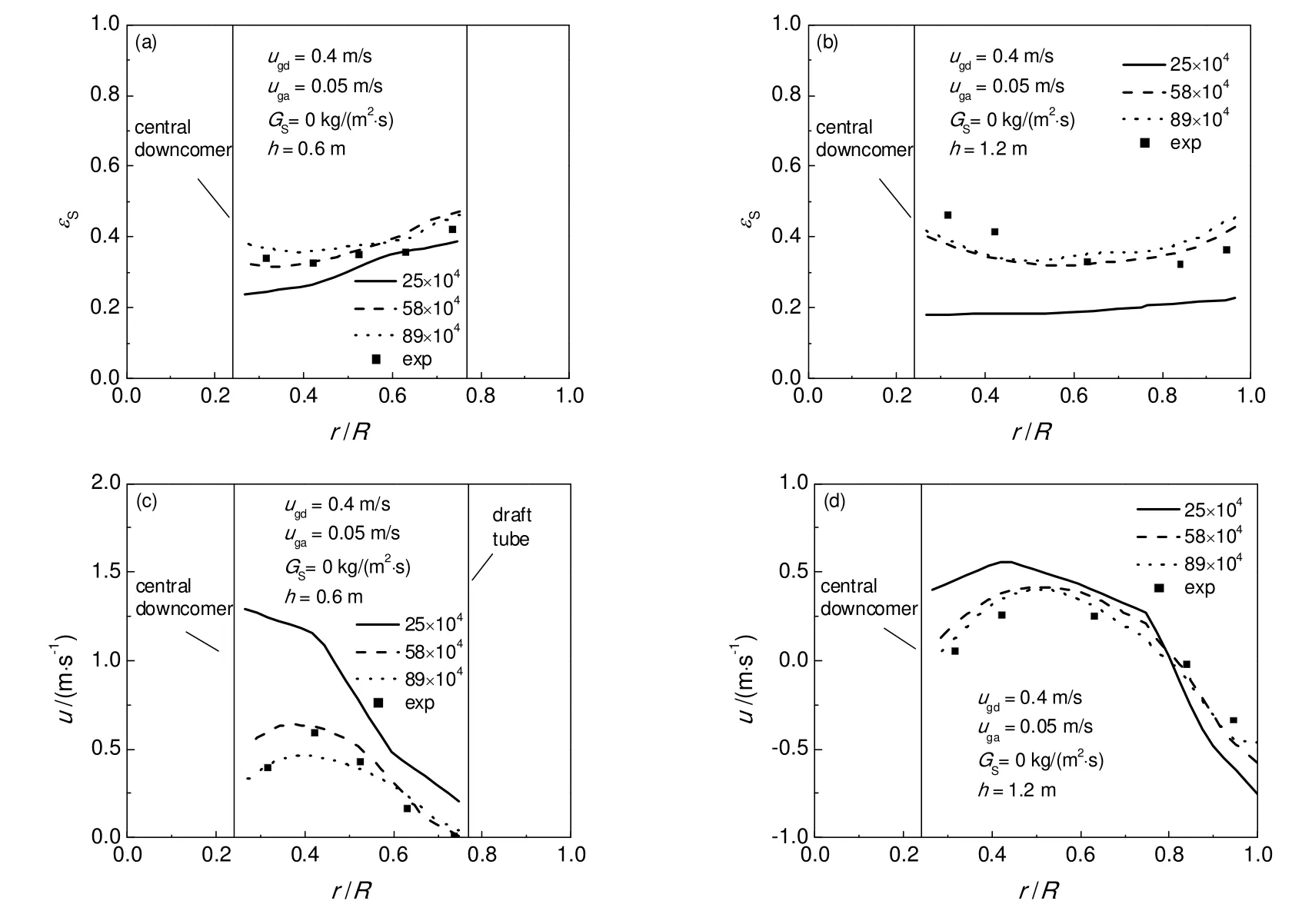
图4 环流混合器中模型验证Fig.4 Model validation in the gas-solid air loop mixer

模拟过程中，将分布器进行了简化，直接均匀进气，颗粒进口设为速度进口，气体出口为压力出口，混合器底部固体出口设为质量流率出口，出口的质量流率与进入混合器总的固体质量流率相等。壁面边界条件：气相设为无滑移，固相采用Johnson和 Jackson边界条件[16]，镜面系数设为 0.5[17,18]。Benyahia 等[19]研究认为，在大多数的流域中，可以采用层流气体粘度，并且Benyahia等[19]发现在中等密度的流动条件下，忽略气相湍流应力并不会对时均流动分布产生明显的影响。因此，为了使计算能够更好的收敛，限制可调变量数，本工作采用了层流模型。为了保证计算收敛，时间步长设为0.000 3 s，每一步最大迭代次数为40次。模拟时间设为40 s，充分保证了装置的运行稳定。时均数据为30～40 s的平均值，其它参数设置如表3所示。

表3 模拟参数设置Table 3 Simulation parameters

3 模拟结果与讨论

3.1 颗粒轴向速度分布

3.1.1 下部空管区颗粒轴向速度分布

如图2所示，板式分布器至中心下料管出口截面之间的区域为下部空管区，该区域受到中心下料管的进料、底部分布器进气等多种因素的影响，因此流场较为复杂。图5给出了下部空管区颗粒速度矢量图，可以看出颗粒的运动基本上可以分为上行和下行两个区域。其中上行区位于混合器中心，由于中心流化风流量较大，在气流的作用下中心处的颗粒主要向上运动。下行区靠近边壁，由于边壁流化风的气量较小，边壁附近的颗粒向下流动。由于上行区与下行区之间没有导流筒的阻挡，在两个区域之间不断有颗粒的交换。当下行区颗粒运动至分布器附近时，一部分颗粒经两个分布器之间的缝隙流出混合器，还有一部分颗粒沿径向向中心处运动，形成了颗粒的内循环。这部分颗粒在沿径向运动的过程中，与原上行区的颗粒进行混合，然后逐渐被气体夹带向上运动。尤其是在射流能够影响到的区域（r/R＜0.685），由于射流剧烈的扰动作用，大大强化了环流颗粒和中心处颗粒的混合。由图5还可以看出，中心处向上运动的颗粒与中心下料管向下流入的颗粒逆流接触，再次实现剧烈的混合，混合后的颗粒向边壁运动，这种沿径向的运动进一步促进了颗粒沿径向的混合。

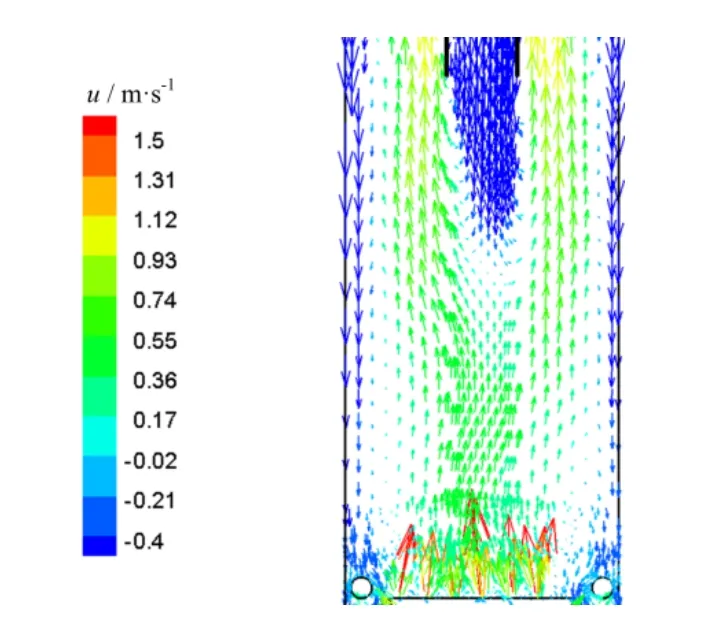
图5 下部空管区颗粒时均速度矢量Fig.5 Diagram of time-averaged particle velocity vector in the lower part without tubes

图6给出了下部空管区不同截面上颗粒轴向速度沿径向的分布。图6(a)所示截面距离板式分布器的距离仅为 40 mm，颗粒的流动受中心的板式分布器（Rp/R=0.685）和边壁附近的环管分布器（Rr/R=0.88）影响较大。在-0.5＜r/R＜0.5的区域，颗粒向上运动，速度分布较为均匀，可以看到分布曲线中有许多小的尖峰，这是受到了射流的影响。在 0.5＜|r/R|＜0.685的区域，随着径向位置的增加，颗粒速度逐渐减小，这一区域已经靠近板式分布器的外缘，布孔没有中心处密集。在 |r/R|为0.75附近颗粒速度出现极小值，这是由于该区域处于两个分布器之间，颗粒经缝隙向下运动流出混合器。在环形分布器上方投影区（0.75＜|r/R|＜0.9），由于环形分布器的阻挡，颗粒向下的速度逐渐减小。在靠近壁面附近（0.9＜|r/R|＜1），颗粒由环形分布器与混合器壁之间的缝隙流出混合器，颗粒向下运动的速度稍有增加。由图6(a)还可知，随着表观气速的增加，中心处颗粒向上运动的速度增加，边壁处颗粒向下运动的速度增加，循环速度的增加，将会提高颗粒在混合器内部的循环次数，有利于增加混合器的混合效率。

图6 下部空管区不同操作条件下的时均轴向速度分布Fig.6 Distributions of time-averaged axial particle velocity with different conditions in the lower part without tubes

图6(b) 给出了h为0.41 m处颗粒轴向速度分布，该截面与中心下料管出口截面（h为0.558 m）相距较近，受中心下料管进料的影响比较大。由图6(b)可知，在r/R为0附近，颗粒速度小于0，这是颗粒由中心下料管向下流入下部空管区造成的。随着径向位置的增加，颗粒速度先增加后减小，当|r/R|大于0.8时，颗粒改变方向，向下运动。

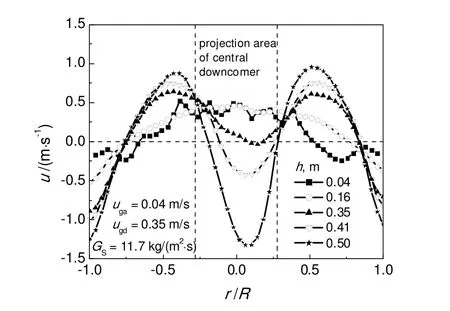
图7 下部空管区不同截面的时均颗粒轴向速度分布对比Fig.7 Comparisons of time-averaged axial particle velocity at different cross-sections of the lower part without tubes

图7给出了下部空管区颗粒轴向速度分布随高度的变化。由图7可知，在下部空管区，由于进料的影响，颗粒轴向速度在中心区随着高度的增加，逐渐减小，并且在h为0.35 m 的截面附近，中心区的颗粒速度接近 0，表明在此条件下，由中心下料管进入混合器的颗粒所能到达的截面高度为h为0.35 m，同时可以看出，在混合器中心下降的颗粒所处的范围与中心下料管下方投影区范围（-0.265＜r/R＜0.265）近似相等。在混合器边壁区（0.8＜|r/R|＜1），颗粒向下运动，随着高度的减小，颗粒向下的速度逐渐减小，这是由于底部区，颗粒运动受气体以及分布器的阻力增加。对比h为0.04 m 与其它截面上颗粒速度分布，发现颗粒在h为0.04 m的截面上边壁区的范围要明显偏大，这是因为在边壁向下运动的颗粒到达底部区时会沿着径向向中心移动，如图5所示。

3.1.2 上部下降管区颗粒轴向速度分布

上部下降管区为中心下料管出口截面与锥形筛板之间的区域（如图2(a)所示）。在该区域，气体经锥形筛板上的孔流出，而颗粒沿边壁向下运动。图8给出了上部下降管区颗粒速度矢量图，可以看出中心区和边壁区的两区流动结构依然存在，颗粒在向上运动的过程中不断的向外侧运动，与边壁区的下行颗粒逐渐混合，同时，少量颗粒被气体携带离开密相床层（h为1.3 m）至锥形筛板下方，受到锥形筛板阻挡后流至边壁区附近，而后改变方向向下运动。

在传统的环流混合器中，颗粒只能在导流筒上方沿径向流入边壁区，而在非强制环流混合器中，没有导流筒的阻挡，颗粒在不同截面上都能够沿径向流入边壁区，实现了颗粒多次径向混合，将有助于提高颗粒的混合效率。

图9为上部下降管区不同高度截面颗粒轴向速度的分布。图9(a)为h为0.66 m的截面，可以看出，在中心区（0.26＜|r/R|＜0.8），颗粒向上运动，在混合器壁面附近（|r/R|＞0.8），颗粒向下运动。由于壁面效应，靠近中心下料管壁面（|r/R|=0.26），颗粒速度较小，随着径向位置的增加，颗粒速度先增加后减小。由图9(a)还可以看出，随着表观气速的增加，颗粒向上的速度逐渐增加，而边壁区的范围逐渐减小。

图8 上部下降管区颗粒时均速度Fig.8 Diagram of time-averaged particle velocity vector in the upper part with downcomer

图9 上部下降管区不同高度的时均颗粒轴向速度分布Fig.9 Distributions of time-averaged axial particle velocity with different conditions in the upper part with downcomer

图9(b)为h为1.16 m的截面颗粒轴向速度分布，与h为0.66 m处（图9(a)）的速度相比，沿径向的分布相似，而中心处向上的颗粒速度与边壁区向下的颗粒速度均减小。随着表观气速的增加，颗粒向上的速度有所增加，但边壁区的范围变化并不明显。

图10给出了上部下降管区颗粒轴向速度分布随高度的变化。由图10可知，随着高度的增加，中心处颗粒向上的速度与边壁区向下的速度均逐渐减小，并且随着高度的增加，颗粒边壁区的范围由0.8＜|r/R|＜1 减小为 0.9＜|r/R|＜1。不同表观气速时的结果表明，随着表观气速的增加，边壁区的范围随着轴向高度的增加变化幅度减小。由图10还可以看出，随着轴向高度的增加，颗粒速度沿径向的分布更加均匀。

图10 上部下降管区不同截面的时均颗粒轴向速度分布对比Fig.10 Comparisons of time-averaged axial particle velocity at different cross-sections of the upper part with downcomer

图11 下部空管区不同截面颗粒时均速度矢量图Fig.11 Diagram of time-averaged particle velocity vector at different cross-section of the lower part without tubes

3.2颗粒径向速度分布

3.2.1 下部空管区颗粒径向速度分布

图11给出了下部空管区不同高度截面的颗粒速度矢量图。由图11(a) 可知，在靠近分布器的截面（h为0.04 m），边壁区的颗粒向中心运动，从而实现颗粒在混合器内部的循环。同时，颗粒向中心的运动，强化了颗粒沿径向的混合。图11(b)为h为0.16 m 截面的颗粒速度矢量图，与h为0.04 m的截面相比，中心处的颗粒向边壁区运动，同时颗粒在该截面还存在沿周向的运动，促进了颗粒在该区域的混合。图11(c) 为h为0.41 m截面的颗粒速度矢量图，在该截面，向上运动的颗粒与中心下料管向下流入的颗粒逆向混合，如图5所示，混合后的颗粒沿径向向外侧运动，增加了颗粒沿径向的混合。同时，由图11(b)和图11(c)还可以看出，从中心下料管进入混合器下部空管区的颗粒出现了偏流，这是因为颗粒是由0度方向进入锥形筛板上方的，在锥形筛板上方的床层中形成了偏流，进而影响到中心下料管中的流动。此外，由于中心下料管直径相对较大，一部分气体窜入了中心下料管，进一步加剧了下料管中的偏流现象。当颗粒由中心下料管流出后，先向下运动一段距离，然后才会改为向上流动。由图11(b)和图11(c)可以看出，在高度h为0.16 m和0.41 m的截面上，都可以观察到由于偏流所引起的颗粒沿周向的运动，而由图11(a)可以看出，高度为h为0.04 m的截面距离下料管出口较远，基本不受偏流的影响，该区域的流场主要受到气体分布器射流的控制。

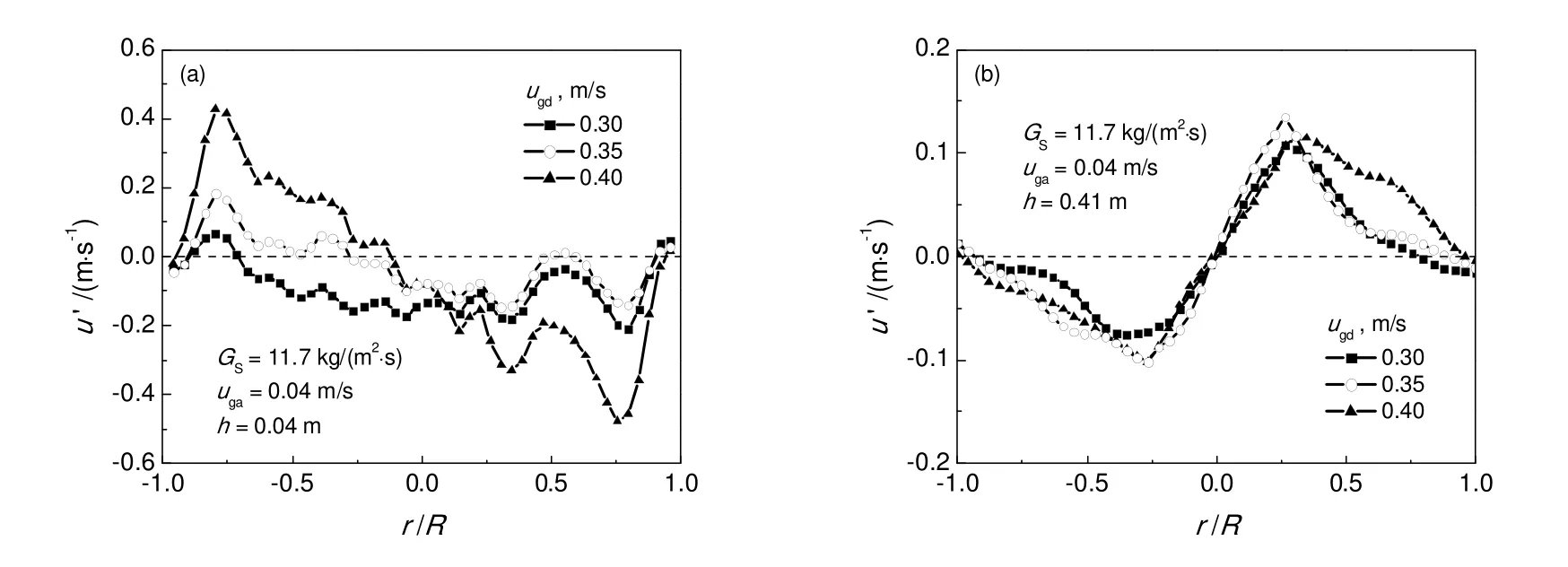
图12 下部空管区时均颗粒径向速度分布Fig.12 Distribution of time-averaged radial particle velocity in the lower part without tubes

图12(a)与图12(b)分别给出了h为0.04 m截面以及h为0.41 m截面的颗粒径向速度分布，本文规定指向0 °的方向（冷颗粒进料一侧）为正方向。由图12(a)可知，在-1＜r/R＜0的区域，速度为正，颗粒向中心处（r/R=0）运动，而在0＜r/R＜1的区域，速度为负，颗粒也向中心处（r/R=0）运动。由边壁到中心，颗粒速度先增加后减小，在两个分布器之间的区域（|r/R| =0.75），速度最大。同时，由图12(a)还可以看出，表观气速越小，颗粒运动的速度也越小。在高气速时，-0.75＜r/R＜0内的颗粒从边壁流向中心，当ugd为0.3 m/s时，-0.75＜r/R＜0的颗粒改为向边壁运动，表明较小的气速不利于颗粒的环流。由图12(b)可知，由中心向边壁，颗粒速度先增加后减小，在中心下料管边壁投影区附近（|r/R| =0.26）取得极值，这是因为两股颗粒的逆流混合造成了颗粒沿径向的运动（如图5所示）。

图13对比了下部空管区颗粒径向速度在不同截面的分布。由图13可知，在h为0.04 m的截面，颗粒由边壁区向中心区流动，而在h为 0.25 m和0.41 m的截面，颗粒沿径向运动的方向与h为0.04 m时的相反，由中心区向边壁区运动，并且随着轴向高度的增加，沿径向运动的速度增加。

图13 下部空管区不同截面时均颗粒径向速度分布Fig.13 Distribution of time-averaged radial particle velocity at different cross-sections of the lower part without tubes

3.2.2 上部下降管区颗粒径向速度分布

图14给出了上部下降管区不同高度截面的颗粒速度矢量图，可以看出，在不同截面，颗粒有相似的径向和周向运动。这说明中心下料管颗粒进料的偏流作用还没有消失，使得颗粒在水平截面产生了周向旋转运动。颗粒沿径向及周向的运动将有效增加颗粒在水平方向的混合。图15给出了上部下降管区颗粒径向速度在不同操作条件下的分布。由图15(a) 可知，在h为0.66 m的截面上，颗粒由中心向边壁运动，并且随着径向位置的增加，颗粒径向速度先增加后减小，在r/R为0.75附近，速度达到最大值，随着表观气速的增加，颗粒速度增加。h为0.91m截面上的颗粒速度分布与h为0.66 m的截面上的相似，如图15(b) 所示。在传统环流混合器中，导流筒中以及边壁区的颗粒速度近似为平推流，该区域对颗粒的混合贡献较低，与之相比，非强制环流混合器中颗粒沿径向及周向的运动（如图14所示），将显著增加颗粒在水平方向的混合，提高混合效率。

图14 上部下降管区不同截面颗粒时均速度矢量Fig.14 Diagram of time-averaged particle velocity vector at different cross-section of the upper part with downcomer

图15 上部下降管区的时均颗粒径向速度分布Fig.15 Distribution of time-averaged radial particle velocity in the upper part with downcomer

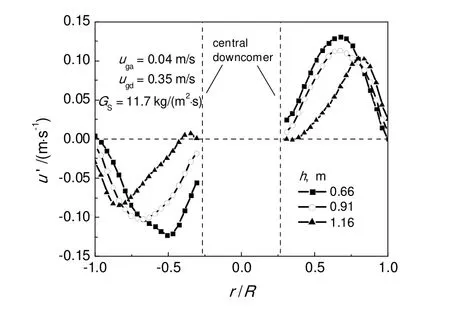
图16 上部下降管区不同截面的时均颗粒径向速度分布Fig.16 Distribution of time-averaged radial particle velocity at different cross-sections of the upper part with downcomer

3.2.3 径向速度分布随高度的变化

图16对比了上部下降管区颗粒径向速度在不同截面的分布。由图可知，随着高度的增加，速度逐渐减小，并且颗粒速度极大值向边壁处移动。

4 结 论

基于EMMS曳力模型，采用CFD模拟的方法考察了非强制环流混合器内不同区域颗粒速度在不同操作条件下的分布规律，得出了如下结论：

a）导流筒限制消失，颗粒在中心区与边壁区之间流入与流出，增加了颗粒的混合。由于中心下料管进料的偏流作用，颗粒在上部下降管区以及h为0.16 m附近截面产生了明显的沿周向运动。

b）在下部空管区，边壁区的范围受高度及表观气速的影响不大，而在上部下降管区，边壁区的范围随着表观气速及轴向高度的增加而减小。

c）中心下料管下方投影区，向下的颗粒速度随着高度的减小而减小。

d）靠近分布器的区域（h=0.04 m），颗粒由边壁区向中心区运动，其它高度下，颗粒沿径向向外侧运动。

模拟结果可为环流混合器结构的进一步优化提供了依据。

符号说明

Cd—— 单颗粒（气泡）曳力系数

d—— 直径，m

G—— 循环强度，kg/(m2·s)

Hd—— 非均匀结构因子

h—— 以分布板为基准的轴向高度，m

R—— 筒体内半径，m

Rp—— 分布板半径，m

Rr—— 环形分布器半径，m

Re—— 雷诺数

r—— 半径 / m

u—— 颗粒轴向速度，m/s

ugd—— 中心区表观气速，m/s

uga—— 边壁区表观气速，m/s

u’—— 颗粒径向速度，m/s

v—— 颗粒（气体）真实速度，m/s

β—— 均匀曳力系数，kg/(m3·s)

βe—— 基于结构的曳力系数，kg/(m3·s)

εg—— 空隙率

εs—— 固含率

μ—— 粘度，Pa·s

ρ—— 密度，kg/m3

下标

g—— 气体

p—— 颗粒

s—— 固体

[1]Fang M, Luo K, Yang S, et al.Computational Fluid Dynamics-Discrete Element Method Investigation of Solid Mixing Characteristics in an Internally Circulating Fluidized Bed [J].Industrial & Engineering Chemistry Research, 2013, 52(22):7556-7568.

[2]Liu M, Xie J, Meng Z, et al.Hydrodynamic Characteristics and Mixing Characteristics of a New Type Particle Mixer [J].Journal of Chemical Engineering of Japan, 2015, 48(7):564-574.

[3]张博峰, 秦迪, 孟振亮, 等.无序环流混合器的流体力学特性和颗粒混合特性 [J].化学反应工程与工艺, 2017, 33(2):104-115.Zhang Bofeng, Qin Di, Meng Zhenliang, et al.Hydrodynamics and particle mixing characteristics of a disordered air-loop mixer without draft tube [J].Chemical Reaction Engineering and Technology, 2017, 33(2):104-115.

[4]Mostoufi N, Chaouki J.Local Solid Mixing in Gas-Solid Fluidized Beds [J].Powder Technol, 2001, 114(1):23-31.

[5]Wang W, Li J H.Simulation of gas-solid two-phase flow by a multi-scale CFD approach—extension of the EMMS model to the sub-grid level [J].Chem.Eng.Sci., 2007, 62(1-2):208-231.

[6]Shi Z, Wang W, Li J H.A bubble-based EMMS model for gas-solid bubbling fluidization [J].Chem Eng Sci, 2011, 66 (22):5541-5555.

[7]Lungu M, Wang J D, Yang Y R.Numerical Simulations of a Bubbling Fluidized Bed Reactor with an Energy Minimization Multiscale Bubble Based Model: Effect of the Mesoscale [J].Ind Eng Chem Res, 2014, 53 (42):16204-16221.

[8]Wang S, Lu H, Li D, et al.Simulation of the Chemical Looping Reforming Process in the Fuel Reactor with a Bubble-Based Energy Minimization Multiscale Model [J].Energ Fuel, 2013, 27 (8):5008-5015.

[9]Zhang N, Lu B, Wang W, et al.Virtual experimentation through 3D full-loop simulation of a circulating fluidized bed [J].Particuology,2008, 6 (6):529-539.

[10]Mei Y, Zhao M, Lu B, et al.Numerical comparison of two modes of circulating fluidized bed (CFB) operation: Fluid catalytic cracking vs CFB combustor [J].Particuology, 2017, 31 (2):42-48.

[11]Gidaspow D.Multiphase Flow and Fluidization: Continuum and Kinetic Theory Description [M].Boston: Academic Press, 1994.

[12]Sinclair L, Jackson R.Gas-particle flow in a vertical pipe with particle-particle interactions [J].AIChE Journal, 1989, 35(9):1473-1496.

[13]Hong K, Shi Z S, Wang W, et al.A structure-dependent multi-fluid model (SFM) for heterogeneous gas-solid flow [J].Chem.Eng.Sci.,2013, 99:191-202.

[14]Ergun S.Fluid flow through packed columns [J].Chemical Engineering Process, 1952, 48(2):89-94.

[15]Wen C Y, Yu Y H.Mechanics of fluidization [J].Chemical Engineering Symposium Series, 1966, 62:100-111.

[16]Johnson P C, Jackson R.Frictional-collisional constitutive relations for granular materials, with application to plane shearing [J].J.Fluid Mech.1987, 176:67-93.

[17]Li T, Benyahia S.Evaluation of wall boundary condition parameters for gas-solids fluidized bed simulations [J].AIChE Journal, 2013,59(10):3624-3632.

[18]Li T, Benyahia S.Revisiting Johnson and Jackson boundary conditions for granular flows [J].AIChE Journal, 2012, 58(7):2058-2068.

[19]Benyahia S, Syamlal M.O'Brien T J.Study of the ability of multiphase continuum models to predict core-annulus flow.AICHE Journal,2007, 53(10): 2549-2568.