空仓工况下群仓中各单仓动力相互作用分析
王树明++张大英


2
摘要:为研究群仓中各单仓之间的动力相互作用,以上海外高桥某储存粮食用群仓为背景,制作了2行3列共6个单仓组成的群仓模型,群仓模型具有钢板顶盖以模拟实际中的仓上建筑物,具有刚性底座以模拟实际中的基础结构。通过对空仓工况下的群仓模型进行有限元数值分析,得到了其各阶模态,对模型前五阶模态振型进行分析,结果表明,群仓模型前两阶模态振型为6个单仓一起沿群仓整体对称轴的弯曲变形,单仓之间动力相互作用可以忽略,而且前两阶模态振型相互正交。群仓模型第三阶模态振型为6个单仓绕群仓整体平面中心的扭转变形,同时伴随有4个角仓的弯曲变形,由于中间仓受约束程度强,其动力反应微弱;群仓模型第四阶、第五阶模态振型主要体现为4个角仓的局部变形,而不再是6个单仓的整体变形,单仓因所处位置不同受约束程度不同,动力反应大小不同;群仓模型的第三阶及以上模态振型体现了单仓之间的不同约束程度及动力相互作用。
关键词:群仓;空仓工况;动力相互作用;数值分析
中图分类号:TU317+.1;TU359 文献标识码:A 文章编号:0439-8114(2017)09-1742-03
DOI:10.14088/j.cnki.issn0439-8114.2017.09.035
Dynamic Interaction Analysis of the Individuals Belong to Empty Group Silos
WANG Shu-ming1,ZHANG Da-ying2
(1. Henan Orient Architectural Design Co., Ltd., Zhengzhou 450003, China;
2. School of Civil Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450015, China)
Abstract: In order to study dynamic analysis of the individuals belong to empty group silos,a group silos model was made based on a granary in Shanghai Waigaoqiao. It has 6 silos with 2 rows and 3 columns. A steel plate was designed for simulating buildings on top of the group silos, and a rigid base was designed for simulating its foundation. Then FEM was used to obtain its modes,and the first five mode shapes were analyzed. The results showed that the 6 individuals bend along the axis of the group silos together with each other in the first two orthogonal modes,therefore,the dynamic interactions are ignored. For the third mode, it is mainly the torsional deformation of the 6 individuals around the plane centre of the group silos,simultaneously, the four silos in the corner bend,but the dynamic response of the middle silos is weak due to the constraint of the other silos. For the fourth and the fifth modes,it is mainly local deformations of the four silos in the corner,but not the overall deformation. What's more,the dynamic response is different for the 6 silos due to their positions. Then it follows that the different constraints and dynamic interactions among the 6 silos are reflected by the third mode and above.
Key words: group silos;empty silos;dynamic interaction;numerical analysis
用以存儲粮食、煤炭等的立筒仓结构,结构形式简单、刚度大,广泛应用到各个行业中。有大直径的单仓,也有多个单仓成排组成的排仓(多用于存储煤炭),或是多个单仓组合成的m行n列的群仓,其中群仓所占比例较大,这是由于立筒群仓与单仓相比,整体刚度大,组成群仓的各个单仓之间的星仓亦可储料,故而存储物料更多。鉴于立筒仓的诸多优点及工程中的广泛应用,相关学者也对其做了诸多研究,主要包括以下几个方面,单仓、排仓的自振特性研究[1-5],筒仓内储料流动问题、储料侧压力研究[6-8],筒仓仓体的振动问题研究[9],单仓的动力测试、动力参数识别、地震反应分析等研究[10-12]。从这些研究报道可以看出,对于立筒仓的研究尤其是群仓动力问题的研究一直处于发展当中,至今没有统一的认识和成熟的计算理论供研究计算和工程设计所用。目前,工程中常利用单仓的抗震方法并加强构造措施对群仓进行设计验算。
分析表明,群仓和单仓的区别是很大的,群仓由多个单仓组成,各个单仓之间仓体包括支撑体系整体相连,各个单仓间由于位置和连接的不同是否存在显著的动力相互作用是值得关注的问题。因此,笔者对一空仓工况下的钢筋混凝土立筒群仓模型进行数值模拟分析,通过分析各阶振型中组成群仓的各个单仓的振型形态,研究群仓中位置不同单仓的不同振型形态及单仓之间的动力相互作用问题,为这方面的研究提供参考。
1 群仓模型概况
1.1 群仓模型
为研究钢筋混凝土立筒群仓中各单仓之间的动力相互作用,采用河南工业大学土木建筑学院仓储结构理论与分析課题组在国家自然科学基金项目(50678061)中进行地震模拟振动台试验的群仓模型,此模型是以上海外高桥柱支承粮食立筒群仓为背景,利用相似理论方法制作的,模型与实际群仓的几何尺寸相似比例为1/16。群仓由2行3列共6个单仓组成,为双轴对称结构,柱支承结构体系,单漏斗口卸料。原型结构立筒群仓材料为钢筋混凝土结构,因此模型材料采用的是微粒混凝土和镀锌铁丝网。
此外,根据试验条件并保证结构抗侧刚度的前提下,对仓顶和基础作了简化处理。原型结构立筒群仓顶部为仓上建筑物,制作模型时利用钢板作为其顶盖。对于群仓基础简化为十字交叉的梁板结构刚性底座,底座的抗弯、抗冲切、锚固能力及整体刚度符合规范要求。刚性底座配筋计算荷载为上部模型结构重量加底座全部重量之和,再乘以动力放大系数1.5。图1所示为群仓模型。
1.2 模型数据
通过试验测得微粒混凝土的弹性模量为8.983×103 MPa,重度为0.02 MPa。群仓中各单仓尺寸、配筋均相同,每个单仓均有12根截面为0.05 m×0.05 m的柱子支承,各个单仓在连接处为整浇(包括仓壁和柱子)。群仓中单仓总高度2.5 m、仓壁高度 2 m、支承高度0.5 m、仓壁外直径0.778 m、仓壁厚度0.014 m。
2 数值分析
2.1 单元类型和计算参数
采用ANSYS软件对群仓模型进行模态分析,所用单元类型包括模拟薄壁结构的SHELL63单元和模拟梁类构件的BEAM188单元。各主要构件的单元类型包括①SHELL63单元:顶盖板、各单仓仓壁、各单仓漏斗;②BEAM188单元:钢板顶盖底部的十字交叉梁、环梁、柱子。
模拟时不考虑镀锌铁丝的作用,故而弹性模量按微粒混凝土的弹性模量值8.983×103 MPa输入,重度按0.02 MPa输入,泊松比取0.2。
2.2 模态振型
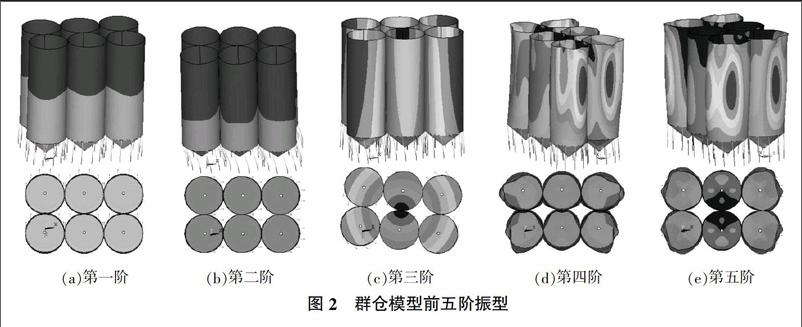
通过有限元方法分析得到了立筒群仓模型的前若干阶频率和振型结果,由于本研究的目标是分析组成群仓的各个单仓的动力相互作用,故而不对频率作分析,仅取前五阶振型结果进行分析。图2为群仓模型前五阶振型的立面和平面图。
从群仓模型的第一阶、第二阶振型可以看出,各个单仓的振型形态一致,与单仓在群仓中的位置无关,而且相互之间不存在挤压变形,振型形态都表现为各个单仓向同一方向的群仓整体变形。第一阶振型与第二阶振型为正交关系,前者为群仓整体沿短对称轴方向的变形,后者为群仓整体沿长对称轴方向的变形。此外,前两阶振型不同的是第一阶振型中各个单仓动力反应较大范围占据了仓壁的1/2,第二阶振型中各个单仓动力反应较大范围约占据了仓壁的2/3。由上述分析可知,若只考虑前两阶模态,对于群仓的动力计算模型利用二维多质点悬臂杆件(图3)适宜。
从群仓模型的第三阶振型可以看出,组成群仓的各单仓振型形态不完全相同,四个角仓振型形态相同,两个中间仓振型形态相同,相邻两个单仓之间均不存在相互挤压,整体振型形态为6个单仓绕群仓平面几何中心的扭转(由振型图可以看出动力反应最弱位置在其平面几何中心)。由于单仓在群仓中的位置不同,受约束程度不同,因此,中间仓整体动力反应都弱于角仓。另外,相邻单仓仓壁及柱子均浇筑成整体,因此这些部位相互约束,增强了整体刚度,而角仓远离连接处的部位受约束程度小,故而动力反应较大。由上述分析可知,若考虑前三阶模态,对于群仓的动力计算模型则不能简单简化为图3所示的二维多质点悬臂杆件,需要考虑其为三维空间模型更加适宜。
从群仓的第四阶、第五阶振型可以看出,组成群仓的各单仓振型形态不完全相同,同第三阶类似,都表现为四个角仓振型形态相同,两个中间仓振型形态相同。与前三阶振型不同的是,整体振型形态不明显,主要体现为四个角仓仓壁的弯曲、剪切变形。第四阶振型中角仓的弯曲、剪切变形较大的范围小于第五阶振型中的角仓。此外,两阶振型中,中间仓的振型形态都不明显,而且第五阶中间仓的反应更弱于第四阶。由上述分析可知,若考虑前五阶模态,对于群仓的动力计算模型亦不能简化为图3所示的二维多质点悬臂杆件,需要考虑其为三维空间模型更加适宜。
3 小结
为研究立筒群仓结构中各单仓之间的动力相互作用,设计了2行3列共6个单仓组成的微粒混凝土镀锌铁丝网群仓模型,模型顶为钢板顶盖,模型底为刚性支座。
通过对上述柱支承结构体系立筒群仓模型在空仓工况下的有限元数值模拟研究,得到以下结论。
1)由群仓模型的前两阶振型图分析可知,若对群仓进行动力计算,当仅考虑前两阶模态时可忽略单仓之间的动力相互作用,不考虑相邻单仓的相互约束,将群仓简化为二维多质点悬臂杆件。
2)由群仓模型的第三阶、第四阶、第五阶振型图分析可知,若对群仓进行动力计算,当考虑前三阶或以上模态时,需要考虑单仓之间的动力相互作用及相邻单仓之间的相互约束,将群仓简化为二维多质点悬臂杆件不够合理,需要考虑群仓为具有相互约束的三维空间模型结构。
参考文献:
[1] 刘增荣,黄 义.贮仓结构参数的频域识别[J].振动与冲击,2001, 20(1):79-81.
[2] 黄 义,尹冠生.考虑散粒体与仓壁相互作用时筒仓的动力计算[J].空间结构,2002,8(1):3-9.
[3] 王命平,孫 芳,高立堂,等.筒承式群仓的地震作用分析及试验研究[J].工业建筑,2005,35(10):29-32.
[4] 王瑞萍,王命平,迟 嵘.相互作用对筒承式简仓自振基频的影响[J].青岛理工大学学报,2006,27(2):21-23.
[5] 滕 锴,王命平,耿树江.筒承式群仓有限元分析及自振基频的简化计算[J].特种结构,2006,23(4):34-36.
[6] PARISI D R,MASSON S,MARTINEZ J.Partitioned distinct element method simulation of granular flow within industrial silos [J].Journal of Engineering Mechanics,2004,130(7):771-779.
[7] RICCARDO A,ANDREA S,PAOLO C. Simulation of dense granular flows: Dynamics of wall stress in silos[J].Chemical Engineering Science,2009,64(18):4040-4050.
[8] 张大英,王树明,梁醒培.漏斗倾角对粮仓侧压力的影响[J].土木工程与管理学报,2016,33(5):28-32.
[9] FERNANDO G F,LUIS A G. Forced vibrations of silos leading to buckling[J].Journal of Sound and Vibration,1999,224(3):431-454.
[10] 张大英,王录民,王树明.立筒单仓模型动力测试与参数识别研究[J].结构工程师,2014,30(6):145-150.
[11] 张大英,王录民,许启铿.某煤仓在线测试技术与动力参数识别研究[J].地震工程与工程振动,2014,34(1):193-198.
[12] STEFAN H,KONSTANTIN M,ASCE M. Granular material silos under dynamic excitation:Numerical simulation and experimental validation[J].Journal of Structural Engineering,2006,132(10):1573-1579.

