一种改进的栅格星图识别算法*

钱华明， 郎希开， 李 猛

(1.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001；2.中航光电科技股份有限公司，河南 洛阳 471003)

一种改进的栅格星图识别算法*

钱华明1， 郎希开1， 李 猛2

(1.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001；2.中航光电科技股份有限公司，河南 洛阳 471003)

针对传统的栅格算法提取的特征模式不能反映其内在相似程度进而影响星图识别准确性的问题，提出了一种改进的栅格算法。利用特征模式间的度量函数反映不同特征模式之间的相似程度，解决了传统算法中由于位置量测误差造成的影响。根据实际情况建立了仿真环境，进行了仿真实验。结果表明：当星点位置噪声大于1.5像素时，改进算法的星图识别成功率明显高于现有的栅格算法；在存在“假星”的情况下改进算法的星图识别成功率优于现有的算法，验证了算法的有效性。

栅格算法； 特征模式； 相似程度； 度量函数

0 引 言

星敏感器是航天器完成航天任务的主要工作部件，为航天器提供高精度的姿态信息。利用星敏感器确定姿态的过程分为：星空拍摄、质心提取、星图识别和姿态计算4个步骤。星图识别的实质就是在星表中寻找与观测星图中观测星相对应的导航星[1]。星图识别技术是星敏感器的关键技术之一，识别速度和识别成功率是衡量星图识别算法的关键指标。

目前,常用的星图识别算法根据特征提取方式的不同可以分为两大类：子图同构类算法和模式识别类算法[2]。子图同构类算法把星敏感器得到的观测星图看成是全天球星图的子图，以恒星作为顶点，利用恒星的星等以及它们之间的角距等信息，以线段、三角形、多边形等作为基本元素来进行星图识别。三角形算法[3],多边形角距匹配算法,匹配组算法[4]等算法都属于这一类。模式识别类算法通过给观测星构建特征模式，在导航星库中寻找与观测星的特征模式最为相近的星。栅格算法[5]、基于统计特征的算法[6]为此类算法中具有代表性的算法。上述的算法中，三角形算法由于其算法结构简单、易于实现等优点应用最为广泛,但也存在着诸多缺点，比如所需的导航数据库大、匹配时间长、对噪声的鲁棒性较差。文献[7]中对三角形算法、匹配组算法与栅格算法的性能做了详细比较，结果表明栅格算法较传统的基于子图同构的三角形算法和匹配组算法在鲁棒性、存储容量和识别时间等方面有很大的优势。但是栅格算法中提取的恒星特征模式不能反映内在的相似程度，影响栅格算法的星图识别成功率[8]。

针对上述问题，本文将能够反映相似程度的度量函数引入到栅格算法中，通过观测星特征模式和导航星特征模式之间的度量函数值来确定模式向量的相似程度，从而降低了星点位置误差带对识别成功率降低的影响，提高了改进算法的鲁棒性和精度。

1 算法描述

1.1 栅格算法

栅格算法的模式生成过程如图1所示，可以分为以下几步[7,8]:

1)选择一颗待识别的观测星作为主星并确定模式半径pr。

2)平移选择的主星及邻域半径pr内的所有恒星，使主星位于视场中心。

3)确定近邻星，即在确定的模式半径pr内，邻域半径br外寻找距离主星最近的星。

4)以主星为坐标原点，主星与近邻星的连线为坐标轴，将星图进行旋转，使得近邻星位于x轴上。同时将星图划分成g×g栅格并生成长度为g2的特征模式向量v。观测星的特征模式用g×g栅格cell(m,n)来表示，如果某个栅格内有伴星，则其值为1，否则为0。每颗恒星的特征模式向量可以表示为v=(a1,a2,…,ak,…,ag)，k=1,2,…,g2，且有

(1)

式中m∈[1,g];n∈[1,g];k=(m-1)·g+n。

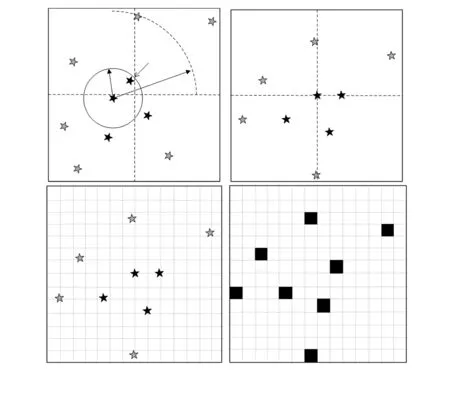
图1 原始栅格算法

假设拍摄星图中某观测星j的特征模式为patj,导航星表中所有导航星特征模式的集合为{patj}，则星图识别的实质即为寻找

(2)

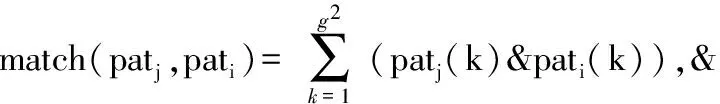
传统栅格算法提取的模式向量并不能反映内在的相似程度。图2为g=8的栅格，设其特征模式为pat，则根据栅格的特征模式构造原理，pat的第11，21，36，39，42，54个元素为1，其余的为0。但是由于星点位置误差的影响，位于栅格边缘的星可能由A位置移动到B位置。设此时构造的特征模式为pat′，则pat′的第11，21，36，39，43，54个元素为1，其余的为0。此时pat和pat′的特征模式明显不同，采用这种构造方式，相似分布的特征提取出来的特征模式差别很大，无法在特征空间反映出其相似程度，将直接影响识别算法的成功率，当星点位置误差较大时，产生的影响将显著增加，识别成功率将大幅降低。

图2 g=8的栅格

1.2 改进的栅格算法

假设拍摄星图中某观测星j的特征模式为patj，导航星表中所有导航星特征模式的集合为{pati}。pati和patj为将要比较的两个特征模式。对pati来说，某一个栅格内有伴星pati[m,n]=1，则在patj中离其位置最近的某个栅格中必有一颗星pati[m′,n′]=1。因此,某个栅格中pati[m,n]=1的度量函数可以这样计算

(3)

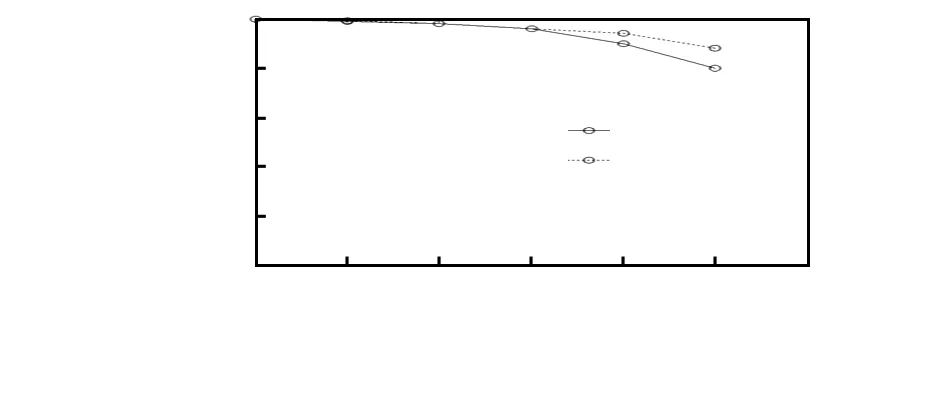
式中a

如果某个栅格内没有伴星pati[m,n]=0，则其度量函数为0，即cost(pati[m,n]=0)=0。

同理，对patj来说，某一个栅格内有伴星patj[m,n]=1，则在pati中离其位置最近的某个栅格中必有一颗星pati[m′,n′]=1。因此,某个栅格中patj[m,n]=1的度量函数为

(4)

式中a

如果某个栅格内没有伴星patj[m,n]=0，则其度量函数为0，即cost(patj[m,n]=0)=0。

分别对每一个pati和patj进行相应度量函数的计算，则在{pati}寻找观测星j所对应的导航星,即寻找

获取满足式(5)的最小pati后，可得导航星库中与观测星j所匹配的导航星。

从度量函数的构建过程可以得出：对于两个特征模式，如果二者相似度越大，则度量函数的值越小；如果相似度越小，则度量函数的值就越大。而对于正确匹配的两个特征模式，经过计算得到的度量函数值最小。因此，可以通过度量函数值的大小反映不同特征模式之间的相似程度，从而降低了星点位置误差对识别成功率的影响，表明了改进后的识别算法具有更强鲁棒性。

2 星识别模式表的存储和搜索方式

式(2)表示的匹配过程存在的显著问题是冗余匹配过多、效率太低。对选取后的导航星进行匹配，需要经过N×g2次运算(N为所选用的导航星数目)，而且g2远远大于视场内平均的恒星数量，显然该识别方法耗时非常大。针对这个问题，本文设计了一个查找表LT来存储导航星的特征模式，加快匹配速度[9]。

2.1 星识别模式

查找表包括g2项，标记为LTi,i=1,2,…，g2，分别对应于每个栅格。对于每个导航星，如果在栅格i中有伴星，则在LTi中增加一项记录，该记录存储的是这个主星的标号。按照此种方法，完成整个查找表的构建。在构建查找表的过程中，需要将同一项中重复出现的导航星编号去除。利用查找表来构建导航数据库结构如图3所示。在构建特征模式时，对于每一颗恒星，分别记录其伴星落在栅格内的位置标号，采用栅格内的位置标号来表示某颗导航星的特征模式。

图3 导航数据库结构图

2.2 搜索方式

利用查表进行匹配时，其匹配过程示意图如图4所示。以观测星S为例，假设星S的特征模式为(12,26，31，54，102，133)，则分别检索查找表LTi中的12,26,31,54,102,133项记录的导航星标号，选出导航星标号出现次数最多的导航星。经过检测，第454颗导航星匹配次数最多，将其记录为初始匹配星。

图4 查找过程

导航数据库建立之后，对观测星进行识别。于某一视场内选择亮度最亮的α颗星进行识别，文献[11]指出当星敏感器视场为12°,星等阈值不小于6MV时，其平均捕捉恒星数为13.8颗。结合仿真选用的星敏感器,本文选取α=10，对于每一颗观测星，按照上述查找过程将导航星库中出现次数大于阈值ξ的导航星挑选出来作为候选匹配星，候选匹配星可能不唯一。然后把观测星的特征模式分别与候选匹配星的特征模式建立度量函数，度量函数值最小的匹配组为正确匹配的2个特征向量，即该导航星为观测星正确匹配的星。按照同样的方法对所有的α颗星进行识别，如果有2颗及以上的星点识别成功，即认为星图识别成功;否则,即为失败[6]。

3 仿真与分析

仿真中所用的基本星表是第谷第二星表(Tycho—2)，从中选取星等亮度大于7.0的星中筛选出5 404颗组成导航星表。

3.1 仿真条件设置

从1.1节中栅格算法原理可知，邻域半径br和栅格数目g共同决定栅格的形成，进而决定其性能。当g设置较大时，即量化等级较细，容易受星点位置噪声干扰使产生错误匹配的可能性增加，而且计算量也很大；当g设置较小时，多个星点目标出现在同一个栅格内的概率将增加，使得特征模式维数太低，达不到正常识别的要求。同理，br如果设置过大，虽然会使得识别算法对噪声的鲁棒性变强，但增加了近邻星出现在视场之外的概率，使得正确选取近邻星的概率降低，将直接影响到星图识别成功率。因此，不合适大小的g和br都会使识别成功率下降，需要对恒星在视场中的分布情况进行统计，然而根据统计结果来设置合理的栅格数目g和缓冲半径br。

本文中选取的星敏感器视场为12°×12°，星等敏感极限为7.0星等，分辨率为512×512。对选取的基本星表进行角距分布的统计。图5为5 000次随机视轴指向星点之间角距分布的统计结果分布图。

图5 星点之间角距分布统计

根据统计结果可以看出:星间角距中有99.9 %的角距大于0.3°，因此,选择栅格大小为0.3°，可以保证绝大多数星分布在不同的栅格中，栅格数目g=12°/0.3°=40。同理，选择邻域半径br=512/40=12.8像素。模式半径pr可以设置为星敏感器的视场大小，即pr=12°。度量函数参数a=0，b=2，c=4，k=2，匹配阈值ξ=5。

3.2 仿真结果

图6为星敏感器星等噪声σ=0.2时，本文提出的算法和传统算法的星图识别成功率随着位置噪声变化的曲线。

图6 识别成功率随星等噪声变化的曲线

从图6可以看出，当星点位置噪声σ<1.5时,由于噪声误差较小,星点落到错误栅格内的概率较低，改进栅格算法的优势并没有显现出来，两种识别算法的识别成功率相差不大；当星点位置噪声σ>1.5时，星点落到错误栅格内的概率增加，原有栅格算法反映不出特征模式间的相似程度，影响了识别成功率。而改进的栅格算法能很好地反映出特征向量的相似程度，对位置误差有很强的鲁棒性，当星点位置噪声σ=2.5时,也能达到94 %的正确率。从仿真结果可以看出，改进的栅格算法相比于原有的栅格算法对位置噪声具有更好的鲁棒性。

图7为位置噪声σ=0.5像素、星等噪声为σ=0.2星等时，两种算法的星图识别成功率随着“假星”数变化的曲线。

图7 识别成功率随“假星”个数的变化曲线

从图7 可以看出，本文改进后栅格算法对“假星”同样具有很好的鲁棒性，而且在同等条件下，改进后的栅格算法比原有的算法具有更高的识别成功率。

4 结 论

将度量函数的概念引入到传统的栅格算法中，改进算法可以通过特征模式之间的度量函数值的大小来判断其相似度，消除了星点位置噪声对星图识别成功率的影响，提高了改进算法的鲁棒性。仿真结果表明:当星点位置噪声达到一定程度(σ>1.5)或存在“假星”的条件下，改进的栅格算法的星图识别成功率均要高于传统的算法，说明了在鲁棒性和精度方面，改进算法比传统算法有更好的表现。

但由于本文算法引入了度量函数，增加了比较计算环节，增加了计算量，使得改进后的识别算法时间变长。下一步需对改进算法的做进一步优化。

[1] 文 涛,王宏力,陆敬辉,等.基于星三角形外接圆的星图识别算法[J]. 传感器与微系统,2012,31(2):74-76.

[2] 胡 坤,陈嘉鸿,谢元平.一种基于旋转不变特征的星图识别算法[J].光电工程,2015,42(6):20-26.

[3] 孙晓雄,王宏力,陆敬辉.一种基于星三角形的星图识别算法[J].传感器与微系统,2009,28(12):8-10.

[4] Kosik J.Star pattern identification aboard an inertially stabilized spacecraft[J].Journal of Guidance,Control and Dynamics,1991,14(1):230-235.

[5] Udomkesmalee S,Alexander J,Tolivar F.Stochastic star identification[J].Journal of Guidance,Control and Dynamics,1994,17(6):1283-1286.

[6] Padgett C,Kreutz-Delgado K.A grid algorithm for autonomous star identification[J].IEEE Trans on Aerospace and Electronic System,1997,33(1):202-213.

[7] Padgett C,Kreutz-Delgado K,Udomkesmalee S.Evaluation of star identification techniques[J].Journal of Guidance,Control & Dynamics,1997,20(2):259-267.

[8] 张广军.星图识别[M].北京:国防工业出版社,2011:99-100.

[9] Zhang G,Wei X,Jiang J.Full-sky autonomous star identification based on radial and cyclic features of star pattern[J].Image and Vision Computing,2008,26(7):891-897.

[10] 孙 龙.基于星敏感器的捷联惯性/天文组合导航研究[D].哈尔滨：哈尔滨工程大学,2015:41-42.

A modified grid algorithm for star map identification*

QIAN Hua-ming1, LANG Xi-kai1, LI Meng2

(1.College of Automation, Harbin Engineering University,Harbin 150001,China;2.China Aviation Optical-Electrical Technology Co Ltd,Luoyang 471003,China)

Considering that the characteristic pattern extracted by traditional grid algorithm can’t reflect its internal similarity degree,which can affect the accuracy of star map recognition,a modified grid algorithm is proposed.The algorithm uses the metric functions derived from the characteristic patterns to reflect the similarity degree between different characteristic patterns,which solves the problem exists in feature mode extraction because influence of the position measurement error.Simulation environment according to the real situation is set up.The results indicate the star map identification success rate of the proposed method is obviously higher than the traditional algorithm when the star point position error is greater than 1.5 pixels and the improved algorithm of star map recognition success rate is superior to the existing algorithms in the presence of“artificial star”,which shows the validation of the proposed algorithm.

grid algorithm; characteristic pattern; similarity degree; measurement function

2016—06—23

国家自然科学基金资助项目(61573113)

10.13873/J.1000—9787(2017)06—0150—04

V 448

A

1000—9787(2017)06—0150—04

钱华明(1965-)，男，博士，教授，博士生导师，主要从事组合导航、信息处理、传感器技术与智能系统技术工作。

郎希开，通讯作者，E-mail:178708172@qq.com。