基于全质心—Taylor的UWB室内定位算法*
王 磊, 李鹏涛, 贾宗璞
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
基于全质心—Taylor的UWB室内定位算法*
王 磊, 李鹏涛, 贾宗璞
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
针对室内环境下的非视距(NLOS)传播给定位精度造成较大误差的问题,通过对超宽带(UWB)定位模型进行分析,提出了一种基于全质心—Taylor的混合定位算法。采用对测距误差不敏感的全质心算法将锚点测距数据分组运算,获得目标节点的初始粗定位信息,采用质心修正算法对粗定位节点进行优化运算,从而确定Taylor级数展开初值,再进行迭代求解,进行第二次精细定位。实验结果表明:与Chan-Taylor算法、最小二乘估计(LSE)—Taylor算法相比,本文算法定位精度有明显提高。
超宽带; 室内定位; 泰勒算法; 全质心算法; 质心修正算法; 混合定位
0 引 言
随着移动通信和无线传感网络的快速发展,室内环境下基于位置的服务(location-based service,LBS)应用受到越来越多重视。室内定位技术[1]在智能家居、智慧超市、仓库安全存储等方面的应用都需要获得高精度的定位信息,但是室内环境复杂,信号传播很容易受到人员、墙体以及其他障碍物的阻挡产生非视距(non-line-of-sight,NLOS)传播的现象,严重影响定位精度,所以,需要寻找高精度和高鲁棒性的室内定位技术。
现有室内定位技术主要包括无线局域网(wireless area netorks,WLAN)定位,Bluetooth定位,射频识别(RFID)定位和超宽带(ultra wideband,UWB)定位[2,3],其中,UWB技术[4]具有高分辨率、抗多径效应、穿透力强、频谱利用率高、成本低、功耗低的特点,非常适用于高精度的室内定位[5]。
UWB定位技术采用相对带宽大于20 %或者绝对带宽大于500 MHz的ns级窄带脉冲进行通信,具有较高的时间分辨率。利用这一特性,采用基于信号到达时间(time of arrival,TDOA)或者到达时间差(time difference of arrival,TOA)的测距方式,建立锚点与目标点之间距离的非线性方程组,一般采用最小二乘法估计(LSE)[6]、Fang算法[7]、Chan算法[8,9]和Taylor算法[10]对非线性方程组进行求解。LSE法求得的是次优解;Chan算法采用2次最大似然估计,在噪声服从高斯分布的情况下定位精度高,但是在NLOS环境下Chan算法定位精度显著下降;Fang算法为基于TDOA的定位算法,测距过程中如果某个测量值误差很大会导致定位结果出现极大偏差;Taylor算法求解精度高、收敛速度快是求解非线性方程的有效方法,但是Taylor算法对初始值有很强的依赖性,只有通过迭代运算的初始值有一定的准确度才能有较快的收敛速度。
室内环境下NLOS传播大量存在,UWB脉冲信号在NLOS传播时引起附加时延,产生测距误差。因此,本文提出了一种基于全质心—Taylor的UWB定位算法,算法先采用全质心算法[11]将参考节点分组运算获得目标节点的初始粗定位信息,然后通过质心修正算法对初始定位信息进行数据处理,并将处理结果作为Taylor级数展开的初值进行迭代求解,进行第二次精细定位获得高精度的定位结果。
1 方案设计
图1是UWB定位系统原理图。锚点位置信息已知,定位过程中锚点和目标节点之间进行脉冲通信并将测量的TOA信息传送给上位机,由上位机对测量的数据进行处理计算出目标节点的位置坐标。
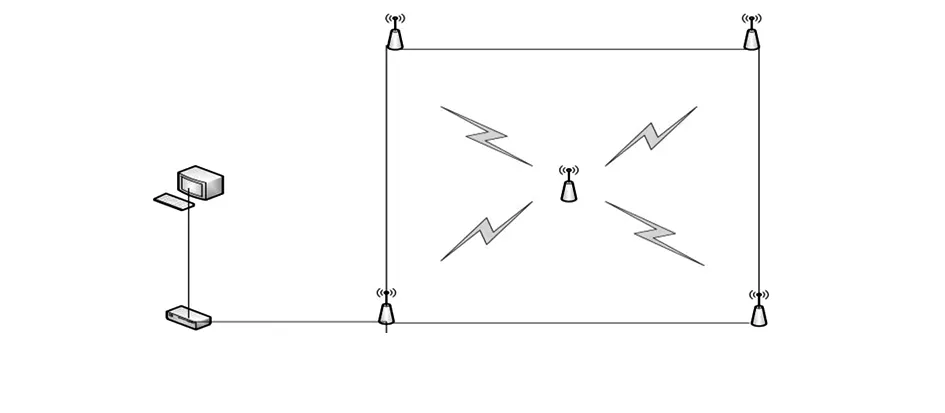
图1 UWB定位系统原理
为解决常规TOA测量方式中收发两端时钟同步的问题,采用来回程的定位方式。原理为锚点先向目标节点发送定位序列,目标节点接收到序列帧以后经过一个固定时延发出响应信号,锚点接收响应信号后根据式(1)计算一次来回程时间(round-trip time,RTT),并根据式(2)求出锚点和目标节点间的距离di如下
tRTT=2tRU+tD
(1)
di=0.5c(tRTT-tD)
(2)
式中tRU为单程到达时间;tD为目标节点转发前的固定时延;c为电磁波在真空中的传播速度。已知锚点坐标为(X1,Y1),(X2,Y2),…,(Xn,Yn),目标节点的坐标为(X0,Y0),根据已知条件可以列出定位方程组,如式(3)所示
(3)
但是室内环境复杂,NLOS传播大量存在,导致TOA测量存在偏差,因此,需要一种高精度的定位算法对定位方程组求解来获得目标节点的坐标信息
2 算法实现
由于单一的定位算法不能满足对室内定位精度越来越高的要求,而混合定位算法可以将不同算法的特征有效结合,在提高定位精度方面有独特的优势,成为室内定位算法研究的主流方向。
2.1 Taylor算法
假设定位目标的真实坐标为(X,Y),通过迭代估计出位置坐标为(X0,Y0),真实坐标和估计坐标关系如式(4)所示
(4)
算法从一个假定的初值坐标(X0,Y0)开始进行迭代运算,将式(3)中的方程进行Taylor展开求出估计坐标与真实坐标的差(ΔX,ΔY)
(5)
式中
A=
(6)
(7)
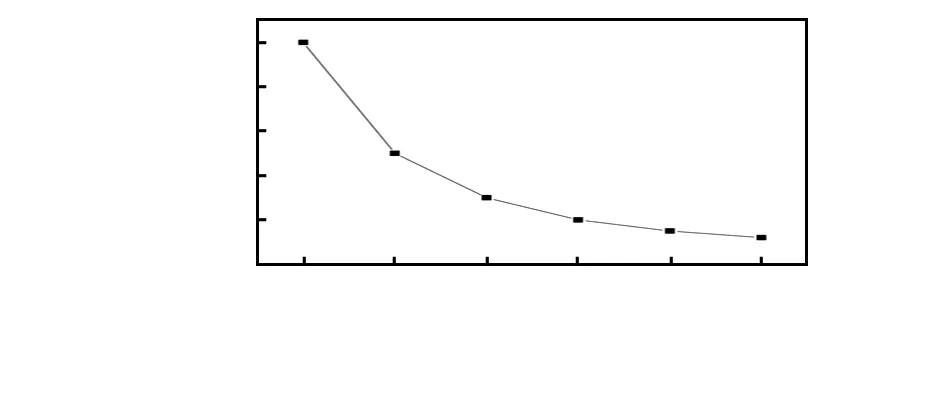
在下一次迭代运算中令X0=X0+ΔX,Y0=Y0+ΔY,直到满足|ΔX|+|ΔY| Taylor算法进行迭代运算求解定位方程可以获得高精度的定位结果,但Taylor初值选取不精确会出现不收敛的问题。一些学者采用最小二乘法[12]、质心算法[13]、Fang算法[14]、Chan算法[15]进行初值的选取。质心算法是一种无须测距的方法定位精度十分有限;Fang算法对运算过程中提取的定位参数要求比较高,在NLOS测距误差比较大的情况下定位精度明显下降;LSE法和Chan算法不仅容易受NLOS环境影响,而且计算量比较大。对Taylor算法来说取得初值越快越好,所以,本文采用全质心算法为Taylor级数展开提供初值,对于NLOS环境对定位误差的影响,采用质心修正的方式减少定位误差。 2.2 全质心算法 定位区间内任何3个不在一条直线上的锚点,都可以用3点定位法,如图2所示已知参考节点A,B,C到定位节点O(xo,yo)的距离为da,db,dc,可以得到式(8) (8) 理想情况下,当采用三边测量时,以A,B,C为圆心,以da,db,dc为半径的3个圆会交于点O,但在应用环境中,由于NLOS的干扰,信号在传输的过程中产生正向误差,使3个圆不能很好地交于一个公共点,如图3所示。 图2 LOS和NLOS下三边测距 非视距误差将导致三边测量时交汇出公共区域,而目标节点位于公共区域内的某一点上,全质心算法是求3个圆所有交点坐标的质心,而且计算出来的解均为实数解,其计算结果具有很高的精度和鲁棒性。将式(8)用矩阵表示 (9) (10) 定义 (11) 则有 Qθ=b (12) 其最小二乘解为 θ=(QTQ)-1QTb (13) 最终求得坐标值(x0,y0)。 2.3 质心修正算法 定位过程中3个锚点可以确定目标节点的二维坐标值,但是NLOS传播时在部分锚点测距误差比较大的情况下,直接采用3点定位的方法精度并不理想,为了提高定位精度设置更多的锚点协同定位,并提出了对锚点分组运算的方法削弱NLOS的影响。 将定位区间内所有锚点以3个为一组(不在同一条直线上)进行分组,得到n组三边测量数据,采用全质心算法分别求出每一组锚点对目标节点的定位坐标值(x1,y1),(x2,y2),…,(xn,yn),每一组测量数据不同求出的定位坐标值偏离真实节点的距离也不相同,为了确保Taylor初值的可靠性,采用质心修正算法对已知的定位节点进行优化处理。首先,求出所有定位坐标值的质心值(x′,y′),如式(14) (14) 直接用质心算法对每组锚点求得目标节点的坐标值求解计算出所有锚点定位初值的质心值,但是部分严重偏离定位节点的定位初值的计算影响定位精度,所以,采用质心修正的方式对求得的质心值进行多次循环优化处理。 1)计算当前定位坐标值(xi,yi)到其质心值(x′,y′)的距离di为 (15) 2)对距离值d1,d2,…,dn从大到小进行排序,找出最大距离值dk对应的定位坐标值(xk,yk),对(xk,yk)以外的其他位坐标值再次质心求解得到质心值(x″,y″)。 3)计算2次质心值(x′,y′),(x″,y″)之间的距离dz,并和设定的阈值p进行比较。 4)当dz 5)当dz>p时,剔除定位坐标值(xk,yk),并从步骤(1)对当前定位坐标值计算直到满足要求。 为了验证算法的有效性,采用DecaWave公司开发的UWB模块DWM1000(图4)对本文算法进行实验验证。DWM1000模块集成了DW1000芯片、石英晶体、天线、无源元件和平衡/不平衡转换器。采用ST公司生产的处理器STM32f103实现系统控制,外接8 MHz晶振实现时钟控制。 图4 DWM1000模块 基于全质心—Taylor的UWB室内定位算法,采用全质心算法作为初步位置计算,采用质心修正算法对初定位结果进行优化处理并为Taylor算法求出Taylor初值的3步定位算法。为了确保定位精度的稳定性,在室内环境中选取6个相距一定距离的位置作为定位节点,在每个位置均实现100次定位计算,求出定位节点的平均定位坐标值并和真实坐标比较,计算其定位误差,即 (16) 式中 (xp,yp)和(xq,yq)分别为目标节点的真实坐标和定位坐标。 图5为在实验室对4个均匀分布的目标节点用3种室内定位算法在相同情况下定位误差的比较。3种室内定位算法均以Taylor展开算法为核心,区别在于对所选取的初始值算法不同,LSE和Chan氏算法没有对测距信息进行筛选,而本文算法采用质心优化算法削减了NLOS对定位精度的影响,从图5可以看出:本文提出的算法和另外2种算法相比定位精度有明显的提高。 图5 3种定位算法比较 当测距误差增加时,定位误差也将增加,定位精度随之降低,为了获得高精度的室内定位,可以通过在定位区域增加锚点数量,引入测距数据冗余来实现。如图6所示,随着锚点数的增加定位精度不断提高,当锚点数目从4个增长到7个时,定位精度有明显提高;当锚点数目从7个到9个定位精度变化趋于缓慢。随着锚点数目的增加,虽然定位精度有显著的提高,但是算法复杂度增加,硬件成本也随着增加,在实际应用中应该根据具体环境确定锚点个数。 图6 不同锚点数下精度变化 针对室内定位过程中存在的NLOS问题,提出了基于全质心—Taylor的UWB室内定位算法。利用UWB技术时间分辨率高的特点,获得参考节点和目标节点的TOA测量值[16],并用全质心算法实现对目标节点的原始粗定位,然后用质心修正算法对粗定位坐标进行优化,并将优化后的值作为Taylor展开的初值,最后采用Taylor算法得到最终的定位结果。仿真结果表明,文中提出的算法和传统的Chan-Taylor算法,LSE-Taylor算法相比明显提高了定位精度。 [1] 洪 雁,王培康.基于稀疏表示多分类的室内定位算法[J].无线电工程,2014,4(2)46-49. [2] 韩下林,赵卫东,季 军,等.基于RFID技术的室内定位算法及其改进[J].计算机工程,2015,34(22):266-267. [3]CetinO,NazhH,GurcanR,etal.AnexperimentalstudyofhighprecisionTOA-basedUWBpositioningsystems[C]∥Proceedingsof2012IEEEInternationalConferenceonultra-wideband(ICUWB),Syracusem,NY:IEEE,2012:357-361. [4] 宋广仪.超宽带高速数据传输技术研究[J].无线电工程,2014,44(5):23-25. [5]DengZhongliang,YuYanpei,YuanXie,etal.Situationanddevelopmenttendencyofindoorpositioning[J].ChinaCommunications,2013,10(3):42-55. [6] 谢胜东,胡爱群,黄 毅,等.基于到达时间差的两步最小二乘定位算法[J].东南大学学报:自然科学版,2013,43(6):1157-1161. [7] 邹 杰,李珊君,陈晓明.一种改进的室内无线定位算法[J].计算机工程,2011,37(14):76-79. [8] 刘春红,陆萍萍.基于Chan氏算法和最近邻居算法的协同定位算法[J].无线通信技术,2012(3):8-15. [9] 杨天池,金 梁,程 娟.一种基于TOA定位的Chan改进算法[J].电子学报,2009,37(4):819-822. [10] 王瑞荣,郑书万,陈浩龙,等.一种基于Taylor和Kalman的室内协同定位方法[J].传感技术学报,2014,27(11):1557-1561. [11] 朱 浩,顾宗海,苏 金,等.一种基于交点质心求解的RSSI定位算法及其优化[J].郑州大学学报:工学版,2010,31(6):43-46. [12] 任 斌,徐会彬.基于总体最小二乘的泰勒级数展开的TOA的UWB定位方法[J].科学技术与工程,2013(21):6129-6133. [13] 张瑞峰,张忠娟,吕辰刚.基于质心—Taylor的UWB室内定位算法研究[J].重庆邮电大学学报:自然科学版,2011,23(6):717-721. [14] 王 彪,傅忠谦.基于超宽带技术的TDOA室内三维定位算法研究[J].微型机与应用,2013,32(14):83-86. [15] 陈德章,唐 皓,吴季达.基于Chan和Taylor的TDOA协同定位算法研究[J].计算机科学,2011,38(10A):406-411. [16] 杨小凤,陈铁军,陈宇宁.基于TOA估计的超宽带快速定位方法[J].现代雷达,2016,38(3):28-31. UWB indoor localization algorithm based on full centroid and Taylor* WANG Lei, LI Peng-tao, JIA Zong-pu (School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China) A novel full centroid and Taylor cooperative positioning algorithm of ultra wideband(UWB)is proposed aiming at problem of big error of localization precision caused by NLOS propagation in indoor environment.The full centroid positioning algorithm that is not sensitive to localization error is used as the initial rough localization by using anchol point ranging data grouping operations,and then Centroid scheme and selecting the rough localization nodes are applied to coarse localization node preliminary optimization,and the optimized value as the Taylor initial value.Simulation results show that this method has superior positioning precision than Chan-Taylor and LSE-Taylor algorithm. ultra wideband(UWB); indoor localization; Taylor algorithm; full centroid algorithm; centroid correction algorithm; cooperative localization 2017—04—14 河南省重点科技攻关资助项目(152102210102);河南省教育厅科技攻关计划资助项目(13A520321);河南省科技厅公关计划资助项目(132102210123) 10.13873/J.1000—9787(2017)06—0146—04 TP 393 A 1000—9787(2017)06—0146—04 王 磊(1977-),男,博士后,副教授,从事物联网,计算机网络技术,E-mail:wang_leiqjy@163.com。 贾宗璞(1963-),男,通讯作者,教授,博士生导师,从事计算机网络技术研究工作。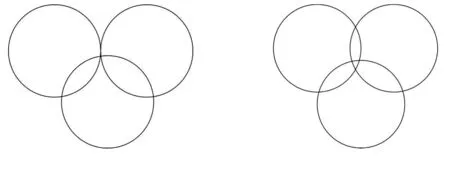
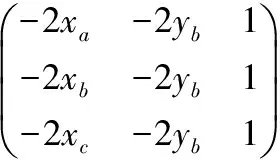

3 实验结果与算法分析

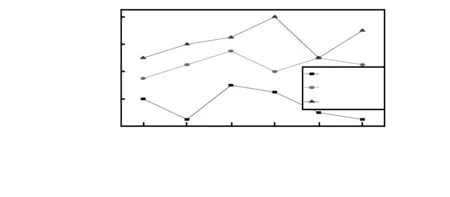
4 结束语

