基于分数阶统一混沌系统的图像加密算法*

毛骁骁， 孙克辉， 刘文浩

(中南大学 物理与电子学院, 湖南 长沙 410083)

基于分数阶统一混沌系统的图像加密算法*

毛骁骁， 孙克辉， 刘文浩

(中南大学 物理与电子学院, 湖南 长沙 410083)

为了解决数字图像信息传输所面临的安全性问题，基于分数阶统一混沌系统，提出了一种新的图像加密算法。采用经典的置乱—扩散机制，整个加密策略分为图像像素位置置乱和像素值替代两个过程。在像素置乱的过程中，采用排序的方式分别对图像的行和列进行置乱。在像素值替代的过程中，通过与密钥序列进行异或运算来实现加密。而混沌系统则作为伪随机序列发生器，并作用于加密的各个阶段。安全性和时间复杂度分析表明：该算法具有高的安全性和低的时间复杂度，且能够抵御几种常见的攻击方式。

分数阶统一混沌系统； 图像加密； 安全性和时间复杂度分析

0 引 言

随着计算机技术和网络技术的发展，信息安全的问题日益凸显[1～3]。然而传统的文本加密算法DES(data encryption standard)和AES(advanced encryption algorithm)并不适用于加密图像，难以满足实时加密的要求[4]。在此背景下，基于混沌的图像加密策略引起了广泛地关注[5～12]。混沌系统具有初值敏感性、遍历性和类噪声性等特点，使其在密码学应用中具有天然的优势，且混沌序列通过简单迭代即可生成，能满足事实性要求。

混沌系统根据系统维数的不同可分为低维混沌系统和高维混沌系统[13]。低维混沌系统具有迭代速度快、硬件实现简单等优点，但因其结构简单以及密钥空间小而存在安全隐患。相反，高维混沌系统具有更复杂的动力学特性和大的密钥空间，因此，安全性更高，但硬件实现相对复杂，且其时间开销相对较大。此外，根据系统阶数的不同，混沌系统可分为整数阶混沌系统和分数阶混沌系统。相比于整数阶混沌系统，分数阶混沌系统已被证明具有更大的密钥空间和更复杂的随机序列，因而具有更好的安全性，且被广泛地应用于数字信号处理、保密通信和数字水印等领域[14～16]。但目前基于分数阶混沌系统的图像加密算法研究仍然较少[17]。因此，基于分数阶混沌系统的研究具有重要的现实意义和广泛的应用价值。

但是分数阶混沌系统在应用于图像加密时也存在时间开销较大的不足。针对这一问题，一方面选用Adomian分解算法[18]来求解分数阶系统。相比于频域算法和预估—校正算法，Adomian分解算法因速度更快，所占系统内存资源更少，而被广泛地应用。另一方面，优化加密算法设计，尽量减少系统的迭代开销，从而获得低的时间复杂度。

本文基于分数阶统一混沌系统来设计图像加密算法，提出了基于Adomian安全性和时间安全性分析表明，该算法具有高安全性和低时间复杂度，且能抵制几种常见攻击方式。最后得出了结论。

1 分数阶统一混沌系统设计

分数阶统一混沌系统方程为[19]

(1)

式中 α为系统参数，q为系统的微分阶数。这里采用速度较快的Adomian分解算法[18]来求解。取参数α=1，q=0.90时，其Lyapunov指数为(3.198 1,0,-20.026 9)，系统为混沌态。此时，系统的吸引子相图如图1所示。

图1 分数阶统一混沌系统的吸引子相图

2 混沌图像加密算法设计

设计的图像加密算法的流程图如图2所示。可见，整个加密算法可分为图像像素位置置乱和像素值替代两个过程。首先，通过行列双方向排序的方法实现图像像素的位置置乱。之后，通过行列像素替代操作实现图像像素值的替代。而分数阶统一混沌系统用于生成伪随机序列，并作用于加密的各个阶段。加密算法的具体步骤如图2所示。

图2 加密算法流程图

2.1 图像位置置乱过程

(2)

(3)

2)生成位置置乱序列IX，IY:令L=max(M,N)。迭代统一混沌系统m+L(m=1 000)次并舍弃前m个值，以消除暂态效应，增强初值敏感性，得到3个混沌序列如下

X={x1,x2,…,xL}

(4)

Y={y1,y2,…,yL}

(5)

Z={z1,z2,…,zL}

(6)

根据式(7)和式(8)按升序对序列X(1∶M)，Y(1∶N)进行排序

[A,IX]=sort(X)

(7)

[B,IY]=sort(Y)

(8)

式中 A，B为排序后的新序列，IX为A中每一项对应X中项的索引，且IY为B中每一项对应Y中项的索引，分别为

IX={r1,r2,…,rM}

(9)

IY={c1,c2,…,cN}

(10)

3)行位置置乱:记行位置置乱后的图像为T1，则通过式(11)实现对原始图像P的每一行所在位置进行置乱

T1(i,:)=P(ri,:),i=1,2,…,M

(11)

式中 P(i,:)为第i行像素。

4)列位置置乱:记列位置置乱后的图像为T，则通过式(12)实现对行置乱图像T1的每一列所在位置进行置乱

T(:,j)=T1(:,cj)，j=1,2,…,N

(12)

经过以上步骤，置乱过程结束，得到置乱后的图像T。

2.2 图像像素替代过程

1)生成加密密钥:令α=1，q=0.9，取混沌系统的初始条件为(x0,y0,z0)=(1,5,20)，迭代统一混沌系统m+L次并舍弃前m个值，以消除暂态效应，增强初值敏感性，得到三个新的混沌序列如下所示

(13)

(14)

(15)

接着通过式(16)和式(17)生成取值范围为[0,255]的加密密钥序列k1，k2如下

(16)

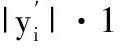
(17)

2)行像素替代:输入位置置乱后的图像T。通过式(18)对T的每一行像素与密钥k1进行异或运算，得到行加密后的图像C为

(18)

式中 c0为外部引入参数，可取[0,255]内的任意整数。

3)列像素替代:通过式(19)对C的每一列像素与密钥k2进行异或运算，得到列加密后的图像D作为最终的加密结果。解密是加密的逆过程

(19)

3 仿真结果

加解密实验的仿真环境为Matlab 8.0，仿真结果如图3所示。原始图像选用256×256的灰度图像Lena。

图3 加解密结果

4 算法安全性和时间复杂度分析

4.1 密钥空间

一个理想的图像加密算法应该有足够大的密钥空间来抵御穷举攻击。在本密码算法中，加密密钥包括统一混沌系统的初始条件(x0,y0,z0)和系统参数α。假设计算精度达到10-15时，系统的密钥空间为1015×1015×1015×1015=1060≈2200。根据目前计算机的计算能力，可知该密码系统足以抵御穷举空间。

4.2 密钥敏感性分析

一个好的密码系统除了应该有足够大的密钥空间外，还应该对其密钥足够敏感。这意味着如果加密或者解密密钥微小的改变将使得加密或者解密的结果完全不同。在测试中，分别采用4个微小偏差的密钥x0+10-15,y0+10-15,z0+10-14,α+10-15去解密加密的Lena图像，如图3(c)，解密结果如图4所示。可见，解密结果与正确解密的Lena图像，如图3(d)完全不同。因此，该密码算法对密钥极其敏感。

图4 错误解密结果

4.3 分布直方图

对于一个良好的图像加密算法，其加密图像的分布直方图应该尽可能的平坦。图5显示了原始Lena图像及其加密图像的直方图。可见，原始图像的像素分布不均匀，而加密图像的分布较为平坦。因此，具有较好的抗统计攻击的能力。

图5 分布直方图

4.4 互相关系数

原始图像的相邻像素具有较高的相关性，而加密算法的目标之一就是打破这种相关性。这种相关性可以通过相邻像素对的互相关系数来衡量，且对于理想的加密算法，其加密图像的相邻像素对的互相关系数应该接近于0。相邻像素的互相关系数定义如下

(20)

cov(x,y)=E[x-E(x)] [x-E(y)]

(21)

(22)

(23)

式中 n为像素点数;E(x)和D(x)分别为x的平均值和方差。表1列出了原始图像和加密图像在水平、垂直和对角3个方向上的互相关系数。可知，原始图像的互相关系数接近于1，而加密图像接近于0，从数值上证明了该算法具有较好的抵御统计攻击的能力。

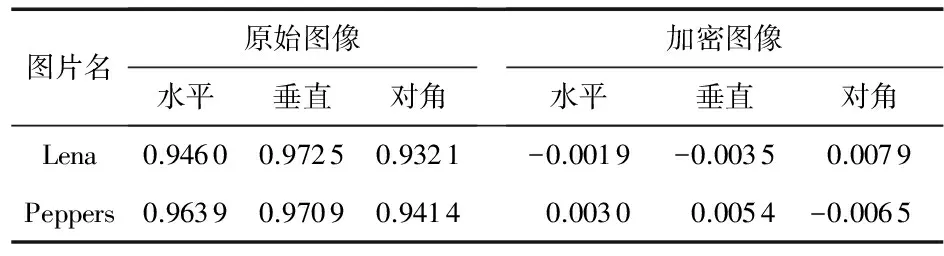
表1 原始图像和加密图像相邻像素对的互相关系数

4.5 抗差分攻击能力分析

差分攻击是一种常用的密码攻击手段。为了获得抵御差分攻击的能力，加密算法必须对明文图像足够敏感，也就是说，明文图像像素值的微小改变，将使得加密结果完全不同。明文敏感性的测试指标包括像素的改变比率(number of pixels change rate,NPCR)和像素值平均改变程度(unified average changing intensity,UACI)。分别定义为

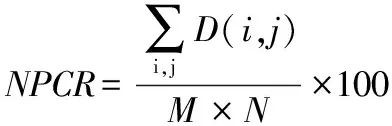
(24)

(25)

式中 M和N分别为原始图像的宽和高；C1(i, j)为加密图像在点(i,j)处的灰度值，C2(i,j)为新的加密图像在点(i,j)处的灰度值，且它们的原始图像仅有一个像素点不同；D(i,j)定义为

(26)

执行100组实验，所得NPCR和UACI的最大值、最小值以及平均值如表2所示。可见平均NPCR大于99.6 %，平均UACI大于33 %，接近于理想值。因此，该算法具有良好的抵御差分攻击的能力。

表2 NPCR和UACI的计算结果

4.6 时间复杂度分析

加密算法的时间复杂度分析是加密性能的一个重要指标。实验环境是2.7 GHz Pentium双核处理器，1.94 GB RAM以及Windows 7操作系统。针对不同256×256的明文图像，一轮加密算法的执行时间如表3所示。可见该算法具有低的时间复杂度。分析可知:对于M×N的图像，在位置置乱和像素值替代的过程中，混沌系统都只需Θ(max(M,N))次迭代耗时操作。因此，在整个加密过程中所需的系统迭代耗时操作较少，从而解决了以往基于分数阶混沌系统的图像加密算法时间复杂度较低的缺点。

表3 一轮图像加密算法的执行时间 s

5 结 论

本文基于分数阶统一混沌系统，采用置乱—扩散机制，提出了一种新的图像加密算法。在该算法中，通过行列双方向排序来置乱图像的像素位置，通过与密钥序列进行异或运算来实现像素值的替代。仿真结果以及算法安全性和时间复杂度分析表明:该算法具有好的加密效果，大的密钥空间，强的密钥敏感性以及低的时间复杂度，且能够抵御差分、穷举、统计等攻击。因此，在数字信息加密中具有良好的应用前景。

[1] 柴秀丽,李 伟,史春晓,等.基于超混沌系统的彩色图像加密新算法[J].传感器与微系统,2013,32(8):131-138.

[2] 艾星星,孙克辉,贺少波,等.简化Lorenz多涡卷混沌吸引子的设计与应用[J].物理学报,2014,63(12):120511.

[3] 朱从旭,孙克辉.对一类超混沌图像加密算法的密码分析与改进[J].物理学报,2012,61(12):1-12.

[4] Hua Zhongyun,Zhou Yicong,Pun Chiman,et al.2D Sine Logistic modulation map for image encryption[J].Information Sciences,2014,297:80-94.

[5] Majid K.A novel image encryption scheme based on multiple chaotic S-boxes[J].Nonlinear Dynamics,2015,82:527-533.

[6] Wang Xingyuan,Wang Qian.A novel image encryption algorithm based on dynamic S-box constructed by chaos[J].Nonlinear Dynamics,2014,75:567-576.

[7] Zhang Wei,Yu Hai,Zhu Zhiliang.Color image encryption based on paired interpermuting planes[J].Optics Communications,2015,338:199-208.

[8] Ye Ruisong.A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism[J].Optics Communications,2011,284:5290-5298.

[9] Majid K.A novel image encryption scheme based on multiple chaotic S-boxes[J].Nonlinear Dynamics,2015,82:527-533.

[10] 孙克辉.混沌保密通信原理与技术[M].北京:清华大学出版社,2015.

[11] 李正周,丁 浩,刘 梅,等.实测海杂波光电图像混沌特性研究[J].传感器与微系统,2013,32(4):27-33.

[12] 刘叙含,申晓红,姚海洋,等.基于帐篷混沌映射观测矩阵的图像压缩感知[J].传感器与微系统,2014,33(9):26-31.

[13] Liu Wenhao,Sun Kehui,Zhu Congxu.A fast image encryption algorithm based on chaotic map[J].Optics and Lasers in Enginee-ring,2016,84:26-36.

[14] Wu Xiangjun,Lu Yang.Generalized projective synchronization of the fractional-order Chen hyperchaotic system[J].Nonlinear Dynamics,2009,57(1-2):25-35.

[15] Kia Arman K,Naser F,Henry P L.A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter[J].Communications in Nonlinear Science & Numerical Simulation,2009,14(3):863-879.

[16] Wang Yaqing,Zhou Shangbo.Image encryption algorithm based on fractional-order Chen chaotic system[J].Journal of Computer Applications,2013,33(4):1043-1046.

[17] 王 力，吕秀宾.基于IBE加密算法的远程抄表系统的优化[J].无线电通信技术，2016,42(1)：86-88.

[18] Zhao Jianfeng,Wang Shuying,Chang Yingxiang,et al.A novel image encryption scheme based on an improper fractional-order chaotic system[J].Nonlinear Dynamics,2015,80:1721-1729.

[19] 贺少波,孙克辉,王会海.分数阶混沌系统的Adomian分解法求解及其复杂性分析[J].物理学报,2014,63(3):030502.

[20] Lü Jinhu,Chen Guanrong,Chen Daizhan,et al.Bridge the gap between the Lorenz system and Chen system[J].International Journal of Bifucation and Chaos,2002,12(12):2917-2976.

孙克辉 (1968-), 男, 通讯作者，教授, 博士生导师，从事混沌保密通信、智能仪器仪表工作，E—mail：kehui@csu.edu.cn。

Image encryption algorithm based on fractional order unified chaotic system*

MAO Xiao-xiao, SUN Ke-hui, LIU Wen-hao

(School of Physics and Electronics,Central South University,Changsha 410083,China)

In order to solve the security problem during transmitting digital image information,a novel image encryption algorithm based on fractional order unified chaotic system is proposed.This algorithm utilizes the classical confusion and diffusion mechanism,and the whole encryption strategy can be divided into two stages:image pixel position permutation and pixel value substitution.In the first stage,each row and column of the image are respectively scrambled by the way of ranking.In the second stage,the pixel values of image are substituted by the XOR operation with key sequence.Besides,the chaotic system is used as pseudo-random sequence generator,and acts on the two stages.Security and time complexity analysis shows that the algorithm has high security and low time complexity,and can resist several common cryptogram attacks.

fractional order unified chaotic system; image encryption; security and time complexity analysis

2016—06—06

国家自然科学基金资助项目(61161006)；中南大学研究生创新基金资助项目(2016ZZTS230)

10.13873/J.1000—9787(2017)06—0138—04

TN 918.4

A

1000—9787(2017)06—0138—04

毛骁骁 (1990-), 男,硕士研究生，研究方向为混沌保密通信。