匀质半球面和半球体质心位置的一种巧解

苟诗涵 李忠相

(重庆市第一中学校,重庆 400030)



匀质半球面和半球体质心位置的一种巧解

苟诗涵 李忠相

(重庆市第一中学校,重庆 400030)

本文介绍一种回避积分求解匀质半球面和半球体质心位置的方法,主要运用了祖暅原理、自相似法、公式法和负质量法等．

质心的求解; 祖暅原理; 自相似法; 负质量法

在学校组织的一个物理系列讲座中老师介绍了物体质心位置的一些常见求解方法,例如公式法、负质量法、自相似法以及巴甫斯定理等．作为示例,求解了匀质半圆环、匀质半圆板等物体的质心位置,最后老师给出了一道拓展思考题:求解匀质半球面和半球体的质心位置．

经过初步的思考,笔者发现这的确是一道难题．于是用了4天时间,从不同的角度进行思考,在基本方法和这个问题间建立联系,最终通过4步转化或分解,终于将这个问题解决了,具体方案如下．

第1步,用祖暅原理转化问题.

祖暅,中国南北朝时期的数学家、天文学家,祖冲之之子．他提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的祖暅原理．他由这个原理,成功地得到了球的体积公式．

这里,仿照祖暅的方法将问题转化．图1甲中为一个半径为R的半球体,乙图是底面半径为R、高也为R的圆柱再挖去一个底面半径为R,高也为R的圆锥之后的形状．

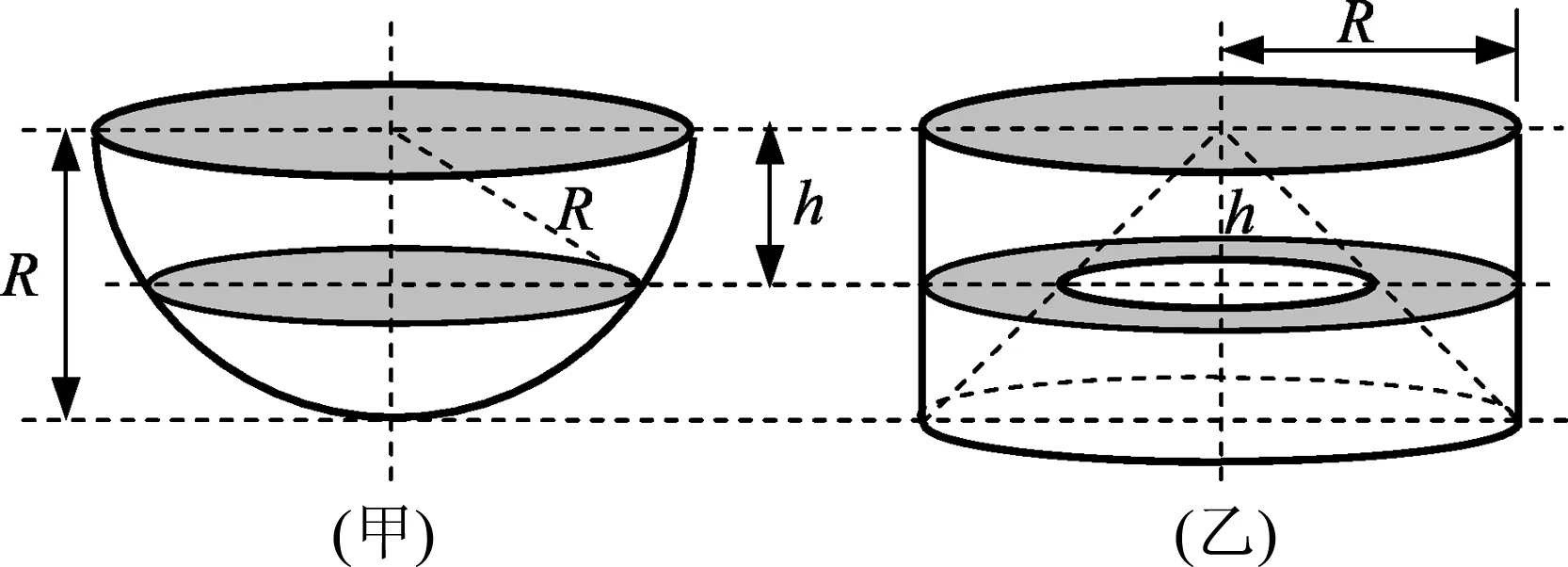
图1 祖暅原理示意图

不难得到,在甲、乙两图中,距离顶面任意高度h处的水平截面(图中阴影部分)的面积都一样,均为

Sh=π(R2-h2).

(1)

不难判断,左右两种形状的质心一定在同一高度处．对于右侧形状,圆柱的质心位置是显然的,只需要进一步求解圆锥的质心位置,即可找到整体质心的位置．

第2步,用自相似法求解匀质圆锥质心.

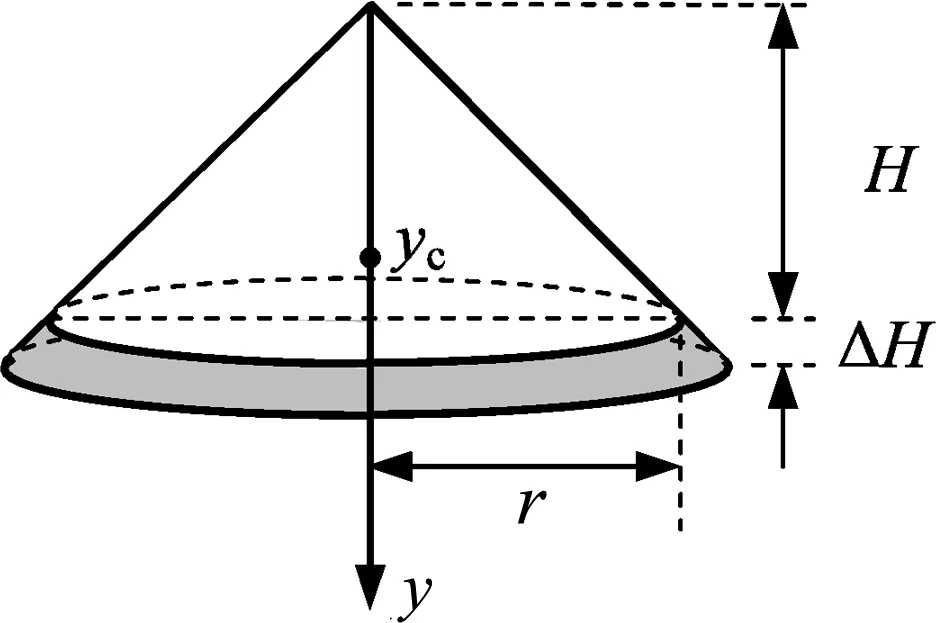
图2

如图2所示,考虑一个高为H、底面半径为r的匀质圆锥,建立以顶点为原点、竖直向下为正方向的y轴,记其质心的坐标为yc．若在圆锥底面以下再继续填充一密度相同的薄层,让其形成一个高为H+ΔH、顶角不变的新圆锥．

新圆锥的质心位置可以由公式法给出(由于新增部分的厚度极小,可将其视为高度极小的圆柱,其质心的坐标可仍记为H)，即

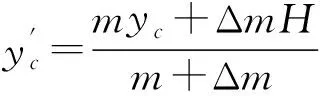
(2)

式中m和Δm分别为原圆锥和新增部分的质量,容易得

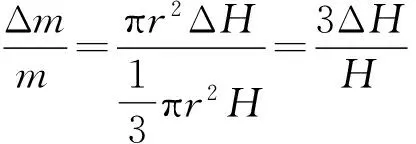
(3)

另一方面,新圆锥又可视为由原圆锥等比例放大的结果,所以新圆锥的质心位置又可记为

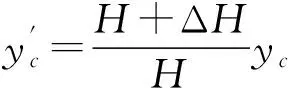
(4)

联立以上几式,可得

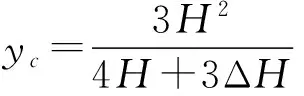
(5)

考虑到ΔH极小,

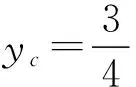
(6)

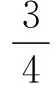
第3步,用负质量法求解匀质半球体质心.

图1乙图,可视为实心圆柱与负质量圆锥的叠加,再利用公式法,可求该系统的质心,即

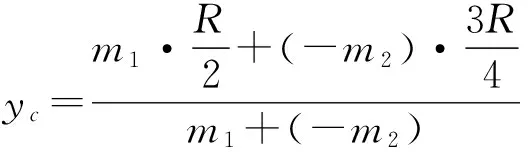
(7)

式中m1和m2分别为整个圆柱和内挖圆锥部分的质量．有

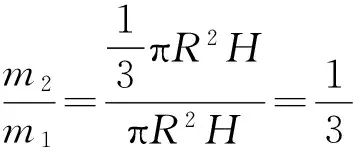
(8)

代入(7)式,即得

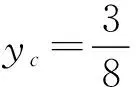
(9)

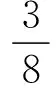
第4步,仿照祖暅原理求解匀质半球面质心.

图3(甲)中为一个半径为R的匀质半球面,右边是底面半径为R、高也为R的匀质柱形圆筒．

在图3(甲)图中,从角度θ到θ+Δθ(Δθ极小)对应的环带,其周长可视为2πRcosθ,宽度为RΔθ,它的面积为

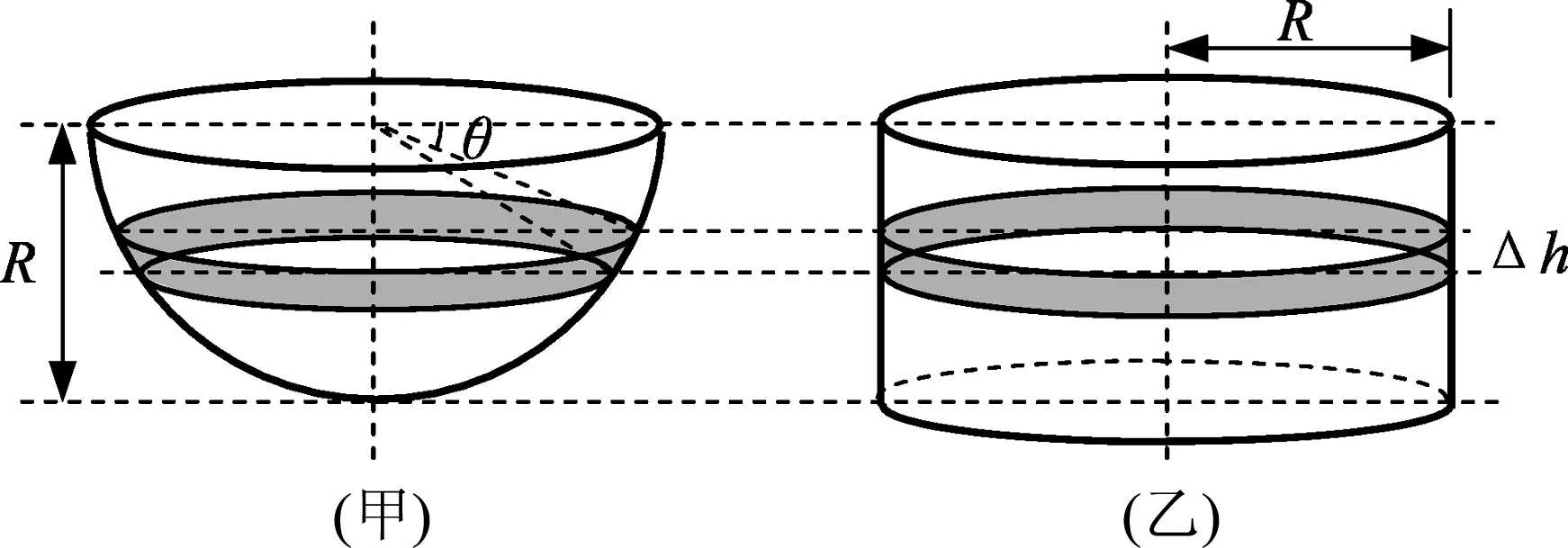
图3 仿照祖暅原理转化半球面

ΔS1=2πRcosθ·RΔθ.

(10)

在图3(乙)图中,总能找到一个与上述环带处在同一水平高度处的环带,其周长为2πR,宽度为甲图中环带宽度在竖直方向的投影,即

Δh=RΔθ·cosθ.

(11)

于是,易得乙图中对应环带的面积为

ΔS2=2πR·RΔθcosθ.

(12)

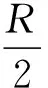
1 栾丽，李忠相.构造相似系统 巧解物理难题[J].物理教学,2016,37(1):48-49.

2016-12-08)