在小学低段教学中也应注意渗透数学思想———以“有几瓶牛奶”为例

◇蒋秀华

在小学低段教学中也应注意渗透数学思想
———以“有几瓶牛奶”为例

◇蒋秀华

“有几瓶牛奶”（北师大版教材一年级上册）主要内容是“9加几”，是进位加法的起始课，也是后续学习的基础。在本节内容中，教材安排了比较长的篇幅，引导学生从不同角度探索计算的方法和“凑十”的策略，结合具体的情境，在解决实际问题的过程中探索“9加几”的进位加法的计算方法，体会转化思想和函数思想，并养成认真仔细的良好习惯。

教学片段一：探索“9加几”的算法

出示教材主题图（如图1），让学生阅读情境图，寻找数学信息，并尝试提出数学问题。

图1

师：现在我们一起解决下面这一个问题：“一共有几瓶牛奶？”

生：（齐）9+5=14。

（板书：9+5=14）

师：你确定等于14吗？大家都同意吗？（生：同意）学数学是要讲道理的，14是怎么来的？请你安静地想一想，过一会儿把你的方法说给大家听。

学生独立思考，在练习本上画一画，或用小棒摆一摆，四人小组交流后进行全班交流。需要说明的是，此时只要学生能口头表达就行，并不要求列出每一步的算式。方法整理如下：

方法1：因为10+5=15，5不变，9比10少1，所以9+5=14。

方法2：因为10+5=15，9+5等于15减1，所以9+5=14。

方法3：5可以分成1和4，先把1跟9相加得10，再加上4等于14。

方法4：5+5=10，9先拿5出来，剩下4，然后用10+4=14。

师：同学们，你们的方法都正确。想一想，你们在算的时候都用到了哪个数？

生：我发现都用到了10。

师：是啊！10是我们的好朋友。用方法1和方法2计算的同学，是把9+5转化成了10+5来算；用方法3和方法4计算的同学，是把9+5转化成了10+4来算。能够把新的题目变成已经学过的知识来做，真是了不起。

思考：在学生想办法来说明9+5为什么等于14的时候，他们用了多种方法。当方法一一列出来后，我们会发现这4种方法看似不同，但其本质是一样的，都是转化成10加几。如何让学生体会到这一点？我以“10”为切入点，只说“把新的题目变成已经学过的知识来做”。我想，在一年级教学中渗透数学思想，并不是把概念说出来，而是渗透其中。

教学片段二：体会“凑十”法

师：我们来观察一下方法3和方法4，你能列出算式吗？

学生尝试列出算式，并组织全班交流。

生1：方法3是9+1=10，10+4=14。

生2：方法3还可以列出9+1+4=14。

生3：方法4是5+5=10，10+4=14，也就是5+ 5+4=14。

师：想一想，这两种方法一样的地方是什么？

生：我发现都是先算出10，再加上4就可以了。

师：试着在计数器上拨一拨，并说说自己的想法。

生1：我先在个位上拨出9颗珠子，表示左边盒子中的9瓶牛奶。再拨出5颗珠子，表示右边盒子中的5瓶牛奶。但是个位上的珠子不够了，因为再拨1颗就是10颗珠子了，我就在十位上拨1颗珠子表示十，个位上放4颗珠子就是14了。

随着学生的表达教师利用课件动态演示 （如图2），并再次共同拨计数器，帮助学生理解“满十进一”。

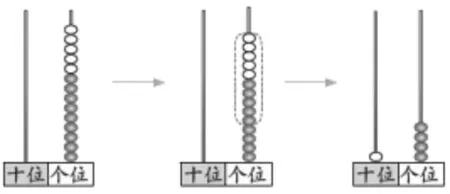
图2

师：大家理解得特别好，其实这两种方法我们通常叫作“凑十”法，你觉得这种方法怎么样？

生：凑成十后就好算了。

生：我觉得稍微有点难，我还要在纸上画一画，才能明白。

师：有困难的同学，可以画一画，也可以数一数手指头来解决问题。

师：我们再来理解一下这种方法，请大家完成下面的题目（如图3）。

图3

学生自主完成题目，并组织全班交流，再次理解“凑十”法。

思考：我认为，“凑十”法应该是本节课每个学生都需要掌握的计算方法，我选择在课堂上单独进行学习，并借助课本上的练习加以运用。但在实际教学中，我发现部分学生理解“凑十”法有一定的困难，所以允许学生画一画，或者数一数小棒、手指头来解决问题，慢慢理解“凑十”法。

教学片段三：拓展练习中体会有序

出示9+□=1□，请学生尝试有序填写。

学生交流，教师板书，并把算式有序地排列如下：

9+1=10

9+2=11

……

师：这些算式，好像是有规律的？你发现了吗？谁来说说你的发现？

生1：我发现第一个加数都是9，第二个加数越来越大。

生2：我发现第二个加数是从小到大，从1开始到9。

师：对，从上往下看，第二个加数每次多1。

生3：我还发现，它们的得数都是十几。

生4：从上往下看，得数也是每次多1，从 10开始，一直到18。

师：同学们观察得很仔细，能不能把刚才几位同学的想法连起来说一说？

生5：第一个加数都是9，从上往下看，第二个加数从小到大，得数也从小到大。

生6：第一个加数不变，从上往下看，第二个加数越来越大，得数也越来越大，而且都是十几。

师：说得很清楚，第一个加数9不变，第二个加数变大，得数也跟着变大。

思考：对函数的定义我们都不陌生：在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应，那么就称y是x的函数。在小学的教材中，我们不难发现一些渗透数学思想的内容和习题，如果能引导学生运用数学思想来发现题目中共同的地方、变化的地方和不变的规律，是一件很有趣的事情。比如，上面这道题9+□=1□，原本只是一道简单的填空计算题，如果用心思考，就会发现其中蕴含的函数思想：a+x=y，在加法算式里，一个加数（a）不变，和（y）随着另一个加数（x）的变化而变化。在适当问题的引导下，学生有能力发现其中变与不变的规律。

（作者单位：广东深圳市福田区侨香外国语学校）