半疏水-半亲水球体垂直入水空泡数值仿真研究

孙钊， 曹伟， 王聪， 路中磊

(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)



半疏水-半亲水球体垂直入水空泡数值仿真研究

孙钊， 曹伟， 王聪， 路中磊

(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)

采用流体体积多相流模型耦合连续表面力模型，对具有非对称表面润湿性的半疏水- 半亲水球体垂直入水空泡形态发展过程进行数值仿真，分析了半疏水- 半亲水球体垂直入水过程中受到的流体动力。研究结果表明：半疏水-半亲水球体垂直入水后，产生非对称入水空泡及“心”型喷溅，同时球体运动轨迹将偏离原竖直运动轨道，由疏水半球一侧向亲水半球一侧偏斜；入水初期，在球体表面形成液体薄层运动，在疏水半球一侧，液体薄层与球体表面分离，导致空气进入形成敞开空泡；在亲水半球体一侧，液体薄层沿球体表面向上运动最终在球体顶点汇聚；液体薄层汇聚后形成楔形流，楔形流在球体顶点与球体表面分离，继续向疏水半球一侧产生的入水空泡壁面运动并撞击，形成“心”型喷溅。

流体力学； 多相流； 半疏水- 半亲水球体； 垂直入水； 表面润湿性； 数值仿真； 空泡

0 引言

入水问题是一个非常复杂的涉及跨介质的固体及液体相互作用问题[1-2]，在运动体入水过程中伴随许多现象，例如撞击瞬间、喷溅现象、入水空泡产生、空泡掐断、空泡溃灭等。许多工程问题及自然现象与入水问题存在重要关系，例如跳弹[3]、空投鱼雷[4]、水上飞机水上着陆[5]、水上行走生物[6]等．

近年来，随着高速摄像以及高速粒子成像技术的发展，研究者们开展了大量有关入水问题的实验研究，例如Dulax等[7]、Grumstrup等[8]、Bergmann等[9]、Aristoff等[10]、Truscott等[11-12]、Techet等[13]、Sudo等[14]。Yilmaz等[15-16]通过粒子图像测速(PIV)技术对球体垂直入水过程展开了实验研究，获得了球体入水过程空泡形态发展规律，并发现入水空泡闭合位置、闭合时间与弗劳德数Fr呈线性关系。Marston等[17]通过高速摄像技术拍摄了球体垂直入水过程在自由液面上方产生的喷溅，观察到了喷溅轮廓的褶皱条纹，并提出了喷溅穹顶的曲率不稳定性。Benedict等[18]通过实验研究了刚性球体垂直进入双层液体的入水空泡现象，该双层液体由不互溶的两种液体组成。这种入水空泡，其空泡壁面不再保持光顺，而是出现波纹状涟漪，且空泡闭合时间、闭合深度与球体垂直落入均一纯水中的入水空泡显著不同。

入水物体的表面润湿性同样对入水空泡有显著影响。路中磊等[19]开展了圆柱空心壳体的低速垂直入水过程，实验结果呈现了波动状态的入水空泡轮廓，入水速度以及空腔壳体几何结构对该波动现象有较大影响。Duez等[20]研究了不同表面润湿性球体的垂直入水空泡，发现只有在入水速度超过某一临界值的情况下才会产生入水空泡，该临界值与球体的表面润湿性有重要关系。Do-Quang等[21]通过耦合Navier-Stokes方程以及Cahn-Hilliard方程方法，利用数值仿真方法研究了不同表面润湿性球体的垂直入水运动，获得了大量的入水空泡矢量场图片。Kintea等[22]通过数值仿真方法研究了旋转刚性球体以及非旋转刚性球体的入水过程，数值仿真方法建立在流体体积(VOF)多相流模型基础上，引入表面张力以及接触角，且数值结果与实验结果吻合良好。

本文通过数值方法研究半疏水- 半亲水球体的垂直入水空泡发展过程。所谓半疏水- 半亲水球体，即球体两侧表面润湿性不对称，一侧半球表面为疏水性表面，另一侧为亲水性表面。一般情况下，球体以一定速度垂直撞击自由液面后，将形成典型的“沙漏状”入水空泡及“皇冠状”喷溅。然而，当球体的表面润湿性不对称时，将产生较复杂的入水现象，例如非对称入水空泡以及心型喷溅，这正是本文的研究重点。

1 数值方法

1.1 控制方程

本文所研究的垂直入水问题，可简化为三维不可压缩二相流问题。数值计算采用VOF多相流模型描述计算流域中气相及液相体积分数，令液相体积分数为α1，则α1=0代表该网格单元没有液相分布；α1=1代表该网格单元全部为液相；0<α1<1代表相界面。对于二相流问题，气相的体积分数即为1-α1.

流动控制方程为

动量守恒方程

(1)

质量守恒方程

(2)式中：ρ为混合物密度；u为速度矢量；μ为混合物动力黏度；p为压强；g为重力加速度；F为表面张力项。

动量方程中的混合物密度ρ以及混合物动力黏度μ由计算流域中各相的体积分数决定：

ρ=ρlαl+ρg(1-αl)，

(3)

μ=μlαl+μg(1-αl)，

(4)

式中：ρl、ρg、μl、μg分别为液相及气相的密度和动力黏度，具体数值如表1所示。

表1 数值过程液相及气相属性Tab.1 Properties of liquid and gas phases in simulation

本文采用Brackbill等[23]提出的连续表面力(CSF)模型，将表面张力项作为源项加入到动量方程中:

(5)

式中：αi、αj分别为i相和j相的体积分数；ρi、ρj分别为i相和j相的密度。

(6)

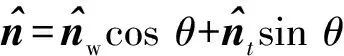
(7)

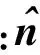
1.2 计算域及网格划分

由于计算域及入水物体在几何结构上具有对称性，为降低计算成本，本文采用1/2模型进行数值计算。

计算域、边界条件以及网格划分如图1所示。D为球体直径，计算域轴向长度40D，自由液面被设置在轴向长度的正中间，即20D处。球体位置设定为刚好接触自由液面前一瞬间的位置，并给予其初始速度u0，计算域整体尺寸为40D×20D×10D. 重力g方向与z轴正向一致，z轴通过球体球心，坐标零点z=0定义为自由液面处，时间零点t=0定义为球体接触自由液面瞬间时刻，数值计算过程以及后续处理选择竖直向下为z轴正向。

图1 计算域、边界条件以及网格划分Fig.1 Computational domain, boundary condition, and mesh generation

全计算域采用结构化网格。球体周围采用O-block网格对球体壁面进行包裹，O-block尺度为4D×4D×2D，并对球体附近网格进行加密，网格划分策略采用BiGeometric，控制比率因子为1.1，如图1(c)所示。

1.3 计算设置

本文应用的数值计算软件为ANSYS Fluent，边界条件设置、计算流域初始化、自编程序的编译等均在软件界面中设置。数值计算过程中，采用VOF法对流动控制方程离散；压力场与速度场的耦合选用压力隐式分裂算子(PISO)算法；压力场的空间离散采用PRESTO！策略；各相体积率离散采用CICSAM策略；各求解变量的离散采用2阶迎风策略；对流项采用QUICK离散策略；相界面的几何重构采用Geo-Reconstruct策略。

2 结果与分析

2.1 数值与实验结果对比

本文通过与文献[12]实验结果对比，验证数值方法的有效性。数值计算过程中入水运动参数设置与实验一致，球体直径D=5.72 cm，球体质量ms=0.17 kg，入水速度u0=1.72 m/s，亲水性球体表面接触角θ=60°，疏水性球体表面接触角θ=120°.

首先，针对计算域几何模型建立了不同网格密度的结构化网格。通过逐渐降低网格单元尺寸，进行网格细化研究：Finer mesh(包含1 538 340网格单元)；Fine mesh(包含987 600网格单元)；Coarse mesh(包含455 670 网格单元)。

图2给出了球体垂直入水过程运动位移及运动速度随时间变化。如图2所示，随网格数量增加，运动位移及速度差别逐渐减小。拟选定Finer mesh作为本文数值计算网格。在此情况下，数值计算在一个20核心处理器的服务器上进行，时间步长选取经验性的设置1×10-6，平均每一个入水过程算例需要约48 h. 最终认为Finer mesh可以保证计算精度的同时，所需的计算成本是可以接受的，因此作为本文数值计算的最终网格。

图2 疏水性球体不同网格密度计算结果Fig.2 Numerical results of different mesh densities for hydrophobic sphere

两种不同表面润湿性球体的垂直入水空泡数值仿真结果与实验结果对比分别示于图3及图4中。如图3所示，在这种亲水性球体的垂直入水过程中，球体撞击自由液面后仅有一个垂直向上的溅射流产生。随球体下落，在自由液面以下没有形成入水空泡，球体完全被液体包裹，数值仿真结果与实验结果有较高的吻合度。图4为另一组数值仿真结果与实验结果对比。在这种疏水性球体的入水现象中，入水初期液体在球体表面某一位置分离并形成入水空泡，随后入水空泡在自由液面以下某一深度掐断(深闭合)形成经典的“沙漏状”空泡形态，数值仿真结果与实验结果对应良好。

图3 亲水性球体入水空泡形态数值 仿真结果与实验结果对比Fig.3 Comparison of the numerical and experimental results of cavities created by hydrophilic sphere

图4 疏水性球体入水空泡形态数值仿真 结果与实验结果对比Fig.4 Comparison of the numerical and experimental results of the cavities created by hydrophobic sphere

图3及图4所示的两球体入水过程，其中球体直径、入水速度以及液体属性等外界参数完全一致，仅有球体表面润湿性的差别，却产生了完全不同的入水空泡现象，而本文数值方法实现了这种因表面润湿性不同而产生的入水现象差异，且与实验结果对比良好。

入水空泡闭合现象是入水空泡发展过程的重要过程之一，本文分别提取了数值仿真结果与实验结果的入水空泡参数(见图5)：闭合时间tp，闭合深度hp，闭合位置zp，闭合时刻的空泡开口直径Dp，具体量值如表2所示。

2.2 非对称入水空泡形态

亲水性球体与疏水性球体垂直入水后将产生差异较大的入水空泡形态(见图3和图4)，当球体表面润湿性非对称时，例如一侧半球为亲水性表面，另一侧为疏水性表面，即半疏水- 半亲水球体的垂直入水空泡形态如何？这正是本文的研究重点。

图5 入水空泡闭合时刻坐标示意Fig.5 Coordinate for cavity pinching-off表2 入水空泡闭合参数Tab.2 Pinch-off data of water entry cavity

参数数值仿真值实验值误差/%tp/ms94597531hp/mm85587523zp/mm1716175120Dp/mm1298136348

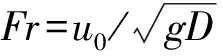
图6 不同表面润湿性球体垂直入水空泡形态Fig.6 Water entry cavities created by spheres with different wettabilities

图6(a)为亲水性球体的入水过程，球体表面接触角θ=60°，俯视图及侧视图均说明该球体在入水过程中没有入水空泡产生。

图6(b)为疏水性球体垂直入水空泡发展过程，球体表面接触角θ=120°，该球体在入水过程中产生了入水空泡，空泡在自由液面下方某一位置掐断，形成典型“沙漏状”入水空泡。

图6(c)为半疏水- 半亲水球体的垂直入水空泡发展过程，该球体左侧半球表面为疏水性表面，θL=120°，右侧半球表面为亲水性表面，θR=60°. 可以预见，在该球体亲水性半球一侧，将呈现类似图6(a)中的无入水空泡现象；而在该球体疏水性半球一侧，将呈现类似图6(b)的入水空泡；最终，将会形成非对称入水空泡。图6(c)示出了这种非对称入水空泡的发展过程，并且从图中可以观察到该球体入水过程中不仅产生非对称空泡，同时球体运动轨迹不再保持竖直向下，而是发生了横向位移。该横向位移方向由疏水侧指向亲水性一侧，即从有空泡产生一侧指向无空泡产生一侧。

值得注意的是，这种半疏水- 半亲水球体垂直入水后不仅产生非对称入水空泡，同时形成“心”型喷溅状态，如图6(c)俯视图所示。疏水性半球一侧排开液体形成敞开入水空泡，亲水性一侧并不产生入水空泡，而是形成液体薄层。液体薄层在球体顶点汇聚后形成尖锐的楔形流，楔形流由亲水半球一侧向疏水半球一侧运动，即图6(c)中从右向左，最终撞击到疏水半球一侧产生的入水空泡壁面。随球体下落，入水空泡及楔形流同时发展形成较明显的“心”型喷溅。

图7为楔形流产生初期入水空泡形态及相应矢量场，空泡壁面在数值后处理过程中被设置为具有一定透明度，因此可以观察到空泡壁面内部的楔形流。图7(a)和图7(c)分别为空泡形态俯视图及侧视图；图7(b)和图7(d)分别为距离自由液面0D、1/2D深度处横断面空泡轮廓及矢量场。如图7所示，楔形流由亲水性一侧产生，在球体顶点位置附近与球体表面分离，并从亲水半球一侧向疏水半球一侧空泡壁面运动，此时楔形流还没有撞击到左侧空泡壁面；从俯视图中可以观察到，由于楔形流的产生，液面上方的喷溅不再呈圆周对称，而是形成“心型”喷溅。

图7 球体入水后t=22.75 ms入水空泡形态及矢量场Fig.7 Cavity formation and velocity field taken for t=22.75 ms after impact

这种楔形流的产生与亲水性一侧球体表面形成的液体薄层有重要关系，如图8所示。对于亲水性球体，产生的液体薄层沿球体表面向上运动，并最终在球体顶部汇合，液体薄层汇合后形成向上的溅射流，不产生入水空泡；对于疏水性球体，液体薄层在运动到球体赤道附近处与球体表面分离，从而导致空气进入并形成入水空泡。半疏水- 半亲水球体由于球体表面的非对称润湿性，液体薄层在两侧球体表面具有不同的运动状态：在亲水性一侧，液体薄层沿表面向上运动，至球体顶点汇聚，形成楔形流尖端，并向左侧继续运动；在疏水性表面一侧，液体薄层极早和球体表面分离，形成开口入水空泡。

图8 不同表面润湿性球体入水初期空泡形态Fig.8 Initial stage of water impact by spheres with different wettabilities

2.3 轨迹、速度、加速度

相对于表面润湿性均一的普通球体，具有非对称表面润湿性的半疏水- 半亲水球体垂直入水后，其最明显以及最让人感兴趣的特征不仅是产生了非对称入水空泡及“心”型喷溅，其运动轨迹也将发生偏斜，如图9所示。

图9 不同表面润湿性球体入水运动轨迹Fig.9 Trajectories of spheres during water entry

非对称入水空泡的产生说明球体两侧与周围水域相互作用的动量传递不对称，导致球体产生水平方向位移(x方向)。球体垂直入水过程是一个球体运动动能及动量与周围流体持续转移变化的过程。随球体下落，球体给每一层水以一个基本上是横向的动量。相应地，流体将反作用力施加于球体本身。

在球体疏水性半球一侧产生入水空泡，说明疏水性半球一侧固体- 液体之间的动量转移比较显著，球体给予周围流体横向动量，相应地，流体传递给球体等值反向的冲量。而在亲水性半球一侧没有入水空泡产生，球体和周围流体几乎不发生动量传递。最终，导致球体两侧受到的流体动力在水平方向上不平衡。因此，球体运动轨迹由疏水性一侧向亲水性一侧偏移，并且入水空泡相应发生一定弯曲，同时产生心型入水喷溅。

图9示出了5种不同表面润湿性球体运动轨迹，球体相对密度ρ*=2.7，入水速度u0=2.37 m/s. 5种不同表面润湿性球体分别为：θ=30°；θL=60°，θR=30°；θL=120°，θR=30°；θL=150°，θR=30°；θ=150°. 球体球心位置的x和z坐标均用球体直径D进行无量纲化，z/D=0代表自由液面。图9中空心三角符号标记了入水空泡闭合时刻球体球心位置。θ=30°和θL=60°，θR=30°两种球体表面两侧均不产生入水空泡，因此不涉及空泡闭合。θ=30°及θ=150°两种球体示出了一条笔直的运动轨迹，其运动方向为竖直向下，入水过程中球体两侧流体流动状态没有发生不对称现象，因此球体运动轨迹没有偏离竖直方向。随球体两侧表面润湿性差异增加，球体运动轨迹偏斜程度越加明显。θL=60°,θR=30°球体运动轨迹仅轻微偏离了竖直方向。θL=120°，θR=30°；θL=150°，θR=30°两种球体，均产生非对称入水空泡，随球体运动轨迹的偏斜，入水空泡也相应发生一定弯曲，并且空泡闭合位置偏离原竖直运动轨道。球体运动轨迹由疏水性一侧向亲水性一侧偏斜，即图9中由左向右，空泡闭合位置也向亲水性一侧偏离原竖直轨道。

为更好地理解不同非对称表面润湿性差异的半疏水- 半亲水球体垂直入水空泡，图10给出了3种不同半疏水- 半亲水球体入水空泡发展过程，运动参数与图9所述一致。3种球体分别为：θL=60°,θR=30°;θL=120°,θR=30°;θL=150°，θR=30°. 如图10(a)所示，对于θL=60°,θR=30°球体，虽然球体两侧表面润湿性不对称，但是垂直入水后球体两侧均不产生入水空泡，因此球体运动轨迹的偏斜并不明显。随半疏水-半亲水球体两侧的非对称表面润湿性差异增加，产生的非对称空泡欲加明显，从而导致球体运动轨迹的偏斜增大，如图10(b)和图10(c)所示。

图10 不同半疏水- 半亲水球体垂直入水空泡形态Fig.10 Water entry cavities created by three asymmetric spheres

2.4 流体动力分析

半疏水- 半亲水球体垂直入水后产生与普通球体完全迥异的入水空泡形态，尤其非对称入水空泡的产生导致球体两侧受到的流体动力不平衡，最终使其运动轨迹偏离竖直运动轨道。本小节讨论非对称润湿表面球体垂直入水过程中的流体动力。首先，给出半疏水- 半亲水球体入水过程位移、速度、加速度随时间的变化，如图11所示。

图11 半疏水- 半亲水球体垂直入水位移、速度以及加速度随时间变化Fig.11 Position, velocity and acceleration in z and x directions as a function of non-dimensional time

图11示出了5种不同表面润湿性球体的位移、速度、加速度随时间的变化，球体密度、入水速度均与图9相同。z/D、x/D分别代表竖直方向位移及水平方向位移；uz/u0、ux/u0分别为竖直方向速度及水平方向速度；az/g、ax/g分别代表竖直方向加速度及水平方向加速度。

如图11(a)所示，θ=30°球体竖直方向位移衰减最小，表明其下落速度最快。随球体整体疏水性增加，z/D衰减越加明显。如图11(b)所示，θ=30°以及θ=150°两种球体由于表面润湿性均一，不产生非对称入水空泡，没有横向位移。θL=60°，θR=30°球体横向位移极小，表明其微弱的横向偏移。θL=150°，θR=30°球体具有最明显的横向位移，说明球体两侧表面润湿性非对称差异越大，横向位移越明显。

图11(c)和图11(d)给出了与图11(a)、图11(b)对应的速度变化。如图11(c)所示，θ=30°球体竖直方向速度衰减相对平缓，随球体表面疏水性增加，速度衰减逐渐增加，θ=150°球体速度uz/u0衰减最大。值得注意的是，拥有疏水性表面的球体，其竖直方向速度在入水空泡闭合期间u0t/D=4～6出现了拐点。通过前面对入水空泡形态发展过程的分析可知，速度出现拐点主要是由于入水空泡深闭合导致球体尾部空泡压强突增，对球体产生一定冲击作用。对于θ=30°及θL=60°，θR=30°两种亲水性表面球体，无论表面润湿性是否对称，球体在下落过程中完全被周围流体包裹，不产生入水空泡，因此不会出现拐点。这种突然加速的过程在图11(e)和图11(f)加速度随时间变化曲线中可以进一步观察到。

轨迹、速度、加速度都包含了重力加速度的作用，为了分析球体在入水过程中受到的流体动力，对球体进行受力分析：球体在入水过程中受到的力为重力mg以及与周围全部的流体(气体及液体)相互作用产生的总流体动力Fh，

(8)

所谓总流体动力Fh，来源于与周围流体相互作用所产生的压力、黏性力、表面张力的综合作用：

(9)

(10)

(11)

式中：u=u(t)为不同时刻的瞬时速度；ρ=ρw=998.2 kg/m3为液体密度；Fhz和Fhx分别为Fh在z和x方向上的分量。

图12给出了不同表面润湿性球体垂直入水过程的总流体动力系数随时间变化。如图12(a)所示，球体触水瞬间，u0t/D=0～0.5时刻，经历几乎相同的入水冲击作用，说明入水冲击作用主要与球体的入水速度有关，和表面润湿性没有显著关系。随后，因不同球体产生的入水空泡发展过程不同，形成一定差异的流体动力。θL=30°，θR=30°和θL=60°，θR=30°两种球体由于不产生入水空泡，在入水初期u0t/D=0.5～2，由于液体薄层沿表面的运动，其流体动力形成一定波动；随后，球体一直处于被周围液体完全包裹的状态，其流体动力趋于恒值。θL=120°，θR=30°和θL=150°，θR=30°两种球体由于液体薄层与球体表面分离，形成入水空泡，在入水初期没有发生类似的波动，而是在空泡深闭合时刻(u0t/D=4～6)出现明显峰值，说明空泡闭合对球体有明显冲击作用。如图12(b)所示，非对称表面润湿性产生的水平方向流体动力先增加后减小，并且在空泡深闭合发生时刻出现峰值，说明非对称空泡的深闭合对球体水平方向的运动同样具有冲击作用。对于非对称差异较小的θL=60°，θR=30°球体，由于球体两侧均不产生空泡，这种水平方向的流体动力微乎其微。

图12 半疏水- 半亲水球体垂直入水流体 动力系数随时间变化Fig.12 Hydrodynamic force coefficients as a function of non-dimensional time

3 结论

本文通过数值方法研究了半疏水- 半亲水球体的垂直入水过程，对非对称入水空泡形态以及入水过程中球体轨迹、速度、加速度、流体动力进行了分析。研究结果表明，通过改变球体表面润湿性，可以有效的改变球体垂直入水现象，尤其可以改变入水空泡形态。

具有非对称润湿表面的半疏水- 半亲水球体，垂直入水后产生非对称入水空泡，说明球体与周围水域相互作用的动量传递不对称，最终导致由疏水半球一侧向亲水半球一侧的横向位移。通过不同半疏水- 半亲水球体的垂直入水过程数值模拟，分析了球体位移、速度、加速度。研究结果表明，这种水平方向的位移和球体两侧的表面润湿性差异有重要关系，对于差异较小的θL=60°，θR=30°球体，横向位移微乎其微；对于差异较大的θL=150°，θR=30°球体，横向位移非常明显，说明非对称润湿性差异越大，产生的非对称入水空泡及轨迹偏转越显著。

半疏水- 半亲水球体的垂直入水运动，展现了具有非对称润湿性表面的运动体入水后更加复杂的入水空泡形态发展过程，进一步说明表面润湿性在入水过程中的重要作用。该方面研究可应用于许多流体动力问题，尤其涉及需要考虑弹道、流体动力、多相流场结构等军事领域及工程应用。在入水运动过程中，考虑表面润湿性的研究目前较少，对于更宽广入水条件的研究，例如更高的入水速度以及更复杂的几何运动体，有待于进一步探索。本文数值仿真方法与相应实验结果吻合良好，在一定程度上奠定了用数值仿真方法研究考虑表面润湿性的入水多相流动过程的可行性。

References)

[1] Worthington A M, Cole R S. Impact with a liquid surface, studied by the aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society of London, 1900, 189:137-148.

[2] Worthington A M. A study of splashes[M]. NY, US: Longmans Green and Company, 1908.

[3] Rosellini L, Hersen F, Clanet C, et al. Skipping stones[J]. Journal of Fluid Mechanics , 2005, 543:137-146.

[4] May A. Water entry and the cavity-running behavior of missiles, ADA020429[R]. Silver Spring, MD, US: NAVSEA Hydroballistics Advisory Committee, 1975.

[5] Von Karman T. The impact on seaplane floats during landing, TN321[R]. Washington DC, US: National Advisory Committee on Aeronautics , 1929.

[6] Bush J W M, Hu D L. Walking on water: biolocomotion at the interface[J]. Annual Review of Fluid Mechanics, 2006, 38: 339-369.

[7] Duclaux V, Caillé F, Duez C,et al. Dynamics of transient cavities[J]. Journal of Fluid Mechanics, 2007, 591: 1-19.

[8] Grumstrup T, Keller J B, Belmonte A. Cavity ripples observed during the impact of solid objects into liquids[J]. Physical Review Letters, 2007, 99(11):114502-1-114502-4.

[9] Bergmann R, van der Meer D, Gekle S,et al. Controlled impact of a disk on a water surface: cavity dynamics[J]. Journal of Fluid Mechanics, 2009, 633:381-409.

[10] Aristoff J M, Truscott T T T, Techet A H, et al. The water entry of decelerating spheres[J]. Physics of Fluids, 2010, 22:032102-1-032102-8.

[11] Truscott T T, Techet A H. A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres[J]. Physics of Fluids, 2009, 21: 121703-1-121703-4.

[12] Truscott T T, Techet A H. Water entry of spinning spheres[J]. Journal of Fluid Mechanics, 2009, 625:135-165.

[13] Techet A H, Truscott T T. Water entry of spinning hydrophobic and hydrophilic spheres[J]. Journal of Fluids and Structures, 2011, 27(5/6):716-726.

[14] Sudo S, Takayanagi H, Kamiyama S. Water entry of a magnetic fluid coated sphere[J]. Journal of Magnetism and Magnetic Materials, 2011, 323(10):1348-1353.

[15] Yilmaz N, Nelson R. Cavity dynamics of smooth sphere and golf ball at low Froude numbers, part 1: high-speed imaging and quantitative measurements[J]. Journal of Visualization, 2015, 18(2): 335-342.

[16] Yilmaz N, Nelson R. Cavity dynamics of smooth sphere and golf ball at low Froude numbers, part 2: PIV analysis[J]. Journal of Visualization, 2015, 18(4): 679-686.

[17] Marston J O, Truscott T T, Speirs N B,et al. Crown sealing and buckling instability during water entry of spheres[J]. Journal of Fluid Mechanics, 2016, 794: 506-529.

[18] Benedict C W T, Vlaskkamp J H A, Denissenko P, et al. Cavity formation in the wake of falling spheres submerging into a stratified two-layer system of immiscible liquids[J]. Journal of Fluid Mechanics, 2016, 790: 33-56.

[19] 路中磊，魏英杰，王聪，等. 基于高速摄像实验的开放腔体圆柱壳入水空泡流动研究[J]. 物理学报，2016,65(1):301-315. LU Zhong-lei, WEI Ying-jie, WANG Cong, et al. An experimental study of water-entry cavitating flows of an end-closed cylindrical shell based on the high-speed[J]. Acta Physica Sinica, 2016,65(1):301-315. (in Chinese)

[20] Duez C, Ybert C, Clanet C, et al. Making a splash with water repellency[J]. Nature Physics, 2007, 3:180-183.

[21] DoQuang M, Amberg G. The splash of a solid sphere impacting on a liquid surface: numerical simulation of the influence of wetting[J]. Physics of Fluids, 2009, 21:022102.

[22] Kintea D M, Breitenbach J, Gurumurthy V T, et al. On the influence of surface tension during the impact of particles on a liquid-gaseous interface[J]. Physics of Fluids, 2016, 28: 012108.

[23] Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J].Journal of Computational Physics, 1992, 100:335-354.

Numerical Investigations on Water-entry Cavity of HalfHydrophobic-half Hydrophilic Sphere

SUN Zhao， CAO Wei， WANG Cong， LU Zhong-lei

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)

The water entry of a solid sphere impacting on a liquid surface has challenged researchers for centuries and remains of interest to the researchers today. A simulation study of the water entry cavity of half hydrophobic-half hydrophilic sphere is performed. Particular attention is given to the simulation method based on solving the Navier-Stokes equations coupled with VOF model and CSF model. The numerical results are in agreement with the experimental results, thus validating the suitability of the numerical approach to simulate the water entry of sphere under different wetting conditions. Based on this method, the development of cavity created by the half hydrophilic-half hydrophobic sphere is investigated. Results show that the water entry of half hydrophobic-half hydrophilic sphere creates an asymmetric cavity and “cardioid” splash, which causes the sphere to travel laterally from the hydrophobic side to the hydrophilic side. Further investigations show that the fluid film presents during initial stage of impact, and on the half hydrophobic sphere, the fluid film detaches from the sphere to lead to cavity formation; on the half hydrophilic sphere, the fluid film moves up on the sphere surface and gathers at the vertex of the sphere, forming a wedge flow. The wedge flow moves and finally impacts on the opposite side of the cavity so as to cause “cardioid” splash. In addition, the total hydrodynamic force coefficient is investigated as a result of the forces acting on the sphere during water entry dictated by the cavity formation.

fluid mechanics; multiphase flow; half hydrophobic-half hydrophilic sphere; vertical water-entry; surface wettability; numerical simulation; cavity

2016-12-02

国家自然科学基金项目(11672094)； 哈尔滨市科技创新人才专项基金项目(2013RFLXJ007)

孙钊(1985—)， 男， 博士研究生。 E-mail: flame_1985@163.com

王聪(1966—)， 男， 教授， 博士生导师。 E-mail: alanwang@hit.edu.cn

TV131.2+2

A

1000-1093(2017)05-0968-10

10.3969/j.issn.1000-1093.2017.05.017