异结构不确定时变时滞复杂网络的外同步

王周洋顾佳佳 田静

（辽宁师范大学物理与电子技术学院，大连 116029）

异结构不确定时变时滞复杂网络的外同步

王周洋†顾佳佳 田静

（辽宁师范大学物理与电子技术学院，大连 116029）

本文研究了具有时间延迟的异结构不确定网络之间的外同步问题.基于Lyapunov稳定性理论，采用双向耦合自适应方法实现了两个结构互异的复杂网络之间的外同步.并且，网络的拓扑结构以及耦合强度也被同时确定.在数值模拟中，选取Van der Pol系统和Duffing系统作为网络节点进行仿真模拟，验证其理论结果的有效性.

异结构，双向耦合，外同步，参量识别，Lyapunov定理

引言

近年来，复杂网络同步以其在通信安全、物理学及自动控制等领域中的应用潜能，逐渐引起了学者们的研究兴趣［1-3］.许多文献已报道了有关网络中节点间的同步问题，即网络的内同步行为.然而，实际网络不仅存在内同步行为，也存在外同步行为.为此，Li等人首次提出将外同步作为一种新的同步方式，并说明了网络之间同步的可能性［4］.而后，许多学者在此基础上提出了多种实现网络外同步的方法［5-8］.另外，为更接近真实情况，研究的网络也逐渐涉及到不确定、时变、时滞等特性［9-11］.

值得注意的是，网络外同步的相关研究主要集中在驱动和响应网络是同结构的情况［12］.在现实世界中，还存在许多异结构网络间的同步现象.显然，研究具有时变时滞的异结构不确定网络之间的外同步对实际应用领域更具有借鉴性.目前，这类研究的相关报道还较少，同步的研究方法也相对单一，主要通过设计有效的控制器来实现异结构不确定网络的外同步.因此，在不加入控制器的情况下，如何通过网络之间的耦合作用实现网络的外同步是一项十分有意义的工作.

本文进行了具有时滞时变的两个异结构复杂网络之间的外同步研究.基于Lyapunov稳定性理论，运用双向耦合的自适应方法，不但实现了两个网络之间的外同步，而且网络的拓扑结构和网络节点之间的耦合强度也被同时确定.通过采用Van der Pol系统和Duffing系统分别作为两个网络的节点进行仿真模拟，发现网络之间的同步性能非常稳定.

1 网络与网络之间同步的机理分析

考虑由N个节点构成的复杂网络，由于耦合作用，网络具有下列形式

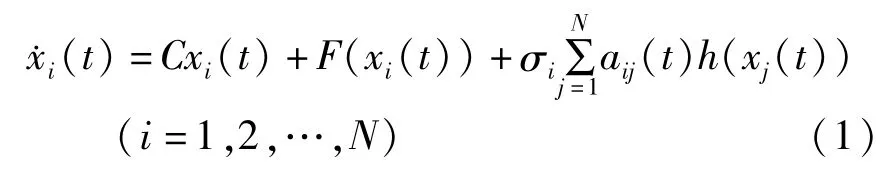
其中Cxi（t）是状态方程的线性部分，xi（t）∈Rn是网络第i个节点的状态变量，σi是网络内部节点之间的耦合强度，A＝（aij（t））N×N∈RN×N是表示网络拓扑结构的时变耦合矩阵.如果节点i和j之间存在连接，则aij（t）≠0，否则，aij（t）＝0.h（xj（t））是内部耦合方程.

现在，我们考虑下面两个具有双向耦合的时滞网络：这里＾σi是网络内部节点之间待定的耦合强度，τ是耦合延迟，ri和ki为耦合系数.

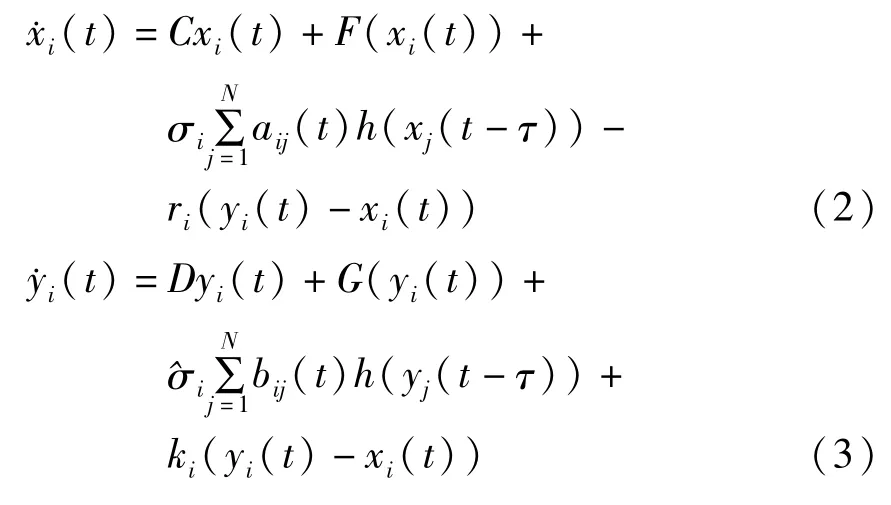
为了使两个网络之间达到同步，定义两个网络节点状态变量之间的误差为：

则误差随时间的演化关系为：

构造网络的Lyapunov函数：

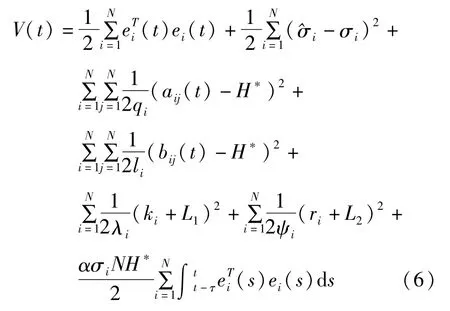
上式中qi、li、λi、ψi以及α是大于零的实数，H*是矩阵元aij（t）和bij（t）的配置参量.

则V的导数为：

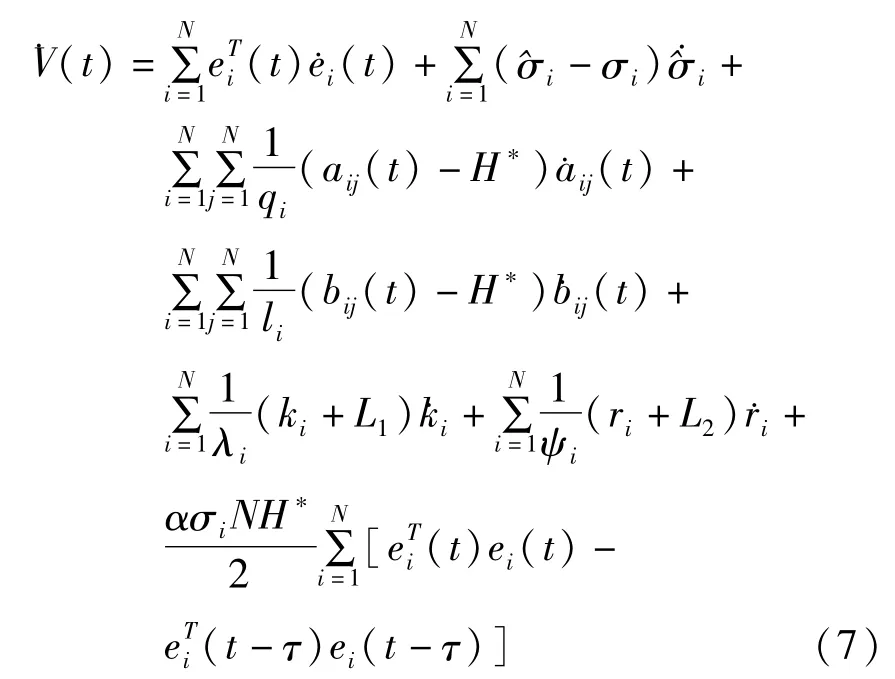
我们设计以下更新规则：

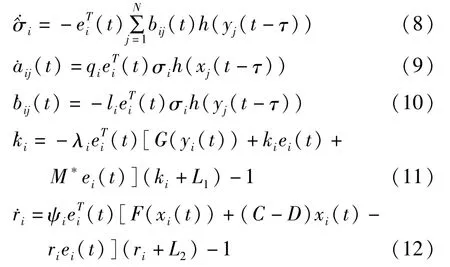
其中M*为配置参量.

将上述更新规则代入（7）式中，可以得到

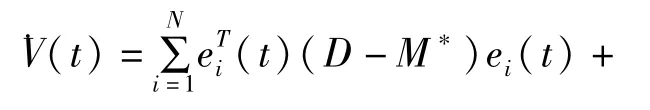
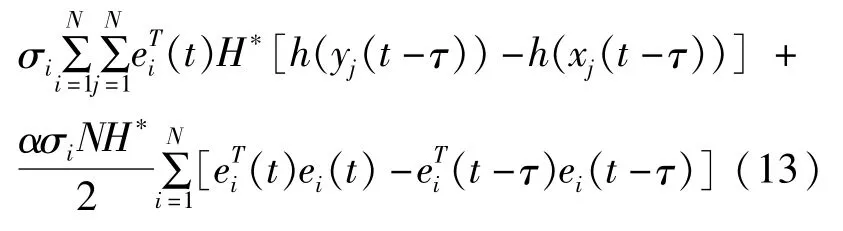
假设1：对于任意的x，y∈Rn，对于实数α＞0，下列关系成立：

引理1：对于任意向量x，y∈Rn，满足不等式：

将（16）式、（17）式代入（15）式中，可以得到：

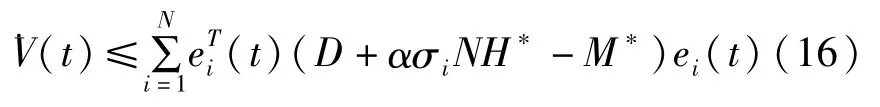
若配置参量M*满足M*≥D＋ασiNH*，则存在：

根据Lyapunov定理，两个不确定时变时滞网络的外同步得以实现.

2 仿真模拟

采用Van der Pol系统和Duffing系统分别作为两网络节点的状态方程进行仿真模拟，进而说明上述同步机理.

Van der Pol系统的状态方程具有下列形式：

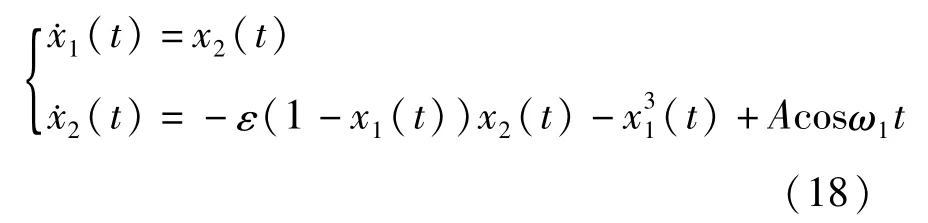
其中参量ε＝0.1，ω1＝1.

Duffing系统的动力学方程具有下列形式：

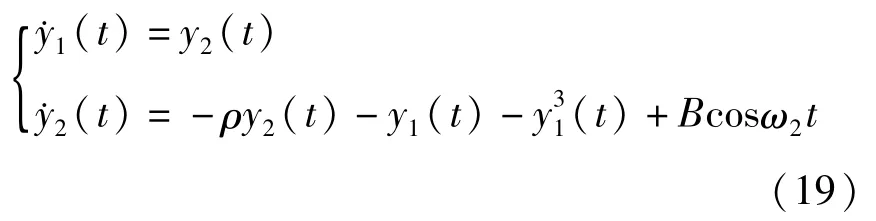
其中参量ρ＝0.18，ω2＝0.8.

仿真模拟时，选择网络节点数N＝5，为模拟方便，取耦合方程h（xi（t－τ））＝xj（t－τ），h（yi（tτ））＝yj（t－τ）.参量取值为qi＝15，li＝6，L1＝L2＝10，M*＝5，λi＝10，ψi＝15.同时，取耦合延迟τ＝0.1，耦合强度σi＝0.8，并假定第二个网络中的耦合强度是待定的.耦合矩阵元aij（t）和bij（t）的初值分别在（0，1）的区间内随机选取，其它各状态变量的初值均在（－1，1）的区间内随机选取.我们仿真模拟两个网络节点状态变量的误差ei（t）（i＝1，2，...5）随时间的演化规律如图1所示；运用更新规则（8）至（12），我们模拟出待定的耦合强度随时间的演化规律如图2所示；图3和4分别表示时变耦合矩阵元aij（t）、bij（t）随时间的演化图像.图5和6分别表示耦合系数ri、ki随时间的演化图像.

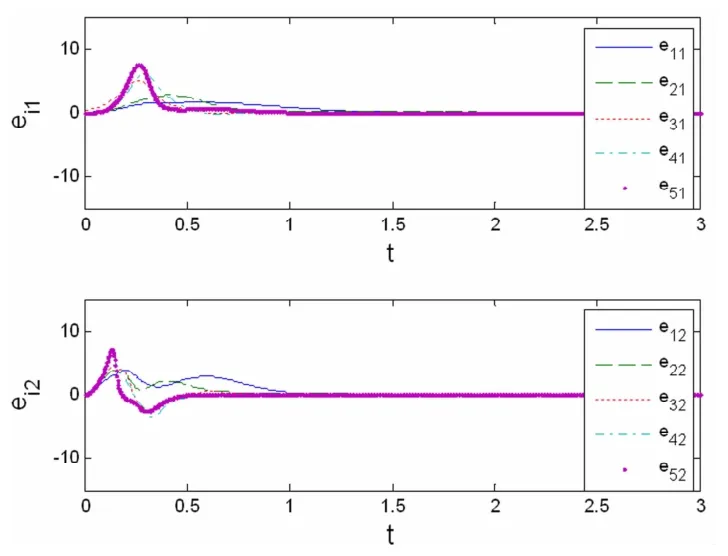
图1 误差ei（t）随时间演化图像Fig.1 Time history of the error ei（t）

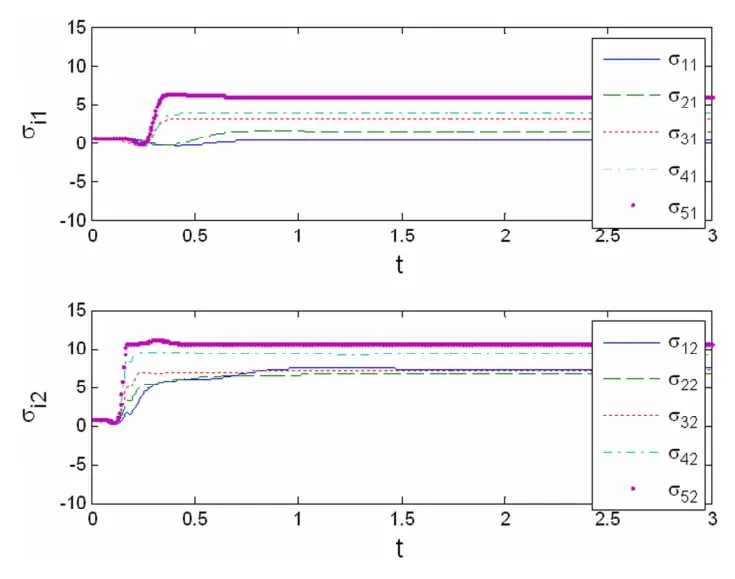
图2 耦合强度σi（t）随时间演化图像Fig.2 Time history of coupling strengthσi（t）

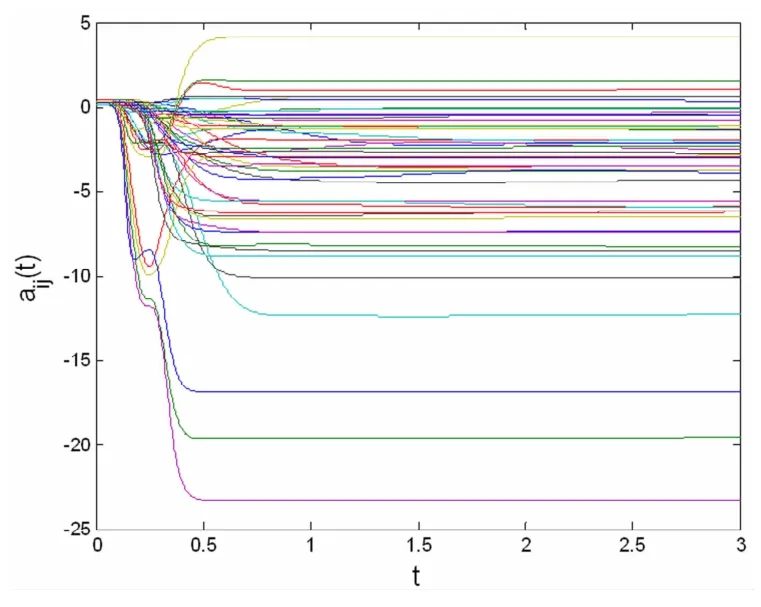
图3 耦合矩阵aij（t）随时间演化图像Fig.3 Time history of coupling matrix aij（t）

从图1可看出，网络在耦合连接初期，由于各节点状态变量所取初值不同，因此其误差ei＝（ei1，ei2）T（i＝1，2…，5）随时间演化的差异十分明显.但经过一个暂态过程后，两网络中对应的五个节点之间的误差变量随时间的演化均趋于零，意味着网络之间的外同步得以实现.另外，从图2至6中可看出，随着网络误差趋于零，网络耦合强度σi、耦合矩阵元aij（t）和bij（t）以及耦合系数ri和ki也趋于定值，即σi、aij（t）、bij（t）、ri、ki均被有效地识别.

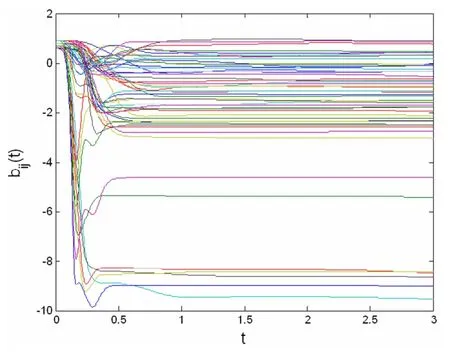
图4 耦合矩阵bij（t）随时间演化图像Fig.4 Time history of couplingmatrix bij（t）

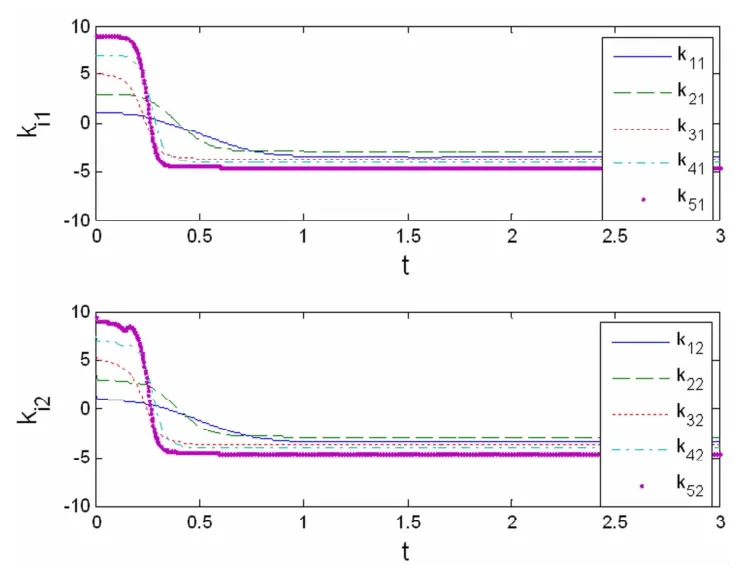
图5 耦合系数ri（t）随时间演化图像Fig.5 Time history of coupling parameter ri（t）

图6 耦合系数ki（t）随时间演化图像Fig.6 Time history of coupling parameter ki（t）

3 结论

仿真结果显示，对两个网络实施耦合后，经过一个短暂的过渡过程，两个网络节点之间达到了完全同步.同时，网络待定的耦合强度σi、时变耦合矩阵元aij（t）和bij（t）以及耦合系数ri和ki也被确定.

1 LüL，Li C R，Chen L S.Projective synchronization of the small-world delayed network with uncertainty.Nonlinear Dynamics，2014，76（2）：1633～1640

2 LiW L，Li C，Song H S.Synchronization between uncertain nonidentical networks with quantum chaotic behavior.Physica A Statistical Mechanics＆Its Applications，2016，461：270～277

3 Hindes J，Myers C R.Driven synchronization in random networks of oscillators.Chaos，2015，25（7）：73～119

4 Li C P，Sun W G，Kurths J.Synchronization between two coupled complex networks.Physical Review E，2007，76（6）：046204

5 Lu J，Ding C，Lou J，Cao J.Outer synchronization of partially coupled dynamical networks via pinning impulsive controllers.Journal of the Franklin Institute，2015，352（11）：5024～5041

6 Wu Z Y.Adaptive impulsive outer synchronization between drive-response dynamical networks.Communications in Theoretical Physics，2014，61（5）：590～594

7 Sun C X.Synchronization of chaotic neural networks with mixed time delays based on sliding mode control.Icic Express Letters，2015，9（1）：17～24

8 Xiang L Y，Zhu J JH.On pinning synchronization of general coupled networks.Nonlinear Dynamics，2011，64（4）：339～348

9 LüL，Chen L S，Bai SY，LiG.Synchronization between uncertain nonidentical networks with quantum chaotic behavior.Physica A Statistical Mechanics＆Its Applications，2016，460：314～325

10 Shi H，Sun Y，Miao L.Generation of lag outer synchronization of complex networks with noise coupling.Nonlinear Dynamics，2015，79（2）：1131～1140

11 Ma X H，Wang J A.Pinning outer synchronization between two delayed complex networks with nonlinear coupling via adaptive periodically intermittent control.Neurocomputing，2016，199（c）：197～203

12 Wu Y Q，Liu L.Exponential outer synchronization between two uncertain time-varying complex networks with nonlinear coupling.Entropy，2015，17（5）：3097～3109

Received 19 September 2016，revised 27 October 2016.

†Corresponding author E-mail：15242567959＠163.com

OUTER SYNCHRONIZATION BETWEEN TWO UNCERTAIN TIME-VARYING DELAYED COMPLEX NETWORKS WITH DIVERSE STRUCTURES

Wang Zhouyang†Gu Jiajia Tian Jing
（College of Physics and Electronic Technology，Liaoning Normal University，Dalian 116029，China）

Outer synchronization between two uncertain time-varying delayed networks with diverse structures is investigated in this paper.Based on Lyapunov stability theory，we achieve synchronization between two time-varying delayed networks with diverse structures by using bidirectional coupling adaptive method.The network topology and coupling strength are indentified simultaneously in the synchronization process.Finally，Van der Pol system and Duffing system are taken as nodes to constitute networks，and simulation is performed to verify the effectiveness of the method.

diverse structure，bidirectional coupling，outer synchronization，parameter identification，Lyapunov theorem

10.6052／1672-6553-2016-053

2016-09-19收到第1稿，2016-10-27收到修改稿.

†通讯作者E-mail：15242567959＠163.com