无信号控制人行横道的宽度设置方法研究

邹俊

（广州市市政工程设计研究总院，广东 广州 510060）

无信号控制人行横道的宽度设置方法研究

邹俊

（广州市市政工程设计研究总院，广东 广州 510060）

从行人过街的统计特征出发，通过实测采集无信号控制人行过街的相关数据，依据临界可插车间隙理论，对无信号人行过街的临界可插间隙进行了预测，并通过比较得出正态分布更优的结论，然后文章利用迭代计算的方法对无信号人行横道宽度进行求解，并针对广州某具体交叉口进行了案例分析。研究成果可为城市无信号控制人行横道的设置提供参考。

无信号人行道；临界可插间隙；人行横道宽度

0 引言

步行交通具有占用道路资源少、绿色环保、可达性高等诸多优势，是符合“以人为本”、“绿色交通”等交通发展理念的重要出行方式之一。但由于其在速度、反应时间等方面的劣势，又往往在各类交通方式中处于“弱势地位”。尤其是在无信号控制的路段或交叉口人行横道处，车辆通行的速度通常较高，行人需根据车辆到达间隙择机通过，若人行横道设计不合理，则很容易诱发人车相撞的事故。

在进行无信号人行横道设计时，人行横道宽度是一个十分关键的设计参数，需要依据车流量大小、行人过街需求、道路几何设计等因素综合确定。过宽的人行横道不仅占用道路资源，同时会导致行人过街的离散性增大，不利于机动车驾驶员决策；而过窄的人行横道则会导致行人间相互干扰增加，同样不利于交通安全和效率。因此关于无信号人行横道宽度的研究，对保障交通安全，促进步行出行具有重要意义。

研究人行横道宽度问题，首先离不开对于行人过街规律的研究。该问题的研究要点是在一定的车流量输入下，研究行人如何利用车辆间隔完成过街行为的问题，即研究行人临界可插车间隙的问题，常用到的研究手段是统计回归分析。国内外 已 有 较 多 此 方 面 的 研 究 成 果 ， 如 Raff 法 、Ashworth 法、Lag 法、Logit 模 型 、极大 似 然估 计 法等。而接下来的重要工作则是研究如何利用所掌握的行人过街规律来和里的设计人行横道宽度。目前关于这方面的研究较少，《城市道路交叉口设计规程 CJJ 152-2010》 也仅是根据不同道路等级给出推荐的阀值，无法根据不同的车流及人流大小进行精细的分析与设计[1-5]。

本文采用极大似然估计的方法研究行人临界可插车间隙问题，并利用迭代计算的方法求解无信号人行横道的宽度问题，以期为人行横道设计提供依据和参考。

1 行人临界可插车间隙特性研究

1.1 模型的提出

本文采用极大似然估计确定行人临界可插车间隙。该方法认为临界可插车间隙服从概率分布，而非某固定值，较符合实际规律；同时该方法可充分利用最大拒绝间隙及接受间隙数据，并以个体为单位进行分析，结果更具说服力。

首先应确定临界可插间隙的分布形式。一般对过街行人而言，其临界可插间隙是一个适中的值，选择较小或较大间隙的行人较少。因此，tc的概率分布应是一条中间高，两侧低的曲线，那么我们不妨分别假设 tc服从正态分布和对数正态分布两种常见的分布形式，进行参数求解并评价拟合效果。

对于驾驶者 i而言，临界间隙出现在 ri与 ai之间的概率是 Fc（ai）-Fc（ri）。考虑所有驾驶者，则其似然函数为式中：ai、ri，若服从正态分布，则分别为接受间隙和最大拒绝间隙；若为对数正态分布，则取其对数。

该似然函数的对数为：

为 L 使取得最大值，则 μ 与 σ2应满足：

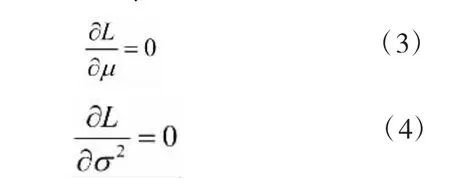
为满足式（3）及式（4），则可利用下述方法迭代求解：

假设已知 σ2的值，则可利用方程

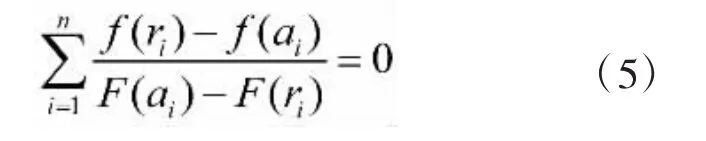
估计 μ 值。本文 σ2初始值取值为 2.5。当利用式（5）得到了一个较好的 μ 值后，则可利用式（6）算得一个较好的 σ2值。式中 μ 即为式（5）估计得到的值。

根据式（5）、式（6）所述方法进行反复迭代运算，则可得到符合精度要求的 μ 值及 σ2值。

1.2 函数拟合

本文选取图1所示的广州市建设横马路与建设六马路 T 型交叉口开展调查，共采集 130 位行人的过街信息。

图1 行人过街行为采集点

采集数据主要存在如下问题：

（1）某些行人会在遇到的第一个车头时距选择穿越，对于此类行人，无法采集拒绝的车头时距；

（2） 某些行人拒绝的最大车头时距不足 1 s，这并不表示行人的过街行为激进，而是由于车辆到达较密，行人未获得更大的拒绝间隙；

（3）某些行人接受的车头时距过长，在 20 s 以上。这并不表示行人过街行为保守，而是此类行人恰巧碰到了较大的插车间隙。

基于上述分析，为尽量保证统计结果准确，则规定如下：

当行人无最大拒绝间隙或最大拒绝间隙小于2 s 时，令其最大拒绝间隙为 2 s；

当行人接受的车头时距在 15 s 以上时，令其接受的最大车头时距为 15 s。

接下来，可利用式（5）式及式（6）进行迭代求解，当其结果均为 0 时迭代终止。但实际上，这样的条件是难以达到的。不妨令式（5）式左侧绝对值为 Δ1，式（6）等式左侧绝对值为 Δ2。则迭代得到相关参数，见表1。

表1 正态分布与对数正态分布相关求解参数

通过比较，正态分布拟合的 Δ1、Δ2值更接近0，且极大似然值更大，说明拟合效果更优，因此选取正态分布作为本文的拟合函数。利用结果可绘制 接 受 概 率 分 布 Fa（t），拒 绝 分 布 Fr（t）及 临 界 可 插间隙分布 Fc（t）的关系见图2。

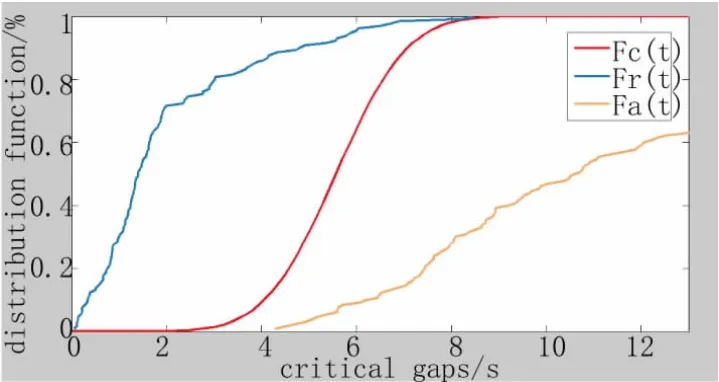
图2 Fa（t）、Fr（t）、Fc（t）关系图

2 求解方法

设人行横道宽度 Wc，行人横向间距 W，则人行横道每一行所能容纳的最大行人数为 N=[Wc/w]+1人。在分析人行横道通行能力 C时，只需研究人行横道每一纵列通行能力 c，则总通行能力 C=N·c。设计人行横道宽度时，须保证通行能力大于行人需求，以确保安全和效率。

由于车辆到达和行人临界插车间隙的双重随机性，直接利用概率学知识推导人行横道通行能力较为困难，因此本文采用迭代计算的方法对问题进行求解。

3 实例分析

本文选取位于广州市河滨北路与河滨南路的两处人行横道开展实例分析。

河滨北路人行横道位于从化博物馆门前,其东侧布设有公交车站和滨江公园,而河滨南路人行横道位于大型住宅小区与滨江绿道之间，因此该两处人行横道过街的过街需求较大，且由于是无信号控制形式，河滨路的车流对人行过街造成一定影响。以此为背景，本文对该两处人行横道展开研究分析。

调查点位见图3，相关交通调查结果见表2。

图3 实例分析调查点位

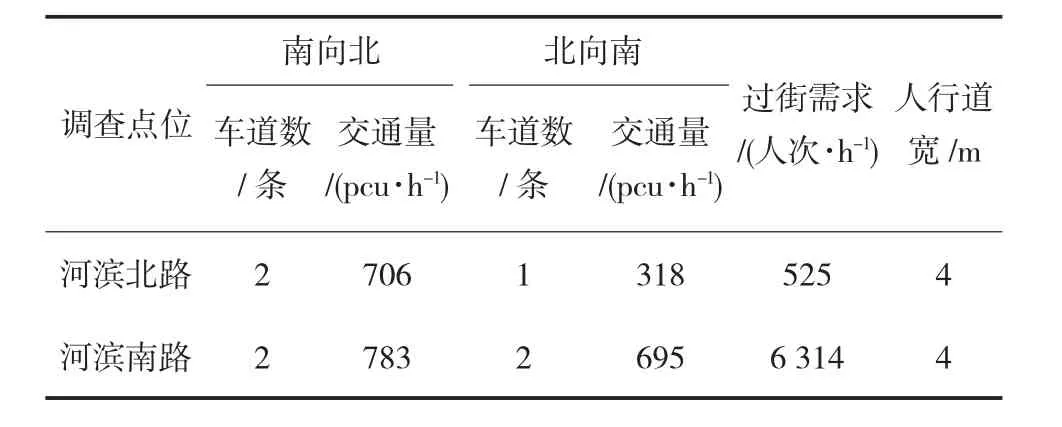
表2 实例路段及路口交通参数

根据此前对行人过街行为的调查结果，设定行人过街的临界可插车间隙服从均值 μ=5.57，方差 σ2=1.39 的正态分布，前后行人跟驰时距 tf=3 s,行人穿越车流时间 tp=4 s，行人间的横向间距为 1 m。为了综合权衡行人过街的安全和效率，人行横道的饱和度不宜过高或过低，本例选取饱和度为0.7。利用本文提出的模型计算法，计算得到两个点位应设置的人行道宽度及饱和度见表3。

表3 实例分析计算结果

比较表2及表3数据可以发现，目前两点位的人行横道设置较为合理，其中河滨北路的人行横道宽度略高于推荐值，因此可根据实际情况进行优化调整。

4 结语

本文综合运用交通工程、交通流、统计学等方面知识，探讨了无信号人行横道通的临界可插间隙特征和人行横道宽度设计问题，在如今市政建设追求以人为本理念和精细化设计的背景下,本文的研究成果有一定实际应用价值。

[1] 邓雪, 赖旭. 成都市无信号交叉口行人过街临界间隙分布研究[J].交通运输工程与信息学报 2014(12）:109-114.

[2] 美国交通研究委员会.道路通行能力手册[M].北京:人民交通出版社,2008.

[3] 王殿海,严宝杰.交通流理论[M].北京:人民交通出版社,2002.

[4] 赵伟涛,钱大琳,杨彦青.行人穿越人行横道临界间隙研究[J].武汉理工大学学报（交通科学与工程版）,2012,36(4）:808-811.

[5] 金光浩,荣建,边扬.路段无信号控制人行横道行人过街服务水平研究[J].武汉理工大学学报,2012,34(7）:61-66.

U412.37+8

:B

:1009-7716（2017）05-0252-03

10.16799/j.cnki.csdqyfh.2017.05.071

2017-03-06

邹俊（1971-），男，广东河源人，高级工程师，从事市政道路、交通路网规划设计工作。