基于workbench的蜗杆有限元模态分析

高启林

摘要： 本文主要对蜗杆的模态进行了相关分析，使用Pro-e绘图软件建立不同参数下的蜗杆模型，通过workbench有限元软件对其模态进行了相关分析，得到了相关参数的变化对蜗杆各阶固有频率的影响，具有一定的工程价值。

Abstract： This paper is about the Modal Analysis of Worm. The model of the Worm is built by Pro-e software. The Anslysis of the Modal is using the the finite element software Workbench. And we obtaine the related parameters of change on the influence of the natural frequencies and worm， which has a certain engineering value.

关键词： 蜗杆；模态分析；有限元；固有频率

Key words： Worm；Modal Analysis；finite element；natural frequency

中图分类号：TH132.44 文献标识码：A 文章编号：1006-4311（2017）16-0204-03

0 引言

蜗杆传动是一种重要的传动方式，具备传动比大，承载能力高，传动平稳，且易于自锁的特点，在国防、冶金、建筑 、化工等行业得到广泛的运用。蜗杆作为一种机械传动构件，传动过程中产生振动会对蜗杆的工作造成一定的影响。模态分析作为其它动力学分析的起点，如瞬态动力学分析，使用模态分析来确定蜗杆的振动特性，分析参数变化对蜗杆振动性能的影响，在工程实践中具有重要的作用。本文通过有限元软件workbench对蜗杆模态进行了分析，考虑不同参数下的蜗杆的固有频率，寻找参数改变对蜗杆固有频率的影响，对蜗杆的工程运用具有一定的帮助。

1 有限元模型建立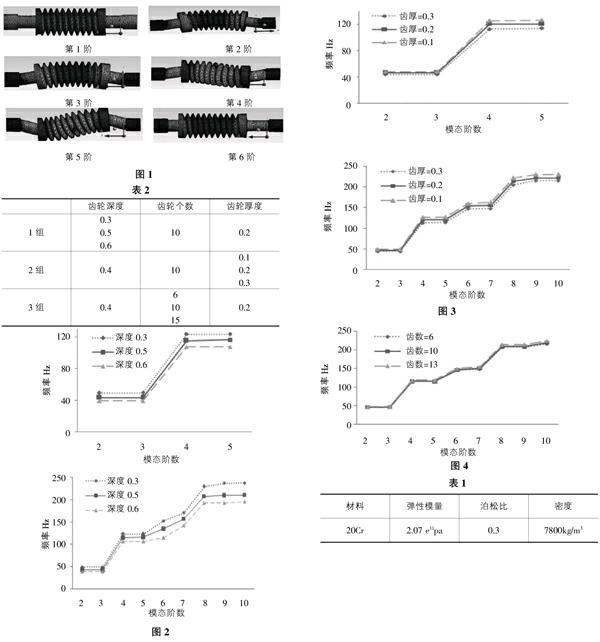

由于workbench有限元软件在建立复杂模型方面存在了一定技术难度，本文采用绘图软件Pro-e通过参数控制建立蜗杆三维实体模型。有限元法是将无限多个自由度的物体化为有限多个自由度的物体，通过相关函数进行差值，得到一组多未知量的多元线性代数方程组，最后通过边界条件求解问题。通过Pro-e建立三维模型，workbench中支持多种模型格式的导入，通过比较，Pro-e中SAT格式可较好的导入workbench中。

2 workbench有限元分析

2.1 前处理

2.1.1 单元类型

有限元分析中单元类型对分析结果有很大的影响，通过查寻得使用的单元类型为高阶3维10节点固体结构单元SOLD187单元，该单元通过10个节点来定义，每个节点有3个沿着X，Y，Z方向的平移自由度，具有很好的二阶位移模式可以很好地模拟不规则图形，满足需求。

2.1.2 定义材料相关参数与网格的划分

本文蜗杆采用的材料为20Cr，相关参数如表1。使用workbench对模型进行自由划分网格。

2.1.3 约束

模态分析中，唯一有效的载荷是零唯一约束，其他类型的载荷，如力、压力、温度等，可以在模态分析中制定，但是在模态提取时将被忽略。在模态分析中约束条件十分重要，它可以影响到零件振型和固有频率，在分析中需要仔细考虑模型是受到什么样的约束。蜗杆运动模式是绕定轴旋转，且在两侧的阶梯轴端面安装滚动轴承支撑。因此我们需要约束其X，Y，Z轴方向的位移，及沿X，Y轴方向的绕轴转动，通过Workbench中Remote Displacement，约束其相应的位移及转动。

2.2 模态分析及结果

2.2.1 相关理论

2.2.2 workbench分析结果

①本次对蜗杆参数的分析属于定性分析，模型的建立并不是按实物尺寸建立，为了保证我们建立模型分析的可靠性，求得前6阶振型图如图1所示。

第1阶振型图蜗杆自身刚体运动；第2阶及3阶振型图蜗杆中心处分别沿着轴，Y轴产生微小的位移；第4阶及5阶振型为图蜗杆中心分别沿Y轴，X轴方向产生微小转动位移，第6阶振型图蜗杆产生轴向拉压变形，通过文献中的类似蜗杆的振型图比较，确定我们所建立的模型建立的可靠性。

②我们对蜗杆的分析主要研究蜗杆齿轮厚度，齿轮的深度，及齿轮的个数改变对模态的影响，具体如表2所列。

第一组蜗杆：

研究在蜗杆其它条件不变的情况下，齿轮深度分别为：0.3，0.5，0.6时的蜗杆固有频率，提取前10阶频率结果如图2所示。

由于前几阶固有频率变化值较所取单位值过小，因此分别提取了2～5及2～10阶频率作图，由图知，随着齿轮深度的增加，蜗杆的固有频率在逐渐降低。并且随着阶数的升高降低的幅度也在增加。

第2组蜗杆：

研究蜗杆在其它条件不变情况下，齿轮厚度分别为：0.1，0.2，0.3时的蜗杆固有频率，提取前10阶频率结果如图3所示。

同上，我们分别提取2～5阶及2～10阶频率，通过图形可知，随着齿轮厚的的增加，其固有频率在逐渐降低，但是就影响而言，齿轮厚度对其固有频率变化影响没有深度变化那么明显。

第3组蜗杆：

研究在其它条件不变的情况下，齿数为6，10，15时候的蜗杆模态，提取前10阶固有频率，如图4所示。

从图中可以看出，在蜗杆其它条件不变的情况下，齿数为6， 10， 13的蜗杆其前8阶固有频率曲线几乎重合，只有在8阶过后，我们看到稍微的分界线，因此可以得出，在其它条件均不变的情况下，蜗杆的齿数的增减对其前几阶固有频率的影响非常微小。

3 结论

通过三维绘图软件Pro-e及有限元软件workbench对蜗杆进行了模态有限元分析，通过分析，我们得到了蜗杆模态的前6阶振型图。通过蜗杆参数的控制，设计不同的蜗杆进行了分析，分别得到了蜗杆不同参数下的模态，通过比较分析，我们发现，在蜗杆的模数及尺寸等其他条件不变的情况，改变蜗杆的齿数对其前几阶固有频率影响非常微小，而改变蜗杆齿轮的深度则对其固有频率有较大的影响。

参考文献：

[1]濮良贵.机械设计[M].北京：高等教育出版社，1996：235-238.

[2]张洪才.ANSYS14.0理论解析与工程应用实例[M].北京：机械工业出版社，2013（08）：327-328.

[3]劉北辰.工程计算力学理论与运用[M].北京：机械工业出版社，1994（06）：164-166.

[4]唐熊武，袁建畅，沈丹峰.基于 ANSYS 的阿基米德蜗杆模态分析[J].机械传动，2010（10）：62-65.

[5]凌桂龙.ANSYS Workbench 15.0从入门到精通[M].北京：清华大学出版社，2014：134-153.

[6]刘广禄，郭嘉.基于 ABAQUS 的圆弧圆柱蜗杆模态分析[J]. 机械研究与运用，2016（03）：1-6.