中国财政政策、货币政策的就业效应

牟俊霖+闫里鹏

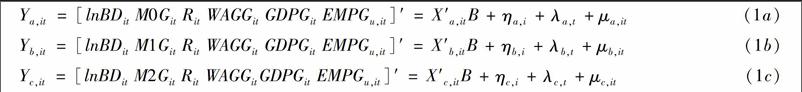
摘要：以中国省级面板数据为基础，采用面板向量自回归模型估计了财政政策、货币政策对中国就业与经济增长的影响，结果发现：第一，扩张性财政政策对城镇就业和经济增长都有很强的促进作用；第二，增加货币供给的扩张性货币政策对城镇就业的促进作用有限，然而对经济增长有很强的促进作用；第三，降低利率的货币政策对城镇就业和经济增长的促进作用有限，并且要滞后两年才能显现出来。因此，为了促进就业增长，应当以扩张性的财政政策为主，同时辅之以增加货币供给的扩张性货币政策，以发挥其促进经济增长的作用，从而夯实就业增长的基础。鉴于利率对就业和经济增长的影响具有滞后性，应当保持利率政策的稳定性。

关键词：财政政策；货币政策；就业；面板向量自回归模型

一、引言

近年来，中国经济增长率持续下降，从2011的9.2%下降到2015年的6.9%，与此同时中国的就业形势保持相对稳定，2011-2015年期间年均新增就业岗位1286万个，城镇登记失业率维持在4.1%左右。在未来的一段时期内，中国经济仍将面临增速调整和结构调整的问题，而经济增速的调整将不利于总就业的增长，经济结构的调整有可能产生大量的结构性失业，因此经济增速和结构的调整不可避免地会对中国的就业产生负面的冲击。为此，中国政府应当采取恰当的财政政策和货币政策稳定就业形势，为中国经济增长的转型升级赢得更多的时间。但是，财政政策和货币政策对中国的就业到底有多大的促进作用呢？现有的研究并没有给出明确的结论。

有大量的文献研究了财政政策、货币政策对中国就业的影响，其中卢亮、刘新和刘星、董万好和刘兰娟、张宏亮等研究了财政政策对中国就业的影响；许先普、李伊涵和陈利锋、易定红和白九梅研究了货币政策对就业的影响，然而尚未有文献在同一个理论框架和计量模型中研究财政政策和貨币政策对就业的影响。不仅如此，现有研究的结论存在显著的差异，甚至存在较多矛盾之处：第一，关于财政政策对中国就业的影响，卢亮、董万好和刘兰娟发现财政政策对中国就业有积极的促进作用，然而刘新、刘星发现财政政策对中国就业没有显著的促进作用；第二，关于货币政策对中国就业的影响，李伊涵和陈利锋、易定红和白九梅发现货币政策对中国就业有显著的促进作用，然而许先普发现货币政策对中国就业有不利的影响。

综上所述，已有的研究割裂了财政政策和货币政策的相互影响关系，没有在财政政策和货币政策可以相互作用的理论框架下来估计财政政策、货币政策对就业的影响。不仅如此，现有研究并没有对财政政策、货币政策的就业效应达成一致的认识。因此，我们尚不清楚财政政策、货币政策对中国就业贡献的大小，我们也不能根据现有研究的结论提出具有针对性的政策建议。为此，我们需要采用新的数据和新的研究方法评估中国财政政策和货币政策的就业效应，以便提出更具有针对性的政策建议。

在这样的背景下，本文根据1991-2014年的省级面板数据，采用面板向量自回归模型估计财政政策和货币政策对中国就业的影响。本文的创新主要有三点：第一，采用新的方法——面板向量自回归模型——估计了财政政策和货币政策的就业效应，这是一种积极的尝试；第二，本文采用财政赤字作为度量扩张性财政政策的变量，从而更好地解决了财政政策的识别问题；第三，本文在同一个模型中估计了财政政策和货币政策对就业的影响，从而能够比较财政政策和货币政策的就业效应的大小，进而能够提出更加具有针对性的政策建议。

二、文献综述与方法选择

关于财政政策、货币政策对中国就业的影响，现有研究采用的研究方法各不相同，因而得出了不同的研究结论。总体而言，现有研究主要采用了如下五种研究方法：第一，卢亮以凯恩斯的宏观乘数理论为基础，测算了政府支出乘数、税收乘数和转移支付乘数，进而测算出财政支出对新增就业的贡献大约为4%；第二，董万好、刘兰娟建立了一个分析财政科教支出对就业及产业结构调整影响的可计算的一般均衡模型（CGE），发现财政科教支出对就业有积极的促进作用，特别是对于住宿和餐饮等劳动密集型产业的就业有较强的促进作用；第三，刘新、刘星估计了财政社会保障支出与就业之间的面板协整模型，发现财政社会保障支出对就业有一定的促进作用，张宏亮估计了财政支出与就业之间的协整模型，发现20世纪90年代以后财政支出对就业的促进作用大幅度下降，而曾学文分别估计了财政支出、国债发行、货币供给与就业之间的协整模型，发现财政政策、货币政策的就业促进作用不理想；第四，易定红、白九梅通过时间序列模型估计了利率波动性对失业影响，发现利率波动与失业率之间存在负相关的关系；第五，李伊涵、陈利锋采用了向量自回归模型研究了流通中现金量和社会信贷余额与就业之间的关系，发现社会信贷余额的就业效应大于流通中现金量的就业效应。

综上所述，已有的研究采用的研究方法主要有宏观乘数法、可计算的一般均衡模型、协整模型、多元时间序列的回归模型、向量自回归模型等五种方法，但是在这些方法中哪种方法更加适合于研究财政政策、货币政策对中国就业的影响呢？现有研究并没有对这个问题进行深入地讨论。事实上，财政政策和货币政策对就业的影响主要具有如下三个特征：第一，财政政策、货币政策对就业的影响具有动态特征，也就是说财政政策、货币政策对就业的影响在政策实施之后的几个时期内都是存在的；第二，财政政策、货币政策对就业的影响具有时效性，我们主要关心的是经济衰退时期扩张性的财政政策、货币政策对就业的影响，因此我们主要研究财政政策、货币政策对就业的短期影响关系，而不是研究二者对就业的长期影响关系；第三，财政政策、货币政策外生冲击的识别问题，这是因为财政政策、货币政策是通过政府的外生干预而实施的，但是政府的干预过程是不可测量，从而成为遗漏变量进入了误差项，导致了内生性问题，应当采取恰当的方法识别财政政策、货币政策的外生冲击。根据上述三个特点，我们认为宏观乘数法、可计算的一般均衡模型、多元时间序列的回归模型、协整模型都不是研究财政政策、货币政策就业效应的最佳方法，因为前三者不能考查财政政策、货币政策对就业的动态影响关系，而后者不能集中考查财政政策、货币政策对就业的短期影响关系。因此，我们应当采用向量自回归模型研究财政政策、货币政策对就业的影响。但通常来说，采用向量自回归模型必须要解决外生政策冲击的识别问题以及样本量较少带来的估计结果不稳健的问题，因为这些问题直接影响了向量自回归模型估计结果的准确性。

关于外生政策冲击的识别问题，目前主要有如下三种解决方法：第一，西姆斯（Sims）提出的短期零限制条件识别方法，这种方法也称为递归识别法，该方法假定政策变量在当期对其他经济变量不产生影响，那么结构型向量自回归模型A中矩阵A为下三角矩阵，矩阵B为对角矩阵，从而可以采用乔里斯基（Choleski）分解的方法确定矩阵A和B，但是伯南克（Bernanke）和布林德（Blinder）指出变量排列顺序对这种识别方法的分解结果有重要的影响，因此建议把政策变量排在所有变量的第一位；第二，布兰查德（Blanckard）和柯（Quah）以及布兰查德和佩罗蒂（Perotti）提出的长期零限制条件识别方法，该方法的思路是，把结构型的向量自回归模型转化为u_t=A^-1Bu_t=Cu_t的形式，然后根据残差u_t与结构型冲击u_t的长期关系确定矩阵C中部分元素的具体值，从而识别出政策的外生冲击，但是这种识别方法面临的最大问题是，需要预先通过经济理论和相关数据对模型中的关键参数进行估计，如果我们选取的理论和数据出现偏误，则采用该识别方法估计出来的结果将是不准确的；第三，尤里格（Uhlig）提出的符号限制的识别方法，这种方法通过设定一定时期内一组变量之间的相关关系来识别政策的外生冲击，比如帕帕（Pappa）通过假定财政支出与总产出和财政赤字正相关的方法识别了财政政策的外生冲击，卡诺瓦（Canova）和帕帕通过假定财政收入与总产出和财政赤字负相关的方法识别了财政政策的外生冲击，博蒙特（Berument）等则通过假定利率与货币供给和通货膨胀负相关的方法识别了货币政策的外生冲击。

关于向量自回归模型样本量较少、回归结果不稳健的问题，已有研究致力于把向量自回归模型扩展为面板向量自回归模型，从而充分利用面板数据样本量大、估计结果稳健的优点。但是，估计面板向量自回归模型面临如下两个重要的问题：第一，由于模型引入了因变量的滞后项而产生了内生性问题；第二，面板数据模型固有的不可观察的个体效应。霍尔茨一埃金（Hohz-Eakin）等最早把向量自回归模型扩展为面板向量自回归模型，并且提出了采用内生变量和外生变量的滞后项作为内生变量的工具变量的方法，估计了面板向量自回归模型。阿雷拉诺（Arellano）和邦德（Bond）首先通过一阶差分的方法去除了横截面的个体效应，然后采用变量的水平值的滞后项作为差分变量的工具变量，最后通过广义矩估计的方法估计了动态面板模型，这种方法称为一阶差分广义矩估计。由于一阶差分会损失很多的信息，阿雷拉诺和邦德以及布伦德尔（Blundell）和邦德提出了采用前向均值差分的方法去除个体效应，然后采用水平变量的滞后项作为差分变量的工具变量，采用差分变量的滞后项作为水平变量的工具变量，最后采用广义矩估计的方法同时估计了水平方程和差分方程，这种方法称为系统广义矩估计。以系统广义矩估计为基础，洛夫（Love）和泰克尼诺（Zicchino）采用前向均值差分的方法去除个体效应，然后采用广义矩的估计方法估计了面板向量自回归模型，这是最早采用广义矩方法估计面板向量自回归模型的文献，其后有大量的文献采用该方法估计了面板向量自回归模型。如果面板数据具有较强的异质性，那么就应当采用如下的两种估计方法去除面板数据的异质性：第一，佩斯卡拉（Pesaran）等提出的混合组均值估计方法，该方法首先对每个横截面分别进行估计，然后对各个横截面的回归系数进行加总和统计推断；第二，斯瓦米（Swamy）提出的面板随机系数模型，即假定自变量的各个横截面的系数与其均值的差服从均值为0、标准差为Ω的正态分布，多恩等（Doan）进一步假定标准差Ω服从明尼苏达先验分布，从而可以采用贝叶斯估计方法估计面板随机系数模型，卡诺瓦和奇卡雷利（Ciccarelli）以及卡诺瓦等随后对该方法进行了发展和完善。

综上所述，我们应当采用向量自回归模型研究财政政策、货币政策的就业效应，并且向量自回归模型的最新发展方向是外生政策冲击的识别以及面板向量自回归的估计。在本文中，我们采用省级面板數据研究财政政策、货币政策对中国就业的影响，为了识别财政政策和货币政策的外生冲击，我们采用短期零限制条件识别方法和符号限制的识别方法，为了匹配省级面板数据同质性较强的特征，我们采用广义矩估计方法估计面板向量自回归模型。

三、计量模型、估计方法与数据

1.政策冲击的识别

为了得到稳健的估计结果，本文采用了两种识别政策冲击的方法：第一，借鉴短期零限制条件识别方法，我们把外生性最强的财政政策、货币政策变量放在面板向量自回归模型中各变量的最前面，把内生性较强的变量——国内生产总值、工资、就业——放在财政政策、货币政策变量之后；第二，根据符号限制的识别方法，财政赤字比财政收入、财政支出更适合于测量财政政策，因此本文不再使用财政收入或者财政支出作为测量财政政策的变量，而是采用财政赤字作为测量财政政策的变量。不仅如此，我们还引入了财政支出的相对增长率，即财政支出与收入的增长率之差来识别财政政策冲击，这是因为财政支出的增长率高于财政收入的增长率，财政支出的相对增长率提高，就意味着政府采取了扩张性的财政政策，反之亦然。值得注意的是，由于货币政策涉及货币供给和利率两个方面的变量，而且我们不能对这两方面的变量进行简单的整合，因此本文未能参考符号限制的识别方法识别货币政策冲击，而是把货币供给变量和利率变量共同带入面板向量自回归模型中，以研究货币供给和利率对就业的影响。

2.变量选择与描述性统计

假定y_t是企业t期的总产出，λ是企业t期的生产技术，K_t是企业t期使用的资本，E_t是企业t期的就业量，P_t是t期的除利率之外的其他政策变量，根据巴罗（Barro）对生产函数的设定方式，把除利率之外的其他政策变量P_t引入柯布一道格拉斯生产函数中，得到生产函数y_t假定w_t是t期劳动者的工资r_t是t期的利率，根据利润最大化条件得到就业函数E_t=根据就业函数，影响就业的主要变量有总产出、工资、利率以及除利率之外的其他政策变量。

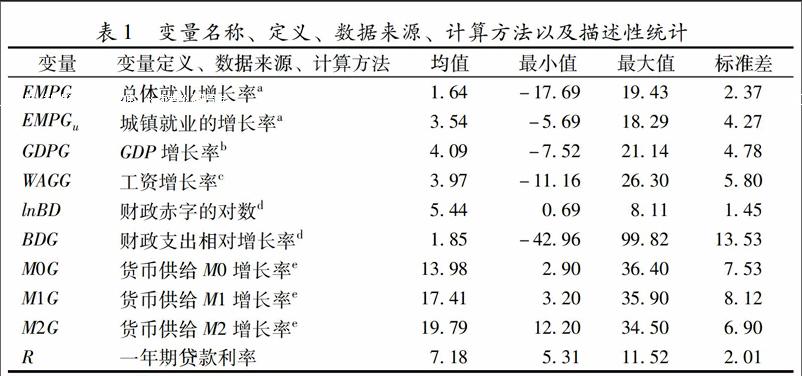
在本文中，测量总产出的变量是国内生产总值GDP，测量就业的变量是总体就业EMP和城镇就业EMP_u，测量工资的变量是城镇单位从业人员平均工资WAG，测量利率的变量是一年期贷款利率尺，测量财政政策的变量是财政赤字BD和财政支出的相对增长率BDG（财政支出与财政收入的增长率之差），测量货币政策的变量是货币供给MO、M1、M2以及一年期贷款利率R。对于上述各变量还有如下四点说明：第一，总体就业EMP和城镇就业EMP的数据来源于各省市历年的统计年鉴，其他数据来自《新中国六十年统计资料汇编》以及《中国统计年鉴》（2009-2015），同时由于《中国统计年鉴》只提供了1991年以后的货币供给M0、M1、M2的可比价格增长率的数据，因此本文中各变量的样本区间为1991-2014年；第二，根据林（Im）等提出的面板单位根检验，我们发现变量EMP、EMP、GDP、WAG、MO、M1、M2以及这些变量的对数均存在单位根，因此本文采用这些变量的增长率EMPG、EMPG、GDPG、WAGG、MOG、M1G、M2G，而财政赤字BD不存在单位根，因此本文采用财政赤字的对数lnBD；第三，货币供给增长率MOG、M1G、M2G、一年期贷款利率R是全国年度时间序列数据，样本期间为1991-2014年，样本量为24个，而其他变量是1991-2014年期间的省级面板数据，样本量为31x24=744个；第四，城镇就业增长率EMPG_u的最大值为44.74，最小值为-21.84，因此该变量存在不合理的异常值，我们对EMPG进行了2%的缩尾处理。本文采用的各变量的名称、定义、数据来源、计算方法、描述性统计，参见表1。

3.模型的设定与估计方法

从理论上讲，我们应当把测量货币政策的四个变量MOG、M1G、M2G、R带入同一个面板向量自回归模型中，但是变量MOG、M1G、M2G、R是全国时间序列数据，并且变量MOG、M1G、M2G之间存在较强的相关性，如果把这四个变量带人同一个面板向量自回归模型中，则该模型不能被估计出来。因此，我们把变量MOG、M1G、M2G分别带人下面的三个面板向量自回归模型中：

因为省级面板数据具有较强的同质性，所以本文采用阿雷拉诺和邦德以及布伦德尔和邦德提出的系统广义矩估计方法估计向量自回归模型，估计程序来自洛夫和泰克尼诺提供的Stata命令。

四、面板向量自回归模型的估计结果

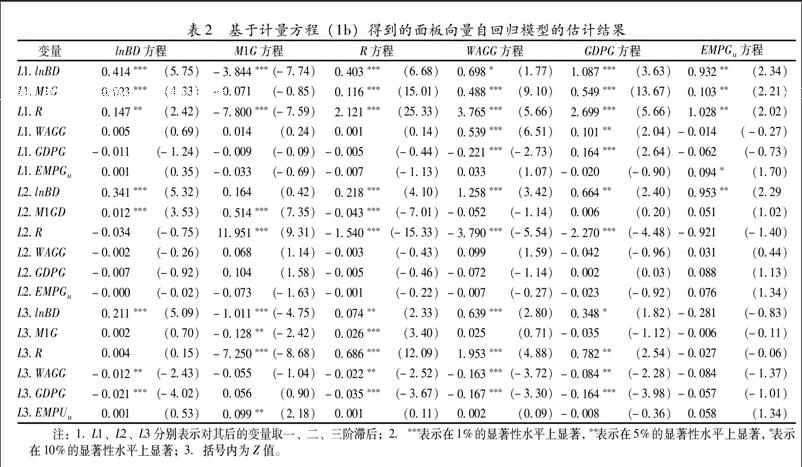
在估计面板向量自回归模型之前，我们需要进行以下三个方面的检验①：第一，根据林（Im）等提出的面板单位根检验，我们发现，变量EMPG、EMPG、WAGG、GDPG、lnBD、BDG、MOG、M1G、M2G、R都是平稳的变量，故而适合采用面板向量自回归模型进行估计；第二，根据BIC、AIC、HQIC三个信息准则，我们发现，面板向量自回归模型（1a）、（1b）、（1c）的最优滞后阶数为五阶，但是采用五阶滞后得到的估计结果和脉冲反应图效果不理想，所以我们把最优的滞后阶数调整为三阶，把各内生变量的工具变量的滞后阶数调整为四阶；第三，根据稳定性检验，我们发现，九個面板向量自回归模型都是不稳定的，其原因是模型中加入了MOG、M1G、M2G、R四个时间序列变量，如果要得到稳定的面板向量自回归模型，就必须去除这四个变量，然而这将导致我们不能考察货币政策对就业的影响，不能比较财政政策、货币政策对就业影响的大小关系，为了避免这两方面的不利影响，我们在面板向量自回归模型中保留了MOG、M1G、M2G、R四个变量，同时采用bootstrap的方法对估计结果进行1000次的蒙特卡洛模拟，以尽可能地消除模型的不稳定对估计结果的影响。面板向量自回归模型的研究重点是，根据估计方程得到残差的方差协方差矩阵，然后再对方差协方差矩阵进行分解，进而得到相应的脉冲反应图，限于篇幅的限制，我们没有给出所有面板向量自回归模型的估计结果，仅给出了基于计量模型（1b）的回归结果，参见表2。如表2所示，模型中有较多变量在10%的显著性水平上显著，因此可以对估计方程的方差协方差矩阵进行分解，并得到相应的脉冲反应图。

1.财政赤字、货币供给增长率、利率对就业的影响分析

根据面板向量自回归模型（1a），我们可以得到总体就业增长率EMPG、城镇就业增长率EMPG_u，对财政赤字对数lnBD、货币供给MO的增长率MOG、利率R的脉冲反应图形，参见图1。

如图1所示，总体就业增长率EMPG对财政赤字的对数lnBD、货币供给MO的增长率MOG、利率尺的脉冲反应图分布在[-0.4，0.4]的区间之内，而城镇就业增长率EMPG_u对财政赤字的对数lnBD、货币供给MO的增长率MOG、利率R的脉冲反应图分布在[-0.5，1.5]的区间之内。这表明，财政政策、货币政策对总体就业的影响较小，而对城镇就业的影响较大。这是因为，总体就业包含了农业从业人员，而农业从业人员具有稳定、不受经济周期波动影响的特征，故而财政政策、货币政策对总体就业的影响较小，而城镇就业容易受到经济周期波动的影响，故而财政政策、货币政策对城镇就业的影响更大。鉴于财政政策、货币政策对总体就业的影响较小，本文不再研究财政政策、货币政策对总体就业的影响，而是集中研究财政政策、货币政策对城镇就业的影响。

图1下方的三幅子图显示了财政政策、货币政策对城镇就业增长率EMPG.的影响：第一，在四年以内，财政赤字的对数lnBD对城镇就业增长率EMPG.有显著的正向影响，这表明，增加财政赤字能够有效地促进城镇就业的增长；第二，货币供给MO的增长率MOG对城镇就业增长率EMPG.的影响在零水平线上下波动，且在较多情况下为负数，这表明，提高货币供给增长率MOG对城镇就业没有显著的促进作用；第三，提高利率R，在两年以内对城镇就业增长率有正向影响，在两年以后对城镇就业增长率EMPQ有负向影响，这意味着，降低利率R在两年以内对城镇就业增长率有负向影响，在两年以后对城镇就业增长率EMPG_u有正向影响。上述结论表明，在经济衰退时期，采取降低利率的政策在短期对城镇就业有不利的影响，这是因为降低利率就降低了企业使用资金的成本，这将促使企业采用相对更加便宜的资本来替换劳动，从而降低了城镇就业，而降低利率的政策从长期来看对城镇就业有积极的促进作用，这是因为长期的低利率政策可以刺激消费和投资，提高企业的利润空间，促使企业扩大生产规模，进而促进城镇就业增长。

总体而言，扩张性的财政政策能够在短期内对城镇就业产生很强的促进作用，而增加货币供给MO的扩张性的货币政策对城镇就业没有显著的促进作用，降低利率的扩张性货币政策在短期内对城镇就业有负向影响，因此扩张性财政政策对城镇就业的促进作用大于扩张性货币政策对城镇就业的促进作用，这一研究结论与曾学文的研究结论相似。

为了观察和比较货币供给增长率MOG、M1G、M2G对城镇就业的影响，我们估计了面板向量自回归模型（1a）、（1b）、（1c），并得到城镇就业增长率EMPG_u对财政赤字的对数lnBD、货币供给增长率M0G、M1G、M2G、利率尺的脉冲反应图形，参见图2。

第一，如图2第一列所示，在财政赤字的对数lnBD分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，财政赤字的对数lnBD对城镇就业增长率EMPG.的影响分布在[-0.5，2]的区间，而且在四年内均有显著的正向影响，这表明扩张性财政政策对城镇就业有显著的促进作用；第二，如图2第二列所示，货币供给增长率M0G、M1G、M2G对城镇就业增长率EMPG_u的影响分布在[-0.5，0.5]的区间之内，且围绕零水平线上下波动，这表明增加货币供给M0、M1、M2的扩张性货币政策对城镇就业没有显著的促进作用；第三，如图2第三列所示，在降低利率尺的货币政策分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，利率对城镇就业增长率EMPG的影响分布在[-0.5，0.5]的区间之内，且在两年以内基本为负数，在两年以后为绝对值较小的正数，这表明降低利率的货币政策对城镇就业的促进作用有限，且具有滞后性。

综上所述，当扩张性财政政策分别与增加货币供给M0、M1、M2的扩张性货币政策搭配使用的时候，扩张性财政政策对城镇就业有及时、强健的促进作用，增加货币供给M0、M1、M2的扩张性货币政策对城镇就业没有显著的促进作用，降低利率尺的扩张性货币政策只有在两年以后才会对城镇就业产生一定的促进作用，我们的研究结论与卢亮、董万好、刘兰娟、曾学文的研究结论相似，与许先普的研究结论相反。

2.财政支出相对增长率、货币供给增长率、利率对就业的影响分析

为了检验上述研究结论是否稳健，我们采用财政支出相对增长率BDG作为测量财政政策的变量，根据面板向量自回归模型（2a）、（2b）、（2c），得到城镇就业增长率EMPG对财政赤字相对增长率BDG、货币供给增长率MOG、M1G、M2G以及利率尺的脉冲反应图形，参见图3。

如图3第一列所示，在财政赤字相对增长率BDG分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，财政赤字相对增长率BDG对城镇就业增长率的不同影响分布在[-0.5，1.0]的区间之内，且在三年以内为绝对值较大的正数，在三年以后为绝对值较小的负数，这表明，不论与何种增加货币供给的扩張性货币政策搭配使用，扩张性财政政策对城镇就业均有显著的、较强的促进作用。

如图3第二列所示，货币供给增长率MOG、M1G、M2G对城镇就业增长率的不同影响分布在[-0.5，0.5]的区间之内，且围绕零水平线上下波动，这表明，增加货币供给M0、M1、M2的扩张性货币政策对城镇就业没有显著的促进作用。

如图3第三列所示，在降低利率尺的货币政策分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，利率对城镇就业增长率的影响分布在[-0.5，0.5]的区间之内，因而对城镇就业的促进作用有限。具体而言，降低利率的货币政策在两年以内对城镇就业有显著的抑制作用，在两年以后对城镇就业有一定的促进作用，在四年以内对城镇就业的累计净促进作用趋近于零。

总而言之，当采用财政支出相对增长率作为测量财政政策的变量的时候，我们依然可以得到如下基本结论：扩张性财政政策在短期内对城镇就业有很强的促进作用，增加货币供给M0、M1、M2的扩张性货币政策对城镇就业没有显著的促进作用，降低利率的扩张性货币政策至少在两年以后才会对城镇就业产生一定的促进作用。

3.财政赤字、货币供给增长率、利率对经济增长的影响分析

经济增长和就业稳定是宏观经济调控的两个重要目标，如果财政政策、货币政策对就业与经济增长的影响存在差异，那么宏观调控政策就应当在促进就业和保持经济增长两个政策目标中有所取舍。因此，研究财政政策、货币政策对经济增长的影响，有助于我们提出更加具有针对性的政策建议。根据面板向量自回归模型（1a）、（1b）、（1c），我们得到经济增长率GDPG对财政赤字对数lnBD、货币供给增长率MOG、M1G、M2G、利率尺的脉冲反应图形，参见图4。

如图4第一列所示，在财政赤字对数lnBD分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，财政赤字对数lnBD对经济增长率GDPG的影响均呈现出逐渐下降的趋势，且三年内为绝对值较大的正数，三年后为绝对值较小的负数，说明扩张性财政政策对经济增长有较强的促进作用。

如图4第二列所示，货币供给增长率MOG、M1G、M2G对经济增长率GDPG的影响呈现出“几”字型的变化趋势，而且在三年以内为绝对值较大的正数，在三年以后为绝对值很小的负数，这说明增加货币供给的扩张性货币政策对经济增长也有很强的促进作用。

如图4第三列所示，当降低利率R的货币政策分别与货币供给增长率MOG、M1G、M2G搭配使用的情况下，降低利率R在两年以内对经济增长率GDPG有较强的负面影响，在两年以后对经济增长率GDPG有一定的促进作用。这说明，降低利率的货币政策对经济增长的促进作用较小，而且需要滞后两年的时间才能凸显出来。这是因为，在经济萧条时期，企业和消费者对经济前景的预期趋于悲观，降低利率不会迅速地刺激消费和投资的增长，反而促使企业采用资本替换劳动，因而在短期内对就业和经济增长产生了不利的影响，如果在较长的时期实行低利率的货币政策，则可能提高企业的利润空间，促使企业扩大生产规模，从而促进了经济增长和就业。

综上所述，增加财政赤字的扩张性财政政策以及增加货币供给的扩张性货币政策对中国经济增长均有较强的促进作用，但是降低利率的扩张性货币政策对中国经济增长的促进作用有限，而且需要滞后两年的时间才会凸显出来。

4.面板向量自回归模型估计结果的稳健性分析

在面板向量自回归模型中，更换变量的排列顺序对模型的分解结果有一定的影响。为了检验变量的排列顺序对本文研究结论的影响，我们重新估计了更换变量排列顺序的面板向量自回归模型（3a）、（3b）、（3c），并得到相应的脉冲反应图①。我们发现，财政赤字的对数lnBD对城镇就业增长率EMPG的促进作用依然是最强的，货币供给增长率MOG、M1G、M2G对城镇就业增长率EMPG有一定的促进作用，但是远小于财政赤字的对数lnBD对城镇就业增长率EMPGa的促进作用，降低利率R只有在两年以后才会对城镇就业增长率EMPQ有一定的促进作用。因此，在更换变量的排列顺序之后，本文的研究结论依然成立，本文的研究结论具有较强的稳健性。

五、研究结论与政策建议

本文以中国省级面板数据为基础，采用面板向量自回归模型估计了财政政策、货币政策对中国就业以及经济增长的影响，我们主要发现如下四点结论。

第一，由于农业从业人员对经济周期和宏观调控政策不敏感，扩张性财政政策和扩张性货币政策对中国总体就业的影响很小，但是扩张性财政政策和扩张性货币政策对中国城镇就业的影响较大，因而扩张性财政政策和扩张性货币政策应当着力于促进中国城镇就业的增长。

第二，扩张性财政政策对中国城镇就业有及时的、强健的促进作用，不仅如此，扩张性财政政策对中国经济增长也有很强的促进作用，因此扩张性财政政策能够在短期内稳定就业形势并恢复就业增长，是经济衰退时期保就业、稳增长的最重要的宏观调控政策。

第三，增加货币供给的扩张性货币政策对中国城镇就业的促进作用非常有限，然而增加货币供给的扩张性货币政策对中国经济增长有很强的促进作用，因此在经济衰退时期可以采用增加货币供给的扩张性货币政策刺激经济增长，但不宜采用增加货币供给的扩张性货币政策促进就业。

第四，降低利率的货币政策对中国城镇就业和经济增长的促进作用有限，并且需要滞后两年的时间才能显现出来，因此降低利率的货币政策也不能成为经济衰退时期稳定就业形势、恢复就业增长的主要宏观调控政策。

综上所述，扩张性的财政政策对中国城镇就业和经济增长均有很强的促进作用，而增加货币供给的扩张性货币政策对城镇就业的促进作用有限，但是对经济增长有很强的促进作用，降低利率的货币政策对城镇就业和经济增长的促进作用有限且需要较长的时间才能凸显出来。因此，我们建议，为了稳定就業形势并促进就业增长，应当以扩张性财政政策为主，这要求政府在就业形势恶化的时候，适时地推出财政刺激政策防止失业加剧和就业形势的进一步恶化。与此同时，还应当辅之以增加货币供给的扩张性货币政策，以发挥其对经济增长的促进作用，尽快恢复经济增长，通过经济增长助推就业增长，为就业增长提供经济增长的支撑。鉴于利率对就业和经济增长的影响具有一定的滞后性，因此利率的调整应当慎重，应当根据就业和经济形势坚持把利率长期维持在一个适当的水平。