大偏离度非球面检测畸变校正方法

高松涛，武东城，苗二龙

(中国科学院 长春光学精密机械与物理研究所应用光学国家重点实验室 超精密光学工程研究中心，吉林 长春 130033)

大偏离度非球面检测畸变校正方法

高松涛*，武东城，苗二龙

(中国科学院 长春光学精密机械与物理研究所应用光学国家重点实验室 超精密光学工程研究中心，吉林 长春 130033)

在高数值孔径(NA)投影光刻物镜中，随着数值孔径的增加，非球面的偏离度越来越大。对这种大偏离度非球面进行亚纳米量级的检测，一直是光学检测的一大难题。本文首先对一偏离度超过500 μm的偶次高次非球面进行了计算全息图(Computer-Generated Hologram,CGH)设计，设计出了满足高精度面形检测和刻蚀加工要求的CGH。然后，针对此设计方案，定量分析了CGH的成像畸变及畸变对像差分析的影响。分析结果表明，不同径向位置的成像倍率偏差(畸变)最大达到了2.7∶1，并且由于畸变的存在，低阶像差衍生出了明显的高阶像差。最后，针对用CGH检测大偏离度非球面时出现的成像畸变，提出了采用光线追迹与最小二乘法相结合的成像畸变的校正方法，并通过实验验证了此方法的准确性。实验结果表明，畸变校正之后相对剩余残差小于0.2%，可以满足高精度非球面检测加工的要求。

计算全息图；CGH；畸变；非球面检测

1 引 言

随通常情况下，光学系统的数值孔径越大，光线的入射角就越大，系统的像差就越难校正。此时如果采用非球面元件，则可以大大增加光学设计优化的自由度，从而在降低光学系统复杂度的同时，提升光学系统的成像质量。正是由于非球面存在诸多优点，在高NA投影光刻物镜中，都普遍采用非球面元件来提升像质[1-2]。对于投影光刻物镜而言，随着NA的增加，不仅非球面的数量在增加，非球面的偏离度及梯度也在逐步增加[3-4]。对于这种大偏离度的非球面进行亚纳米量级的检测，一直是光学检测领域的一大难题。

目前，要实现对非球面的高精度检测，一般都采用零位补偿法，即利用补偿镜[5-7]或者CGH[5,8-9]，将干涉仪发出的球面波转化为与非球面匹配的非球面波，从而实现零位检测。当非球面的偏离度梯度过大时，补偿镜的设计往往较为困难，并且由于其含透镜数量过多(可达4～6片)，补偿镜的绝对精度很难保证。CGH作为二元衍射元件，其相位可以直接根据非球面方程及光路配置获得，只要CGH的刻线不过于密集，并且多余的衍射级次不造成鬼像，从原理上来看，CGH可以实现对大偏离度非球面的高精度检测。

在实际应用中，用CGH检测大偏离度非球面时，往往会出现很大的成像畸变。系统的成像畸变主要来源于两个方面，一方面是干涉仪，另一方向是CGH。当前商用干涉仪的成像畸变一般较小，往往可以忽略。CGH在将干涉仪发出的球面波转换为非球面波的同时，往往会引入成像畸变；并且非球面偏离度(或偏离度梯度)越大，成像畸变越大。成像畸变破坏了CCD像素坐标到实际镜面坐标的线性映射关系，一方面使测量数据与镜面实际位置发生错位，若用检测的数据指导光学加工(特别是离子束面形精修，IBF)，会影响光学加工的收敛性，另一方也会影响像差的分析精度。如果采用有效的畸变校正方法，可以实现高精度校正成像畸变，从而消除上述两方面的影响。

当前，众多论文在对成像畸变进行校正时，一般都采用“标记点”法[10-14]，即在被测面的特定位置上做标记点，进行面形检测之后，提取出标记点在CCD坐标的位置，根据标记点在镜面坐标和CCD坐标的对应关系，利用特定的算法校正畸变。由于提取大量的标记点坐标比较费时费力，并且坐标提取往往存在误差，所以“标记点”法一般适合于畸变相对较小、对畸变校正精度要求不高的系统。如果成像畸变较大，并且对畸变校正精度要求苛刻，则需要考虑采用新的畸变校正方法。为了解决这一问题，论文针对一偏离度达到575 μm的高次非球面，首先设计出了满足高精度面形检测和刻蚀加工要求的CGH，然后定量分析了CGH所引入的畸变大小及畸变对像差分析的影响，最后采用光线追迹与最小二乘法相结合的方法，实现了对畸变的精确校正，并在实验上对校正精度进行了验证。

2 非球面检测方案

2.1 非球面方程

对于偶次高次非球面，其方程可以表示为[15]：

(1)

图1 非球面的偏离度和非球面梯度 Fig.1 Departure and slope of the asphere

式中，z为非球面矢高，R为顶点曲率半径，κ为二次曲面常数，An为高阶项系数，M为高阶项阶数，ρ为非球面的径向坐标。非球面的具体参数如表1所示，非球面偏离度及非球面梯度如图1所示。从图1可以看出，此非球面的偏离度达到了575 μm，最大梯度为48 μm/mm。

2.2 CGH的设计

CGH作为一种常用的检测非球面的方法，其工作原理及设计方法已经非常成熟，众多文献[16-19]给出了CGH相位和空间频率的计算方法，论文此处不再赘述。但需要注意的是，CGH到非球面的距离、CGH到干涉仪焦点的距离需要恰当选择，从而使得CGH的刻线不过于密集，同时又可以避免多余衍射级次的鬼像。对于凹面非球面，在设计时一般选择将CGH置于干涉仪焦点外侧[16-17,19-21]；但对于表1中所示的非球面，由于其非球面偏离度过大，如果选择此种方案，为了实现对衍射级次的分离，需要增大CGH到干涉仪焦点的距离，最终使得干涉仪腔长达到2 m。为了尽量减小干涉腔长，提高测量精度，考虑将CGH置于干涉仪焦点内侧，最终选择了类似凸面的检测方案，如图2(a)所示；该方案采用15.24 cm F/7.3 TS(Transmission Sphere)，CGH前表面距离干涉仪焦点位置为-1 000 mm，CGH距离非球面距离为190 mm。CGH刻线的空间频率如图2(b)所示，最大的空间频率为269 mm-1，对应的刻线最小周期为3.72 μm，满足加工要求。

表1 非球面参数

图2 用CGH检测非球面的光路图和CGH刻线的空间频率 Fig.2 Light path of testing asphere with CGH and spatial frequency of CGH

3 CGH的成像畸变及其对像差的影响

3.1 CGH的成像畸变

根据图2(a)所示的检测光路图，在Zemax软件中，为了查看CGH的畸变，将非球面设为光阑，将Aperture Type设置为“Float By Stop Size”，并开启“Ray Aiming”功能，非球面与参考面上的Footprint分别如图3(a)与图3(b)所示。由于非球面为光阑，因此光线在非球面上实现了等间隔采样；在参考面上，均匀的网格变的“扭曲”，此即为CGH引入的畸变。

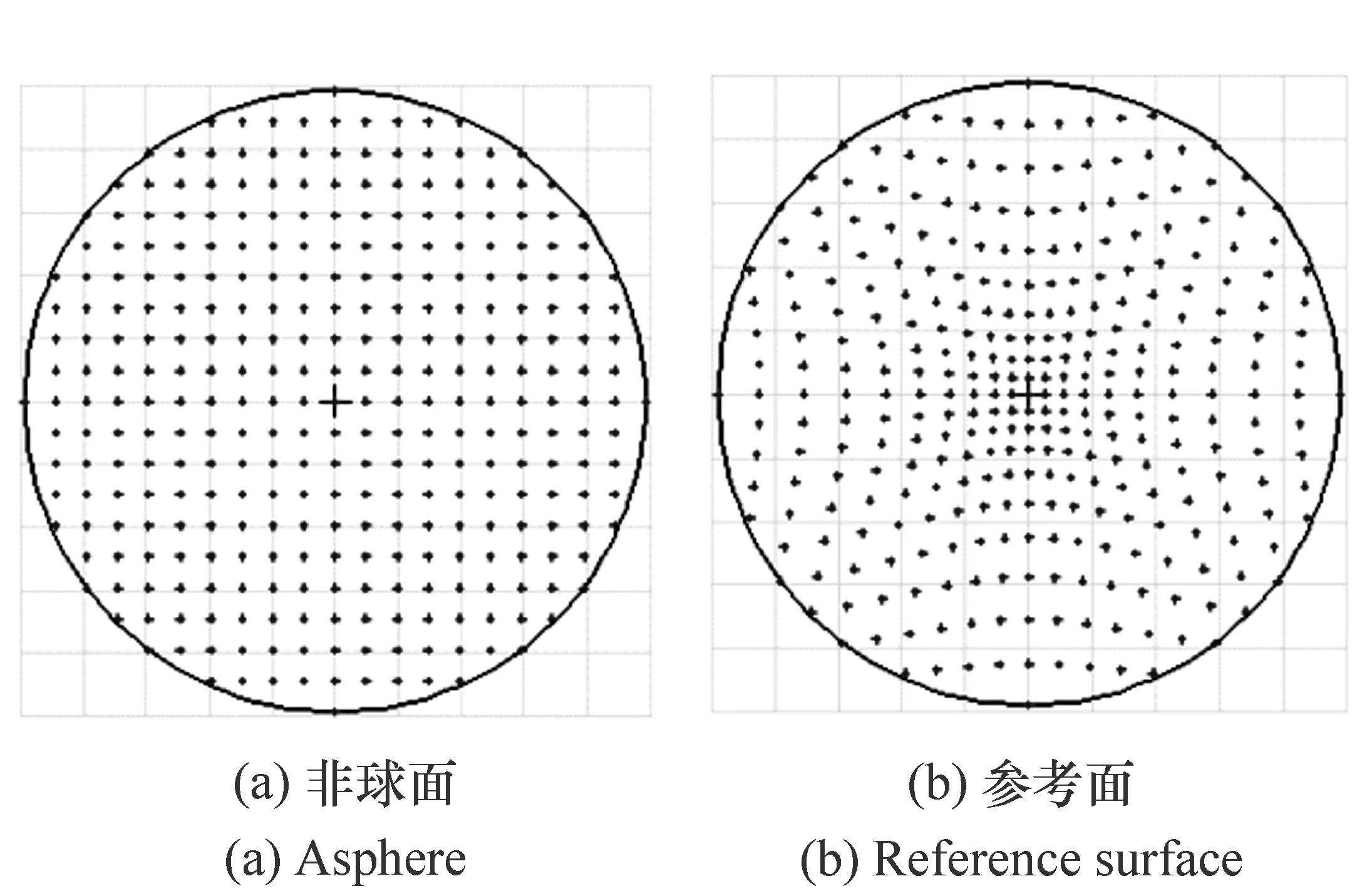
图3 非球面与参考面上的Footprint Fig.3 Footprint of asphere and reference surface

图4 非球面不同的径向位置在CCD上的分辨率 Fig.4 CCD resolution for the different radial positions of asphere

假设CCD有效像素数为Zygo干涉仪CCD像素数，非球面在CCD上所占的径向尺寸比例为60%，忽略干涉仪自身的畸变，通过光线追迹可以获得非球面不同的径向位置在CCD上的分辨率，如图4所示；从图4中可以看出，不同的径向位置分辨率差别极大，最大值与最小值分别为0.46 mm/pixel和0.17 mm/pixel。

3.2 成像畸变对像差分析的影响

对图2(a)所示的光路进行波像差分析，或者对非球面的测量结果进行分析时，一般都会用到Zernike多项式。通过将波面误差用Zernike进行拟合，从而获得各种像差的成分，即

(2)

式中，W(ρ,θ)为波面误差，Zn(ρ,θ)为条纹Zernike的第n项，cn为第n项Zernike系数。

考虑到整个光学系统旋转对称，非对称畸变(如偏心畸变)非常小，往往可以忽略。对于径向畸变，存在如下关系[14]:

(3)

式中，k3、k5和k7等是畸变系数。

以条纹Zernike的第三项(y方向倾斜)为例来分析畸变对像差的影响，若不存在畸变，则:

(4)

若存在畸变，将式(3)带入式(4)，则有:

(5)

从式(5)可以看出，如果存在畸变，倾斜(Z3)会衍生出彗差(Z8)和高阶彗差(Z15、Z24等)；与倾斜类似，离焦(Z4)会衍生出球差(Z9)和高阶球差(Z16、Z25等)。实际上，只要存在畸变，低阶像差都会衍生出更高阶的像差。

为了更直观的观察畸变对像差分析的影响，可以在Zemax软件中进行仿真分析。对于图2(a)所示的检测光路，若非球面倾斜0.001°，分别以非球面和参考面为光阑，对应的干涉图及波面的Zernike系数如图5所示。以非球面为光阑时，实现了在非球面上均匀采样，非球面倾斜引入的主要像差为倾斜(彗差及高阶彗差非常小)；以参考面为光阑时，光线在参考面上均匀采样，但由于CGH存在较大的成像畸变，分析结果将受到畸变的影响，所以像差除了倾斜外，还包含彗差与高阶彗差，与式(5)的分析结果相符。所以，在用图2(a)所示的检测光路进行分析时，需要将非球面设置为光阑，从而避免CGH的成像畸变对像差分析造成影响。

图5 非球面倾斜0.001度时，分别以非球面和参考面为光阑，仿真获得的干涉图与Zernike系数；(a)以非球面为光阑时的干涉图；(b)以参考面为光阑时的干涉图；(c)以非球面为光阑时的Zernike系数；(d) 以参考面为光阑时的Zernike系数 Fig.5 Interferograms and Zernike coefficients generated by simulation when the asphere and reference surface are set as stop respectively, and the tilt of asphere is set 0.001 degree; (a)Interferogram when the asphere is set as stop. (b)Interferogram when the reference surface is set as stop. (c)Zernike coefficients when the asphere is set as stop. (d)Zernike coefficients when the reference surface is set as stop

4 畸变校正与实验验证

4.1 畸变校正

设非球面上的径向坐标为ρAsp，与之对应的参考面和CCD的坐标分别为ρRef和ρCCD，考虑到CGH的成像畸变，则有:

(6)

式中，k1表示放大倍率系数，k2n-1(n≥2)表示畸变系数，N表示总项数。

若干涉仪的畸变可以忽略，则:

(7)

式中，t为放大倍率系数。

设非球面的通光口径半径为RAsp，与之对应的参考面和CCD坐标分别为RRef和RCCD，将式(7)带入式(6)，并将坐标进行归一化，则:

(8)

利用图2(a)所示的光路图，采用光线追迹法，可以获得rAsp和rRef；而后利用式(8)，选定多项式项数，采用最小二乘法，可以获得拟合出系数{s2n-1}；最后利用获得的拟合系数和式(8)，通过插值法即可完成对干涉图(相位图)的畸变校正。当采用不同的畸变阶数进行拟合时，拟合残差如图6所示；从图6中可以看出，由于畸变较大(特别是高阶畸变较大)，只有采用较高的拟合阶数，才能达到较高的拟合精度(残差最大偏差小于0.1像素)。对于这种高次多项式的拟合，为了达到较高的精度，往往需要很多的采样点，如果采用传统的“标记点”法，往往非常费时费力，并且标记点的提取精度也会影响最终的校正精度；但如果采用光线追迹法，则会更加方便高效。

图6 采用不同的拟合阶数进行拟合时的剩余残差 Fig.6 Fitting residuals when using different fitting orders

需要注意的是，上述分析过程，忽略了干涉仪本身畸变的影响。实际上，如果可以获得干涉仪内部的光学参数，干涉仪自身的成像畸变也可以通过光线追迹获得。但对于普通商用的干涉仪，干涉仪内部光学参数往往是不公开的，因此不能采用光线追迹法获得干涉仪的畸变。不过当前商用干涉仪的畸变往往都很小，如果可以忽略，则可以方便的利用上述方法来实现对畸变的精确校正。

4.2 干涉仪成像畸变

为了明确干涉仪自身畸变的大小，采用“标记点”法对畸变进行测量。首先，在镜面上用激光打标机做“+”形标记；然后用影像仪测量标记点真实的坐标位置；最后，在干涉图中提取标记点在CCD坐标下的位置，如图7所示。通过对比标记点的真实坐标位置与CCD坐标位置，从而可以获得干涉仪的畸变。计算结果表明，干涉仪的成像畸变约为0.08%，干涉仪成像畸变可以忽略不计。

图7 (a)带有标记点的干涉图；(b)在干涉图中提取标记点坐标 Fig.7 (a)Interferogram with fiducials; (b)Extracting the coordinates of fiducials on the interferogram

图8 CGH的实物图 Fig.8 Image of CGH

4.3 实验验证

图9 (a)畸变校正之前的干涉图；(b)畸变校正之后的干涉图 Fig.9 (a)Interferogram before correcting distortion; (b)Interferogram after correcting distortion

针对图2(a)所示的CGH设计方案，加工制作了CGH，如图8所示，并用此CGH完成了对非球面的检测。为了从实验上验证4.1中所论述的畸变校正方法，用数控机床在非球面上做了均匀网格标记点，畸变校正前后的干涉图如图9所示。从图9(a)上可以看出，原本均匀的网格，扭曲为图3(b)仿真出的形状；由于径向的放大倍率变化很大(畸变很大)，原本为圆形的标记点变成了椭圆形。从图9(b)可以看出，完成畸变校正之后，扭曲的标记点网格又变为均匀网格，并且标记点形状恢复为圆形。对比标记点的真实坐标与校正之后的坐标，相对残差如图10所示，相对残差<0.2%，可以满足高精度非球面检测加工的要求，非球面的检测结果如图11所示。

图10 畸变校正的相对残差 Fig.10 Relative residual of distortion correction

图11 非球面检测结果 Fig.11 Testing result of asphere

5 结 论

针对一大偏离度高偶次非球面，首先完成了CGH的设计；该设计通过将CGH置于干涉仪焦点内侧，在明显缩短干涉腔长度的同时，实现了对CGH多余衍射级次的分离，从而避免了衍射鬼像的干扰，同时保证CGH的刻线密度满足刻蚀加工的要求。然后，针对该检测方案，定量分析了CGH的成像畸变及畸变对像差分析的影响；分析结果表明，不同径向位置的成像倍率偏差(畸变)最大达到了2.7∶1，并且由于畸变的存在，低阶像差衍生出了明显的高阶像差。最后，通过将光线追迹与最小二乘法相结合，给出了成像畸变的校正方法，并通过实验验证了此方法的准确性。实验结果表明，校正之后的残差小于0.2%，可以满足高精度非球面检测加工的要求。

[1] IKEZAWA H,OHMURA Y,MATSUYAMA T,etal.. A hyper-NA projection lens for ArF immersion exposure tool[J].SPIE,2006,6154:615421.

[3] ROSTALSKI H J,DODOC A,ULRICH W,etal.. Projection optical system:US,0258152 A1[P]. 2007-11-08.

[4] DODOC A. High-NA projection objective:US,7848016 B2[P]. 2010-12-07.

[5] 师途，杨甬英，张磊，等.非球面光学元件的面形检测技术[J].中国光学，2014，7(1):26-46. SHI T,YANG Y Y,ZHANG L,etal.. Surface testing methods of aspheric optical elements[J].ChineseOptics,2014，7(1):26-46.(in Chinese)

[6] OFFNER A. A null corrector for paraboloidal mirrors[J].AppliedOptics,1963,2(2):153-155.

[7] KIM Y S,KIM B Y,LEE Y W. Design of null lenses for testing of elliptical surfaces[J].AppliedOptics,2001,40(19):3215-3219.

[8] WYANT J C,BENNETT V P. Using computer generated holograms to test aspheric wavefronts[J].AppliedOptics,1972,11(12):2833-2839.

[9] BURGE J. A null test for null correctors-error analysis[J].QualityandReliabilityforOpticalSystems,1993,1993:86-97.

[10] 李锐钢,郑立功,薛栋林,等.大口径高次、离轴非球面干涉测量中投影畸变的标定方法[J].光学 精密工程，2006，14(4): 533-538. LI R G,ZHENG L G,XUE D L,etal.. Calibration method for projection distortion in interferometric testing high order and off-axis aspheric surface with big aperture[J].Opt.PrecisionEng.,2006,14(4):533-538.(in Chinese)

[11] ZHAO C Y,BURGE J. Orthonormal vector polynomials in a unit circle, application: fitting mapping distortions in a null test[J].SPIE,2009,7426:74260V1-74260V8.

[12] NOVAK M,ZHAO C Y,BURGE J. Distortion mapping correction in aspheric null testing[J].SPIE,2008,7063:7063131-7063138.

[13] 王会峰.一种成像测量图像径向几何畸变的校正方法[J].应用光学，2010,31(1):55-59. WANG H F. Radial geometrical distortion correction in imaging measurement system[J].J.AppliedOptics,2010,31(1):55-59.(in Chinese)

[14] 高松涛,王高文,张健,等.用计算全息图校正非球面的畸变[J].光学 精密工程,2013,21(8):1929-1935. GAO S T,WANG G W,ZHANG J,etal.. The distortion correction of asphere testing with computer-generated hologram[J].Opt.PrecisionEng.,2013,21(8):1929-1935.(in Chinese)

[15] 高松涛,隋永新,杨怀江.用计算全息图对非球面的高精度检测与误差评估[J].光学学报,2013,33(6):0612003. GAO S T,SUI Y X,YANG H J. High precise testing of asphere with computer-generated hologram and error evaluation[J].ActaOpticaSinica,2013,33(6):0612003.(in Chinese)

[16] XIE Y,CHEN Q,WU F. Design of twin computer-generated holograms used for testing concave conic mirrors[J].SPIE,1995,6723:67235S.

[17] QI Y J,WANG P,JIANG Y. Design of CGH wavefront generator for aspheric testing with wavefront tracing method[J].SPIE,2007,6723:672362.

[18] 许英朝，张新，周平.一种三次非旋转对称的相位板的检测系统设计[J].光学学报，2008,28(5):971-975. XU Y CH,ZHANG X,ZHOU P. Optical design for unsymmetrical aspherical cubic phase plate testing system[J].ActaOpticaSinica,2008,28(5):971-975.(in Chinese)

[19] 谢意，陈强，伍凡，等.用双计算全息图检测凹非球面[J].光学学报，28(7):1313-1317. XIE Y,CHEN Q,WU F,etal.. Concave asphereical surface testing with computer-generated holograms[J].ActaOpticaSinica,2008,28(7):1313-1317.(in Chinese)

[20] 高松涛，武东城，彭石军，等.用计算全息图检测非球面时的自补偿效应分析[J].光学学报，2015,35(11):1112002. GAO S T,WU D CH,PENG SH J,etal.. Self-compensating effect analysis in testing asphere with computer-generated hologram[J].ActaOpticaSinica,2015,35(11):1112002.(in Chinese)

[21] 黄亚，马俊，朱日宏，等.基于计算全息的光学自由曲面测量不确定度分析[J].光学学报，2015,35(11):1112007. HUANG Y,MA J,ZHU R H,etal.. Investigation of measurement uncertainty of optical freeform surface based on Compurter-Generated Hologram[J].ActaOpticaSinica,2015,35(11):1112007.(in Chinese)

Distortion correcting method when testing large-departure asphere

GAO Song-tao*, WU Dong-cheng, MIAO Er-long

(EngineeringResearchCenterofExtremePrecisionOptics,StateKeyLaboratoryofAppliedOptics,ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)

With the increase in numerical aperture, the aspheric departure is also increasing in the high-NA projection objective. It is a problem to test the large-departure asphere in nanometers in the optical metrology. For an asphere with aspheric departure exceeding 500 micrometers, firstly, we design a CGH to satisfy the demands of high precise testing and etching fabrication. Secondly, the imaging distortion and the effect of distortion on aberration are analyzed quantitatively. The analysis results show that the maximum magnification deviation is 2.7∶1 for the different radial positions, and the low order aberrations will generate high order aberrations obviously. Lastly, we propose the ray trace and least square method to correct the imaging distortion when testing large-departure asphere with CGH, and verify the precision of the method through the experiments. The results show that the relative residue is less than 0.2% after correcting, and the precision will satisfy the demands of high precise optical testing and fabrication.

computer-generated hologram;CGH;distortion;asphere testing

2017-01-13；

2017-02-24

国家科技重大专项资助项目(No.2009ZX02205) Supported by National Science and Technology Major Project of China(No.2009ZX02205)

2095-1531(2017)03-0383-08

O436.1

A

10.3788/CO.20171003.0383

高松涛(1985—)，男，河南郏县人，博士，助理研究员，主要从事高精度非球面面形检测技术方面的研究。E-mail:gaost965@126.com

*Correspondingauthor,E-mail:gaost965@126.com